新型二維SiO2結構及面內應變對其光電性質影響的第一性原理研究

劉雪婷，劉禹成，趙子昂，王丹丹*，張 勇*，馮 明*

（1. 吉林師范大學 物理學院，吉林 四平 136000；2. 吉林師范大學 功能材料物理與化學教育部重點實驗室，吉林 長春 130022）

1 引 言

二氧化硅（SiO2）由于熱穩定性和化學穩定性高、介電性能和絕緣性能優異、耐蝕性好、易制備等優點，在許多現代技術和應用中發揮著關鍵作用，比如作為集成電路中的絕緣層、金屬或金屬氧化物納米顆粒催化劑的載體、玻璃的主要組分、防腐蝕保護膜等[1-4]。一般地，SiO2以三維晶體結構或無定形結構存在，尤其是其復雜的三維網格無定形結構，不利于通過表面分析技術進一步研究其表界面結構和性能的關系[5-6]。另外，隨著技術的快速發展，比如新一代的高密度存儲器（RAM）以及場效應晶體管（MOSFET）等，都需要大幅減小SiO2層的厚度、并提高其表面平整度，因此，二維（2D）結構SiO2的研發引起了研究人員的廣泛興趣[7-8]。

自2004 年Novoselov 和Geim 等獲得單層石墨烯之后，大量的二維材料被成功制備[9-16]。受此啟發，許多SiO2納米片已被成功開發[17-19]。然而，目前主要通過模板法制備的2D SiO2存在尺寸、形狀和厚度不受控制的問題，因此需要對制備SiO2的前驅體進行研究，為獲得可控厚度和尺寸的2D SiO2提供方向。另一方面，2D SiO2的原子結構尚不清楚，據報道，2D SiO2有多種晶型，和三維SiO2一樣它的基本結構單元也是[SiO4]四面體，中心Si原子被四面體頂角處的4 個O 原子包圍，但是[SiO4]四面體以何種形式連接組成2D SiO2結構還需深入研究[20]。基于上述問題，本文受通過侵蝕MAX 相來制備MXene 的方法（例如利用HF 水溶液侵蝕Ti3AlC2，可選擇性地清除Al 原子，而留下2D Ti3C2層）啟發[21-22]，從理論層面考慮可以利用類似的方法對層狀前驅體CaAl2Si2O8進行化學侵蝕處理，選擇性地清除前驅體結構中的Ca 和Al 原子，最后獲得形狀和厚度規則的2D SiO2。

本文采用第一性原理計算方法，對直接通過CaAl2Si2O8獲得的2D SiO2的結構、熱力學穩定性和動力學穩定性、電子和光學性質進行研究。并且考慮到在實際應用中，2D SiO2常與其他材料通過界面物理或化學作用結合，理論上由于材料間的晶格失配，2D SiO2將受到應變的影響，因此研究應變對2D SiO2電子及光學性質的影響，對研究其潛在應用十分必要。本文將進一步研究面內應變對2D SiO2電子、光學性質的影響。

2 計算方法

第一性原理計算采用材料模擬計算軟件VASP，對2D SiO2的結構、電子和光學性質及其受應變的影響進行模擬。在構建單層2D SiO2結構時，為消除贗胞的層間相互作用，在垂直2D SiO2面方向設置厚度為1.5 nm 的真空層。在具體的計算過程中，電子間的交換關聯能采用的是廣義梯 度 近 似（Generalized gradient approximation，GGA）下的投影綴加波贗勢（Perdew?Burke?Ernzer?hof，PBE）[23-25]，O 原 子的2s22p4、Si 原 子 的3s23p2電子被作為價電子。截斷能Ecut被設置為400 eV，優化2D SiO2原胞結構時，布里淵區K 點網格設置為8×8×1，設置的能量和原子受力收斂精度分別為1×10-4eV 和0.1 eV/nm。另外，計算電子態密度時需采用更密的K 點，因此計算態密度時我們將K-point 設置為10×10×1。進行第一性原理分子動力學模擬（AIMD）計算和聲子譜計算時，采用（3×3）的2D SiO2超胞（包含72 個O 原子和36 個Si原子）。一定溫度下的AIMD 采用NVT 系綜，AIMD 計算的時間設置為10 ps，時間步長為1.0 fs，溫度控制采用Nose??Hoover 方法[26-27]。聲子譜計算采用密度泛函微擾理論（DFPT）[28-29]，并結合phonopy 程序包進行，能量和原子受力收斂精度分別提高為1×10-8eV 和0.01 eV/nm。

對2D SiO2施加面內雙軸應變是通過改變面內晶格參數實現的。本征晶格參數為a0=b0，改變后的晶格參數為a=b，那么對2D SiO2施加的應變δ=（a-a0）/a0，δ> 0 表示拉伸應變，δ< 0 表示壓縮應變。

3 結果與討論

3.1 2D SiO2的結構

本文直接從層狀前驅體CaAl2Si2O8的結構（圖1（a）、（b））出發，刪除結構中的Ca 和Al 原子，得到2D SiO2的晶格結構（圖1（c）、（d））。結構優化計算發現，2D SiO2的結構由兩個[SiO4]四面體層以共用O 頂端的形式構成（如圖1（d）所示），具有P?62m對稱性（空間群號189）。2D SiO2的晶格參數為a0=b0=0.511 9 nm，沿c方向（圖1（d）中的真空層方向）的Si—O 鍵長為0.162 5 nm，其他的Si—O 鍵長為0.162 3 nm。另外，計算得到的2D SiO2厚度為0.435 nm，幾乎與實驗值一致[19,30]。

圖1 前驅體CaAl2Si2O8原胞結構的側視圖（a）和俯視圖（b）；2D SiO2晶格原胞結構的俯視圖（c）和側視圖（d）；（e）在800 K 溫度下2D SiO2的AIMD 結束時的結構俯視和側視圖。圖中綠色、紅色和黃色球分別代表Ca/Al 原子、O 原子和Si原子。Fig.1 Side view（a）and top view（b）of CaAl2Si2O8unit cell. Top view（c）and side view（d）of 2D SiO2unit cell. （e）Top and side views of 2D SiO2structure at the end of AIMD calculation under 800 K. The green，red and yellow balls denote Ga/Al，O and Si atoms，respectively.

為了判斷2D SiO2的機械穩定性，本文計算了其彈性模量，若2D 材料彈性模量的分量同時滿足：C11C22-C212>0 和C66>0，則2D 材料具有良好的機械穩定性。我們計算得到的2D SiO2的彈性模 量 分 量C11=C22=65.597 2 GPa，C12=C21=15.908 3 GPa，C66=8.334 9 GPa，滿 足 上 述 機 械穩定性判據，證明2D SiO2具有好的機械穩定性。

為判斷2D SiO2的熱力學穩定性，我們首先根據材料結合能的定義計算了其結合能:Ecoh（2D SiO2）=（mEO+nESi-ESiO2）（/m+n），其 中EO、ESi和ESiO2分別是每個O 原子、Si 原子和2D SiO2元胞結構的能量，m和n分別為元胞中O 原子和Si 原子的個數。計算得到2D SiO2的結合能為3.09 eV/aotm，這個值接近于實驗上已經獲得的鍺烯和硅烯的結合能（分別為3.98eV/atom 和3.72 eV/atom）[31-32]，這意味著本文預測的2D SiO2很有可能通過實驗制備獲得。另外，通過AIMD 分別模擬2D SiO2在300 K 和800 K 溫度下 的 結 構 變 化，發現在300 K 溫 度下10 ps 的AIMD 結束時2D SiO2幾乎保持了其初始結構不變，而在800 K 的AIMD結束時其結構發生了輕微扭曲（圖1（e））。這意味著2D SiO2具有良好的熱穩定性，其結構轉變溫度在800 K 以上。

隨后，利用密度泛函微擾理論（DFPT）計算2D SiO2的聲子譜來判斷其結構動力學穩定性，計算得到的聲子譜如圖2（a）所示。從圖中可看出，在整個布里淵區，晶格振動的聲子沒有虛頻（所有的頻率都大于0），這是晶格結構動力學穩定的條件[33]，說明2D SiO2具有好的動力學穩定性。

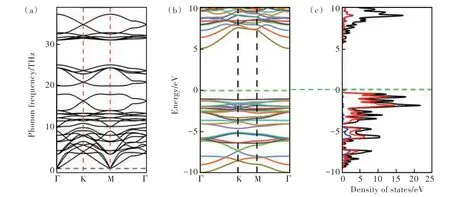
圖2 2D SiO2的聲子譜（a）、電子能帶結構（b）和態密度曲線（c）。圖（c）中黑色曲線為TDOS，紅色和藍色曲線分別為O 和Si 原子的PDOS。Fig.2 Phonon spectra（a），band structure（b）and density of state plots（c）of 2D SiO2. In （c），the black curve denotes the TDOS of 2D SiO2，the red and the blue curves respectively represent PDOS of O and Si atoms.

3.2 2D SiO2的電子和光學性質

圖2（b）、（c）為2D SiO2的電子能帶結構和電子總態密度（TDOS）及分波態密度（PDOS）。圖2（b）顯示2D SiO2的價帶頂和導帶底均位于Γ 點，且價帶頂的能帶色散曲線非常平，對應的TDOS在價帶頂處出現尖銳的峰；而導帶底的能帶色散曲線比較陡峭，對應的TDOS 在導帶底沒有出現尖銳的峰。并且從帶邊能帶色散曲線還可以看出，2D SiO2的空穴有效質量比電子有效質量更大，實際上我們結合VASP 和vaspkit 計算得到的電子和空穴的有效質量分別為0.569m0和3.749m0，這意味著電子遷移率比空穴遷移率大。經計算得到2D SiO2的帶隙為6.08 eV，說明與三維SiO2一樣，2D SiO2仍然是絕緣體，結合其形狀規則、厚度均勻的二維結構特性，2D SiO2可作為集成電路中絕緣層的優秀備選材料。

通常用復介電函數ε（ω）來描述材料的光學特性，ε（ω）=ε1（ω）+ iε2（ω），其中ε1（ω）是介電函數的實部（Re），表示電子躍遷的共振吸收，ε2（ω）是介電函數的虛部（Im），表示物質對光的吸收。根據ε（ω），可以得到材料的光吸收率、反射率、透射率以及光電導率。圖3 給出了2D SiO2的復介電函數、光吸收率、反射率、透射率和光電導率與光子能量的關系。

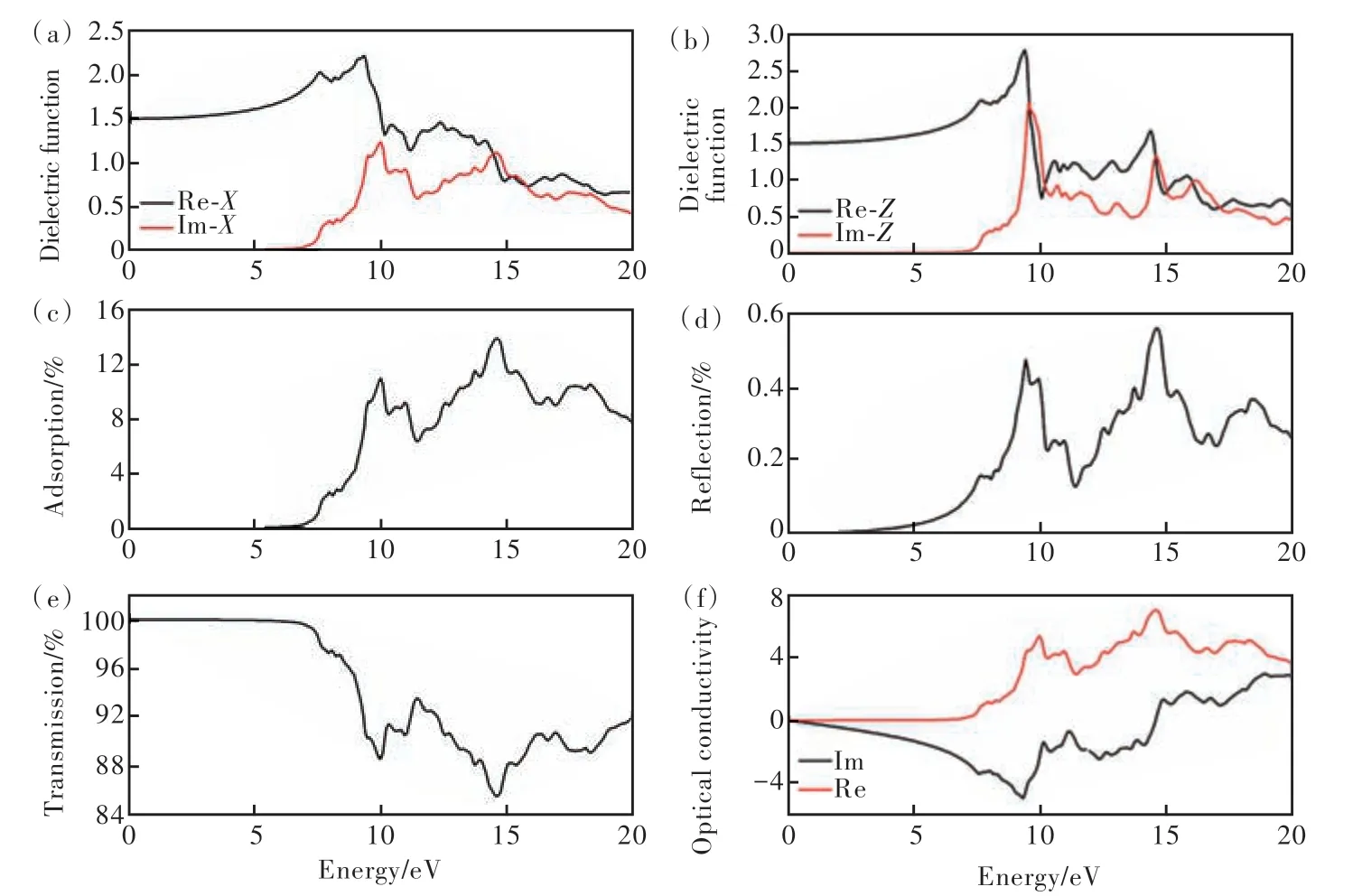
圖3 2D SiO2的x和y方向復介電函數（a）、z方向復介電函數（b）、光吸收率（c）、反射率（d）、透射率（e）、光導率（f）與光子能量的關系。Fig.3 Dielectric function inxandydirection（a），dielectric function inzdirection（b），light absorptivity（c），reflectivity（d），transmissivity（e）and optical conductivity（f）of 2D SiO2.

從圖3（a）、（b）中看出，2D SiO2的復介電函數是各向異性的，z方向與x和y方向的復介電函數不同。對于x和y方向，介電函數保持一致，靜態介電函數為ε1（0）=1.51，介電函數實部的整體變化趨勢是隨著光子能量先幾乎保持不變，然后逐漸增加，最后逐漸減小。介電函數實部ε（1ω）增加表示介質的極化程度不斷增加，ε（1ω）減小表示對電荷的束縛能力變弱。虛部ε（2ω）在0~6 eV 的光子能量范圍內為0，表示對該能量范圍的光子無吸收，這與2D SiO2的帶隙大小一致。虛 部ε2（ω）曲 線 在7.92，9.90，10.80，14.59，17.60 eV 附近出現主要峰值。對于z方向，靜態介電函數ε（10）=1.52，ε（1ω）曲線隨光子能量的變 化 關 系 與x和y方 向 類 似，但 是 在9.31 eV 處 是急劇減小的；虛部ε（2ω）在0~6 eV 的光子能量范圍內也為0，在7.99，9.53，11.60，13.0，14.70，16.20 eV 附 近 出 現 主 要 峰 值，并 且 在9.53 eV 和14.70 eV 兩處的峰比較尖銳。另外，將介電函數的虛部與能帶結構聯系，我們發現，ε（2ω）的值開始攀升的起點為其帶隙6.08 eV 對應的光子能量，并且在9 eV 左右ε2（ω）出現的很強的峰來源于高對稱K 和M 點處的電子從VBM 向CBM 的躍遷。

圖3（c）給出了2D SiO2對光的吸收率，發現2D SiO2對6 eV 以下的光無吸收，與能帶計算結果和介電函數虛部得出的結果一致。2D SiO2對光的最高吸收率發生在14.52 eV，最高吸收率為13.9%。吸收率隨光子能量變化的曲線開始攀升的起點以及峰的位置均與介電函數虛部吻合。圖3（d）為2D SiO2對光的反射率，可以看出2D SiO2對光的最大反射率僅為0.56%，說明2D SiO2對光幾乎沒有反射。圖3（e）為2D SiO2對光的透射率，2D SiO2對6.0 eV 以下光的透射率接近100%，在6~7.5 eV 范圍內對光的透射率也高達99%，隨后對大于7.5 eV 的光的透射率急劇下降，在10.0 eV 和14.5 eV 兩個位置出現光透射谷值，最小的光透射率為85.5%。上述結果說明2D SiO2是一種性能優異的透明材料，可作為二維透明涂層材料。圖3（f）為2D SiO2的光導率，光導率的實部隨光子能量變化關系與介電函數的實部和光吸收率相對應，在~7.92，9.90，10.90，14.60，17.60 eV位置出現幾個主要的峰并在14.60 eV 處達到最大值；對于光導率的虛部，在光子能量小于14.60 eV 范圍內光導率虛部小于0，在9.33 eV 處最小，然后隨著光子能量增加逐漸增加，光導率虛部的負值意味著在相應的能量范圍內2D SiO2的光電導率下降。

3.3 面內應變對2D SiO2電子和光學性質的影響

本文對2D SiO2施加的應變范圍為-5%~5%，應變梯度為1%。由于同時改變晶格參數a和b，因此施加的是雙軸應變。-5%~0 為雙軸壓縮應變，0~5%為雙軸拉伸應變。圖4 給出了2D SiO2的 帶 隙（Band gap）、價 帶 頂（VBM）和 導 帶 底（CBM）隨應變的變化關系，本文中，我們所設置的帶邊能級位置的參考能級是統一的。從圖4（a）看出，在-5%～0 的雙軸壓縮應變下，2D SiO2的帶隙隨著應變增加線性增大，在應變為-5%時，帶隙增加為6.17 eV。并且CBM 和VBM 隨著壓縮應變的增加線性地向高能方向移動，說明雙軸壓縮應變對CBM 和VBM 的作用一致。在0～5%的雙軸拉伸應變下，2D SiO2的帶隙隨著應變增加線性減小，在應變為5%時，帶隙減小為5.43 eV。值得注意的是，CBM 隨著雙軸拉伸應變是線性地向低能方向移動；而VBM 隨著拉伸應變是先向低能方向移動（0～1%），然后線性向高能方向移動（1%～4%），最后向低能方向移動（4%～5%）。CBM 和VBM 隨壓縮和拉伸應變不同的變化規律，使2D SiO2的帶隙受拉伸應變的影響更大，這點從圖4（a）中也可以看出。

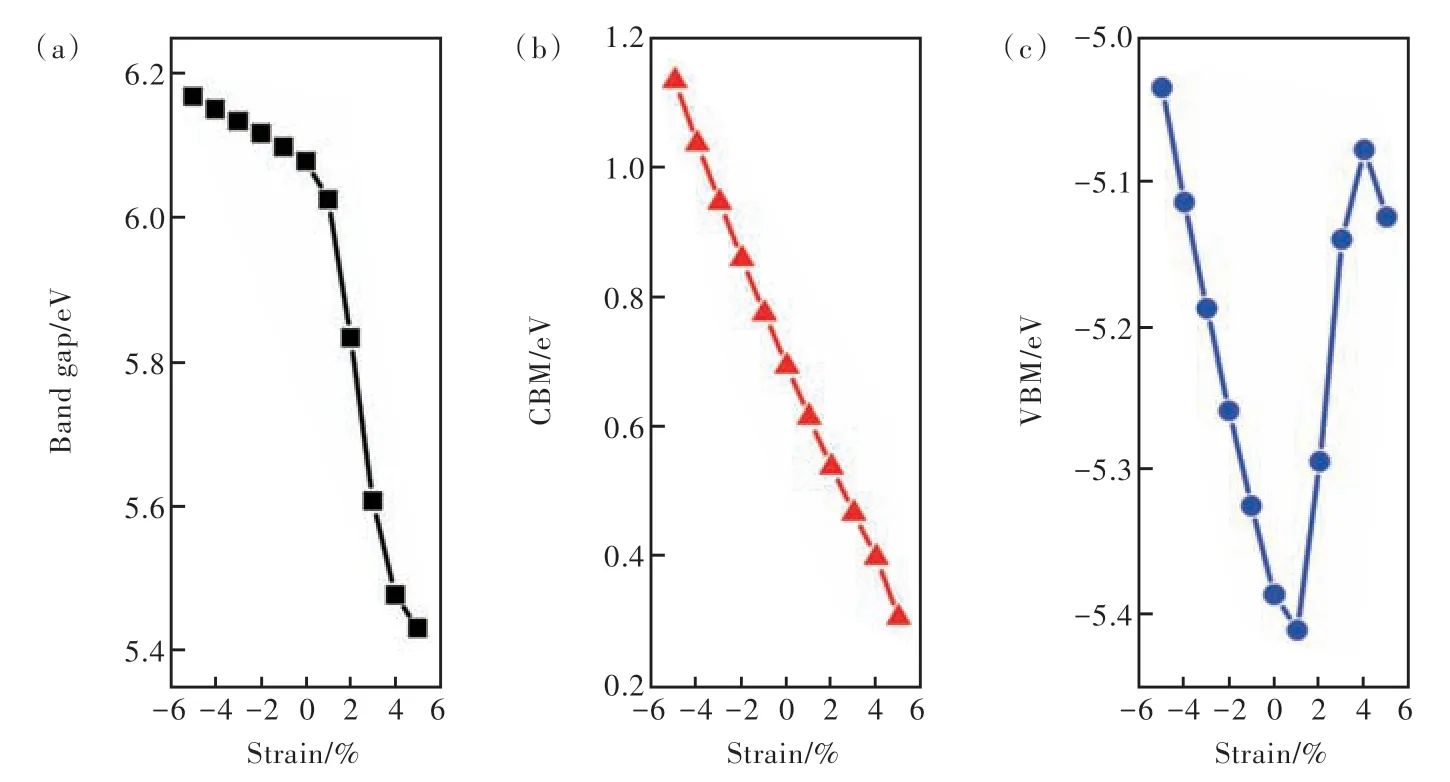
圖4 2D SiO2的帶隙（a）、導帶底（b）和價帶頂（c）隨應變的變化關系。Fig.4 The band gap（a），CBM（b）and VBM（c）values of 2D SiO2 vsstrain.

圖5 為不同的面內應變作用下2D SiO2沿不同方向的介電函數實部。x方向介電函數實部隨應變的變化規律為：在雙軸拉伸應變下，靜態介電函數ε1（0）逐漸減小，相應的0~7.5 eV 能量范圍的曲線逐漸向下輕微移動，介電函數實部的前兩個主峰位置逐漸紅移；而在壓縮應變下，靜態介電函數ε1（0）逐漸增大，相應的0~7.5 eV 能量范圍的曲線逐漸向上輕微移動，介電函數實部的前兩個主峰位置（~7.5 eV 和~9.2 eV 處）也略微紅移；從主峰位置移動大小可以看出，x方向介電函數實部受拉伸應變的影響比壓縮應變大。對于z方向介電函數實部，靜態介電函數ε1（0）隨應變的變化規律與x方向一致。不同的是，在拉伸應變下，介電函數實部的第一個主峰位置逐漸紅移，第二個主峰位置在0~3% 應變范圍內逐漸藍移、在3% ~ 5%應變范圍內紅移；而在壓縮應變下，介電函數實部的第一個主峰位置逐漸藍移，而第二個主峰位置逐漸紅移。

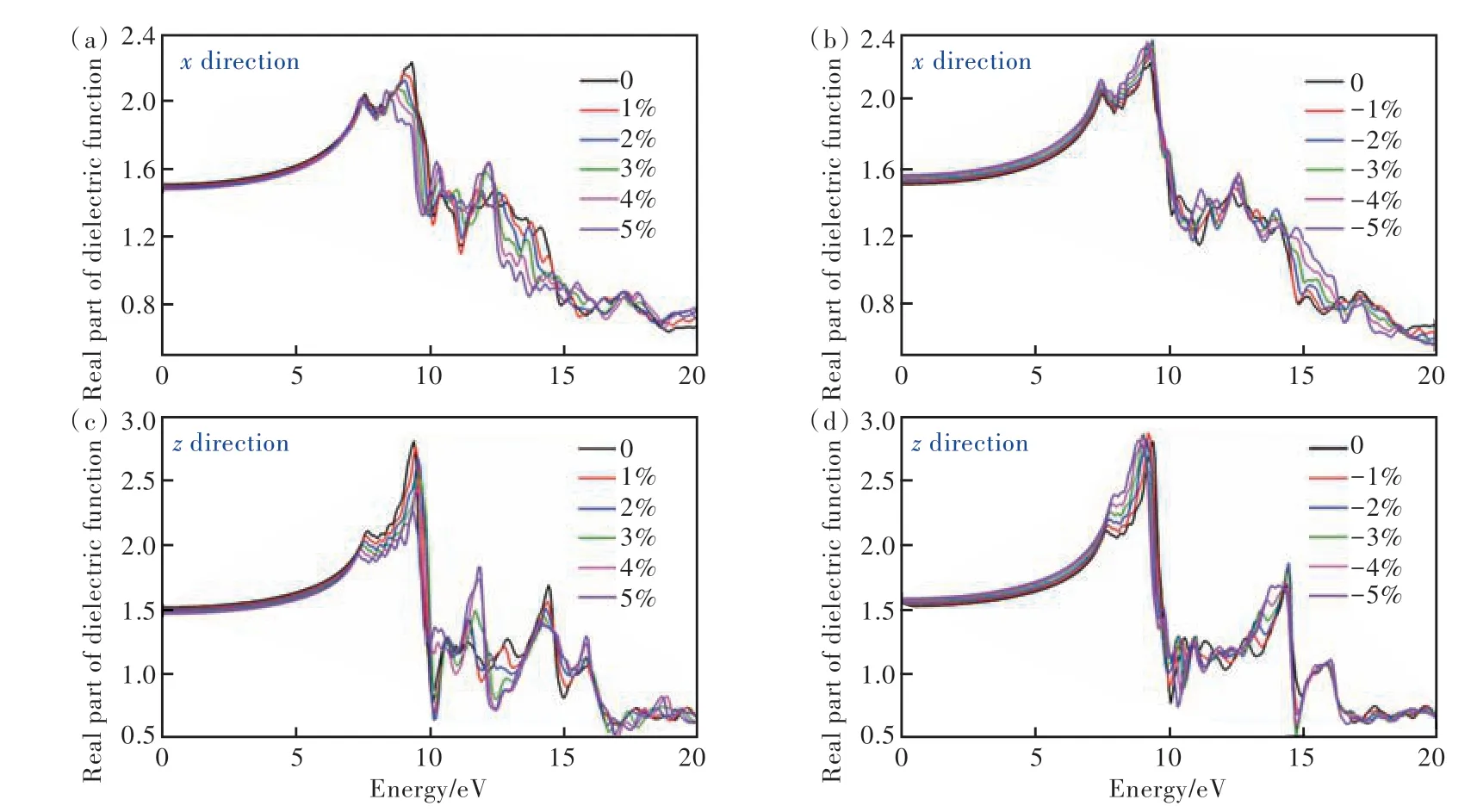
圖5 在不同應變下2D SiO2的x方向介電函數的實部：（a）拉伸應變，（b）壓縮應變；在不同應變下2D SiO2的z方向介電函數的實部：（c）拉伸應變，（d）壓縮應變。Fig.5 The real part of dielectric function ofxdirection for 2D SiO2under different strains：（a）tensile strain，（b）compressive strain. The real part of dielectric function ofzdirection for 2D SiO2under different strains：（c）tensile strain，（d）compressive strain.

圖6 為不同的面內應變作用下2D SiO2沿不同方向的介電函數虛部。從圖中看出，介電函數虛部受拉伸應變的影響比壓縮應變的大，這與電子結構（帶隙，VBM，CBM）受拉伸應變影響較大的結果一致。x方向介電函數虛部隨應變的變化為：在拉伸應變下，0~10 eV 范圍內的虛部峰逐漸紅移，且應變為5%時，在~8.7 eV 處出現新的峰，另外應變為3%~5%時在12.37 ~12.55 eV 處出現更強的新峰；在壓縮應變下，0~10 eV 范圍內的虛部峰先紅移再藍移，且應變為-5%時，在10~20 eV 范圍內出現多個新峰。z方向介電函數虛部隨應變的變化為：在拉伸應變下，~7.6 eV 處的峰逐漸紅移，~9.5 eV 處的峰在0~3%應變范圍內逐漸藍移、在3%~5%應變下逐漸紅移，并且在3%~5%應變下在~12.0 eV 處出現新的較強的峰；在壓縮應變下，~7.6 eV 處的峰逐漸藍移，~9.5 eV 處的峰逐漸紅移，且10~20 eV 范圍內的主峰都有所增強。綜合來看，在拉伸應變下，介電函數虛部曲線開始攀升的起點在拉伸應變下逐漸紅移，對應的光子能量逐漸減小，說明電子躍遷越來越容易，而曲線開始攀升的起點在壓縮應變下變化較小，說明拉伸應變會使帶邊電子的躍遷變得容易、拉伸應變對帶邊電子躍遷影響較小，這與帶隙隨應變的變化規律一致。

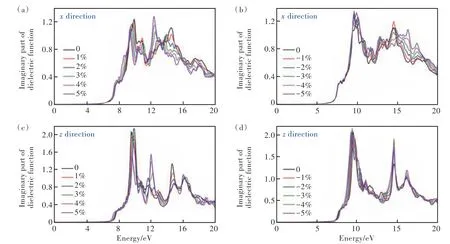
圖6 在不同應變下2D SiO2的x方向介電函數的虛部：（a）拉伸應變，（b）壓縮應變；在不同應變下2D SiO2的z方向介電函數的虛部：（c）拉伸應變，（d）壓縮應變。Fig.6 The imaginary part of dielectric function ofxdirection for 2D SiO2under different strains：（a）tensile strain，（b）compres?sive strain. The imaginary part of dielectric function ofzdirection for 2D SiO2under different strains：（c）tensile strain，（d）compressive strain.

圖7 為2D SiO2在不同應變下的吸收率、反射率、透射率和光導率。根據上述介電函數受應變影響分析，在-5%～5%范圍內的面內應變對介電函數影響不是特別大，因此為使圖片簡潔，圖7 中只給出了2D SiO2的光學性質在-5%、0 和5%應變下的曲線。從圖7（a）~（d）可看出，吸收率隨應變的變化規律與介電函數虛部的變化規律一致，拉伸應變會略微增強吸收，然而應變對整體光的吸收、反射、透射和光導率影響很小。這說明，在實際應用中2D SiO2即使在應變作用下，其光學性能依然能保持穩定，不會對器件或設備性質造成不良影響。

圖7 在不同應變下2D SiO2的吸收率（a）、反射率（b）、透射率（c）和光導率（d）。Fig.7 The light absorptivity（a），reflectivity（b），transmissivity（c）and optical conductivity（d）of 2D SiO2under different strains.

4 結 論

本文從前驅體CaAl2Si2O8出發，直接刪除層狀前驅體結構中的Ca 和Al 原子，獲得了層狀2D SiO2結構（P?62m對稱性，空間群號189）。采用第一性原理計算研究了新型2D SiO2的結合能、彈性系數、聲子譜以及分子動力學模擬，驗證了該2D SiO2結構具有良好的機械穩定性、動力學穩定性和熱力學穩定性。通過計算得到了2D SiO2的電子能帶結構、介電函數，以此獲得了其光吸收率、反射率、透射率和光導率等光學性質，發現2D SiO2是帶隙為6.08 eV 的優秀絕緣體，并且對0~7.5 eV 范圍的光透射率可達99%以上，是一種優秀的透明材料，可作為透明涂層或填充材料。另外，計算發現，在-5%~5%應變范圍內，2D SiO2的介電函數會受到影響，但是不會影響其整體光學性質，說明2D SiO2在應變作用下光學性質非常穩定。

本文專家審稿意見及作者回復內容的下載地址：http://cjl. lightpublishing. cn/thesisDetails#10.37188/CJL.20230072.