換熱器疲勞分析方法研究

李海勝，葉 奇

（中國核電工程有限公司，北京 100840）

0 引言

換熱器是核電廠熱量交換關鍵部件，屬于管殼式換熱器。因其承載溫度瞬態多變、溫差大，該結構的疲勞分析是其安全性評定的主要方式之一[1-3]。換熱器整體疲勞分析對計算硬件要求高，通常采用三維簡化模型進行計算分析[4]。換熱器局部模型疲勞分析可對局部瞬態計算以及進一步疲勞分析提供依據。

本文研究了某核級換熱器局部區域在熱載荷和內壓載荷下的疲勞分析結果，采用ANSYS 有限元軟件建立二維對稱模型，根據RCC-M 規范[5]要求，分別對疲勞使用因子、一次加二次應力范圍以及熱棘輪效應進行分析，并研究了溫度變化率和溫度變化范圍對計算結果的影響。

1 計算模型及加載方式

1.1 計算模型

換熱器局部二維計算模型主要包括管程出口接管和封頭，有限元計算模型如圖1 所示。計算分析對計算模型敏感區域設置路徑并提取對應結果，路徑設置和路徑位置編號如圖1 所示。設備材料為Z2CN1810，不同溫度下材料參數（基本許用應力強度Sm、屈服強度Sy、抗拉強度ee、導熱率λ、熱膨脹系數α、彈性模量E、比熱容Cp、熱擴散率以及設計疲勞曲線數據及計算彈塑性修正系數的參數m 和n 值）根據RCC-M 規范取值。本文將對計算模型進行溫度場分析、熱應力場分析和結構應力分析。

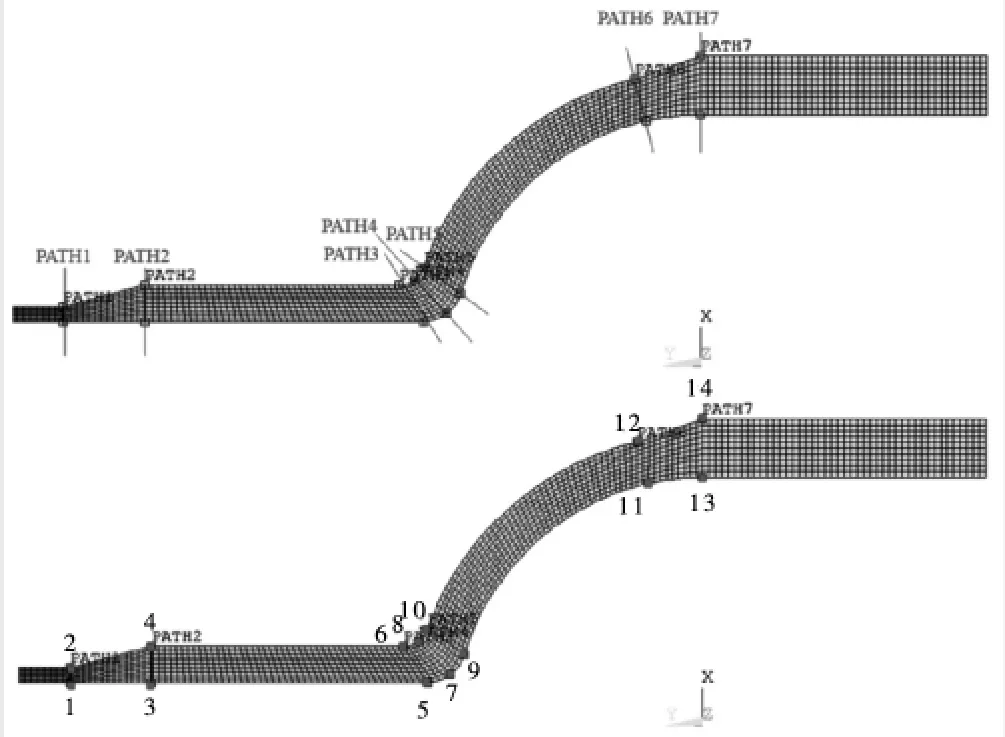
圖1 計算模型（路徑及路徑位置編號）

1.2 加載方式

換熱器疲勞分析載荷考慮了溫度瞬態和壓力載荷，其中溫度瞬態載荷的加載方式如圖2 所示。對固體邊界施加流體溫度瞬態及相應的換熱系數進行熱分析，得到溫度場隨時間的變化。之后，再將此溫度場作為輸入，進行熱應力分析及相應疲勞分析。封頭截斷面施加全自由度約束。

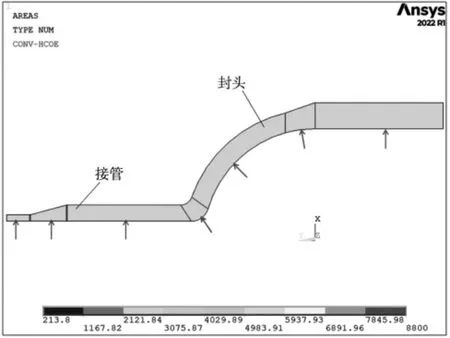
圖2 加載方式

2 計算條件

2.1 溫度瞬態

換熱器承受多個溫度瞬態工況載荷，其中一個溫度瞬態如圖3 所示，瞬態次數N=200，壓力為15.8 MPa 且保持不變。

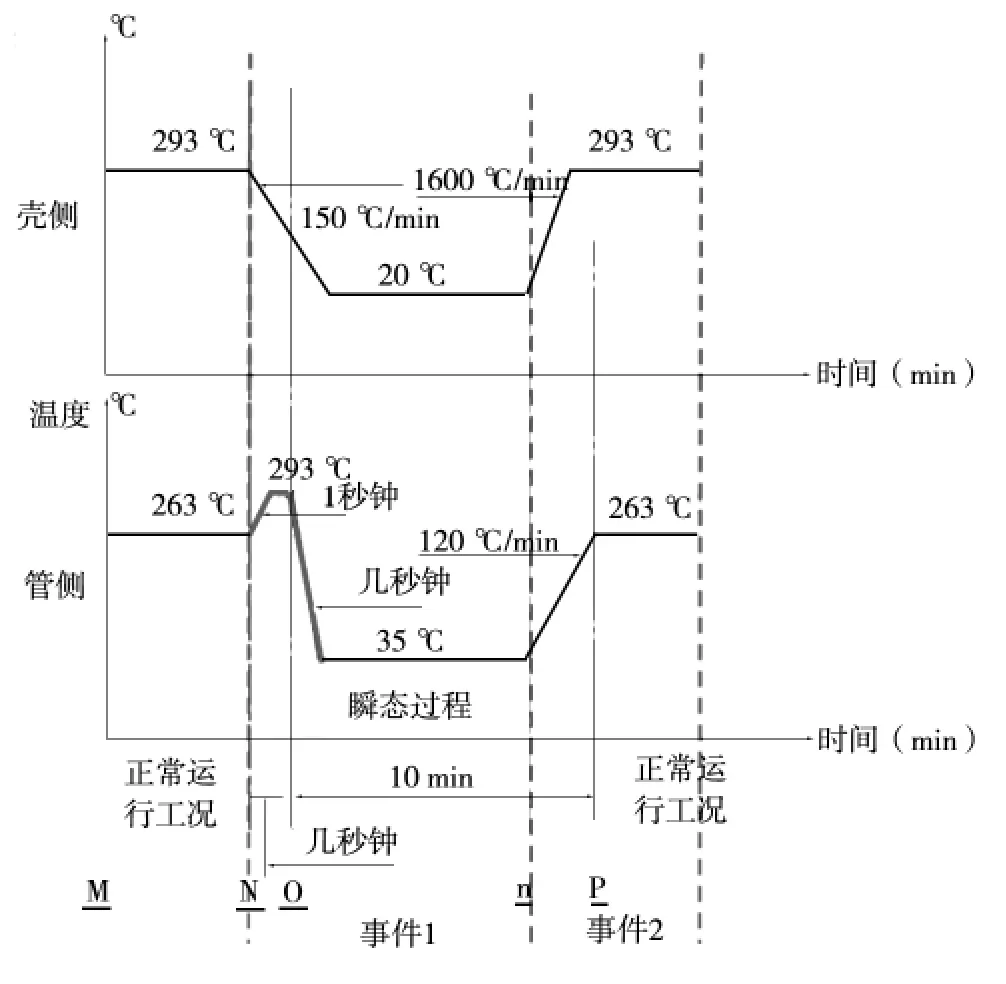
圖3 溫度瞬態

2.2 計算模式

為研究溫度變化率和溫度變化范圍的影響，根據圖3 管側溫度瞬態中“幾秒鐘”時長取值和升降溫條件，可采用以下三種模式進行計算：

（1）A 模式：按5 s 取值且293 ℃至35 ℃線性瞬變。

（2）B 模式：按2 min 取值且293 ℃至35 ℃線性瞬變。

（3）C 模式：按2 min 取值且263 ℃至35 ℃直接瞬變。

以下分別對三種不同模式進行計算分析。

2.3 事件定義

疲勞分析主要是由于結構溫度瞬態改變產生的結構應力變化引起，因而可根據溫度瞬態改變區域進行事件定義，如圖3 所示。由于溫度改變引起的結構應力變化具有滯后性，因而溫度場分析時，為使結構應力達到穩態，事件定義需延長足夠時間段[6]。

3 計算結果

3.1 疲勞使用因子

圖4 所示為熱載荷下不同計算模式的各路徑位置疲勞使用因子的計算結果。

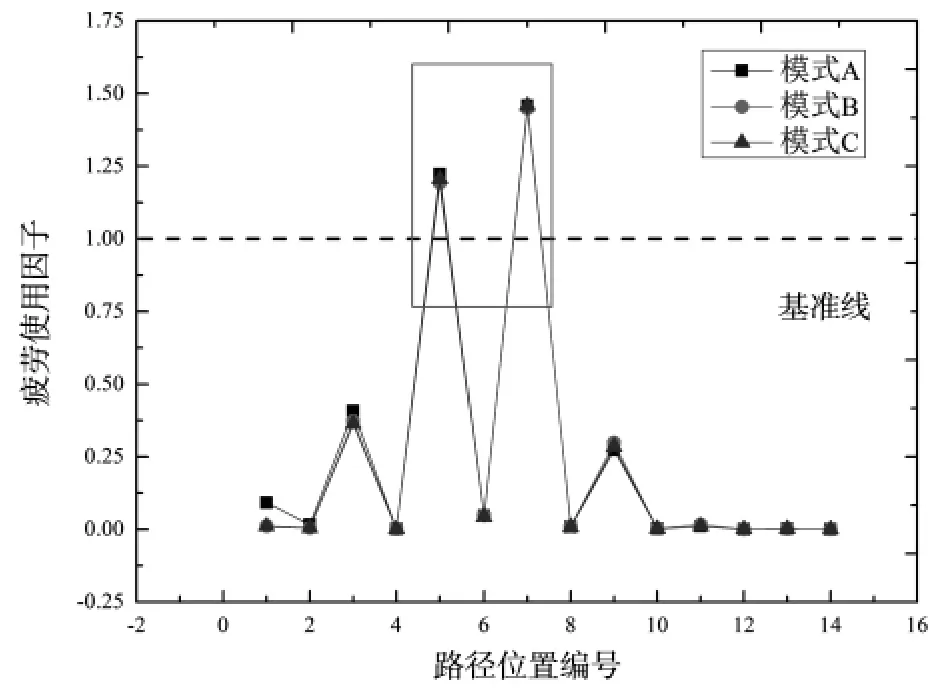
圖4 熱載荷下不同計算模式的各路徑位置疲勞使用因子

根據RCC-M C3200 規范要求，可以得出以下結論：

（1）熱載荷下不同計算模式的換熱器計算結果顯示：敏感區域的疲勞使用因子不滿足規范要求且主要位于接管與封頭連接區域。

（2）相比于計算模式B 和計算模式C，計算模式A 的計算結果更加嚴苛，即溫度變化率的增加會使得應力敏感區域的疲勞使用因子增大。

圖5 給出了熱載荷下不同計算模式的各路徑位置點的總應力變化幅值Sp以及不同模式間相對比的結果。可以得出以下結論：

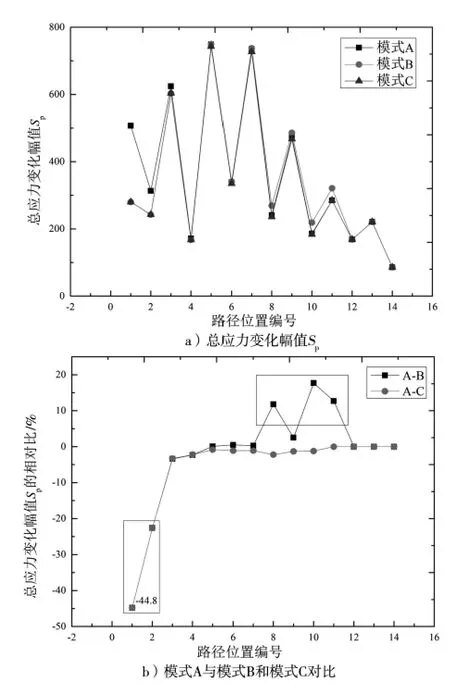
圖5 熱載荷下不同計算模式的各路徑位置

（1）管側溫度變化率和溫度變化范圍將會影響換熱器熱應力敏感區域的總應力變化幅值Sp。

（2）不同計算模式影響熱載荷下應力敏感區域，主要包括：接管薄壁段、接管與封頭連接區域。

（3）對于接管薄壁段，無論溫度變化范圍，溫度變化率的降低會降低該位置的Sp；而對于接管與封頭連接區域，溫度變化率的降低和溫度變化范圍的增加均會增加該位置的Sp。

以模式A 為例，對總應力幅值Sp進行分析。根據RCC-M C3284規范要求，即使在僅考慮熱載荷的情況下，Sp計算最值約為624.36 MPa，其大于許用值2Sa，即計算模型的應力Sp不滿足規范要求。參考圖5、圖6，模式B 和模式C 具有同樣結果。

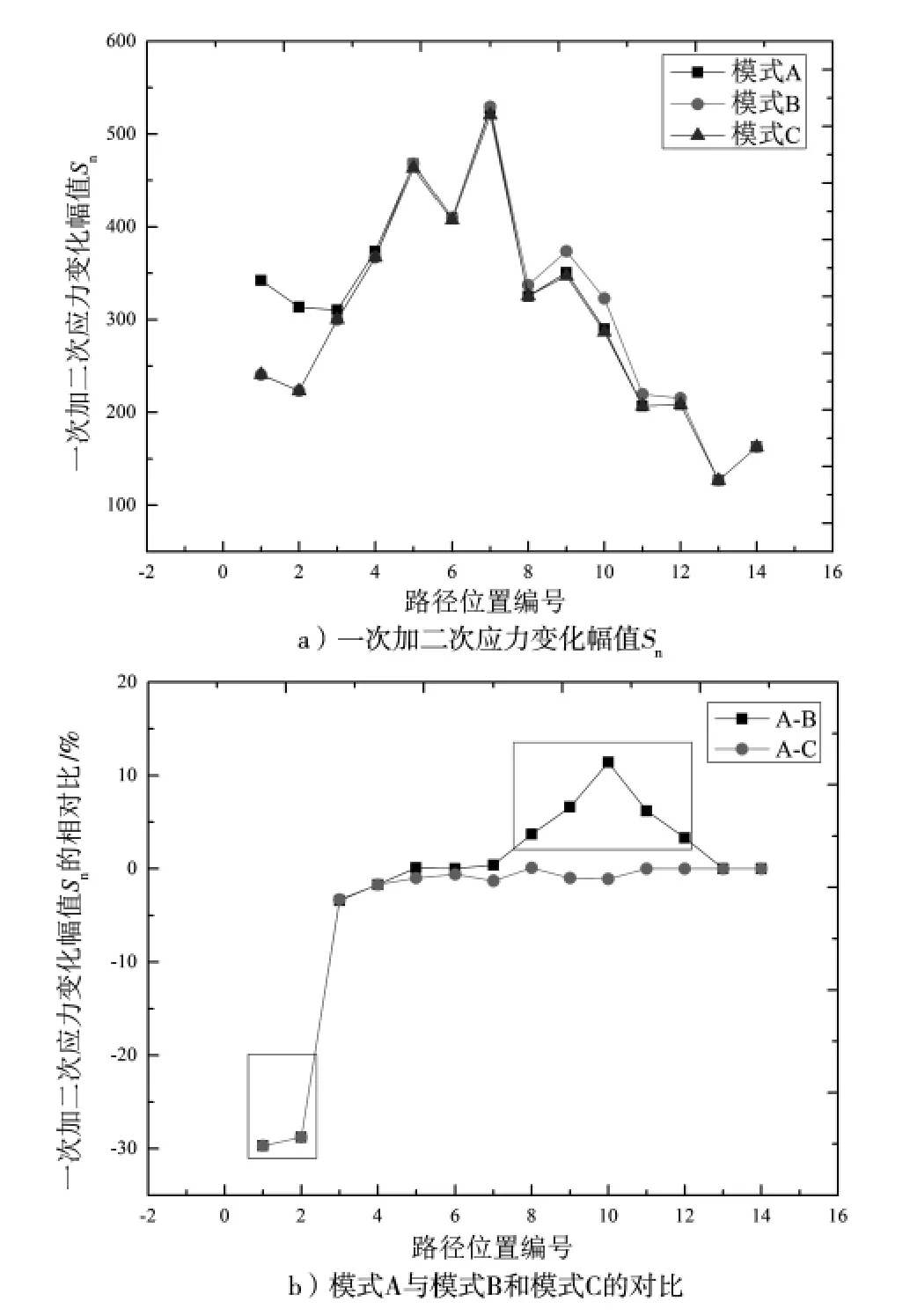
圖6 熱載荷下不同計算模式的各路徑位置

3.2 一次加二次應力范圍評定

圖6 給出了熱載荷下不同計算模式的各路徑位置點的一次加二次應力變化幅值Sn以及不同模式間對比的結果。可以得出與溫度變化率和溫度變化范圍對Sp的影響具有相同趨勢的結論。

同樣，換熱器計算模型的一次加二次應力評定以模式A 為例。根據RCC-M C3284 規范要求，即使在僅考慮熱載荷的情況下，Sn計算最值約為527.16 MPa，最值仍大于許用值3Sm，即計算模型的應力Sn同樣不滿足規范要求。參考圖5、圖6，模式B和模式C 具有同樣結果。

3.3 熱棘輪效應分析

因換熱器計算模型承受恒定內壓和循環溫度變化載荷，可能會由于熱棘輪效應而發生漸進性大變形。因此，根據RCC-MC 3284.7 規范要求，對計算模型進行熱棘輪效應分析。

換熱器計算模型為承受恒定內壓的軸對稱旋轉殼體，為避免殼體直徑逐次增加，計算模型殼體所允許的最大循環熱應力極限值σθ由式（1）確定：

其中，Sy為規范列出的在循環過程中最高溫度下的屈服極限（若1.5Sm＞Sy，則可采用1.5Sm），即Sy=max（Sy，1.5Sm）；y′值根據計算x 值進行判斷取值。

經計算，293 ℃下，屈服極限Sy=max（108.7，）=146.55 MPa；內壓引起的總體薄膜應力最值為36.0 MPa。根據式（1）計算，x值約為0.246。

（1）假設溫度沿壁厚線性分布，則y′值根據式（2）進行取值：

根據式（2）計算得出y′=4.066；根據式（1）計算得出熱應力變化范圍最大許用值σθ約為595.86 MPa；Sn計算最值527.16 MPa。因而，可根據Sn＜σθ，假設溫度沿壁厚線性分布，則滿足規范要求。

（2）假設溫度沿壁厚拋物線分布，則y′值根據式（3）進行取值：

根據式（3）計算得出y′=4.65；根據式（1）計算得出熱應力變化范圍最大許用值σθ約為681.46 MPa。因而，可根據Sn＜σθ，假設溫度沿壁厚拋物線分布，則滿足規范要求。

4 結論

本文通過建立某核級換熱器二維對稱模型，對其關鍵應力敏感區域進行疲勞分析，選取合適路徑，對其疲勞使用因子、一次加二次應力和熱棘輪效應分別進行分析，并對管側溫度變化率和溫度變化范圍的影響進行計算分析。計算結果表明：

（1）換熱器疲勞易損區域主要集中于接管與封頭連接區域。

（2）管側溫度變化率和溫度變化范圍均對應力敏感區域的一次加二次應力變化幅值Sn和總應力變化幅值Sp產生顯著影響，偏差最值可達44.8 %。

（3）沿壁厚溫度分布規律對熱棘輪效應分析結果具有直接影響。

以上結論是基于二維對稱模型進行計算分析得到的，計算方法和結果具有較大的保守性，對危險區域應考慮開展更詳細的疲勞分析。