水下振蕩渦流場聲散射與調制特性

荊晨軒, 時勝國1,2,, 楊德森1,2,

(1.哈爾濱工程大學 水聲技術重點實驗室,黑龍江 哈爾濱 150001; 2.海洋信息獲取與安全工業和信息化部重點實驗室(哈爾濱工程大學),工業和信息化部,黑龍江 哈爾濱 150001; 3.哈爾濱工程大學 水聲工程學院,黑龍江 哈爾濱 150001)

聲波在渦流場傳播時,渦流場與聲波會發生流聲耦合作用,產生聲散射現象[1-2]。回轉體在繞流場中會產生交替脫落的卡門渦街,可演化出具有周期性結構的振蕩尾渦,在自然界和實際工程中廣泛存在[3-5]。研究水下振蕩渦流與聲波的耦合作用規律,對結構物尾流識別及探測、認識復雜流場與聲波相互作用有著重要意義,具有工程應用與科研價值。二維渦旋聲散射問題是聲波在復雜流場中傳播的基本問題,在水聲學、氣動聲學中都有廣泛應用[6-8]。Colonius等[9]基于線性納維斯托克斯方程(linear navier Stokes, LNS),選取了多個基本渦流結構,采用直接數值模擬(direct numerical simulation, DNS)開展了聲散射研究,并為驗證模型算例提供了數值參考。Cheinet[10]基于線性歐拉方程(linear Euler equation, LEE),采用二階中心時域有限差分(finite difference time domain, FDTD)格式數值計算了聲波穿過渦流場的散射情況,為研究大氣湍流對聲傳播的影響提供了一種數值方法。Ke等[11]采用高階加權本質無振蕩(weight edessentially non-oscillatory, WENO)格式數值計算了聲波穿過多種渦結構的散射情況,獲得的結果與Colonius采用直接數值模擬的計算結果相吻合。Clair[12]通過建立平面波渦流散射的半解析模型及時域有限差分格式數值求解了線性歐拉方程,研究了運動渦對散射聲場的影響特性。文獻[13-14]通過線性緊致格式直接數值求解二維歐拉方程,獲得了聲波穿過均熵渦流的散射特性,并分析了無量綱尺度量渦強度和長度尺度比對散射聲場的影響。流聲耦合研究主要集中在氣動聲學領域,在水下流場聲散射研究方面,張詠鷗等[15]基于攝動聲學理論建立流聲耦合作用下的聲散射模型,采用時域有限差分格式進行數值求解,對水下渦流場前向聲散射特性進行了分析,探究了散射聲場形態函數和指向性。

本文針對經典Gaussian渦流模型,采用間斷伽遼金(discontinuous Galerkin, DG)方法數值求解了運動流場聲散射模型。在驗證數值方法有效性的基礎上,研究了水下振蕩渦流場對聲場的散射和調制作用,分析了不同馬赫數、尺度波長比和頻率比條件下振蕩渦流場對聲場的散射與調制特性。

1 流聲耦合理論模型

1.1 控制方程

為了建立水下振蕩渦流場的聲散射調制模型,從流體力學基本方程組出發[16]:

(1)

式中:ρ、u分別為流體密度、速度。假設聲學量為擾動量,聲學量級遠遠小于對應的流體變量:

(2)

式中:ρ0、u0、p0分別為不考慮聲擾動的流場密度、速度矢量和壓力,ρ′、u′、p′分別為聲場對應的密度變化量、速度矢量和聲壓,代入流體力學基本方程組并略去高階小量,得到[16]:

(3)

方程(3)為水下流聲耦合作用的聲場控制方程,通過對該方程的數值求解,能夠數值模擬水下振蕩渦流場對聲波的散射和調制作用。為保證數值計算精度,本文采用DG方法[17]對控制方程進行求解,其方法結合了傳統有限元方法和有限體積方法的優點,具有精度高、耗散和色散小等特點,且良好的穩定性和收斂性,容易實現高階格式。時間步進采用四階龍格-庫塔格式。為了減少邊界反射對計算的影響,在邊界處設置聲吸收層。

1.2 渦旋模型

二維渦流聲散射問題是聲波在復雜流場中傳播的基本問題,下面針對經典Gaussian渦流模型[9]進行計算和分析:

(4)

式中:vr為徑向速度;vθ為切向速度;r為觀測點到渦核中心的距離;L為渦核尺度,切向速度在在r/L=1處達到最大;Γ∞為參數常量。物理模型如圖1所示,一個波長為λ的平面聲波在傳播過程中穿越一Gaussian渦,左右設置為吸收層,避免反射的影響,聲場計算域是邊長為10λ×10λ的正方形區域。

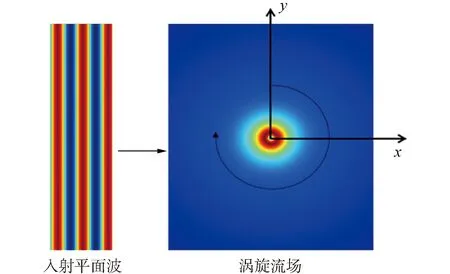
圖1 渦旋聲散射模型示意Fig.1 Schematic diagram of the physical model

1.3 模型驗證

為了考察本文方法的可行性和計算結果的準確性,選取Colonius[9]算例結果并進行對比,如圖2所示,圖2中prms為時域散射聲壓的均方根值:

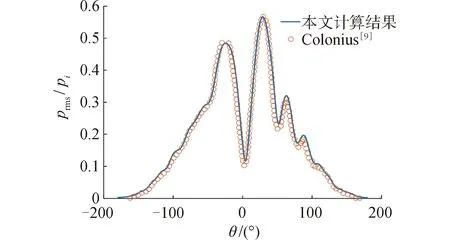
圖2 渦旋聲散射模型驗證Fig.2 Verification of vortex acoustic scattering mode

(5)

式中:ps為散射聲壓;p為總聲壓;pi為入射聲壓。由圖2可知,本文方法得到的結果與文獻中的計算結果吻合度很高,證明了本文方法的有效性。

假定Gaussian渦流速度結構產生周期性振蕩:

(6)

水聲學問題不同于空氣聲學,一般馬赫數較小,且自然流場多為長周期波,因此選取流場振蕩頻率與入射聲波頻率之比較小[18]。馬赫數Ma為0.01,入射聲波頻率f0為375 Hz,波長為λ,周期為T0,流場振蕩頻率f1為15 Hz,周期T1為25T0,流場振蕩周期T1遠大于聲場周期T0,渦流尺度L為λ/4,觀測點選取在距渦流中心2.5λ處。

在此基礎上,本文通過聲散射指向性曲線進行時間無關性和網格無關性驗證。為了避免截取信號時間長短對分析結果的影響,進行時間無關性驗證,分別選取時間長短為4T1、6T1、8T1進行求解,如圖3所示。可以看到計算時間長短達到4T1及以上時,計算得到的散射指向性具有良好的一致性,分析選取的時間長度為4T1。對應網格在一個波長范圍內分別設置12、18、24個節點求解,進行網格無關性驗證,如圖4所示。可以看到每波長網格數達到12個及以上時,計算得到的聲散射指向性曲線具有良好的一致性,為了兼顧計算量和散射聲壓云圖分辨率,下面進行分析選取的網格數為每波長18個網格。

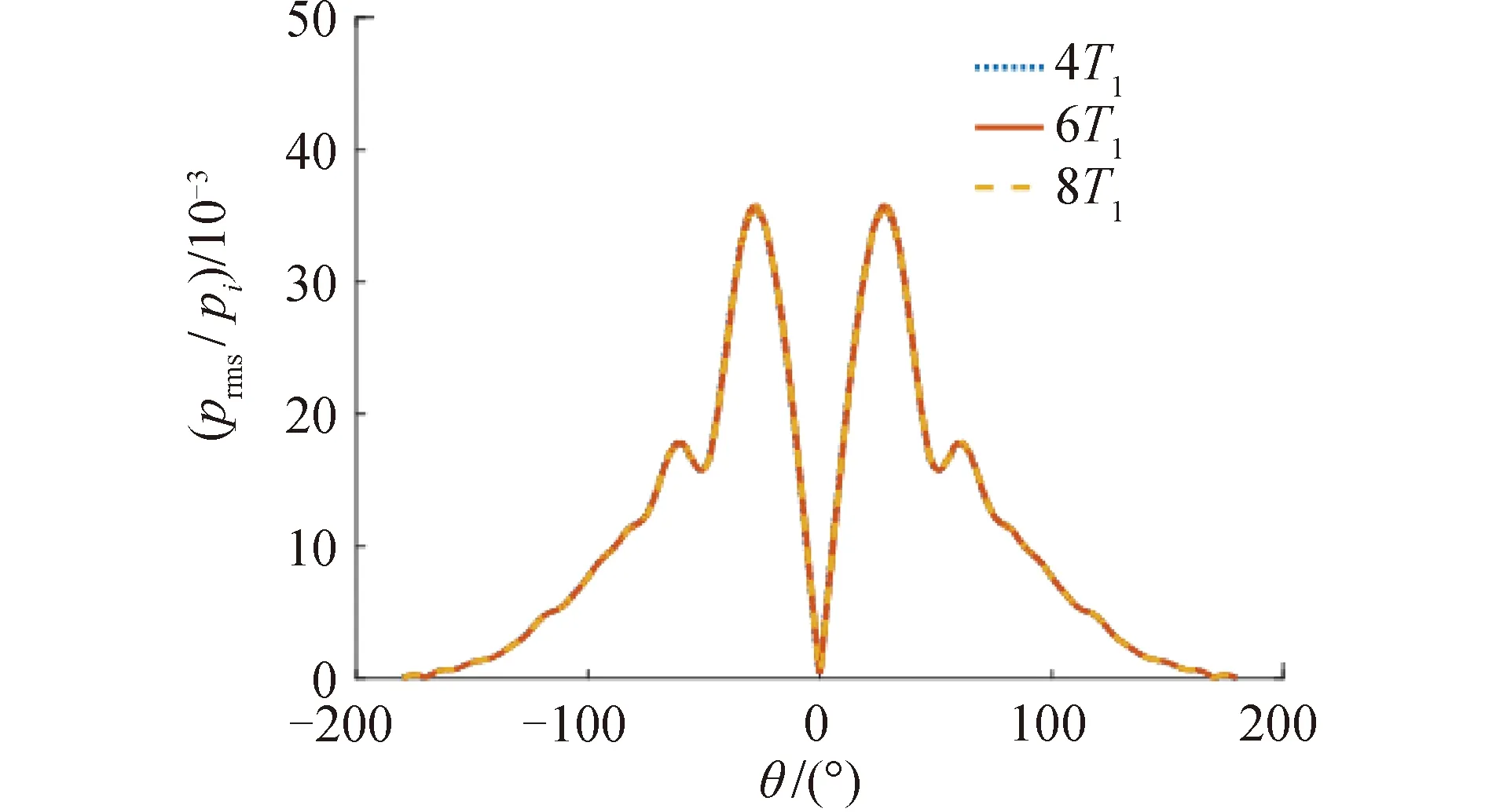
圖3 時間無關性驗證Fig.3 Time independent verification

2 數值計算結果與分析

2.1 振蕩渦流對聲場的散射和調制

根據圖3、4可知聲場最大散射方向大約處于±30°處,因此選擇方向為30°處的時域聲信號,分析渦流有無振蕩時對聲場的影響。觀測點聲壓隨時間變化曲線如圖5、6所示。通過Hilbert變換提取聲壓信號包絡,進行包絡譜分析,如圖7所示,包絡線譜與渦流振蕩頻率f1一致。對觀測點聲壓信號進行頻譜分析,如圖8所示,渦流場振蕩時聲壓信號頻率變為f0、f0±f1、f0±2f1,渦流場無振蕩時聲壓信號頻率依然為入射聲波頻率f0。可以看出聲波經過振蕩渦流場后,渦流場的振蕩頻率調制到聲波頻率上,本文將這種現象稱為流場與聲場發生調制作用,而渦流無振蕩時,不會發生調制作用。

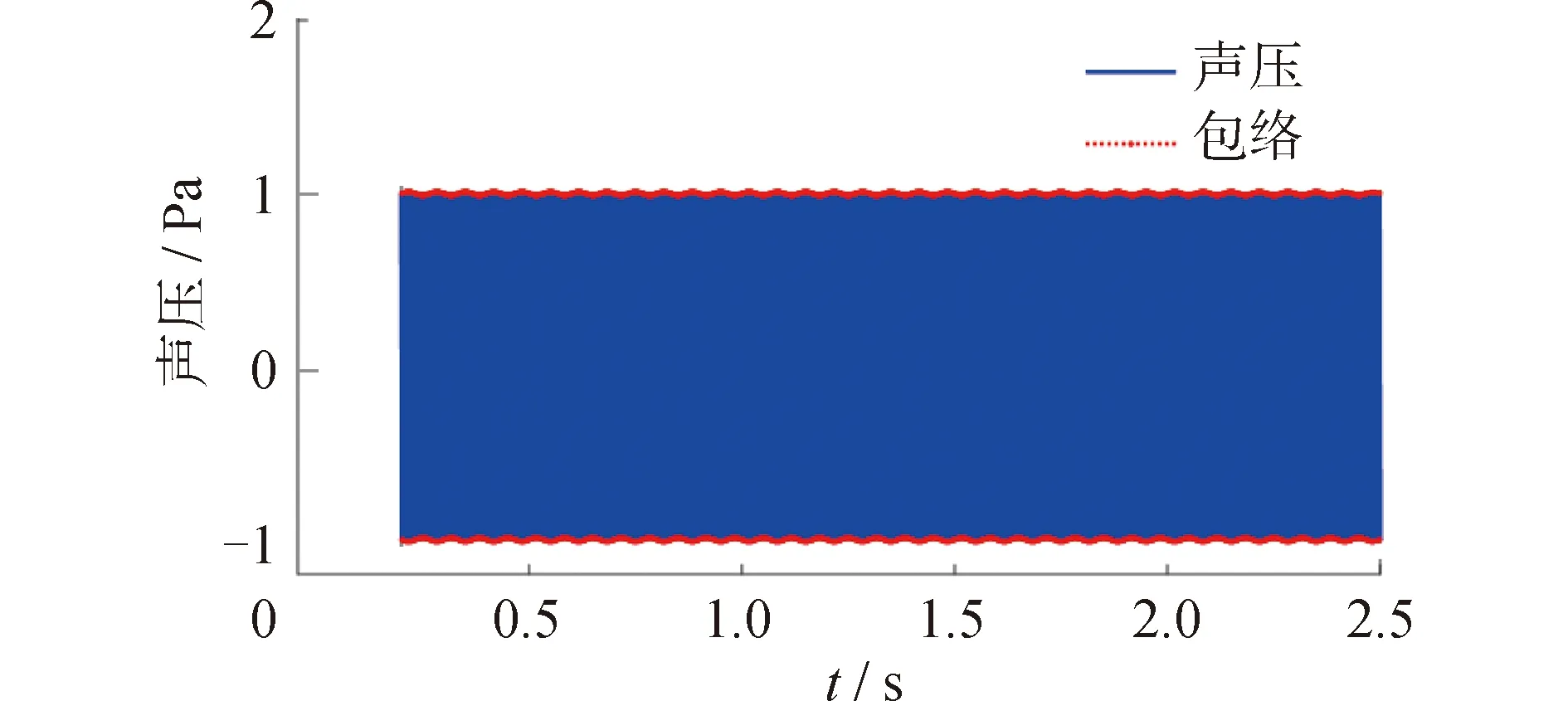
圖5 振蕩渦流場觀測點聲壓時域圖Fig.5 Time domain diagram of sound pressure at observation point of oscillating eddy current field

圖6 無振蕩渦流場觀測點聲壓時域圖Fig.6 Time domain diagram of sound pressure at observation point of non-oscillating eddy current field

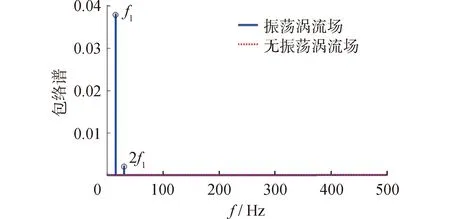
圖7 觀測點聲壓包絡譜圖Fig.7 Sound pressure envelope spectrum of observation point

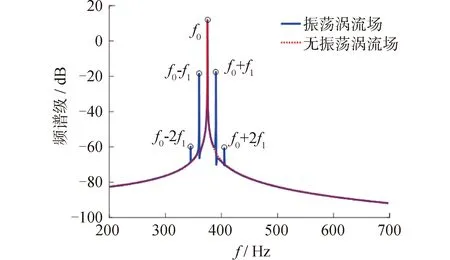
圖8 觀測點聲壓頻譜Fig.8 Spectrogram of sound pressure at observation point

渦流場振蕩時散射聲壓不同時刻云圖如圖9所示,聲波在運動流體中傳播受到流場速度和速度梯度的影響,從而產生散射聲壓[1,19],產生調制作用的主要原因是渦流場發生振蕩后,由于渦流場速度發生周期性變化,從而引的周期性變化,使得入射聲波頻率調制上渦流場的振蕩頻率。

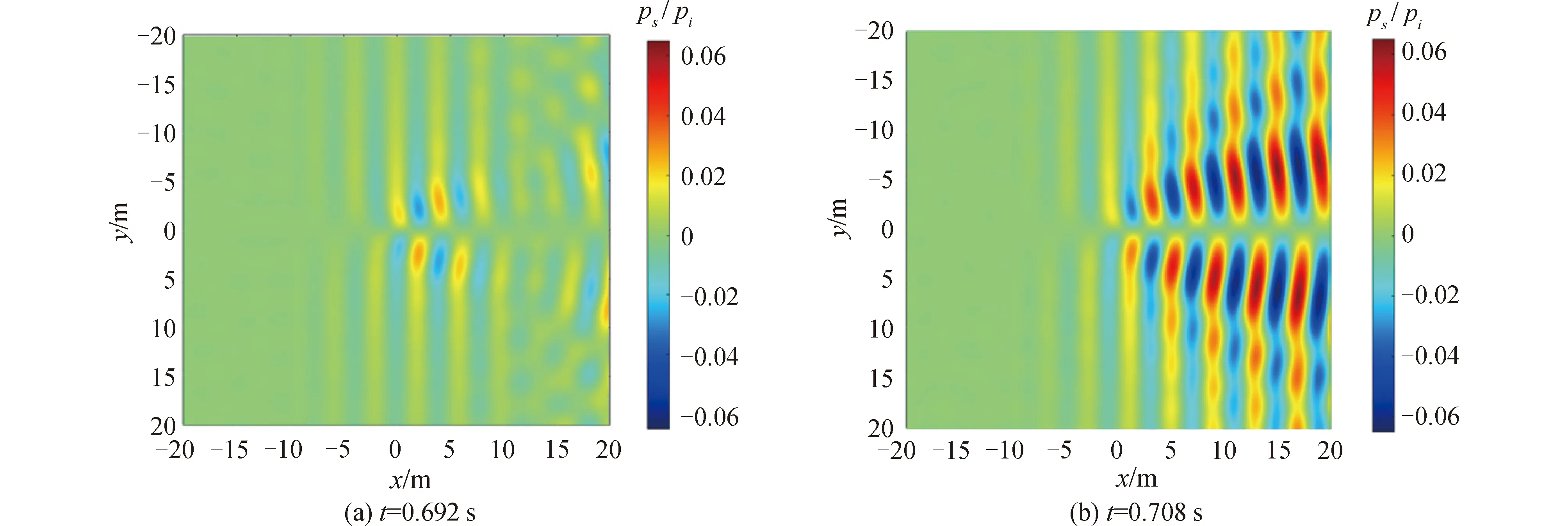
圖9 不同時刻振蕩渦流場散射聲壓云圖Fig.9 Cloud map of scattered sound pressure of oscillating eddy current field at different times

為了更為直觀地評價流聲耦合作用,分別采用散射截面和調制深度描述流場對聲場的影響程度。采用散射截面Σ描述聲場指向性及散射強度特性[13]:

(7)

式中:θ為觀測角度;r為觀測半徑。

以渦流中心為圓心, 在圓周上對散射有效聲壓與入射聲壓之比的平方進行積分,為用來衡量流場對聲波散射作用的強弱。采用調制深度m[20]描述聲場某點處的包絡特征,用來衡量渦流場對聲場的調制作用強弱,渦流場無振蕩時,聲場不存在調制深度。調制深度m為:

(8)

式中:rmax為已調制波的最大振幅;rmin為最小振幅;pmax為載波最大振幅;pmin為最小振幅。

通過改變渦流場特征分別改變馬赫數Ma、渦流尺度與聲波波長比(下面稱尺度波長比)L/λ、渦流振蕩頻率與入射聲波頻率比(下面稱頻率比)f1/f0,研究上述渦流場參數對聲場散射和調制作用的影響。

2.2 馬赫數影響分析

在低馬赫數條件下,對Ma分別為0.001 25、0.002 5、0.005、0.01、0.02時的流聲耦合問題進行計算,不同馬赫數流場聲散射指向性隨方位變化關系如圖10所示,對于所計算范圍內,隨著馬赫數增大,不同馬赫數下的聲散射指向性曲線形狀基本一致。

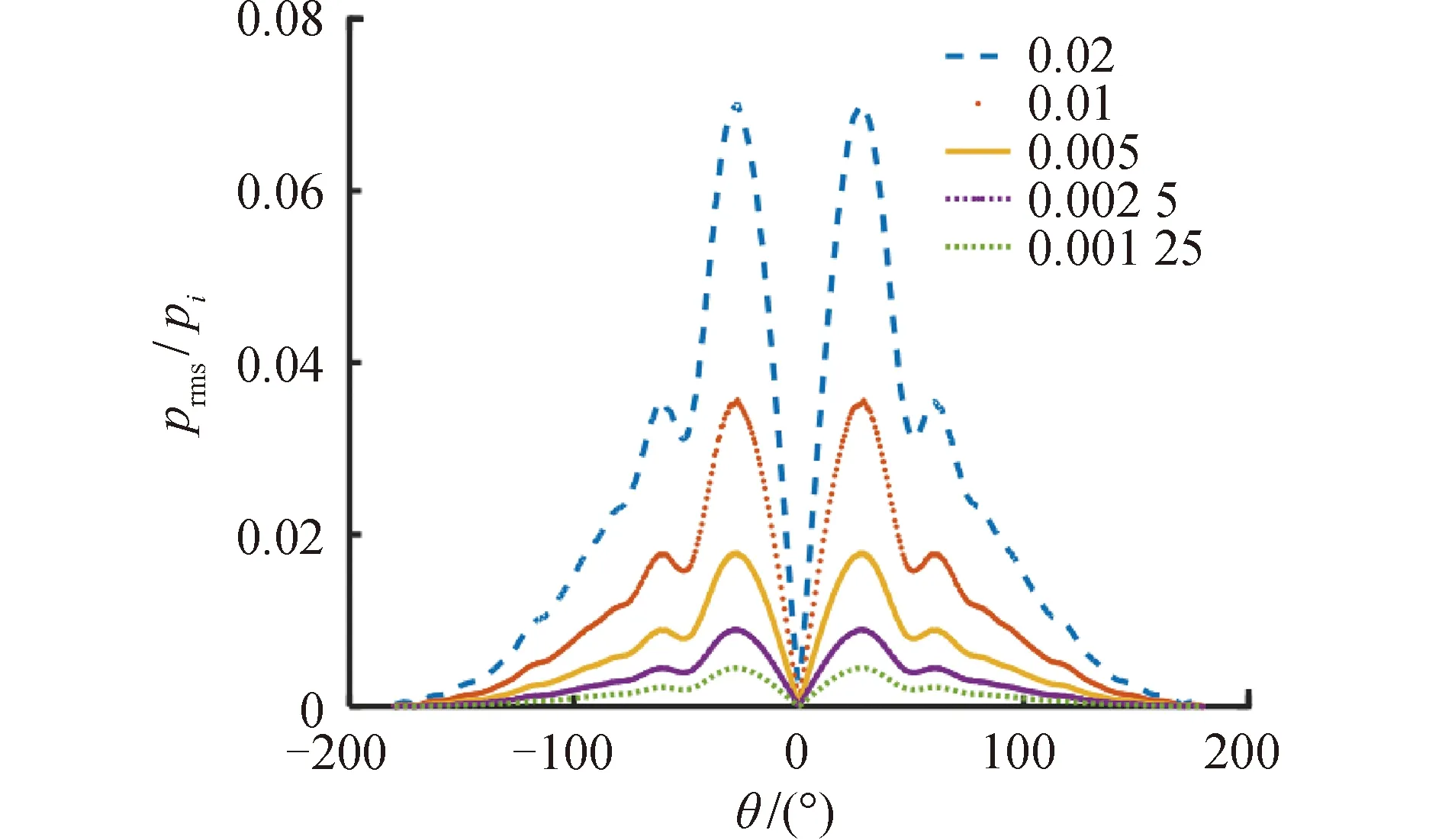
圖10 不同馬赫數聲散射指向性Fig.10 Directivity diagrams of acoustic scattering at different Mach numbers

散射截面和調制深度隨馬赫數變化規律曲線分別如圖11、12所示,可以看出在低馬赫數條件下(Ma<0.05),對于所計算的馬赫數范圍,散射截面和調制深度隨著馬赫數的增加而增加,散射截面與馬赫數具有接近平方的關系,調制深度與馬赫數具有接近正比的關系。

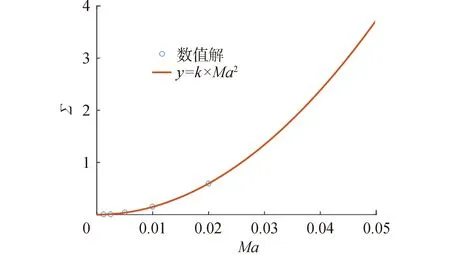
圖11 散射截面隨馬赫數變化規律Fig.11 The variations of scattering cross section with Mach number

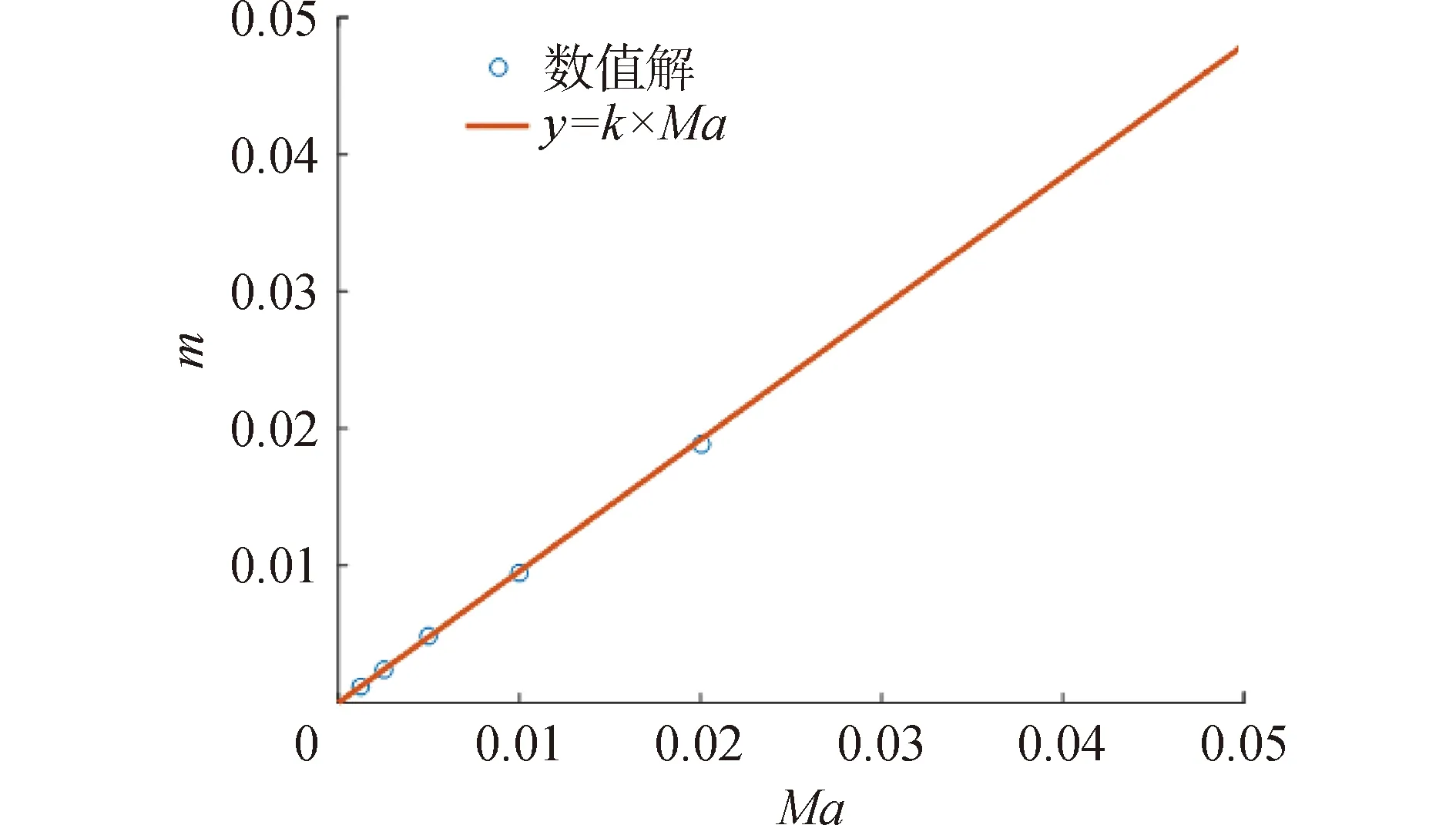
圖12 調制深度隨馬赫數變化規律Fig.12 Variations of modulation depth with Mach number

2.3 尺度波長比影響分析

研究不同尺度波長比L/λ條件下振蕩渦流場對聲場散射和調制作用的影響。對尺度波長比L/λ分別為0.062 5、0.125、0.25、0.5、1時的流聲耦合問題進行計算,不同尺度波長比聲散射指向性隨方位變化關系如圖13所示,對于所計算范圍內,當尺度波長比較小時,指向性圖存在明顯的主瓣和旁瓣,隨著尺度波長比的增大,旁瓣逐漸消失,主瓣逐漸平滑,該規律與剛性球體聲散射類似[15,21]。在尺度波長比較小時,流場速度梯度較大,因而產生較強的散射指向性,而尺度波長比較大時,流場速度梯度較小,散射指向性減弱,不同角度聲壓變化更為平緩。

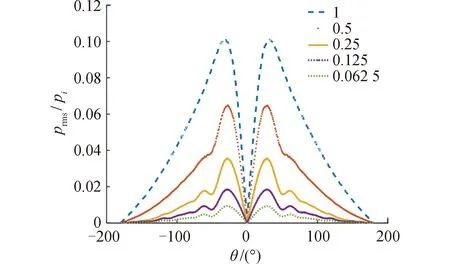
圖13 不同尺度波長比聲散射指向性圖Fig.13 Sound scattering directivity maps of wavelength ratio at different scales

散射截面和調制深度隨尺度波長比變化規律曲線分別如圖14、15所示。在所計算尺度波長比范圍內,散射截面和調制深度會隨著尺度波長比的增加而增加。散射截面與尺度波長比具有接近平方的關系,調制深度與尺度波長比具有接近正比的關系。

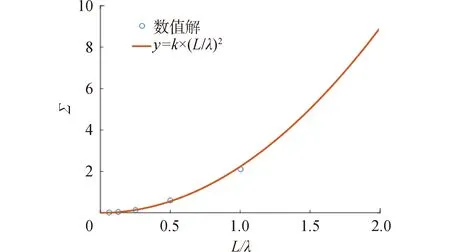
圖14 散射截面隨尺度波長比變化規律Fig.14 Variation of scattering cross section with scale-wavelength ratio

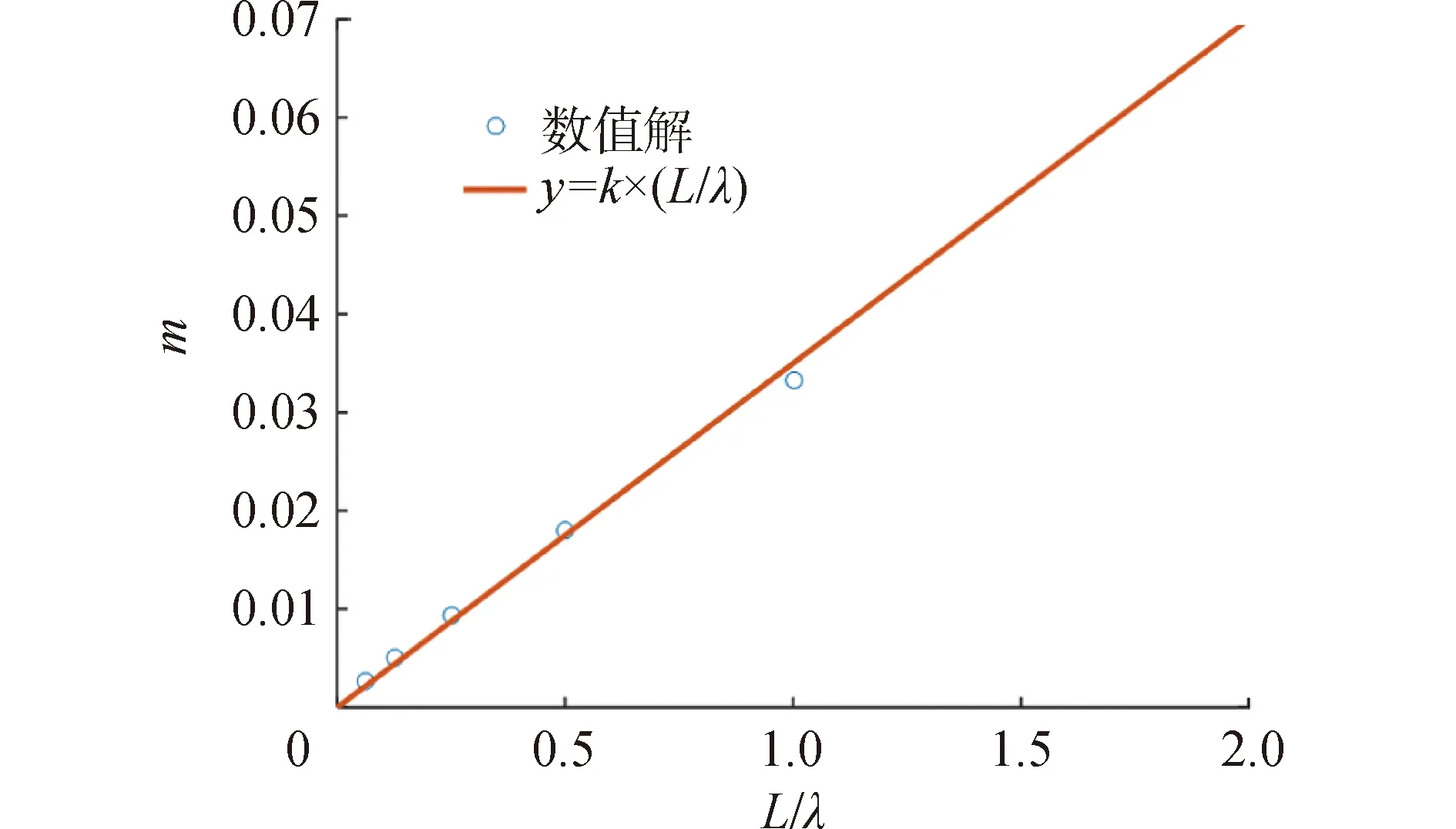
圖15 調制深度隨尺度波長比變化規律Fig.15 Variation of modulation depth with scale-wavelength ratio

2.4 頻率比影響分析

研究不同頻率比f1/f0條件下渦流場對聲場散射和調制作用的影響。對頻率比f1/f0分別為0.008、0.016、0.04、0.08、0.2時的流聲耦合問題進行計算,不同頻率比聲散射指向性隨方位變化關系如圖16所示,對于所計算范圍內,可以看出散射指向性隨著頻率比的改變的規律,同尺度波長比具有一定相似性,即隨著頻率比的降低,旁瓣逐漸減少,主瓣逐漸平滑,不同之處在于頻率比降低到一定程度之后,散射指向性幾乎不再隨頻率比變化而變化。

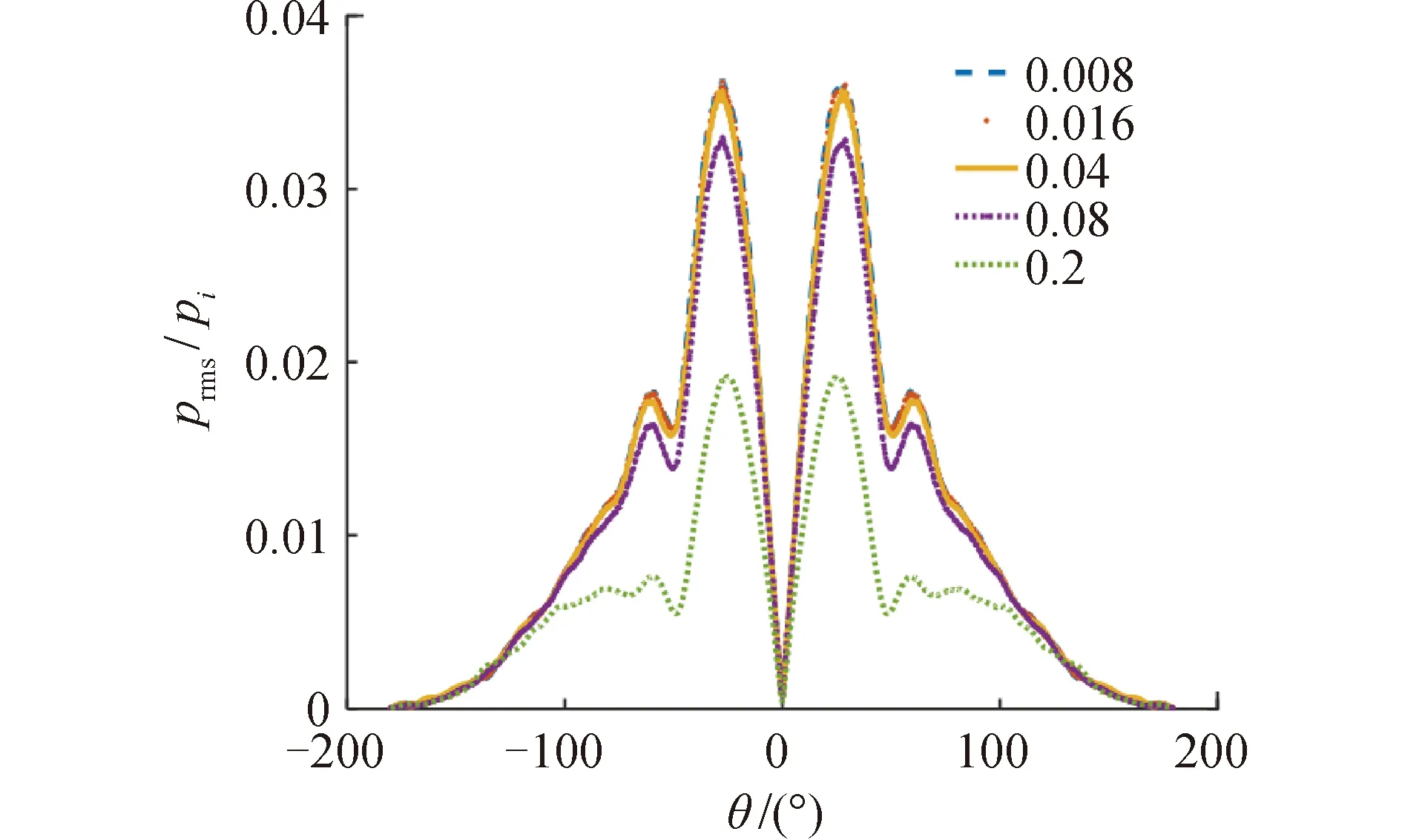
圖16 不同頻率比聲散射指向性Fig.16 Directivity diagram of sound scattering at different frequency ratios

對于所計算范圍內,不同頻率比條件下的流場對聲場的影響存在一極限值,在此將對應的頻率比稱為極限頻率比(f1/f0)lim,高于極限頻率比時,散射截面和調制深度隨頻率比減小而增大,流場對聲場的影響隨頻率比減小而增強,降低到極限頻率比后,散射截面和調制深度幾乎不隨頻率比變化而變化。

為了進一步研究不同頻率比時的聲場變化規律,分析了頻率比f1/f0在0.004～0.2散射截面和調制深度隨頻率比的變化情況,分別如圖17、18所示。散射截面隨頻率比的變化情況呈現3個階段的變化,如圖中Ⅰ、Ⅱ、Ⅲ,極限頻率比(f1/f0)lim約為0.01,在第Ⅰ階段,隨著頻率比降低,散射截面迅速增大。逐漸接近極限頻率比時,進入階段Ⅱ,此時散射截面隨著頻率比降低依然增大,但增大幅度變緩。超過極限頻率比后,在Ⅲ階段,頻率比的改變對散射聲場幾乎沒有影響。

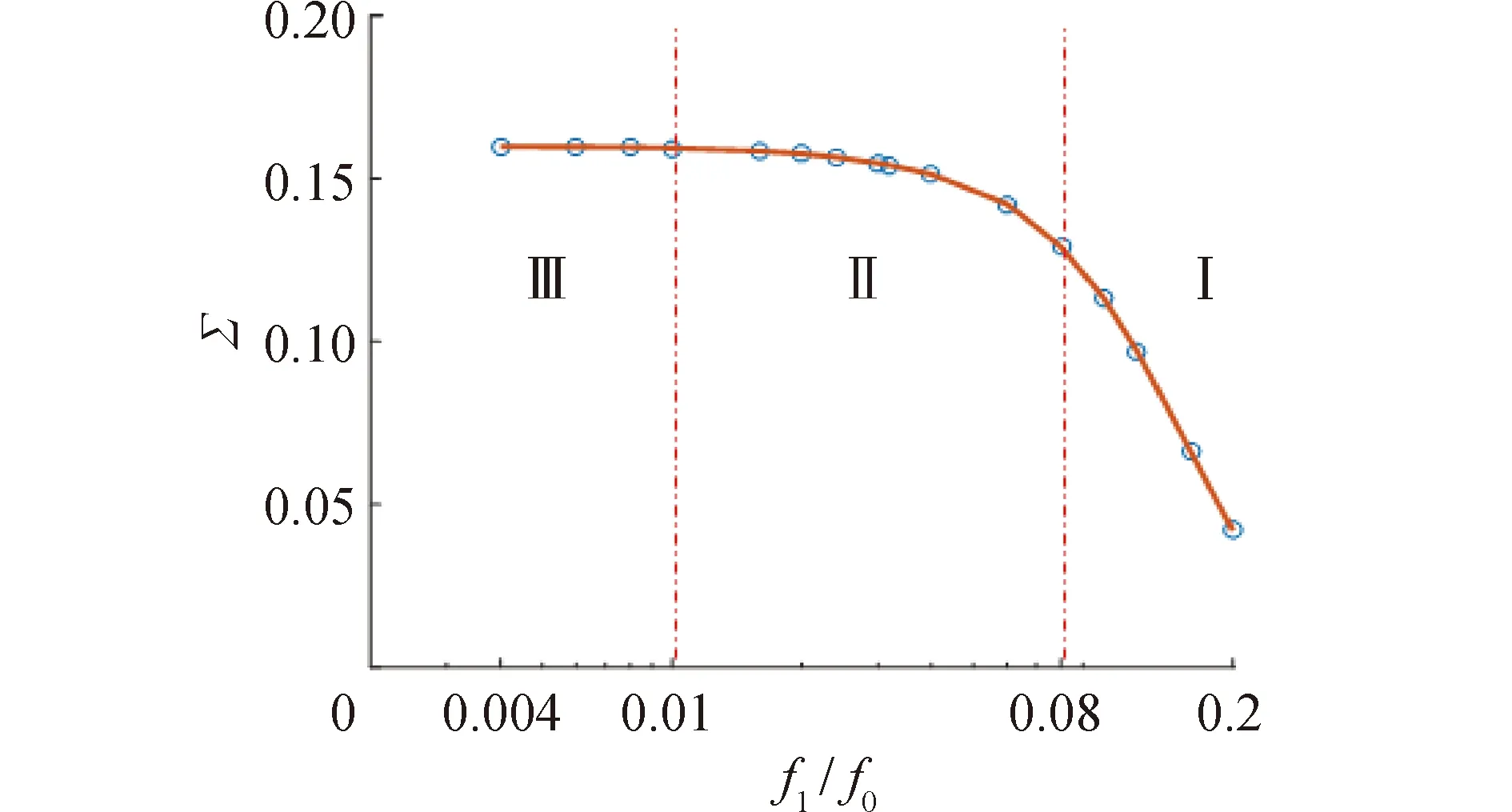
圖17 散射截面隨頻率比變化規律Fig.17 The variation law of scattering cross section with frequency ratio

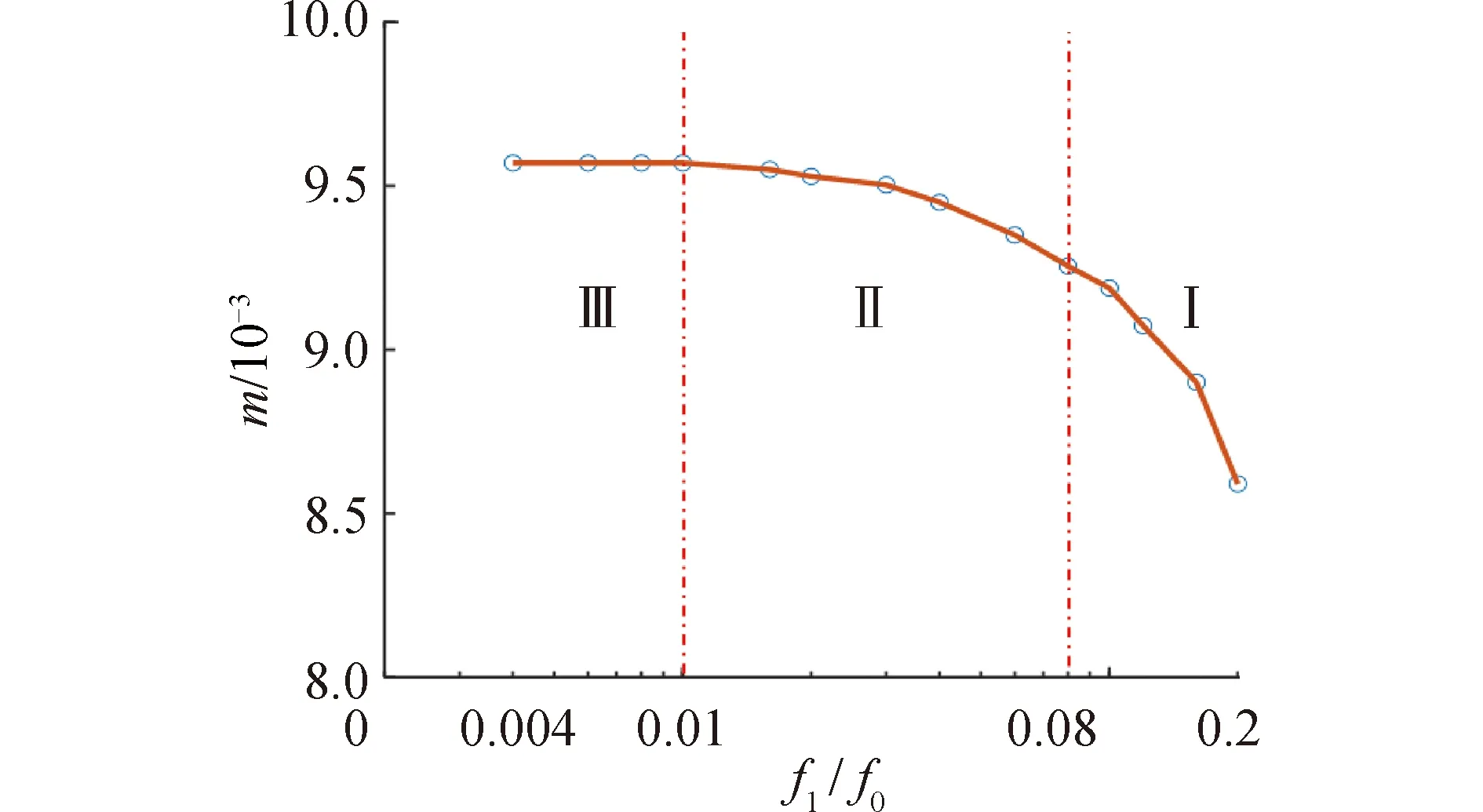
圖18 調制深度隨頻率比變化規律Fig.18 The variation law of modulation depth with frequency ratio

2.5 極限頻率比時聲散射指向性分析

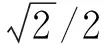
3 結論

1)隨著馬赫數增大,散射指向性曲線形狀基本一致,隨著尺度波長比的增大,散射指向性圖旁瓣逐漸消失,主瓣逐漸平滑。

2)在所計算范圍內,散射截面和調制深度會隨著馬赫數和尺度波長比的增加而增加,散射截面與馬赫數和尺度波長比具有接近平方的關系,調制深度與馬赫數和尺度波長比具有接近正比的關系。

3)不同頻率比條件下的渦流場對聲場的影響存在一極限頻率比,高于極限頻率比時,流場對聲場的散射和調制作用隨頻率比降低而增強,散射指向性圖旁瓣逐漸消失,隨著頻率比的降低,散射和調制作用增強速度變小,降低到極限頻率比后,頻率比的改變對聲場的散射和調制作用幾乎沒有影響。