生活中的不等式

李建華

數(shù)學與我們的生活息息相關，生活中處處有數(shù)學，而大量的不等關系也蘊藏在生活中的每個角落。希望同學們能學著用數(shù)學的眼光去觀察、分析、解決生活中的問題。下面，讓我們從幾個實例中感悟不等式在實際生活中的應用，體驗數(shù)學的應用價值。

例1 小明準備用40元錢購買作業(yè)本和簽字筆。已知每本作業(yè)本6元，每支簽字筆2.2元，小明買了7支簽字筆，他最多還可以買的作業(yè)本數(shù)量為（ ）。

A.5 B.4 C.3 D.2

【解析】設還可以買x本作業(yè)本，利用總價=單價×數(shù)量，結合總價不超過40元，即可得出關于x的一元一次不等式2.2×7+6x≤40，解得x≤[4110]。又因為x為正整數(shù)，所以x的最大值為4。

例2 商店為了促銷某種商品，將定價為3元/件的商品，以下列方式優(yōu)惠銷售：若購買不超過5件，按原價付款；若一次性購買5件以上，超過5件的部分打八折。現(xiàn)有27元錢，最多可以購買該商品多少件？

【解析】設可以購買該商品x件。因為27＞15，所以購買的數(shù)量肯定超過5件。根據(jù)總價=3×5+3×0.8×超過5件的數(shù)量，結合總價不超過27元，即可得出關于x的一元一次不等式3×5+3×0.8（x-5）≤27，解得x≤10，所以最多可以購買該商品10件。

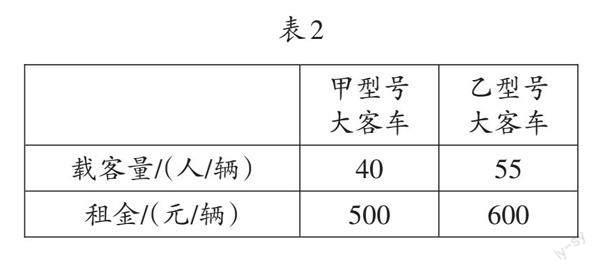
例3 某市居民用電的電價實行階梯收費，收費標準如表1所示：

七月份是用電高峰期，李叔計劃七月份電費支出不超過149元，那么，李叔家七月份最多可用電多少度？

【解析】同學們要先判斷出電費是否超過200度、400度，然后根據(jù)不等關系“七月份電費支出不超過149元”，列不等式。由表1可知，李叔家七月的用電量可超過200度，但不能超過400度，于是可得0.48×200+0.53（x-200）≤149，解得x≤300，即李叔家七月份最多可用電的度數(shù)是300。……