基于車頭時距偏差閾值的公交防串車控制方法

馮壽展 （北方工業大學 電氣與控制工程學院，北京 100144）

0 引 言

目前對于公交防串車問題的研究方法，主要可以分為時刻表控制、站點控制和站間控制三類。劉環宇[1]基于公交車的公共性，用三個約束條件建立了公交車班次優化的可靠模型；黃青霞等[2]提出了一種將駐站策略和限流策略組合的公交防串車控制方法，該策略基于車頭時距閾值，并利用元胞自動機模型分析了控制參數取值對系統性能的影響；陳維亞等[3]考慮到乘客感知時間的因素，提出了基于預測控制的方法；嚴海等[4]以車頭時距平均絕對誤差最小為目標，提出了實時交通速度的控制方法，并在三種公交場景下，通過數值仿真對各類指標進行了評價。

綜合已有研究可知，多種方法組合控制的方式為解決公交串車問題提供了新思路。在公交防串車控制中，車頭時距偏差隨運行距離的增大呈放大趨勢，并且存在車頭時距偏差逐漸增大并伴隨串車現象的拐點。基于此，本文提出了以車頭時距偏差為閾值的公交駐站和限流組合控制方法，以車頭時距偏差和乘客等待時間最小為優化目標，通過粒子群算法計算出最優駐站時間和限流人數，從而有效防止串車現象的發生。

1 公交防串車控制模型

本文以單向公交線路為研究對象，在此路線中共設置Ns個站點，共Nv輛車，共V個班次，發車時間間隔為H，并根據終點處車頭時距偏差小于一半及以上發車間隔得到控制閾值△H，當車頭時距偏差小于閾值時不進行操作，反之則實行駐站或限流控制策略。

1.1 控制閾值

首先將采集到的公交數據采用線性回歸的方法進行處理，圖1記錄了濟寧市16路公交到達終點站時車頭時距偏差超過發車間隔1倍及其以上的車輛班次，以及在各個站點處的車頭時距偏差分布情況。從圖中可以發現，車頭時距偏差與行駛過的站點有關，當起始站附近的站點積累到一定閾值時，會在后續站點中呈逐漸放大的趨勢。

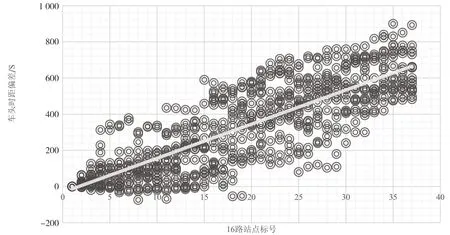
圖1 車頭時距偏差與站點關系

根據圖1設置各站點車頭時距偏差絕對值（|（Di，j-Di-1，j）-（Di，1-Di-1，1）|，Di，j為第i輛公交車離開站點j的時刻）的控制閾值函數為：△Hj=mtj-n，式中△Hj表示站點j的離站車頭時距偏差的控制閾值；j為車站自起點站序號，這里取j∈（2，…，Ns-1），tj為站點j處所花費的時間；m，n均為標定的參數。基于上述分析得出車頭時距偏差控制閾值函數為△Hj=18.86-32.267，R2=0.697 4。

1.2 控制策略

1.2.1 策略選擇

當車頭時距偏差絕對值滿足公式（1）時，不進行任何操作使其自行控制，c為調整參數；當滿足公式（2）時，進行限流操作，限制登車人數；滿足公式（3）時，進行駐站操作，使公交額外駐停一段時間。

1.2.2 目標函數

在公交運營過程中通常將公交車輛運行的穩定性和乘客的等待時間作為優化目標來提高線路運營服務的可靠性。因此本文將公交車i與前車i-1的車頭時距偏差和乘客到達站點的等待時間最小作為目標函數，定義目標函數如下。

式（5）中：ω為車頭時距偏差調整參數，為保障車頭時距偏差和乘客等待時間具有同等的重要性。

乘客等待時間由三部分構成，分別為乘客等待第一輛車的時間、未下車乘客在站點等待公交離站時間和因限流操作使部分乘客等待下一輛車所花費時間。乘客等待時間描述如下。

由于本文設置乘客均勻分布到達，因此乘客平均等待第一輛車的時間為（Di，j-Di-1，j）/2，即：

式（8）中：γj為j站點乘客的到達率。

為公交到站時未下車乘客等待公交駛離站點的時間，若執行駐站策略則會使該等待時間增加，即：

式（9）中：Pdowni，j表示公交i到達站點j時的下車人數；Palli，j為公交i到達站點j時的在車人數；為公交在j站點服務時間。

為執行限流控制使被拒乘客等待下一班車所花費時間，等于被拒人數乘以前后輛車到達當前站點的時間間距，即：

式（10）中：Plimi，j為公交i在站點j處被限制登車的人數。

本文參考黃青霞等[2]提出的方法，后向公交i+1離站時間預測為：

式（11）中：Tnow為當前時刻；Xsj為站點j的位置；xi+1為當前時刻公交i+1所處位置；ta為單位乘客上車花費的時間；vi，j為公交i從j-1站點到站點j行駛的平均速度。

1.2.3 約束條件

a. 公交車停留站點服務時間

公交i在站點j的服務時間由上下車乘客所花費時間的最大值決定，式中：Pupi，j為站點j處最終登上公交車i的人數；tb為單位乘客下車花費的時間；Lj為j點的下車率。

b. 公交離站時間

式（14）中公交i在站點j的離站時間Di，j由兩部分構成，分別為公交i到達站點j的到站時間Ai，j和站點服務時間Tsi，j兩部分。

c. 站點等待人數

公交車i到達站點j時在站點處等待的人數P'upi，j，由離站期間來站人數（Di，j-Di-1，j）*γj和被上一輛車所拒載人數δi-1，j構成。

d. 公交駐站時間

式（16）中：為公交i在站點j的駐站時間；Tmax'為最大的允許駐站時間，最多為4min。

e. 公交限流人數

其中：Plimi.j為公交限流人數；最大限流人數為公交車i到達站點j時的等車人數；最小限流人數受公交承載能力限制，若車內容量能夠滿足所有等車乘客都上車，則為0；C為公交車承載能力。

f. 公交最終上車人數

公交站點最終上車人數不得超過公交車當前的承載容量，即：

若進行限流操作則公交最終上車人數為站點等待人數減去限制登車人數，即：

g. 不允許超車

公交車i在站點j的離站時間要大于公交車i-1在站點j的離站時間。

1.2.4 控制流程

粒子群算法（PSO：Particle Swarm Optimization）是一種通過群體中個體之間的協作和信息共享來尋找最優解的優化算法，本文主要使用該算法快速計算公交駐站時間和限流人數，控制流程如下所示。

Step1 記錄車輛i到達站點j的時間和等車人數，且i＞1，j＞1。

Step2 計算離站時間。

Step3 判斷車頭時距偏差，若符合公式（2）就執行限流操作，使用遺傳算法求解最優限流人數；若符合公式（3）則執行駐站操作，用遺傳算法求解最優駐站時間，否則不進行任何額外操作。

Step4 更新離站時間。

Step5 判斷公交是否到達倒數第二站，即j是否等于Ns-1，如果未到，則j=j+1，返回Step1；如果已到，則轉到Step6。

Step6i=i+1，若i大于V，即為最后班次的公交，則操作結束；若小于V，則返回Step1。

2 仿真實驗及分析

2.1 模擬參數

參考黃青霞等[2]提出的元胞自動機仿真模型，本文以濟寧市16路公交2019年11月11日至11月17日的公交運行數據為研究對象。該路線共有37個停靠站點，運行方向為從北城駕校站到太百湖區公交樞紐站，公交線路總長達22.4km，每隔8min發一趟車，共模擬500min。模型中時間步長為1s；單位元胞長2m，因此1km=500元胞；公交車長10m=5元胞；車速Vmax=5元胞/時間步；調整參數c為0.3。乘客各站點到達率和下車率也應符合實際情況，各站點乘客信息如表1所示。

表1 各站點乘客信息

2.2 閾值調整參數確定

通過對比分析在駐站限流組合控制下不同閾值調整參數c下的評價參數可知，當c=0.1時要綜合優于其他參數，因此本文采用0.1作為實驗的閾值調整參數，如表2所示。

表2 各參數信息

2.3 性能評價

本文對駐站和限流組合控制、駐站控制、限流控制和無控制4種情況進行了仿真實驗，各個控制策略的評價信息如表3所示。

表3 各控制策略評價信息

由表3中可以看出，無論是單一的駐站還是限流控制亦或是駐站限流組合控制，相對于無控制措施而言，在車輛運行穩定性方面都能發揮良好的作用。其中限流控制因需要限制一部分乘客登車以減少公交在站時間，所以行程時間也是三種控制策略中最短的，而被遺留乘客需要等待下一輛車所以導致乘客的等待時間變長。駐站控制則需要在站點處額外停留一段時間，從而使得每輛車的行駛時間都增加了。而駐站限流組合控制考慮到車頭時距偏差和乘客等待時間的影響，根據控制閾值采取兩種控制措施結合的方式在站點及時調整，從而避免后續車頭時距不斷偏離的情況發生，同時減少乘客的等待時間，相較于其他控制策略而言效果最優。

四種控制方法的車頭時距偏差如圖2所示，由圖2（a）可以看出無控制時車頭時距的波動較大，而實施駐站限流組合控制的車頭時距穩定，到站車頭時距偏差基本都保持在70s之內，而圖2（c）和圖2（d）由于采用了單一的控制措施，因此僅能對靠近車輛或者遠離車輛的情況進行改進，不能達到組合控制的效果，但控制后的車頭時距偏差效果已經有了明顯的改善。由表2中車頭時距偏差和其標準差可以看出組合控制相較于無控制在車輛穩定性方面取得了明顯的提高，組合控制下的車頭時距偏差降低了80%，單一駐站控制和限流控制下的車頭時距偏差分別降低了73%和70%。

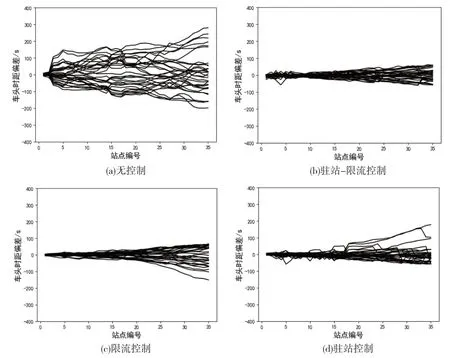
圖2 四種情況下各站點的車頭時距偏差情況

3 結 論

本文提出了一種以車頭時距偏差為閾值駐站與限流相結合的防串車控制方法，以公交到達站點時車頭時距偏差最小和乘客等待時間最短為目標，使用粒子群算法求解最優駐站時間和限流人數，在減少乘客等待時間的同時保證車頭時距偏差穩定，降低了車頭時距偏差在后續站點中持續放大趨勢的產生。仿真試驗中相較于無控制、駐站控制和限流控制策略，駐站限流組合控制在保障車頭時距穩定和降低乘客等待時間方面有了顯著的提升。