面向特征演變環境的標記噪聲魯棒學習算法

張震宇 姜 遠

（南京大學計算機科學與技術系 南京 210023）（zhangzy@lamda.nju.edu.cn）

傳統的機器學習任務通常假設學習環境穩定不變，并且收集的數據標記是高質量的.然而，在實際的應用場景中，數據在開放變化的環境中不斷累積，而且數據標記往往是帶有噪聲的.具體而言，隨著學習環境的變化，數據的特征空間可能發生演變.與此同時，數據的標記可能不準確.這類問題在現實應用中廣泛存在，并且具有重要意義.以環境監測任務為例，研究者在野外部署傳感器以監測種群信息.傳感器不斷收集數據，每個傳感器收集的數值對應著一個特征，所有傳感器收集的數據組合在一起形成了數據的特征空間.由于傳感器使用壽命有限，因此研究人員需要用新的傳感器替換損壞的傳感器.隨著時間的推移，新的特征（新傳感器）出現，舊的特征（到達使用壽命的傳感器）消失，學習要素發生了變化，即數據的特征空間發生了演變.與此同時，由于對數據樣本的人工標注可能存在誤差，數據標記可能存在噪聲.因此使得學習系統具備應對開放環境下特征空間演變和數據標記帶噪的能力變得至關重要[1-2].

隨著數據特征空間的不斷演變，學習模型需要具備處理新特征空間數據的能力，以建立具有泛化能力的學習模型.為此，建立新舊特征空間之間的關系，有效利用舊特征空間的歷史數據是至關重要的.以往的研究通常考慮特征演變環境中的數據流存在特征演變階段[3-4].研究者們通過該階段的數據建立新舊特征空間之間的聯系，從而利用歷史數據幫助學習新特征空間下的分類器.以環境監測為例，如圖1所示，在傳感器到達使用壽命之前，研究者可以提前部署一批新的傳感器用以替代即將失效的傳感器.在此階段，新舊傳感器同時收集數據，因此此時的數據具有新舊特征空間的表示，形成了數據演變階段.為了構建新特征空間上的分類器，研究者們提出了一種基于映射函數的解決思路[3].該方法利用演變階段的數據學習映射函數，在新特征空間上學習分類器的同時，將數據映射回舊特征空間，并復用舊特征空間的模型，輔助構建新特征空間上的分類器.

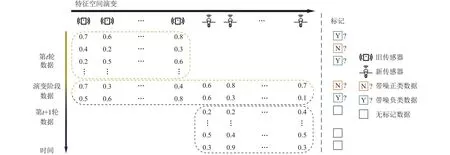
Fig.1 Learning with noisy labeled data in environments with evolving features圖1 特征演變環境下的標記帶噪數據學習

除了數據特征空間的演變外，由于標注過程中可能存在人為誤差，數據的標記往往受到噪聲的干擾[5-6].以野生動物種群監測為例，某些動物可能難以進行準確區分，如獵豹和美洲虎、狼和土狼等[7].當數據特征空間發生演變并且數據標記存在噪聲時，僅僅疊加處理特征演變的算法和處理標記噪聲的算法無法很好地解決這一問題，尤其是很難獲得在理論上具有良好泛化性能保障的分類器.具體而言，為了應對這一難題，一種可行的方案是利用演變階段的數據，首先學習新舊特征空間數據表示之間的映射方式，建立它們之間的聯系.其次，模型可以通過舊特征空間的帶噪標記數據進行魯棒學習，得到分類器.最后，基于學習得到的映射函數，算法將新特征空間的數據映射到舊特征空間上進行預測.然而，由于演變階段的數據較少，通過演變階段數據學習得到的映射函數通常無法完美地還原新特征空間數據在舊特征空間上的表示，因此這種方法的效果會受到映射函數學習質量的制約.在對經過映射函數恢復出的特征表示進行預測時，算法會放大構建映射函數時所引入的誤差，導致分類器性能下降.另外，通過映射函數進行學習的啟發式算法缺乏理論理解，難以獲得具有泛化性能保障的分類器.對于特征空間演變環境下的標記帶噪數據流學習而言，目前還缺乏能夠提供泛化性能保障的算法設計.因此，設計一種有效的算法，能夠同時處理特征空間的演變和數據標記上的噪聲，并在新特征空間上獲得具備泛化性能保障的分類器，成為了當前重要的研究課題.

本文首先形式化了一種特征演變環境下的標記帶噪數據學習問題.具體來說，本文考慮訓練數據以流的形式不斷累積的學習場景，數據特征空間發生演變，同時環境返回的數據標記存在噪聲.在這種情況下，學習者需要不斷對新到達的無標記數據進行預測，并期望在新特征空間上獲得具有泛化能力的分類器.該問題在現實應用中經常遇到，但卻沒有得到深入的研究.針對這類問題，設計具有泛化性能保障的分類器十分重要且具有挑戰性.為了應對這個問題，本文旨在提出一種基于數據差異最小化技術[8-10]的算法來刻畫分類器在新特征空間上的泛化能力.然而，現有的數據差異最小化技術通常只考慮特征空間不變的數據，并且認為數據的標記是準確的，這在本文考慮的學習問題中并不適用.因此，為了學習具有泛化能力的分類器，學習者需要刻畫特征空間演變環境下不同特征空間數據的差異度量，并設計相應的具有理論保障的學習算法.本文在數據標記存在噪聲的情況下，利用演變階段數據，建立了新舊特征空間之間的數據差異度量.基于所提出的容忍標記噪聲的數據差異度量，本文進一步導出了相應的泛化誤差分析結果，并提出了一種基于深度神經網絡的學習算法LREDM（label-noise robust evolving discrepancy minimization）.

本文的主要貢獻包括3個方面：

1） 引入并形式化了特征演變環境下標記帶噪數據的學習問題，盡管這類問題在現實應用中廣泛存在，但卻缺乏深入的研究；

2） 定義了容忍標記噪聲的數據差異度量，并基于此進行了模型泛化性能的分析，給出了模型泛化誤差界的理論保障；

3） 基于提出的理論設計了相應的基于深度神經網絡實現的學習算法LREDM，并且在現實應用的數據集上驗證了所提算法的有效性.

1 相關工作

本文旨在研究特征演變環境下的弱監督學習.在實際應用場景中，訓練數據通常來自于開放且帶噪的環境，因此，學習系統具備適應學習要素變化和標記帶噪數據的能力是至關重要的[1-2]，這也是穩健機器學習[11]和學件[12]的關鍵要求.本文主要關注2個方面：一是特征演變數據學習，二是標記帶噪數據學習.接下來，本節將從這2個方面概述本文的相關工作.

1.1 特征演變數據學習

早期的工作主要研究增量屬性學習[12]和梯形數據學習[13].這些研究考慮數據樣本及其特征維度不斷增加的情況，學習者需要不斷更新模型以應對新增的數據特征.文獻[14]提出了OLSF（online learning with streaming features）算法，以解決數量與特征維度隨時間增加的梯形數據問題.當新特征維度到達時，OLSF算法對不同特征空間執行不同的在線更新規則，使分類器不斷適應新特征維度.與這些研究不同的是，本文的研究問題考慮在新特征出現的同時舊特征可能消失，這為特征空間演變環境下的機器學習帶來了新的挑戰.為了處理特征空間演變的數據流，一系列前沿的研究工作考慮建立新舊特征空間的聯系，進而復用歷史信息輔助對新特征空間數據進行預測和學習.文獻[3]的開創性工作考慮了數據演變階段，其中新舊特征空間的數據同時存在.文獻[3]提出了FESL（feature evolvable streaming learning）算法，通過演變階段學習映射函數，恢復新特征空間上的數據在舊特征空間上的表示.FESL算法在新舊特征空間上構建了2個學習模型，通過在線集成的方式進行預測和學習.后續的工作對演變階段映射方法的學習進行了拓展和探索[15].文獻[4]進一步研究了這一問題，建立了新舊特征空間之間的演變差異，提出了EDM（evolving discrepancy minimization）算法，最小化了分類器在新特征空間數據上的泛化誤差.文獻[16]則考慮了特征繼承性增減環境下的學習問題.其中，新特征空間與舊特征空間的數據存在若干重疊特征，即部分特征表示在舊特征空間和新特征空間內同時存在.文獻[16]提出的OPID（onepass incremental and decremental learning）算法，通過將新特征空間數據映射回舊特征空間，使得舊特征空間數據得以復用進行學習.OFID（online classification algorithm with feature inheritably increasing and decreasing）算法在此基礎上對特征繼承性增減環境進行了深入研究[17].此外，一些研究者考慮了數據流中特征任意增減的情況.例如，文獻[18]提出的OCDS（online learning from capricious data streams）算法和文獻[19]提出的OLVF（online learning from varying features）算法，將數據映射到共享的特征空間中進行統一學習.除此以外，特征演變環境下的在線度量學習[20]、演變數據特征缺失學習[21]同樣得到了研究者關注.然而，大多數特征演變數據學習算法假設數據的標記是準確的，因此難以適應弱監督學習場景，尤其是當數據標記存在噪聲時.

1.2 標記帶噪數據學習

標記帶噪數據學習旨在利用標記帶噪數據訓練出潛在無噪聲數據分布上具有良好泛化能力的分類器.自文獻[22-23]的開創性研究，機器學習領域對標記帶噪數據學習進行了深入廣泛地研究.本文著重研究類別相關的標記噪聲，即噪聲標記的形成機制僅與其真實所屬類別有關.

文獻[6]的研究表明，當噪聲率已知時，通過設置適當的凸代理損失函數，可以在標記噪聲類別下進行經驗風險最小化，從而得到與無噪聲數據分布上最優分類器一致的分類器.文獻[24]通過代理損失分解的方法，提出了樣本標記中心平滑的方法，降低了標記噪聲的負面影響.然而，在實際應用中，學習問題往往面對噪聲率未知的場景.此時，估計噪聲率或噪聲轉移矩陣是處理類別相關的均勻標記噪聲的核心挑戰之一.研究者們提出了一系列假設來估計噪聲轉移矩陣，例如錨詞條件[25]、錨點[26-27]和不可約性[28-29].具體而言，文獻[26]的研究考慮了噪聲率未知的情況，通過估計噪聲率上界的形式，給出了設計凸代理損失函數的方案，并在實驗中驗證了其有效性.文獻[27]假設存在一些經過驗證的準確數據，通過準確標記與無標記數據提取信息來估計噪聲率.文獻[28]對標記帶噪數據做出不可約假設，即存在一些錨點.因此，學習者通過錨點從有噪聲的標記數據中區分并恢復無噪聲分布.通過對數據分布做出一定假設，學習者從數據中估計噪聲率或噪聲轉移矩陣，進而恢復潛在無噪聲數據分布，從而獲得具有泛化性能的學習器.然而，大多數標記帶噪數據學習方法集中在靜態穩定環境中，一旦學習要素發生變化，例如特征空間的改變，導致這些方法往往無法直接適用.

2 預備知識

本節首先介紹特征演變環境下標記帶噪數據學習的場景以及本文用到的符號和相關定義，然后對數據分布差異度量的基本概念及其應用進行回顧.

2.1 問題設定和相關符號

本節考慮特征空間演變環境中的標記帶噪數據學習任務.首先介紹該場景下的數據特點，接著給出相關符號和定義，最后給出問題的形式化.

與文獻[3]的先驅性工作相似，本文假設數據在特征空間演變的過程中存在數據演變階段.如圖1所示，學習者在舊傳感器即將到達使用壽命之前可以提前部署一批新的傳感器，防止發生舊傳感器失靈后無法收集數據的問題.因此，在提前布置好新的傳感器之后，學習者可以收到少量具有新舊2個特征空間表示的數據連接先后2批相鄰但不同特征空間的數據塊.與此同時，由于數據在收集過程中往往存在著噪聲，數據的標記可能是錯誤的.

本文將上述場景形式化為在特征空間演變場景中的標記帶噪數據的學習問題.令Xt?Rdt表示第t輪數據的特征空間，學習者每輪首先收到樣本集合，其中∈Xt.本文考慮特征空間發生演變，因此有dt≠dt+1,t=1,2,…,T.依照傳統在線學習的設置，算法首先需要對樣本進行預測，隨后環境返回樣本的帶噪標記.考慮本文的問題場景，研究二分類學習問題，即樣本的類別空間Y={-1,+1}，但是觀測到的樣本標記存在標記噪聲.對每個樣本xi，本文將樣本未被觀測到的真實標記為yi，被觀測到的噪聲標記為.對于每個真實標記為yi的樣本，它以一定概率以噪聲標記被 觀測到，這一概率根據噪聲率ρ±1定義[6]，具體而言

值得注意的是，噪聲率ρ±1對于算法而言是未知的.

在對t+1輪的數據進行預測時，算法具有第t輪的標記帶噪數據和第t+1輪的待預測無標記數據.因此，根據本文研究場景中的數據特點，每一時刻學習者擁有的數據可以被劃分成3個部分：噪聲標記數據、演變階段數據、待預測數據：

1）來自第t輪特征空間的噪聲標記數據集合，記作

2） 演變階段數據具有新舊2個特征空間Xt和Xt+1上的表示.令表示基于舊特征空間表示的演變階段數據，表示基于新特征空間表示的演變階段數據，其中，.

3） 來自第t+1輪的新特征空間的待預測數據，記作

值得注意的是，演變階段并不會延續太久，因此有k?nt和k?nt+1.以環境監測任務為例，提前部署新傳感器以替換舊傳感器的過程形成了數據演變階段，這一階段的數據數量通常少于舊特征空間的數據.由于演變階段樣本較少，如果直接利用演變階段數據的新特征空間上的表示進行學習，分類器會產生嚴重的過擬合現象.為了緩解t+1輪新特征空間上樣本數量較少的問題，本文考慮利用第t輪舊特征空間的標記帶噪樣本輔助進行學習.表1總結了本文中使用到的主要符號及其定義.

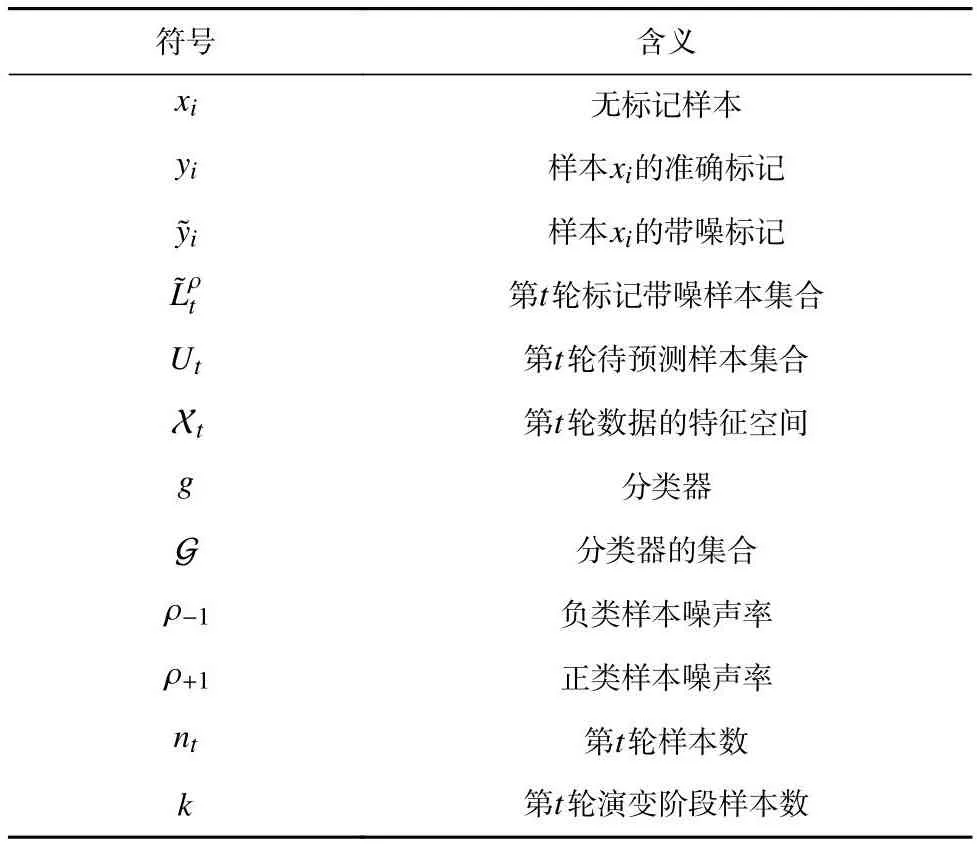
Table 1 Notations and Their Meaning表1 符號和對應含義

對于特征空間演變的標記帶噪數據的學習問題，本文的目標是構建一個在新特征空間上具有泛化能力的分類器.令分類器屬于給定函數族G，其中每個函數gt:Xt-→R.考慮損失函數?:R×Y-→R+和函數g∈G，本文將RD(g)記作分類器的期望風險，記作分類器的經驗風險，

因此，本文的學習目標是對于每一輪收集得到的樣本，構建在新特征空間上具有泛化性能的分類器，即在新特征空間上獲得一個期望風險較小的分類器.

2.2 數據分布差異度量

為了應對特征空間的演變，本文將借助差異最小化技術設計算法.本節回顧這一領域的相關研究內容.對于2個來自不同分布的數據集，研究者們提出了多種差異度量方式，用以刻畫它們之間的差異.基于所提的差異度量，研究者們設計對應算法，將數據差異最小化，進而可以在源數據（source data）上學習分類器，并部署到另一個目標分布（target distribution）對應的數據上.例如，利用KL散度刻畫分布差異的學習方法KLIEP（Kullback-Leibler importance estimation procedure）算法[30]，利用最大均值差異度量分布差異的學習方法KMM（kernel mean matching）算法[31]等.文獻[8]基于所提的HΔH散度給出了一種廣義的差異最小化算法的分析.后續由文獻[9]拓展到了任意損失函數上.文獻[32]進一步定義了Y散度，并基于此給出了更緊的泛化誤差界.這些基于差異的泛化誤差界啟發了差異最小化算法[10].

對于訓練數據集和測試數據集分布不同的問題，學習者希望利用有標記的訓練數據集訓練在無標記的測試數據集上具有良好泛化能力的模型.假設訓練數據與測試數據屬于同一個特征空間，對于一個固定的分類器g∈G 而言，它在2個不同分布P和Q上進行遷移部署的質量可以通過分類器期望損失的差異來度量.一個直觀的差異度量方式就是可以通過對未知的分類器和目標函數的差異取最大值，定義為：

其中RP(·;g′)表示分類器在數據分布P上目標函數為g′的期望損失.

更進一步地，研究者們常會用Y散度[32]來衡量數據分布之間的差異最大值，其定義為：

這一定義依賴于已知的目標函數fP和fQ，它們是分布差異disc(P,Q)的一種推廣.

值得注意的是，這些方法通常假設數據分布在同一個特征空間內，因此不適用于本文考慮的特征空間發生演變的學習場景.

3 理論與方法

本節為特征空間演變環境下的標記帶噪數據學習問題建立理論與方法.為了獲得具有泛化性能保障的分類器，首先重寫了分類器在新特征空間上的泛化誤差，而其中的關鍵要素是在標記存在噪聲的情況下刻畫2個不同特征空間數據之間的差異.基于對分類器泛化能力的分析，本節進行了對應的算法設計，并通過深度神經網絡進行了具體實現.

3.1 容忍標記噪聲的演變差異

對于特征空間演變環境中的學習問題，由于演變階段數據量較少，僅依賴演變階段的標記數據來訓練模型會容易出現嚴重的過擬合現象.因此，在這種情況下，利用舊特征空間上的標記數據變得至關重要.然而，由于新舊特征空間的維度不同，固定特征空間上的數據分布差異度量不再適用.此外，由于數據標記存在噪聲，算法無法直接利用，因此學習者亟需建立容忍標記噪聲的異質特征空間數據差異度量.

為了應對標記噪聲，本文采用樣本加權的方法恢復分類器在潛在無噪聲數據上的真實損失.具體而言，針對每一輪的標記帶噪數據集合，本文定義其加權經驗損失為

其中樣本權重αi定義為

基于式（1）的權重定義，考慮分類器在標記帶噪數據上的加權損失，有引理1成立[6,26].

引理1.對于假設空間中的任一函數g∈G，給定權重α，分類器在標記帶噪數據上的加權期望損失等于該分類器在潛在無噪聲數據上的真實損失，即

證明：根據對期望風險的概率拆分，有：

其中式（6）是根據定義展開的，式（7）是改變數據分布后的概率重加權，式（8）的成立是因為標記噪聲不改變樣本特征的邊際分布，式（9）的成立是根據噪聲率的定義.對于式（9），考慮噪聲正類標記的后驗概率，有：

同理，考慮噪聲負類標記的后驗概率，有：

結合噪聲正類標記的后驗概率結果，可得式（5）成立.

證畢.

引理1證明了標記帶噪數據上的加權經驗風險在期望意義上等于分類器在潛在無噪聲數據上的真實風險.因此，研究者可以通過對權重進行有效估計，設計對標記噪聲具備容忍性的學習算法.

在通過樣本加權處理標記噪聲后，本文進一步考慮復用舊特征空間的標記數據，以輔助構建在新特征空間上具有泛化能力的分類器.在進行針對特征空間演變環境的學習理論分析之前，本文對學習算法的損失函數進行一定的假設.本文考慮損失函數?是非負凸函數，并且滿足以下類似利普希茨的平滑條件.

定義1.損失函數的σ-admissible性質.如果存在σ∈R+使得對于任意2個分類器g,g′∈G和對于所有樣本(x,y)∈X×Y 有式（10）成立，則稱損失函數?對假設空間G 是σ-admissible的.

值得注意的是，式（10）中定義的具有σ-admissible性質的損失函數是較為常見的，包括平方損失、二次損失和許多其他損失函數.具體而言，滿足σ-admissible性質的損失函數具有條件：對于M∈R+： ?g∈G和?x∈X，有|g(x)|≤M成立，且?y∈Y，有|y|≤M成立.式（11）證明有界的最小二乘損失函數是滿足條件的，其他損失函數可以通過類似的證明技術來證明.對于(x,y)∈X×Y 和g,g′∈G，有不等式（11）成立：

其中式（11）的成立是因為損失函數的M有界性質.至此，本文證明了有界最小二乘損失函數是σ-admissible的，其中.

本文基于損失函數的σ-admissible性質，通過構建數據差異的方式，利用舊特征空間上的標記數據輔助構建新特征空間上的分類器.與面向特征演變環境的機器學習的相關前沿研究相似，本文假設數據流中存在數據演變階段，這一階段的數據具有新舊2個特征空間的表示.基于舊特征空間上的標記帶噪數據、新特征空間上的待預測數據，以及演變階段數據，本文提出了容忍標記噪聲的演變差異，衡量了特征演變環境中2個異質特征空間數據分布之間的差異.

定義2.容忍標記噪聲的演變差異.令權重α如式（4）定義所示，對于特征演變環境中的標記帶噪數據流，存在演變階段數據的2個連續數據塊與Ut+1，它們之間的演變差異定義為

其中g′∈Gt，g∈Gt+1是對應的2個分類器，對應著舊特征空間上標記帶噪數據塊的數據分布.

容忍標記噪聲的演變差異衡量了標記帶噪環境中新舊2個不同特征空間的差異，其中關鍵要素在于標記存在噪聲，且數據的特征空間是不同的.定義2中，式（12）中等號右側第1項通過演變階段的對齊數據對齊了分類器g′∈Gt和g∈Gt+1，右側第2項則通過分類器衡量了演變階段數據與新特征空間上數據的差異.直觀地說，容忍標記噪聲的演變差異通過演變階段數據建立了標記帶噪環境中2個不同特征空間數據塊的聯系.

可以看到，本文提出的容忍標記噪聲的演變差異將文獻[32]所提的Y散度差異度量的概念推廣到了特征空間演變、標記存在噪聲的場景，并在特征不發生演變、標記無噪聲時恢復成Y差異度量.值得注意的是，本文所提差異度量沒有使用演變階段數據的標記，因此具有對演變階段標記噪聲的容忍度.

基于所提容忍標記噪聲的演變差異，本文復用了舊特征空間的標記帶噪數據，分析了分類器在新特征空間上的泛化誤差上界.可以證明，通過本文定義的容忍標記噪聲的演變差異，學習者可以直接約束分類器在新特征空間上的泛化誤差.

定理1.泛化誤差界.假設損失函數?是L利普希茨連續和σ-admissible的.對于任何δ＞0，至少以1-δ的概率，有：

證明：對分類器在新特征空間上的期望風險進行考察，有不等式成立：

其中，式（14）是基于Rademacher復雜度分析的泛化誤差上界，式（15）對新特征空間上的目標函數取了最大值.式（16）同樣是基于Rademacher復雜度分析的泛化誤差上界.式（16）由3項內容構成：RDt′(g′)表示分類器在t輪的演變階段數據上的真實期望損失；通過演變階段數據建立了第t輪舊特征空間上標記帶噪數據與第t+1輪新特征空間上待預測無標記數據之間的聯系；衡量了分類器在第t+1輪特征空間數據上，演變階段數據與新特征空間所有數據之間的差異.

這3項可以依次被約束.對于第1項，根據引理1，分類器在標記帶噪數據上的加權期望損失等于分類器在潛在無噪聲數據上的真實期望損失，因此可以將演變階段數據的真實損失通過第t輪的標記帶噪數據的加權經驗損失和復雜度項進行上界.因此，有式（17）成立:

對于式（16）不等號右側中的第2項，算法利用損失函數的σ-admissible性質，對齊不同特征空間上的分類器g′和g.根據損失函數的σ-admissible性質，有式（18）成立：

結合式（16）～（18），可以得證：

定理1證明了第t+1輪新特征空間上分類器的泛化誤差可以被舊特征空間上標記帶噪數據的加權經驗風險及本文所提容忍標記噪聲的演變差異所約束.本文所提的容忍標記噪聲的演變差異通過樣本加權的方式對抗了標記噪聲，通過在演變階段進行分類器對齊的方式橋接了不同的特征空間.如果樣本標記是準確的，則可將α設置為1.通過對標記帶噪數據進行重新加權，本文提出的算法可以獲得對潛在真實損失的無偏估計（見引理1）.相比之下，啟發式的對抗標記噪聲的方法，如梯度裁剪[33]和丟棄大損失值樣本[34]等，難以具備這樣的能力，因此無法約束分類器在新特征空間上的期望損失的上界.

在證明定理1時，損失函數的σ-admissible性質至關重要.如定義1及式（11）中的分析所述，這一性質十分常見，適用于二次損失函數或者具有有界假設空間的損失函數.通過利用損失函數的σ-admissible性質，算法可以利用演變階段的數據，將異質特征空間上的分類器g′和g進行對齊.在對齊分類器之后，即使標記帶噪數據來自不同的特征空間，算法也可以復用舊特征空間的歷史數據對當前數據進行學習.

3.2 算法設計

通過本文所提容忍標記噪聲的演變差異，本文分析了分類器在新特征空間上的泛化誤差上界.這一理論分析啟發了本文的算法設計.本節將提出對應的算法，直接優化分類器在新特征空間上的泛化誤差，構建具有良好泛化性能的分類器.算法首先對權重α進行估計，用以處理標記噪聲；然后，算法將最小化標記帶噪數據上的加權經驗風險和容忍標記噪聲的演變差異用以建立具有泛化能力的分類器.

基于本文所提演變差異和定理1中的泛化誤差界，本文利用深度神經網絡的特征提取能力，設計了容忍標記噪聲的演變差異最小化算法LREDM.本文主要關注特征空間演變的2個連續數據塊的學習問題，因此下文僅詳細敘述在特征演變發生時對應的學習方案.

針對標記噪聲，算法估計權重α后進行加權經驗風險最小化.根據式（4）中權重的定義

算法需要估計條件概率和噪聲率ρ±1.本文采用密度比估計（density ratio estimation，DRE）的方法來估計條件概率.密度比估計是一種顯著減少核密度估計維度災難的方法，它可以精確地估計高維變量的密度比.常用的3種密度比估計方法包括矩匹配法、概率分類法和比值匹配法.由于概率分類方法可能引入較大的近似誤差，因此研究者在實際算法應用中更多地采用矩匹配或者比值匹配方法[35].其中，密度通常通過線性或非線性函數進行建模.如果選擇的再生核希爾伯特空間比較適當，那么矩匹配和比值匹配方法的近似誤差可以很小.這些方法在實踐中被廣泛證明了有效性[36-37].

對于條件概率，本文采用比值匹配法中被廣泛應用的KLIEP法[30]來估計.給定樣本和對應的帶噪標記，KLIEP返回其條件概率.在獲得樣本的條件概率后，依照文獻[26]中的結論，噪聲率滿足：

因此，本文通過對應類別在標記帶噪數據上取最小條件概率的方法

來估計噪聲率ρ±1.

在對權重α進行估計后，算法最小化分類器在標記帶噪數據上的加權經驗風險和容忍標記噪聲的演變差異.定理1中的泛化誤差分析對應優化目標

觀察式（19）和式（20）可以發現，優化問題可以看作是一個極小極大優化問題，其中最小化分類器g,g′∈G最小化泛化誤差，而最大化分類器ft+1∈Gt+1搜索演變差異的最壞情況.這類學習問題在基于對抗生成的遷移學習中被廣泛研究，具有成熟的優化算法[38-39].因此，本文通過對抗網絡DANN[38]來優化分類器的加權損失和容忍標記噪聲的演變差異.具體而言，算法交替優化式（21）和式（22），直到損失收斂.

通過最小化舊特征空間上標記帶噪數據的加權經驗風險以及容忍標記噪聲的演變差異，算法可以在新特征空間數據上獲得一個具有良好泛化能力的分類器.由于權重α的優化問題和分類器g′和g的優化問題不是聯合凸的，因此算法首先求解權重α來緩解標記噪聲問題，然后優化極小極大優化問題.

容忍標記噪聲的演變差異最小化算法的流程如算法1所示.

算法1.容忍標記噪聲的演變差異最小化算法.

輸入：每輪數據Lρt和下一輪待預測數據Ut；

輸出：分類器g∈Gt+1.

①遍歷t=1,2,…,T；

② 通過KLIEP算法估計式（4）中權重α；

③ 收到無標記數據Ut+1；

④ 通過DANN算法優化式（21）和式（22）的極小極大優化問題；

⑤ 獲得gt+1并預測Ut+1；

⑥ 收到標記帶噪數據并存儲；

⑦結束.

4 實驗與結果

本節測試了所提算法LREDM在現實應用場景中的性能表現.本節實驗在合成數據集和多個現實應用數據集上將所提算法與前沿的基準算法進行了對比.具體而言，本節實驗旨在回答3個問題：

1）合成數據分析.所提算法是否在數據標記帶噪的情況下，在特征空間演變的環境中有效地建立了2個異質特征空間的差異度量.

2）基準算法對比.所提算法在各類現實場景中的數據集上的表現是否優于其他前沿的基準算法.

3）消融實驗研究.所提算法的每個模塊是否都能夠對算法性能帶來提升.

本節實驗采用基準數據集，并通過對其進行修改，模擬特征演變環境的標記帶噪數據流.為了滿足實驗數據對于動態特征空間的要求，本節實驗將所使用的數據集原始特征空間進行劃分.在每個時刻，實驗使用基準數據集中不同的特征空間，并在相鄰時間段中插入少量全特征空間數據，以模擬演變階段數據，在2個特征空間上都具有特征表示.針對類別相關的標記噪聲，本節實驗考慮二分類問題，對于某一類樣本，以一定概率將其標記翻轉為另一個類別.需要注意的是，2個類別的標記翻轉概率可以不同.為了測試算法的有效性，本節實驗通過隨機采樣的方式和通過基準數據集生成不同特征演變的標記帶噪數據流，并在不同數據流上測試算法的平均表現結果.本節對每個數據集進行隨機采樣，生成10條數據流，并基于這10次結果的平均值和標準差來報告最終的實驗結果.針對每條數據流，本節考慮發生1次特征空間演變，并在新特征空間上測試算法的實驗結果.

本文在包括RFID，Amazon，Reuters數據集以及其中包含的子數據集的公開數據集上進行試驗，這些數據集分布在多個現實應用領域.

1）RFID數據集[3].該數據集由傳感器收集的物體RFID數據（特征）和物體的實際位置（標記）組成.由于物體不斷到達，傳感器收集的RFID數據形成了數據流.在傳感器達到使用壽命之前，學習者會在舊傳感器附近放置新的傳感器，因此數據流的特征空間發生了演變.在本節實驗中，位置索引被分為2類以生成相應的標記.對于舊特征空間數據標記，本節實驗將其標記以10%的概率進行均勻翻轉以模擬標記噪聲.根據數據的時間戳信息，數據流的前40%是舊特征空間數據，接下來的20%是演變階段數據，最后40%是新特征空間數據.

2） Amazon數據集[40].該數據集包含用戶在2006—2008年對亞馬遜上產品的評價和對應用戶的質量評分.本節實驗采用了該數據集中的3個子數據集，分別是Books，Movies和CDs.學習者希望根據用戶的評價（特征）判斷用戶的質量（標記）.用戶不斷使用這個平臺，形成了數據流.隨著時間的推移，舊的產品下架，新的產品上架，因此數據流的特征空間發生了演變.本節實驗將部分活躍用戶對歷史商品和當前商品的評分作為特征空間演變數據流中的數據演變階段.實驗根據用戶評價的質量將用戶分為2類，從而生成了一個二分類任務，并添加了10%的均勻標記噪聲.根據數據的時間戳信息，數據流的前40%為舊特征空間數據，接下來的20%是演變階段數據，最后40%是新特征空間數據.

3） Reuters多語言數據集[41].該數據集包含5種語言的約一萬篇文檔.由于每種語言特征表示不同，因此同一文檔的不同翻譯版本對應著不同的特征空間，本節實驗以此模擬特征空間演變的數據流.本節實驗將舊特征空間數據的20%設置為演變階段數據，并在新特征空間找到其對應表示.對舊特征空間數據標記，本節實驗將文本標簽分為2類，并將標記以10%的概率均勻翻轉，用以模擬標記噪聲.所有文檔都使用TF-IDF特征表示，本節實驗基于文檔的TF-IDF特征進行主成分分析（PCA），提取了文檔的主要特征.實驗部分所用數據集的相關統計信息如表2所示.

Table 2 Statistics of the Datasets表2 數據集的統計信息

對于LREDM算法的實現，本節實驗將采用2個神經網絡分別作為最小化分類器和最大化分類器，每個網絡都包含5層全連接層，并以ReLU函數作為激活函數.本節實驗將使用衰減學習率的在線隨機梯度下降（SGD）對模型進行訓練，學習率設置為0.004，正則化權重衰減為0.005.

4.1 合成數據分析

本節首先在合成數據上對所提算法進行分析，測試容忍標記噪聲的演變差異在度量異質特征空間的標記帶噪數據塊上的度量性能.

在本節實驗中，采用高斯分布生成數據，可以通過調整均值和方差來控制數據的差異度.因此，可以通過對比算法對不同差異度的數據集的處理效果，來評估算法的差異度量能力.直觀上來看，算法的差異度量能力越強，就越能夠準確反映數據之間的真實差異.因此，本節實驗將通過對合成數據進行分析，測試所提算法在度量異質特征空間的標記帶噪數據塊上的度量性能.

本節實驗通過對高斯分布進行采樣生成數據，合成了3組數據集.每組數據集都包括2個不同特征空間的數據集合：一個是三維的數據集合，另一個是二維的數據集合.為了模擬特征空間的演變，本節實驗將二維數據作為舊特征空間數據，將三維數據作為新特征空間數據.同時，二維數據和三維數據分別從不同均值的標準高斯分布中進行采樣，以模擬不同差異度的學習任務.

1）任務1：二維數據中（舊特征空間），正類數據從Nx([1,1])中生成，負類數據從Nx([-1,-1])中生成；三維數據中（新特征空間），正類數據從Nx([1,1,1])中生成，負類數據從Nx([-1,-1,-1])中生成；

2）任務2：二維數據中（舊特征空間），正類數據從Nx([1,1])中生成，負類數據從Nx([-1,-1])中生成；三維數據中（新特征空間），正類數據從Nx([1,-1,1])中生成，負類數據從Nx([-1,1,-1])中生成；

3） 任務3：二維數據中（舊特征空間），正類數據從Nx([1,1])中生成，負類數據從Nx([-1,-1])中生成；三維數據（新特征空間），正類從Nx([-1,-1,-1])中生成，負類數據從Nx([1,1,1])中生成；

通過計算，可以發現在三維特征空間中，從任務1到任務3，同類數據的類中心距離不斷增大，因此可以認為數據的差異度在一定程度上是不斷增大的.對于每個任務，本節實驗生成了1 000個舊特征空間上的三維樣本和800個新特征空間上的二維樣本，并隨機選擇了200個樣本作為演變階段的數據.

下文將對比不同算法的數據差異度量能力.當數據特征空間發生演變時，一個自然的做法是通過演變階段數據建立2個特征空間之間的映射，以復用舊特征空間上的數據和學習模型[3].直觀上來說，如果新舊特征空間上的數據十分相似，那么映射誤差應該很小，即算法可以通過映射矩陣將新舊特征空間上的數據接近無損地轉換.為了與本文所提演變差異進行對比，下文將基于映射方法建立的新舊特征空間數據之間的重構誤差稱為映射誤差.記學習后的映射函數為M，映射誤差可表示為：

映射誤差衡量了映射函數的數據恢復能力.假設存在一個完美的映射函數，它可以將新舊特征空間之間的表示一一映射，那么通過這個映射函數，算法可以完美恢復出新特征空間數據在舊特征空間上的表示，即映射誤差為零.與演變差異的度量方式類似，當數據越相似時，映射誤差越小.對于本文提出的基于演變差異最小化的算法，本文直接采用演變差異作為衡量指標，度量所提算法所構建的新舊特征空間之間的數據差異.

本節針對3個合成任務測試了LREDM算法和FESL算法的性能.由于數據存在噪聲，本文統一采用IW算法對標記帶噪數據進行加權處理后提交對比算法.由于這2個衡量方式的量綱不同，無法直接比較，因此本節將所有結果進行歸一化后，通過圖2展示它們在這3個任務上的差異.

Fig.2 Date relative discrepancy exhibited by FESL and LREDM圖2 FESL和LREDM展示的數據相對差異

總體而言，本文提出的LREDM算法表現更加準確.具體來說，任務1是3個學習任務中最簡單的，因為新特征空間數據只是舊特征空間數據的邊際分布.圖2表明任務1的演變差異明顯小于任務2和任務3，這符合直覺.相比之下，FESL算法在任務1中報告了最大的映射誤差.對合成數據的分析表明，LREDM的演變差異能夠在數據標記存在噪聲的情況下恢復異質特征空間數據塊之間的差異，并為特征空間演變環境下的標記帶噪數據學習問題提供了更準確的差異度量方法.

4.2 基準算法對比

本節對所提的LREDM算法在現實應用中的表現進行了測試，主要考慮標記帶噪數據和特征空間演變的情況.與此同時，本節還將LREDM算法與前沿算法的性能進行了比較.

本節實驗在3個數據集上模擬了8個標記帶噪數據學習任務，并與6種前沿基準算法進行了比較.這些任務都涉及特征空間的演變.其中，FESL，EDM和OLVF算法是在特征空間演變環境下的前沿學習算法，能夠有效處理特征空間變化下的學習任務.然而，這些算法并未考慮標記噪聲對學習的負面影響.因此，本節實驗添加了額外的標記噪聲校正機制，以進行公平比較.具體而言，本文采用重要性加權（Importance weighting, IW）機制和使用高置信度（high confidence, HC）樣本機制對基于映射的代表性算法FESL算法進行了調整，并將這2種算法分別命名為FESL+IW和FESL+HC.對于FESL+IW算法，本節實驗首先對舊特征空間的標記帶噪樣本進行重加權，然后使用FESL算法進行學習；對于FESL+HC算法，本節實驗首先在舊特征空間上訓練一個分類器，清除置信度低于閾值的標記樣本，然后使用FESL算法進行學習.除了這2種算法外，本節實驗還引入了另一個基準算法IWTS進行兩階段學習.與LREDM算法相同，IWTS算法采用了分塊學習預測的方法，并直接結合了特征演變數據學習和標記帶噪數據學習的方法作為本文研究問題的基準算法.IWTS算法首先使用IW在舊特征空間數據上訓練模型，然后為演變階段數據賦予偽標記，基于演變階段的偽標記數據訓練第2階段模型，并對新特征空間樣本進行預測.

表3中展示了LREDM算法與對比算法在各個實際應用數據集上的平均準確率比較.實驗結果表明，LREDM算法在8個學習任務中均取得了最高的平均準確率，這表明LREDM算法是在特征空間演變環境中針對標記帶噪數據學習任務的一種可行方案.相比于基于映射的算法，LREDM算法具有更好的性能，因為它更準確刻畫了異質特征空間中標記帶噪數據塊之間的差異，并且直接最小化期望風險的上界.此外，實驗結果還表明，LREDM算法總是優于TSIW算法.這是因為在現實世界場景中，演變階段的數據通常較少，很難學到準確的映射函數.

Table 3 Average Accuracy and Standard Deviation of Seven Algorithms on Different Datasets表3 7種算法在不同數據集上的平均準確率與標準差%

本節實驗還在語言數據集上進行了實驗，測試了LREDM算法在文本分類場景中的性能.表3中EN-FR，FR-SP，GR-IT，IT-GR這4個數據集展示了LREDM算法與前沿對比算法在文本數據模擬的學習任務上的實驗結果.實驗結果顯示，在4個文本分類任務中，LREDM算法取得了最高的平均準確性，驗證了該算法在文本類現實應用中的有效性.

本節實驗同樣測試了LREDM算法在不同噪聲率下的有效性.該實驗在Movies數據集和EN-FR數據集上進行，并采用不同的噪聲率來評估LREDM算法的性能.表4展示了LREDM算法和IWTS算法在4種不同噪聲率下的平均準確率和標準差.例如，“0.3/0.1”表示將正類數據以30%的概率錯誤地標記為負類，同時將負類數據以10%的概率錯誤地標記為正類.IWTS算法作為對比算法在基準對比實驗中表現出色，因此也在表4中列出.如表4所示，LREDM算法在不同噪聲率下均取得了更好的實驗效果，驗證了LREDM算法在不同噪聲率環境下的魯棒性.

Table 4 Average Accuracy and Standard Deviation of Two Algorithm on Datasets with Varying Noise Rates表4 2種算法在2種數據集上不同噪聲率下的平均準確率與標準差%

4.3 消融實驗

本節實驗在Reuters多語言數據集上對LREDM算法的每個組成部分進行了有效性測試.LREDM算法中的關鍵模塊包括對標記帶噪數據權重的估計（即噪聲率估計）、對標記帶噪數據上的加權經驗風險和容忍標記噪聲的演變差異的最小化.其中，與權重估計相關的模塊是IW算法，沒有加入IW算法的對比方案將標記帶噪數據的標記視為準確的，并直接進行優化.在消融實驗中，本文所提算法被記作LREDM（加權）；而不加入IW模塊（不對標記噪聲進行特殊處理）的對比方案被記作LREDM（不加權）.

本節實驗測試了LREDM算法在Reuters多語言數據集上6對不同語言之間進行特征空間演變的標記帶噪數據學習.圖3展示了LREDM算法在這些任務中的加權經驗風險、容忍標記噪聲的演變差異和平均準確率隨迭代次數的變化情況.實驗結果表明，隨著演變差異的減少，LREDM算法在這6項任務中的平均準確率均有所提高，這驗證了最小化容忍標記噪聲的演變差異對于特征空間演變環境中標記帶噪數據學習問題的重要性.LREDM（加權）算法通過學習權重對標記帶噪數據進行去噪，然后通過最小化容忍標記噪聲的演變差異來減小異質特征空間的數據差異.實驗結果顯示，與不帶標記噪聲進行處理的對比方案LREDM（不加權）相比，通過應用IW算法學習權重的LREDM（加權）算法獲得了具備更好泛化性能的分類器.對于存在標記噪聲的學習問題，IW算法可以緩解標記噪聲帶來的影響.因此，消融實驗的結果驗證了本文所提的容忍標記噪聲的演變差異度量的有效性，并驗證了LREDM算法中每個組件的有效性.

Fig.3 Weighted empirical risk, label noise robust evolving discrepancy and average accuracy of LREDM algorithm on six groups of experiment simulated by Reuters dataset圖3 LREDM算法在Reuters數據集模擬的6組實驗上的標記帶噪數據的加權經驗風險、容忍標記噪聲的演變差異和平均準確率

因此，通過對LREDM算法在Reuters新聞分類任務上的消融實驗，本節驗證了LREDM算法中每個組件的有效性.

5 結 論

本文研究了在特征空間演變環境下的標記帶噪數據學習問題，這個問題在實際應用中非常重要且普遍存在.由于數據標記存在噪聲并且特征空間可能演變，如何設計學習算法，有效利用舊特征空間中的標記帶噪數據，使得分類器在新特征空間上具有良好的泛化能力，是一個極具挑戰性的問題.為了應對這一挑戰，本文提出了容忍標記噪聲的演變差異來建立具有不同特征空間的連續數據塊的差異度量，并且分析了分類器在特征空間演變的標記帶噪數據流上的泛化誤差.基于所提理論，本文設計了一種名為LREDM的演變差異最小化算法，并使用深度神經網絡進行實現.通過對合成數據的分析研究，本文驗證了所提出的容忍標記噪聲的演變差異可以建立異質特征空間的標記帶噪數據塊之間的差異度量.同時，多個實際應用數據的實驗表明了本文所提出的算法在性能和穩健性方面的優越性.

本文未來的工作主要集中在2個方面：首先，當前所提出的算法在每一輪中需要求解一個極小極大化的優化問題，這一求解過程耗時較多.因此，如何進一步降低算法的運行時間，以更好地適應數據流學習是下一步重要的研究方向.其次，本文考慮了與樣本無關的均勻標記噪聲，但現實應用中的標記噪聲往往更為復雜.因此，如何建立更加有效的求解算法以應對現實應用中復雜的標記噪聲，是未來的重要研究課題.

作者貢獻聲明：張震宇負責提出模型，完成實驗、初稿寫作和論文修改；姜遠負責寫作指導和修改審定.