挖掘圖形特征　確定解題路徑

郭海萍　林新建

解析幾何問(wèn)題一直是數(shù)學(xué)高考的難點(diǎn)，它的“難”在于“運(yùn)算”，這給學(xué)生的解答帶來(lái)較大的挑戰(zhàn)．為此，教學(xué)中教師應(yīng)引領(lǐng)學(xué)生學(xué)會(huì)運(yùn)用數(shù)學(xué)抽象的方法，借助直觀(guān)想象，從問(wèn)題中的條件，挖掘其幾何圖形特征，進(jìn)而選擇合理的解題路徑，將問(wèn)題得以簡(jiǎn)便求解．本文以2022年新高考Ⅰ卷一道試題為例，就如何基于數(shù)學(xué)抽象，借助直觀(guān)想象，挖掘圖形特征指引解題進(jìn)行探析，與同仁交流．

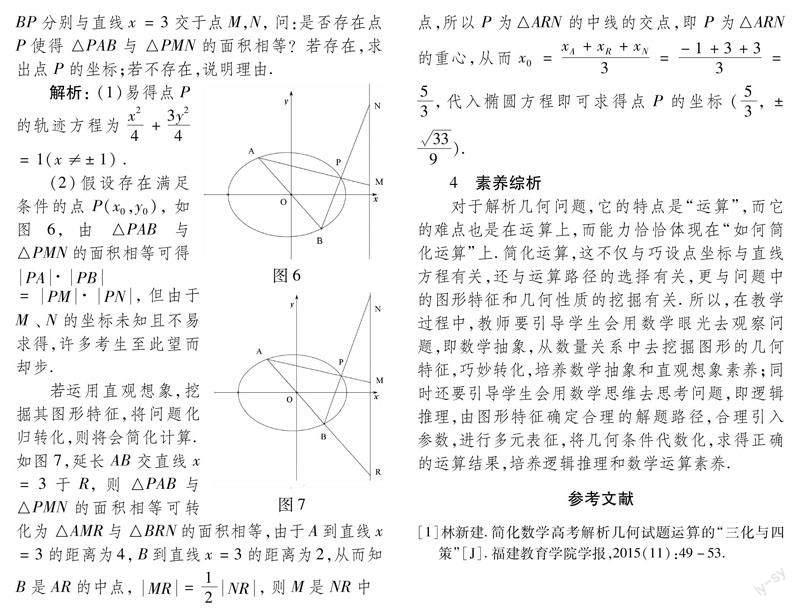
若運(yùn)用直觀(guān)想象，挖掘其圖形特征，將問(wèn)題化歸轉(zhuǎn)化，則將會(huì)簡(jiǎn)化計(jì)算．如圖7，延長(zhǎng)AB交直線(xiàn)x=3于R，則△PAB與△PMN的面積相等可轉(zhuǎn)化為△AMR與△BRN的面積相等，由于A(yíng)到直線(xiàn)x=3的距離為4，B到直線(xiàn)x=3的距離為2，從而知B是AR的中點(diǎn)，MR=1/2NR，則M是NR中點(diǎn)，所以P為△ARN的中線(xiàn)的交點(diǎn)，即P為△ARN的重心，從而x0=xA+xR+xN/3=－1+3+3/3=5/3，代入橢圓方程即可求得點(diǎn)P的坐標(biāo)（5/3，±33/9）．

4 素養(yǎng)綜析

對(duì)于解析幾何問(wèn)題，它的特點(diǎn)是“運(yùn)算”，而它的難點(diǎn)也是在運(yùn)算上，而能力恰恰體現(xiàn)在“如何簡(jiǎn)化運(yùn)算”上．簡(jiǎn)化運(yùn)算，這不僅與巧設(shè)點(diǎn)坐標(biāo)與直線(xiàn)方程有關(guān)，還與運(yùn)算路徑的選擇有關(guān)，更與問(wèn)題中的圖形特征和幾何性質(zhì)的挖掘有關(guān)．所以，在教學(xué)過(guò)程中，教師要引導(dǎo)學(xué)生會(huì)用數(shù)學(xué)眼光去觀(guān)察問(wèn)題，即數(shù)學(xué)抽象，從數(shù)量關(guān)系中去挖掘圖形的幾何特征，巧妙轉(zhuǎn)化，培養(yǎng)數(shù)學(xué)抽象和直觀(guān)想象素養(yǎng)；同時(shí)還要引導(dǎo)學(xué)生會(huì)用數(shù)學(xué)思維去思考問(wèn)題，即邏輯推理，由圖形特征確定合理的解題路徑，合理引入?yún)?shù)，進(jìn)行多元表征，將幾何條件代數(shù)化，求得正確的運(yùn)算結(jié)果，培養(yǎng)邏輯推理和數(shù)學(xué)運(yùn)算素養(yǎng)．

參考文獻(xiàn)

［1］林新建.簡(jiǎn)化數(shù)學(xué)高考解析幾何試題運(yùn)算的“三化與四策”［J］．福建教育學(xué)院學(xué)報(bào)，2015（11）：49-53.

（本文系福建省教育科學(xué)“十四五”規(guī)劃2022年度課題《基于素養(yǎng)導(dǎo)向的高中數(shù)學(xué)幾何主題單元教學(xué)策略研究》（FJJKZX22-175）階段性成果．）