“傳球”問題縱橫談

山東省桓臺第一中學 蘇同安

對于數學問題,不能僅滿足于會做或是用了幾種方法解出;對于課堂教學容量也不能只是用“題量”或內容的多少,甚至是交流的多少來體現.課堂教學更重要的是在注重過程的基礎上產生了多少有價值的“思維量”,是否進行了或“追根求源”或“橫縱拓展”的探究活動.下面通過在教學中對一個數學問題的思考和探究來說明這一點.

1 問題呈現

問題甲、乙、丙三人傳球,由甲開始發球,并作為第一次傳球,經過5次傳球后,球仍回到甲手中,則不同的傳球方式共有多少種?

下面闡述在課堂教學中,如何引領學生從對問題的各種解決方法入手,由特殊到一般、橫向到縱向來進行思考、探究和總結.希望對探究和解決其他數學問題帶來一些啟迪作用,幫助學生更加深刻地認識數學問題的本質,體悟數學思想方法的價值.

2 幾種解法

以下是上述問題的幾種解決方法.

方法一：樹圖列舉法.

甲第一次傳球是給乙的傳球方式(如圖1所示), 共5種情況.

圖1

同理,甲若第一次傳球是給丙,則同樣有5種方式.故所有傳球方式共10種.

方法二：分類圖解法.

甲、乙、丙三人按圖2所示位置站立.

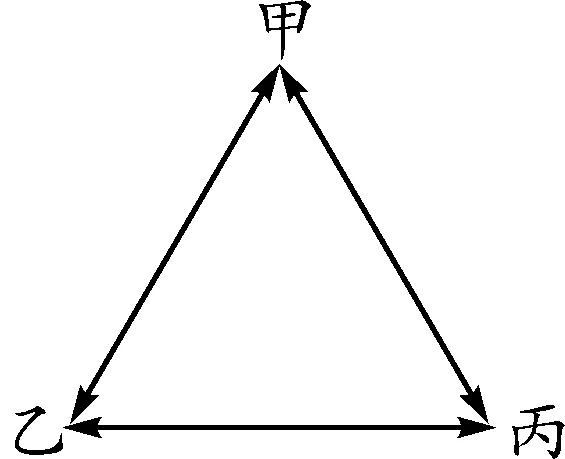
圖2

下面列出甲第一次傳球是給乙的傳球方式,共5種情況,如圖3-1,3-2,3-3,3-4,3-5所示.

圖3-1

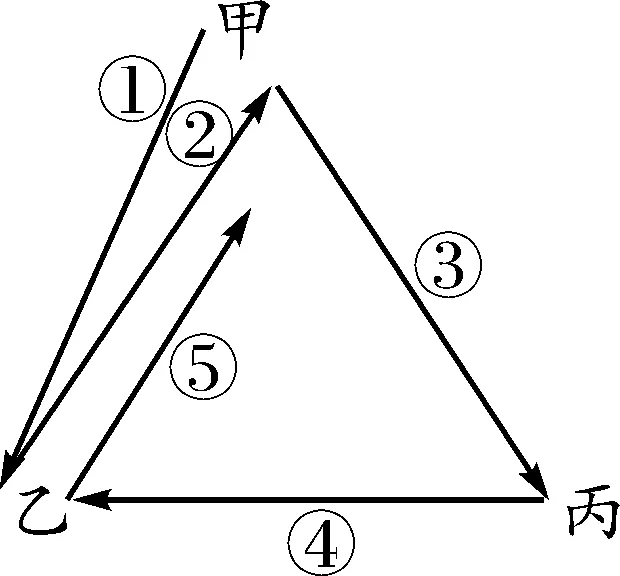
圖3-2

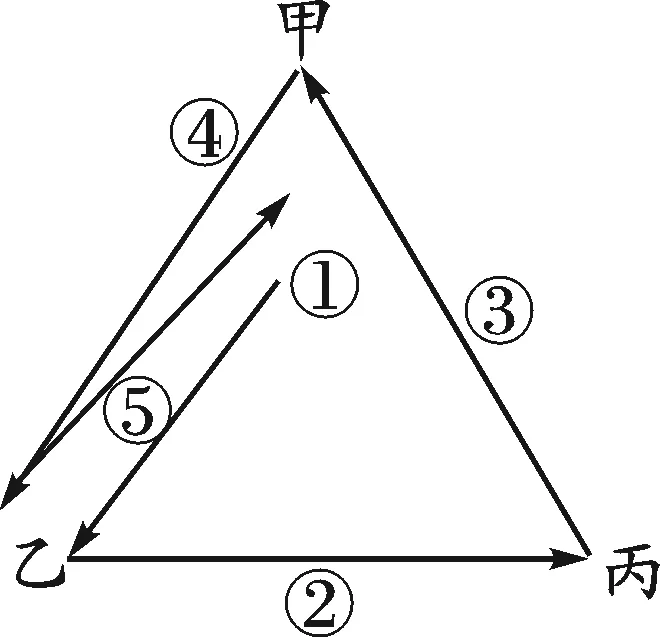
圖3-3

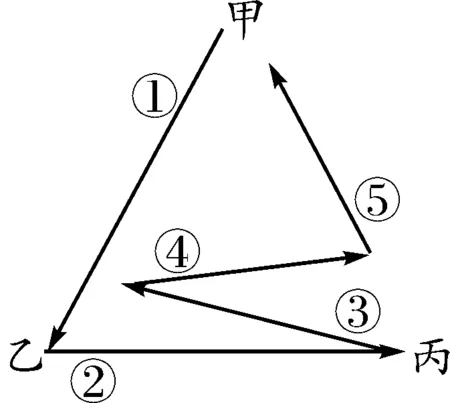
圖3-4

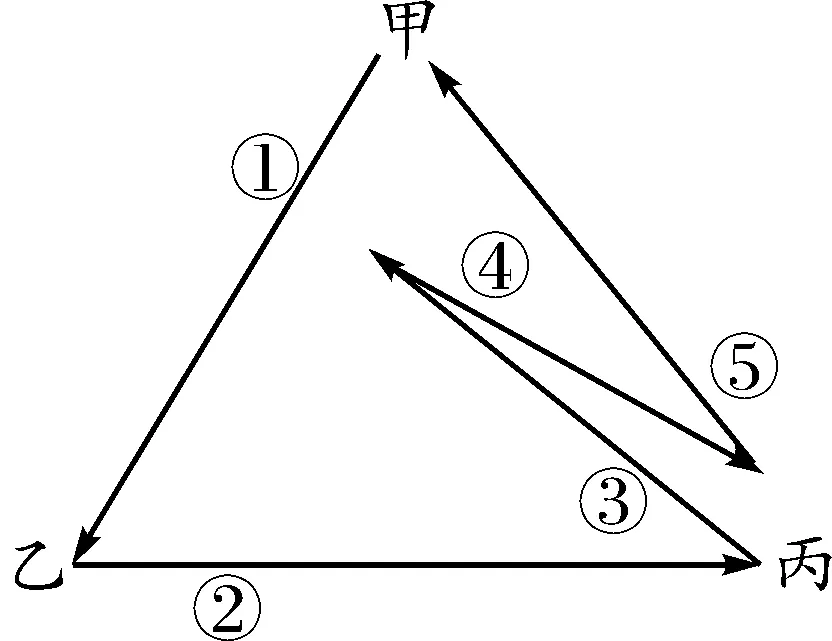
圖3-5

同理,甲若第一次傳球是給丙,則同樣有5種方式.故所有傳球方式共10種.

方法三：排列組合法

記“乙”與“丙”為“非甲”,則甲開始傳球,經過五次傳球,共有六個位置,如圖4所示.

圖4

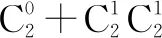
3 橫向聯系

排列組合問題的“實際背景”可能會多種多樣,但很多問題的本質是一樣的.關注和探究數學問題的本質,會大大促進數學思維能力、抽象概括能力以及解決問題能力的提高.因此,可利用某些典型問題,引領學生“適當”地進行橫向聯系,探究一些背景不同但本質相同的數學問題.

涂色問題在如圖5所示的六個方格里涂上紅、黃、藍三種顏色,要求相鄰兩個方格不同色,第1與第6兩格均為紅色,則涂色方法有多少種?(“第1與第6兩格均為紅色”與“球回到甲手中”本質相同.)

圖5

排數問題用1,2,3這三個數字排成六位整數,要求首位和末位排1,且任意相鄰的兩個數字不相同,則可以得到多少個不同的六位整數?(“首位和末位排1”與“球回到甲手中”本質相同.)

安排問題甲、乙、丙三人值班六天,每天一人值班,每個人值兩天班.其中,第一天和最后一天由甲值班,且相鄰兩天不能是同一人.則共有多少種不同的值班方式?

(“第一天和最后一天由甲值班”與“球回到甲手中”本質相同.)

對于上述問題,既可運用傳球問題中的解法來解決,又可根據此題的情境,生成貼近問題實際的解法.比如涂色問題,可有如下解法:

綜上可知,共有4+4+2=10種涂色方案.

其他問題,本質相同,就不做詳細解答了.

點評：上述給出的幾類問題中,有的問題可引導學生編制.這樣做不只是為了解幾個題,更重要的是讓學生通過這個過程,利用不同的背景進一步認識數學知識和數學思想方法的本質,提高數學思維能力、抽象概括能力以及解決問題的能力.

當然，在科研上光是“異想天開”是萬萬不行的。“異想天開”只是提供一個設想，而設想只是對問題的一個超前、大膽的預測，必須靠實事求是的科學態度和嚴謹的科學手段加以證明。實現創新突破的覃重軍也一再強調自己的“大膽猜想”，是經過了一系列嚴謹的科學實驗才最終得以成功實現的。

4 縱向拓展

上述傳球問題中只有3人,傳球也只有5次,還應根據學生的實際情況,引領學生將問題“逐步”推廣到一般情況,首先將“5次”傳球推廣到“n次”傳球.

拓展問題1甲、乙、丙三人開始傳球,由甲開始發球,并作為第一次傳球,經過n次傳球后,球仍回到甲手中,則不同的傳球方式共有多少種?

解析：設經過n次傳球后,球在甲手中的不同方法有an種,不在甲手中的方法有bn種.

顯然a1=0 , 并且an+bn=2n.

經過n次傳球后,球在甲手中,此時有an種方法.這說明第n-1次傳球后球沒在甲手中,此時有bn-1種方法,再從不在甲手中傳到甲手中只有一種途徑,即1種方法.

所以bn-1×1=an,即an=bn-1.

又因為an-1+bn-1=2n-1,所以an+an-1=2n-1.

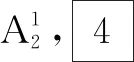
又a1=0 ,則問題轉化為求數列的通項公式.

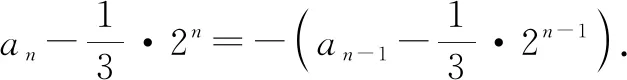
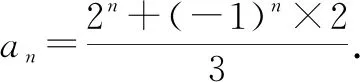
再把問題中的“3人”推廣到“m人”,就可把問題縱向推廣到更為一般的情況.

拓展問題2有m個人做傳球游戲,每個人可將球傳給任何一人,由甲開始發球,并作為第一次傳球,經過n次傳球后,球仍回到甲手中,則不同的傳球方式共有多少種?

解析：設經過n次傳球后,球在甲手中的不同方法有an種,不在甲手中的方法有bn種.

顯然a1=0 , 并且an+bn=(m-1)n.

經過n次傳球后,球在甲手中,此時有an種方法.這說明第n-1次傳球后球沒在甲手中,此時有bn-1種方法,再從不在甲手中傳到甲手中只有一種途徑,即1種方法.

所以bn-1×1=an,即an=bn-1.

又因為an-1+bn-1=(m-1)n-1,所以

an+an-1=(m-1)n-1.

又a1=0,則問題轉化為求數列的通項公式.

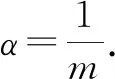
通過對三人傳球問題的橫向和縱向的思考和探究,既初步認識到了此類數學問題的本質,又感受到了數學知識之間的廣泛聯系.這對學習數學知識和解決數學問題有較好的啟發作用,同時讓學生進一步認識到——對待數學“問題”不能只是孤立地去解決,而應該用“聯系”和“運動”的眼光去研究它.退,能得到問題的“本源”;進,可拓展出其“一般性”,從而通過“追根求源”或“橫縱拓展”的探究活動,來體現思維過程和思想方法的“全景”.從這樣的過程中方可體悟出數學的真諦,從而進入神奇的數學世界中——聽數與式奏響的神奇韻律,看圖與形編織的美麗彩虹.