基于滑移線場理論的概率邊坡設計

韓非,胡超

(1.中航勘察設計研究院有限公司,北京 100098;2.四川輕化工大學土木工程學院,自貢 643000)

邊坡破壞(滑坡)是常見的自然災害之一,頻繁地導致人員、財產損失以及生態環境的破壞[1-3]。邊坡穩定性評價是防災減災工作的關鍵,為邊坡設計和治理提供了定量依據。近年來,基于概率論的可靠度分析方法越來越受到學術界的關注[4-6]。該方法將強度參數視為隨機變量,綜合考慮了強度參數的不確定性對邊坡穩定性的影響,不僅能給出定量的評價指標(安全系數)還可以給出定性評價指標(可靠度指標β和失效概率Pf),為工程設計人員提供了更多有益參考。然而,可靠度分析方法的計算效率一直是推動其在實際工程中應用的重要阻礙[7-8]。

邊坡可靠度分析方法是在概率論的框架下,利用傳統的邊坡穩定性分析方法確定失效域范圍,計算功能函數在失效域上的概率積分[9-11]。當前可靠度分析主要有解析法,近似法[如FORM(first-order reliability method)、SORM(second-order reliability method)和PEM(point estimate method)等],采樣法[如MCS(Monte Carlo simulation)、LHS(Latin hypercube sampling)和SS(subset simulation)等]以及響應面法等。采用不同的可靠度分析方法,需要結合相適應的邊坡穩定性分析方法,如限平衡法的可靠度分析方法[12-14]和數值模擬方法[15-17]。極限平衡法需要假定一定數量的潛在滑動面,然后確定失效概率最大的滑動面,這無疑是個非常艱巨的計算工作[18-19]。數值模擬方法能考慮巖土材料的應力-應變關系,不需要搜索潛在滑動面[20-22],因此該方法具有非常好的潛力。然而,數值模擬技術通過將問題域離散為一定數量的計算單元來求解偏微分方程,這就導致其計算量特別巨大,這種情況對于三維邊坡穩定性問題尤為明顯。

邊坡可靠度設計通常已知目標失效概率,而需要確定擬設計的坡角和坡高[23-24]。近年來,基于FORM逆可靠度法在邊坡設計中得到了越來越多的關注。蔣水華等[23]基于一階逆可靠度方法提出了能考慮土體參數空間變異性的坡角設計方法,該方法可以在少量試驗數據條件下獲得切合工程實際的邊坡設計方案,為坡角設計提供了一條新的有效途徑。蘇永華等[25]采用響應面方法對邊坡穩定性系數隱式表達式進行近似處理,并與基于FORM逆可靠度算法相結合,構建出一種具有可靠度與穩定性系數雙重控制指標的工程邊坡設計新方法。基于FORM逆可靠度方法把坡角和坡高考慮為隨機變量,通過求解目標失效概率或者可靠度指標,來獲得設計坡角和坡高。然而根據FORM法原理[26-27],計算得到的坡角和坡高只是概率空間空中到原點距離最近的設計點,由于考慮了土體參數的不確定性,在該點的坡角和坡高可能并不是全局最小的坡角和坡高,這就使得設計的邊坡可能并不經濟。此外,在逆可靠度方法的求解過程中,坡角和坡高的改變會導致計算模型幾何形狀發生變化,但是已有的研究并沒有介紹其實現的具體細節。這主要是由于當前采用的邊坡穩定性軟件大多是屬于第三方商業軟件,實際使用很大程度上受限于軟件提供的接口和功能等。

滑移線場理論避免了對任意滑動面的假設,并在給定的邊界應力下產生同時滿足平衡和塑性屈服的應力場。Jeldes等[28]將應用于邊坡穩定性分析中,并提出了臨界坡度的概念,基于該概念可判定邊坡的穩定狀態。Nandi等[29]基于改進的擬動力方法,推廣了滑移線場理論,使其能考慮地震對邊坡穩定性的影響,有效地考慮了土體的動力特性,如阻尼比和頻率效應。然而,基于滑移線場理論的邊坡可靠度分析方法研究鮮有報道[30]。

綜上所述,為了推進基于可靠度的邊坡優化設計方法的進一步發展,提出了一個基于滑移線場概率邊坡優化設計方法。該方法擬采用更加高效的擬蒙特卡羅模擬(quasi-Monte Carlo simulation,QMCS)來確定邊坡的失效概率,而在每次模擬過程中采用滑移線場理論來分析邊坡的穩定性。為了減少計算時間,在所提方法中一個簡單而有效地二分搜索方法用來計算目標失效概率的坡角。最后,通過案例研究論證所提方法的有效性。該方法可為基于可靠度邊坡設計提供新的技術手段。

1 基于滑移線理論的邊坡穩定性分析

1.1 滑移線理論

基于Mohr-Coulomb強度準則,邊坡土體中的任意一點應力狀態可表示為

σx=σ(1+sinφcos2θ)-ccotφ

(1)

σy=σ(1-sinφcos2θ)-ccotφ

(2)

τxy=σsinφsin2θ

(3)

式中:σx和σy分別為x和y向的正應力;τxy為xy平面內的剪應力;σ為與應力狀態有關的特征應力;c為黏聚力;φ為內摩擦角;θ為最大主應力和x軸的夾角。

在平面應變條件下,均值各向同性土體的平衡微分方程為

(4)

(5)

式(5)中:γ為土的重度。

將式(1)～式(3)代入式(4)和式(5),可得

(6)

(7)

方程(6)和(7)為雙曲線型方程組,存在兩簇滑移線(α簇和β簇,如圖1所示),可分別表示為

圖1 典型的滑移線場示意圖Fig.1 A typical net of characteristic lines

(8)

式(8)中:2μ為α簇和β簇滑移線之間的夾角,且有μ=π/4-φ/2,其中φ為內摩擦角。

(9)

滑移線上每一個點可以由x、y、θ和σ惟一確定。

Mα(xα,yα,θα,σα)為滑移線α簇上的一點,Mβ(xβ,yβ,θβ,σβ)為滑移線β簇上的一點。

(10)

(11)

式中:xα和xβ分別為Mα和Mβ點的x向坐標;yα和yβ分別為Mα和Mβ點的y向坐標;θα和θβ分別為在Mα和Mβ點處最大主應力和x軸的夾角;σα和σβ分別為在Mα和Mβ點處的特征應力。

為了計算邊坡的初始應力狀態,在邊坡頂部的點Mα和Mβ可通過式(12)進行確定。

(12)

式(12)中:Δx為坡頂的計算步長;ω為坡角;H為邊坡高度;P為作用在坡頂的荷載。

當邊坡頂部沒有外部荷載P時,或者外部荷載P小于式(13)給出的值時,P由式(13)進行確定,即

(13)

M(x,y,θ,σ)是滑移線α簇和β簇的交點,它可以由Mα和Mβ確定,x、y、θ和σ可分別表示為

(14)

(15)

θ=(σβ-σα)+2(σβθβ+σαθα)tanφ+

γ[(yα-yβ)+(2x-xα-xβ)tanφ]×

[2(σβ+σα)tanφ]-1

(16)

(17)

對于臨界邊坡線的點應滿足:

(18)

因此,對于已知的分別位于臨界邊坡線和滑移線β簇上的點Mb(xb,yb,θb,σb)和Mc(xc,yc,θc,σc),依據差分法,其交點Mij(xij,yij,θij,σij)可表示為

(19)

(20)

式中:xb和xc分別為Mb和Mc點的x向坐標;yb和yc分別為Mb和Mc點的y向坐標;θb和θc分別為在Mb和Mc點處最大主應力和x軸的夾角;σb和σc分別為在Mb和Mc點處的特征應力;xij為Mij點的x向坐標;yij為Mij點的y向坐標;θij為在Mij點處最大主應力和x軸的夾角;σij為在Mij點處的特征應力。

進一步結合式(16)和式(17),則交點Mij(xij,yij,θij,σij)可通過式(21)～式(24)計算得到。

xij=xbtan(θb-μ)-xctan(θc+μ)-

(yc-yb)[tanθb-tan(θc+μ)]-1

(21)

(22)

θij=(σc-σb)+2(σcθc+σbθb)tanφ+

γ[(yb-yc)+(2xij-xb-xc)tanφ]×

[2(σc+σb)tanφ]-1

(23)

(24)

在邊坡頂點O處,θb和σb可由式(25)、式(26)確定。

(25)

(26)

1.2 破壞準則及安全系數

前文已給出了基于滑移線場理論的邊坡穩定性分析方法,然而對于如何判定滑坡的極限狀態仍需要進一步闡述。如果已知γ、c、φ、ω和H,基于前述的滑移線場理論可以計算得到滑坡的滑移線,計算過程直至臨界邊坡線上的最低點的y*坐標值小于0截止(圖1)。由Jeldes等[28]提出的臨界坡度的概念可知,當臨界邊坡線通過坡腳的點時,也就是邊坡處于極限平衡狀態,如圖2中曲線b所示;當臨界邊坡線處于坡腳右邊時,滑坡處于穩定狀態,如圖2中曲線c所示;當臨界邊坡線處于坡腳左邊時,滑坡處于不穩定狀態,如圖2中曲線a所示。由圖2可知,當滑坡處于穩定時,計算過程應直至臨界邊坡線上的最低點的y*坐標值小于0;而當滑坡處于不穩定狀態時,臨界邊坡線處于坡腳左邊,因此計算過程應直至臨界邊坡線上的最低點的x*坐標處于等效坡面左側時,計算即可停止,從而減小不必要的計算(圖1)。

圖2 滑移線法確定的臨界邊坡線Fig.2 Determination of the critical slope contour by slip line field theory

基于臨界坡度的概念并結合傳統的強度折減法,通過不斷折減邊坡強度參數使得臨界邊坡線通過坡腳,即可獲得邊坡的安全系數。基于強度折減概念,土體強度參數可以采用式(27)進行折減。

(27)

式(27)中:R為折減因子;cr為折減后的黏聚力;φr為折減后的內摩擦角。

當邊坡處于極限平衡狀態時,有安全系數Fs=R。

2 基于概率的邊坡設計

2.1 擬蒙特卡洛模擬

QMCS是一種非常有效的基于抽樣的可靠性分析方法。計算效率高于蒙特卡羅模擬(MCS),平均收斂速度為O(N-1)[31]。QMCS在概念上類似于MCS,不同之處在于其使用低偏差序列樣本而不是偽隨機數。序列樣本是通過低偏差采樣(LDS)生成,并且比MCS中的偽隨機數生成的序列樣本更均勻[32]。Halton序列是常用的LDS采樣方法[33],采用Halton數列來估計邊坡的失效概率。

擬蒙特卡洛模擬的計算過程可分為3個步驟:首先,依據xi的概率分布生成N個隨機樣本;然后,將每個隨機樣本輸入到功能函數中計算對應的值。最后,統計失效樣本的數量,并采用式(28)來確定邊坡的失效概率Pf。

(28)

式(28)中:xi為第i個樣本;I(·)為指標函數,如果g(xi)≤0,則I[g(xi)]=1,否則I[g(xi)]=0。采用滑移線場理論分析邊坡穩定性時,如果g(xi)≤0時,即對應的是圖2中曲線a和曲線b情況;如果g(x)>0時,即對應的是圖2中曲線c情況。由式(28)可知,失效概率Pf的精度與樣本數量直接相關。為了保證計算精度以及計算效率,采用Pf的變異系數COVPf來估計樣本數量。

(29)

2.2 設計邊坡概率估計

圖3 不同坡角、坡高邊坡的安全系數Fig.3 Safety factor of slopes under different slope angles and slopes

(30)

圖4 計算流程圖Fig.4 Flowchart of the proposed method

為了實現所提邊坡設計方法,基于Python平臺編制了相應的計算程序。計算程序包括3個腳本文件Main.py、Slip_line_Slope.py、Cal_Pf.py以及Cal_Fs.py。Main.py腳本用于設置初始參數,展示最終計算結果;Slip_line_Slope.py腳本用于分析邊坡穩定性;Cal_Pf.py腳本用于計算邊坡失效概率;Cal_Fs.py腳本用于計算邊坡安全系數。

3 算例研究

表1 土體剪切強度參數Table 1 Shear strength parameters of soils

圖5 設計邊坡橫截面圖Fig.5 Cross section of design slope

3.1 邊坡參數統計特征

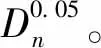
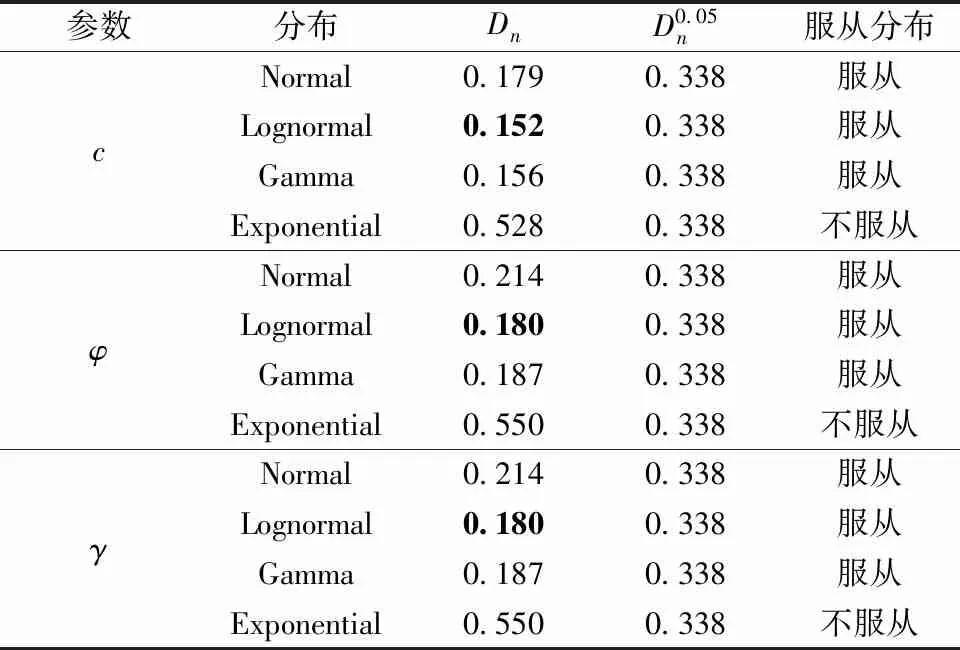
表2 剪切強度參數分布類型驗證(α=0.05)Table 2 Verification of probabilistic distribution of shear strength parameters(α=0.05)

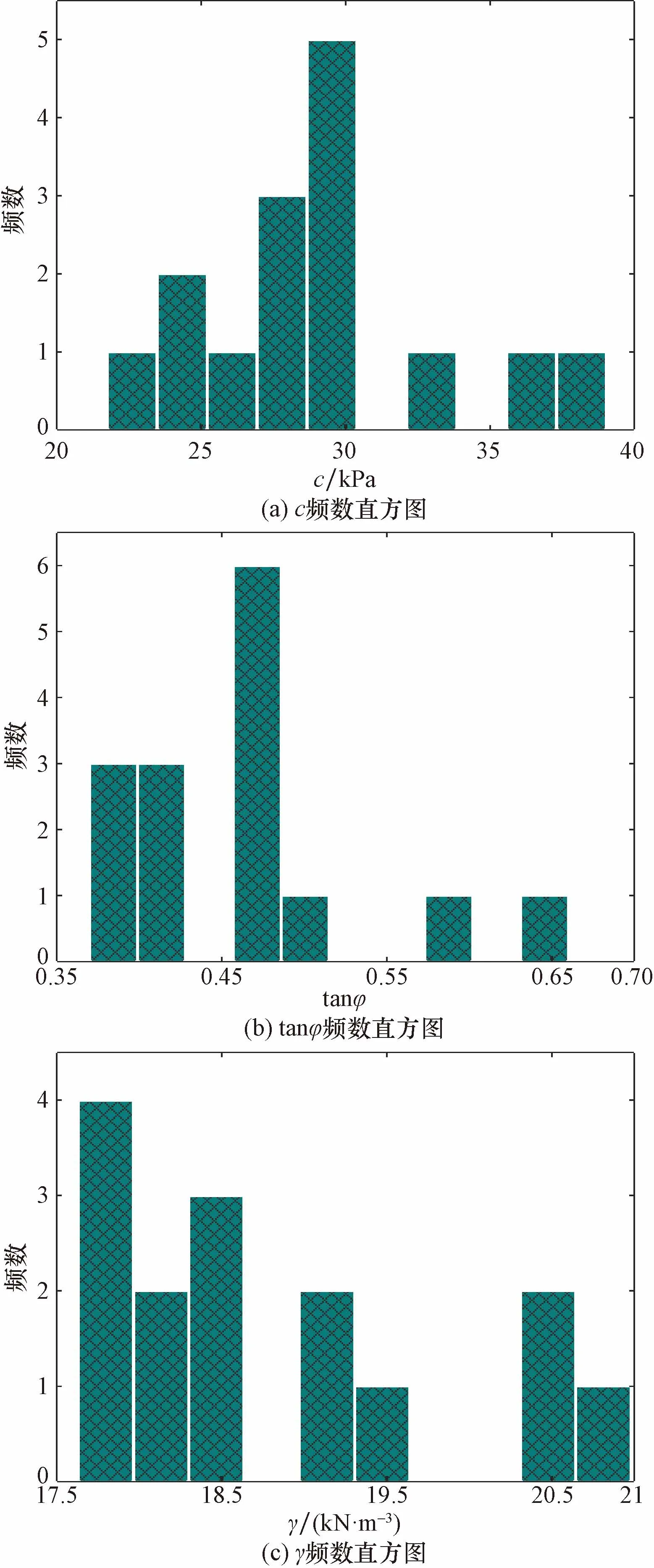
圖6 強度參數頻數直方圖Fig.6 Histogram of shear strength parameters

相關系數ρ是隨機場的重要參數,描述兩個隨機變量的聯合分布結構。對于服從Lognormal分布的黏聚力和內摩擦角,在不同相關系數下,基于蒙特卡洛模擬生成的樣本如圖7所示。圖7表明盡管黏聚力和內摩擦角都具有相同邊緣分布,但聯合分布是不同的。因此,有必要研究隨機場的相關性對隨機分析結果的影響。采用Spearman法確定了黏聚力和內摩擦角的相關系數ρc,φ=-0.13。

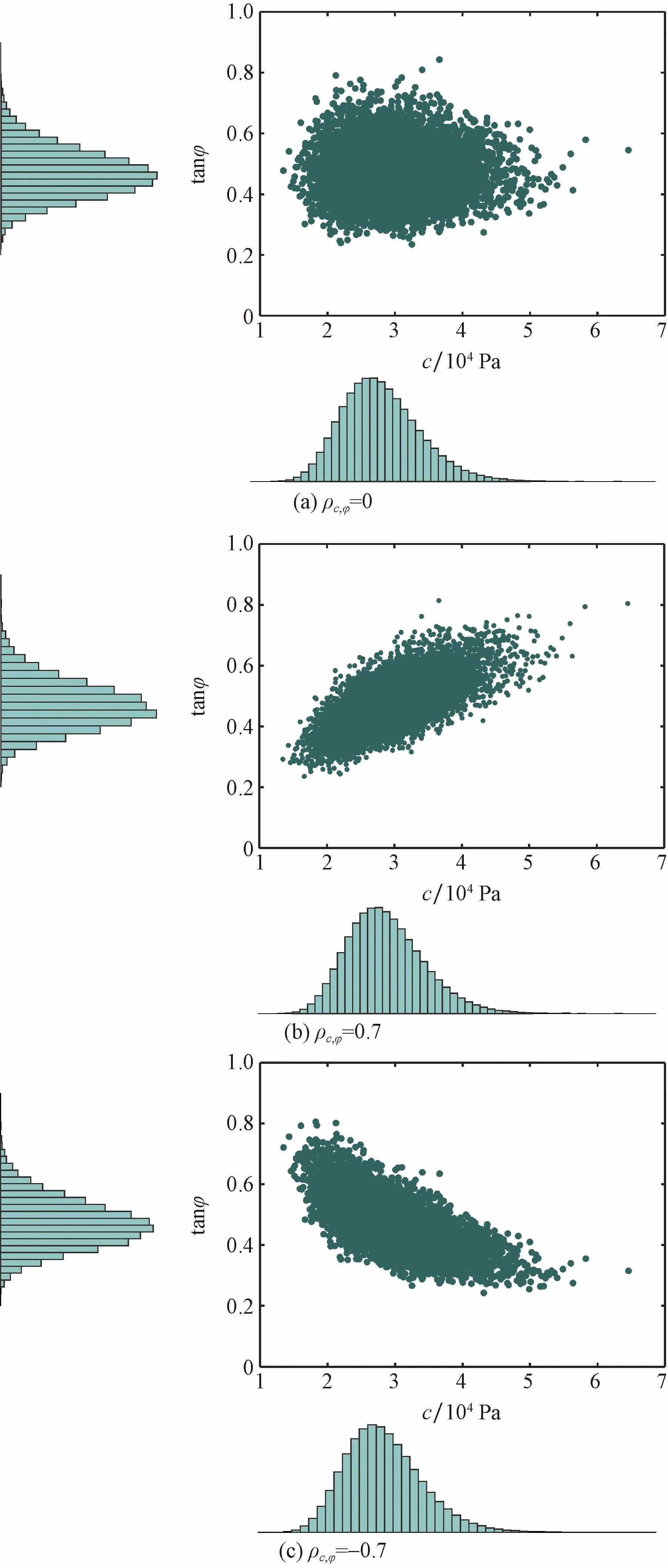
圖7 不同互相關系數下c和φ的聯合概率分布Fig.7 Joint probability distribution of c and φ under different cross-correlation coefficients

為了驗證基于滑移線場理論邊坡穩定性分析的有效性,以及自編腳本的可靠性。在邊坡未開挖時采用土體參數的平均值,計算得到的邊坡安全系數為1.27,該計算結果與GEOSTUDIO軟件采用Morgenstern-Price法和Spencer法計算得到的1.288結果相近。為了從分驗證基于滑移線場理論邊坡穩定性分析的有效性,計算了在不同坡角下的邊坡安全系數,計算結果如表3所示。可以看出,本文計算結果與GEOSTUDIO軟件計算結果幾乎一致。

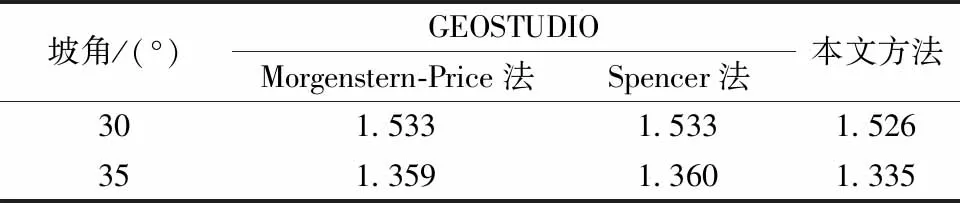
表3 不同方法計算的安全系數對比Table 3 Comparison of safety factors calculated by different methods

在邊坡未開挖時采用擬蒙特卡洛模擬,計算得到的邊坡安全系數的平均值為1.27,失效概率為3.56×10-2。盡管安全系數的平均值表明邊坡在為開挖狀態下邊坡處于穩定狀態,但是此時邊坡的坡角較大,邊坡失效概率并不滿足目標失效概率要求,因此需進行邊坡挖開處理。

3.2 概率邊坡優化設計

圖8 計算過程Fig.8 Calculation process

為了驗證所提方法的有效性,在現有的土體參數以及計算得到的坡角值的基礎上,利用直接蒙特卡洛模擬(MCS),重新計算的邊坡失效概率分別為1×10-2、1×10-3和1×10-4,計算結果與目標失效概率一致,驗證了所提方法的有效性。

4 參數研究

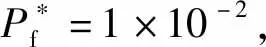
由圖9(a)、圖9(b)可知,隨著黏聚力和內摩擦角平均值的增加設計坡角將逐步增大,而隨著黏聚力和內摩擦角標準差的增加設計坡角逐步減小。隨著黏聚力和內摩擦角平均值的增加,土體抗剪強度逐步增大,邊坡穩定性逐步增加,因此設計坡角也隨之逐漸增大。當黏聚力和內摩擦角的標準差增加時,盡管黏聚力和摩擦角的平均值未發生變化,但是邊坡失效概率也隨之增大,因此要滿足目標失效概率的設計坡角也應減小。由圖9(c)可知,隨著重度平均值和標準差的增加設計坡角逐步增小。由圖9(d)可知,隨著相關系數的減小,設計坡角逐步增大。隨著相關系數的減小,黏聚力和內摩擦角逐步呈負相關性,由圖7(c)可知,此時在失效域范圍的隨機樣本數量越少,邊坡失效概率較小,因此在相對較大的設計坡角下即可滿足目標失效概率。

5 結論

將滑移線場理論應用于邊坡設計,提出了基于失效概率的邊坡設計新方法。新方法采用了二分搜索算法來求解滿足目標失效概率解,并且在每次搜索過程中使用了能更加快速收斂的擬蒙特卡洛模擬方法來計算邊坡失效概率。以一個實際邊坡為例進行了邊坡概率優化設計。得出如下主要結論。

(1)所提方法計算效率高,最多只需36.29 min就能得到滿足目標失效概率的結果。傳統的基于極限平衡法和數值模擬方法的邊坡穩定性分析,在搜索過程中邊坡的坡角和坡高會不斷變化,從而導致邊坡幾何模型的變化,這使得計算過程的模型重構工作十分復雜。所提出的邊坡概率優化設計方法可簡化這一問題的難度,提高了計算效率,為一般的隱式邊坡可靠度設計奠定基礎。

(2)參數研究表明,土體參數的平均值、標準差以及相關系數與設計坡角的規律,研究成果為基于概率論的邊坡優化設計提供了新的方法。

(3)僅將土體參數考慮為隨機變量,忽略了土體參數空間變異性,具有一定的局限性。如何將所提方法進一步推廣能更加全面的考慮土體參數的空間異性將是需要進一步研究的內容。