不同溫度下含裂紋壓氣機葉片的模態特征和振動特性分析

周震霆，賀 星，劉永葆

(海軍工程大學 動力工程學院, 湖北 武漢 430033)

0 引 言

壓氣機葉片是燃氣輪機運行過程中完成能量轉換的基本單元，也是燃氣輪機關鍵部件中出現故障的最典型部件之一。裂紋是壓氣機葉片出現故障的常見形式之一，裂紋的存在將會改變葉片的模態特征和振動特性。燃氣輪機壓氣機葉片工作環境惡劣，承受著離心載荷和氣動載荷等復雜載荷的影響，特別是高壓壓氣機，隨著壓比的升高，高壓壓氣機周圍氣流的溫度也不斷升高，同時燃燒室通過傳熱等方式也會導致高壓壓氣機溫度升高。在高溫的影響下，壓氣機葉片的材料和力學性能會發生變化，也會對壓氣機葉片的模態和振動特性產生影響。

壓氣機葉片可被看作懸臂梁，通過裂紋懸臂梁模型模擬含裂紋的壓氣機葉片。對于含裂紋梁的模態特征和振動特性，20 世紀便有人開始進行了研究，并發展至今[1-9]，可見研究含裂紋梁的模態特征和振動特性具有實際的工程意義。分析裂紋深度、裂紋位置、結構阻尼、剛度等因素對梁的模態特征和振動特性的影響，卻很少考慮溫度的影響[10-12]。然而在實際過程中，空氣流過各級葉片時，由于受到壓縮，壓力和溫度會逐級升高，位于后面級的壓氣機，溫度產生的影響很難忽略，尤其是在迫切渴求實時監測和在線診斷的今天。若想在燃氣輪機工作過程中得到壓氣機葉片的狀態信息，其所處工況的環境溫度應考慮在內。

本文通過含裂紋懸臂梁模型模擬含裂紋的壓氣機葉片，采用無質量扭轉彈簧等效代替裂紋。通過彈性模量引入溫度模塊，推導出不同溫度下含裂紋懸臂梁的模態特征方程，并通過梁的受迫彎曲振動方程，得到溫度影響下梁的振動特性曲線。

1 模型建立和模態分析

1.1 含裂紋懸臂梁模型建立

如圖1(a) 所示，建立一段長為L，寬為b，高為h的等截面矩形懸臂梁模擬裂紋葉片，并忽略裂紋尺寸隨溫度的變化。在該懸臂梁表面有一條深度為a的裂紋，該裂紋距離固定端的距離為R。

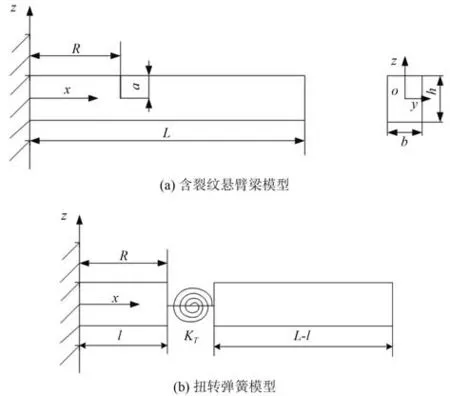
圖1 含裂紋葉片等效模型Fig. 1 xxxx

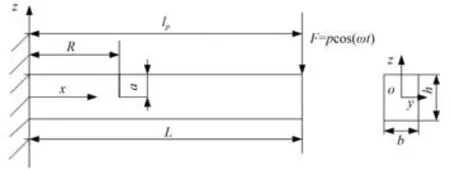
圖2 含裂紋懸臂梁模型Fig. 2 xxxx

如圖1（b）所示，該含裂紋懸臂梁可以等效成由1 條無質量扭轉彈簧連接的2 段無損彈性梁。對于該懸臂梁的彎曲振動，只考慮等效彈簧的剛度KT,該裂紋等效剛度的表達式為：

式中：L為懸臂梁的長度，η=l/L為裂紋的相對位置，ν為泊松比，ET為不同溫度下的彈性模量；r=a/h為相對裂紋深度。通過文獻[13] 得到材料TC11 的彈性模量如表1 所示。

表1 TC11 不同溫度下的彈性模量Tab. 1 xxxx

1.2 模態分析

圖1 為各向同性的含裂紋等截面均質懸臂梁，則梁的自由振動微分方程為：

式中：ρ為材料密度，ET為彈性模量，I為截面慣性矩，y(x,t)為梁的撓度，A為梁的截面面積。

假定有分離變量解存在，令y(x,t)=Y(x)T(t)，代入式（1）分離變量t可得：

Y(x)表示位移，A1,B1,C1,D1表示裂紋左側梁與邊界條件有關的未知參數，A2,B2,C2,D2表示裂紋右側梁與邊界條件有關的未知參數。

懸臂梁的邊界條件為：

固定端（x=0）的撓度和撓角

自由端（x=l）的彎矩和剪力為0：

假設裂紋所在位置為x=R，將裂紋等效成無質量扭轉彈簧，因此，裂紋處的連續條件為：

裂紋兩側撓度相等

裂紋兩側撓角變化關系：

裂紋兩側彎矩相等

裂紋兩側剪力相等

式中，KT為扭轉彈簧剛度。由梁的自由振動方程解和梁的邊界條件及彈簧連續條件，可得：

其中，矩陣S表達式為：

根據式（7）可得到k值，進而得到裂紋梁的固有頻率ωg，將得到的k值代入到位移方程中，可得到含裂紋梁的模態振型。

2 振動特性分析

2.1 建立呼吸式裂紋梁彎曲振動方程

在圖1（a）的基礎上，距懸臂梁固定端lp處引入大小為F的余弦激振力，激振頻率為ωJ。

忽略裂紋對懸臂梁振動的影響，橫向力激勵下梁的受迫彎曲振動方程為[14]：

式中：c為阻尼系數，p為橫向激勵力的幅值，lp為激勵力離固支端的距離，ωJ為外激勵頻率，δ為Dirac 函數，x為坐標，t為時間。

利用假設的裂紋梁橫向固有振動形式y(x,t)=Y(x)T(t)，根據懸臂梁的邊界條件，得到懸臂梁的振型函數為[15]：

將y(x,t)=Y(x)T(t)代入式（8）中，左右兩端同時乘U(x)，并在0～L上積分可得：

其中：

式中：m*為廣義質量；c*為廣義阻尼；k*為無裂紋梁的廣義剛度，即無損梁剛度；F*為廣義力。其中k*用呼吸式裂紋剛度kbr替代，從而得到呼吸式裂紋梁的彎曲振動方程。

對于呼吸式裂紋剛度kbr，劉文光等[14]提出：

其中：

式中，ko為張開式裂紋梁模型。當ωt=2nπ (n=1,2,…)時，裂紋完全閉合，此時呼吸梁模型等效為閉合梁模型，即kbr=k*；當ωt= (2n-1)π，(n=1,2,…)時，裂紋完全張開，此時呼吸梁模型等效為張開梁模型，即kbr=ko。

將式（10）的k*用式（16）中的呼吸式裂紋剛度kbr替代，從而得到呼吸式裂紋梁的彎曲振動方程：

2.2 振動特性分析

由式（13）可知，懸臂梁的廣義剛度與彈性模量具有一定的關系，因此可知呼吸式裂紋剛度與彈性模量也具有關系。溫度的變化通過對彈性模量的影響，導致呼吸式裂紋剛度發生變化，進而會對梁的振動位移響應造成影響。通過對梁的振動位移及其他振動特性與溫度的變化之間的規律進行分析，得出相關結論。

3 結果與討論

從圖1 所示懸臂梁為例模擬含裂紋葉片，假設葉片的幾何尺寸為：長度L= 0.09 m，寬度b= 0.055 m，高度h= 0.006 m；材料參數為：密度ρ= 4 480 kg.m-3，泊松比v= 0.33，阻尼比ξ= 0.05，彈性模量ET隨溫度發生變化。

3.1 環境溫度對裂紋梁模態特征的影響

結合假設的含裂紋葉片的幾何尺寸，取裂紋的相對位置為R/L= 1/9，相對深度為環境溫度的變化范圍為T∈{20℃ 100℃ 200℃ 300℃400℃ 500℃ 600℃ }。通過數值計算得到環境溫度和不同相對裂紋深度與含裂紋梁的第1 階固有頻率之間的關系如圖3 所示。

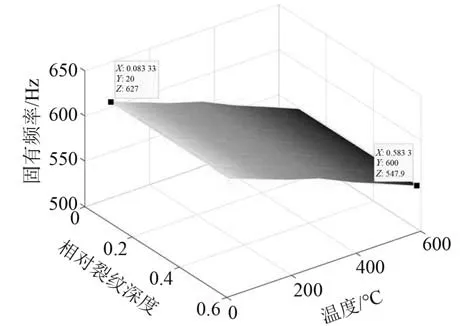
圖3 固有頻率對環境溫度變化曲線Fig. 3 xxxx

可以看出，在懸臂梁裂紋位置和深度一定的情況下，當環境溫度不斷增大時，懸臂梁的固有頻率不斷減少。通過比較，可知懸臂梁在環境溫度為600℃下的固有頻率比在20℃下的降低70 Hz 左右，大約為懸臂梁固有頻率的12%左右。由此可見，環境溫度對懸臂梁固有頻率具有一定的影響。而當溫度不變的情況下，梁的相對裂紋深度越大，固有頻率越低。同時也可以看出，當梁的相對裂紋位置不變的情況下，環境溫度對梁的一階固有頻率的影響明顯比相對裂紋深度大。

3.2 環境溫度對裂紋梁振動特性的影響

在假設的含裂紋葉片幾何尺寸以及材料參數基礎上，裂紋位置R= 0.01 m，裂紋深度為a= 0.000 5 m，引入外部簡諧激振力F=pcos(ωt)，其中激振力幅值為100 N，環境溫度的變化為T∈{20℃ 300℃ 600℃} ，使梁分別在400 Hz、固有頻率及4 000 Hz 下振動，通過數值計算得到環境溫度與含裂紋梁的振動特性之間的關系如圖4～圖6 所示。

圖4 400 Hz 頻率下振動特性圖Fig. 4 xxxx

由圖4 和圖5 中的位移響應圖可以看出，在選取的低頻和固有頻率作用下，溫度越高，梁的振動幅值越大。這是因為隨著溫度的升高，梁的剛度和阻尼會出現減小的情況，在相同激振力幅值的影響下，剛度和阻尼越小，梁的位移響應越大。從圖4 和圖5 的相圖也可以看到相關現象，反應出選取的呼吸式裂紋剛度所作用的效果。同時，從圖5（b）可以看到在共振情況下阻尼產生明顯的響應滯后效應。

圖5 固有頻率下振動特性圖Fig. 5 xxxx

在選取的高頻作用下，為溫度越高，梁的振動幅值越大，與低頻作用下的現象不同，如圖6 所示。隨著溫度的升高，梁的剛度和阻尼減小，梁的位移響應增大。在相同階數彎曲頻率下，隨著溫度的升高，梁的固有頻率下降，且下降幅度較大。在每一階頻率附近都存在一個幅值峰，各階頻率構成了連續的幅值峰。當梁處于300℃和600℃時，4 000 Hz 可能位于該溫度下某一高階幅值峰的中段，而位于20℃下某一高階與臨近低階間的谷底。

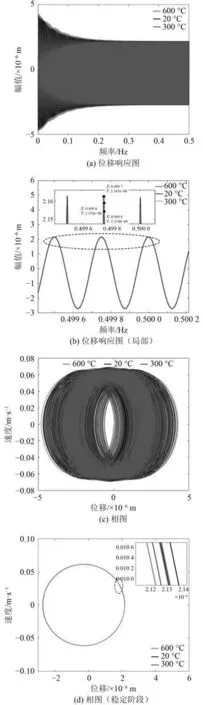
圖6 4 000 Hz 下振動特性圖Fig. 6 xxxx

4 結 語

本文通過含裂紋懸臂梁模擬含裂紋壓氣機葉片，選取無質量扭轉彈簧模擬裂紋，并引入呼吸式裂紋剛度模擬裂紋振動過程中的呼吸效應。通過彈性模量引入溫度模塊，研究環境溫度對含裂紋壓氣機葉片的一階固有頻率和振動響應之間的關系，得出以下結論：

1）環境溫度對梁的一階固有頻率具有一定的影響，隨著環境溫度的升高，梁的一階固有頻率下降，而且下降的幅度較裂紋深度帶來的影響更大。

2）在低頻及固有頻率激振力作用下，隨著環境溫度的升高，梁的位移響應越大，但在高頻激振力作用下，出現了不同的現象。這是所選激振頻率處于不同溫度下各階頻率的距離遠近導致的。

由此可見，環境溫度對葉片的模態特征和振動特性具有一定影響。若想在實際工作過程中實現實時監測和在線診斷，應選取合適的工作頻率，需要后續進行研究得到。