MPSK信號類內調制樣式識別研究

黃 剛

(中國電子科技集團公司第二十研究所,陜西 西安 710068)

0 引 言

調制樣式是不同通信體制信號的重要特征。在非合作通信中,信號的調制樣式識別是十分關鍵的技術。截取電磁波信號,分析識別信號的調制方式,估計信號的相關參量,為接收解調設備解析信號內容提供了重要的理論依據。隨著無線電技術飛速發展,不斷涌現出各種新型調制技術。多進制相移鍵控調制(MPSK)具備傳輸頻帶利用率高、抗干擾能力強等特點,被大量應用于衛星通信、遙控測量、電臺等多種無線通信系統。為了實現有限帶寬內傳輸容量擴大,MPSK調制技術從二進制相移鍵控(BPSK)發展到正交相移鍵控(QPSK)、八進制相移鍵控(8PSK)等高階相位數字調制。同時,為了使得調制波形具備更好的恒包絡特性,減小射頻功率器件的非線性造成的功率譜旁瓣增生效應,在QPSK基礎上又發展了偏移四相相移鍵控(OQPSK)、π/4-QPSK,它們具備了更小的相位跳變,使得信號包絡特性更好。因此,研究MPSK類內(BPSK、QPSK、OQPSK、π/4-QPSK、8PSK)信號調制樣式的識別具有重要的現實價值。

文獻[1]提出了根據不同調制信號的相位直方圖統計識別BPSK、QPSK、OQPSK信號調制樣式,但是該方法受噪聲干擾較大,識別不穩定。文獻[2]提出采用四階和六階累積量識別BPSK、QPSK、8PSK,但是OQPSK和QPSK、8PSK和π/4-QPSK的累積量相同,無法實現這幾種信號類內識別。文獻[3]提出基于差分星座進行多級聚類的方法識別π/4-QPSK和8PSK信號調制樣式。文獻[4]提出了一種基于信號的四階、八階累積量作為特征識別BPSK、QPSK、π/4-QPSK和8PSK調制信號,但是計算信號的八階累積量運算較為復雜。本文提出了一種基于信號四階累積量和差分星座最小環帶方差聯合特征識別BPSK、QPSK、OQPSK、π/4-QPSK和8PSK調制信號,該方法能夠較好地識別MPSK類內幾種信號,同時對于載波殘余相位不敏感,計算復雜度較低。

1 信號模型

本文假設接收信號已載波恢復和定時同步,其表示為:

(1)

式中:a(k)表示碼元序列,k=1,2,…,N,N表示碼元長度,a(k)∈{ej2π(m-1)/M,m=1,2,…,M},M表示調制相位進制,本文中對于BPSK、QPSK和8PSK,M取值分別為2,4,8;E表示信號的平均功率;Δθ為載波相位殘差;n(k)為均值為0,方差為N0的復高斯白噪聲。

OQPSK是在QPSK基礎上發展起來的,相位只在0°和±90° 3種相位之間跳變,因此OQPSK碼元可以表示為:

a(k)∈{ej2π(m-1)/4+Δφ,m=1,2,3,4,Δφ=0,±π/2}

(2)

對于π/4-QPSK,信號的相鄰碼元之間相位差為π/4,因此π/4-QPSK碼元信號可以表示為:

a(k)∈{ej2π(m-1)/4,m=1,2,3,4}

(3)

a(k+1)∈{ej2π(m-1)/4+π/4,m=1,2,3,4}

(4)

2 特征提取和分類識別

2.1 高階累積量

對于1個零均值的k階平穩隨機過程x(t),其k階累積量定義[5]為:

Ckx(f1,f2,…,fk-1)=Cum(x(t),x(t+f1),…,

x(t+fk-1))

(5)

式中:Cum(·)表示求累積量。

定義x(t)的p階混合矩[5]為:

Mpq=E{[xp-q(t)x*(t)q]}

(6)

因此,x(t)的二階、四階累積量[6]表示為:

(7)

根據式(5)～式(7),可知高斯白噪聲的二階以上的累積量恒定為0,因此計算BPSK、QPSK、OQPSK、π/4-QPSK和8PSK的四階累積量理論值如表1所示。

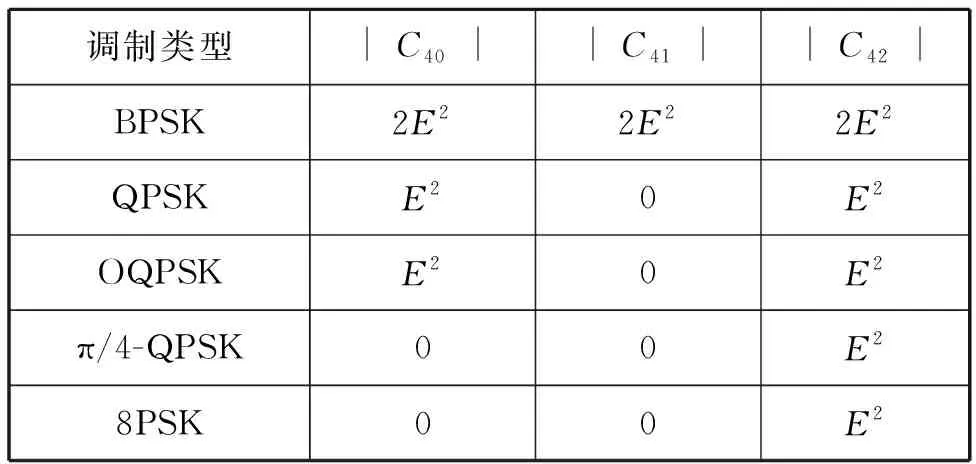
表1 四階累積量理論值

表中E表示接收信號的能量。

針對不同的調制樣式,結合表1,特征向量F的理論值為:

(8)

因此,利用特征向量F,采用最小歐式距離準則建立分類判決器,分類判決器表示為:

(9)

通過該分類判決器,可以將BPSK、QPSK、OQPSK、π/4-QPSK、8PSK分為三大類:BPSK、{QPSK、OQPSK}、{π/4-QPSK、8PSK}。

2.2 差分星座最小環帶模值方差

根據式(2)～式(4),可知QPSK和OQPSK、π/4-QPSK和8PSK星座分布相同。但是,事實上QPSK和OQPSK、π/4-QPSK和8PSK的相位跳變規律是不同的,因此QPSK和OQPSK、π/4-QPSK和8PSK信號差分運算后的星座圖分布是有差異的。對式(1)的信號進行差分運算,得到:

Δy(k)=y(k+1)-y(k)=

(10)

式中:Δn(k)表示均值為0、方差為2N0的復高斯白噪聲。

圖1～圖8為4種不同調制樣式的信號星座圖和差分重構星座圖。

圖1 QPSK調制星座圖

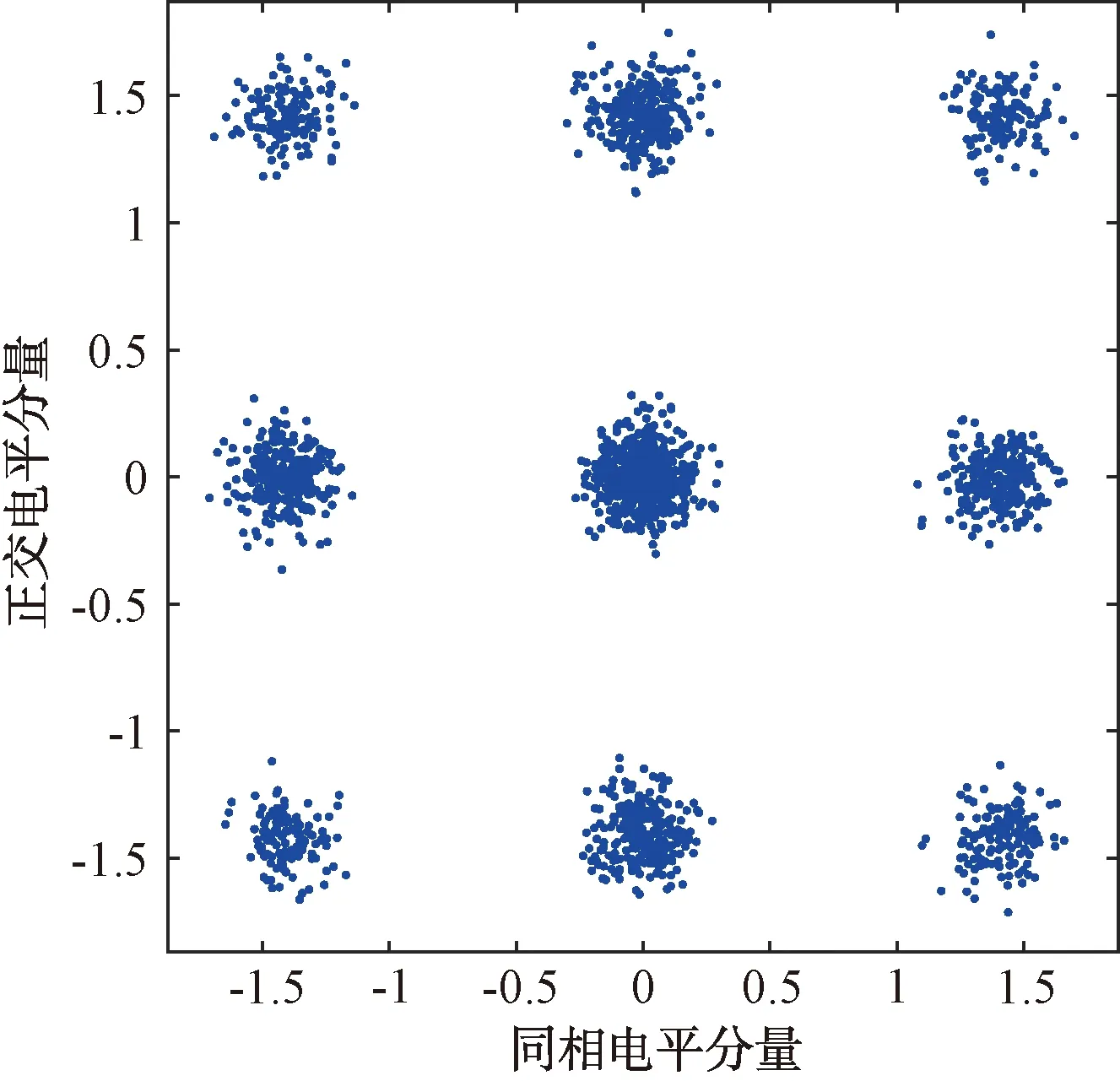
圖2 差分QPSK調制星座圖

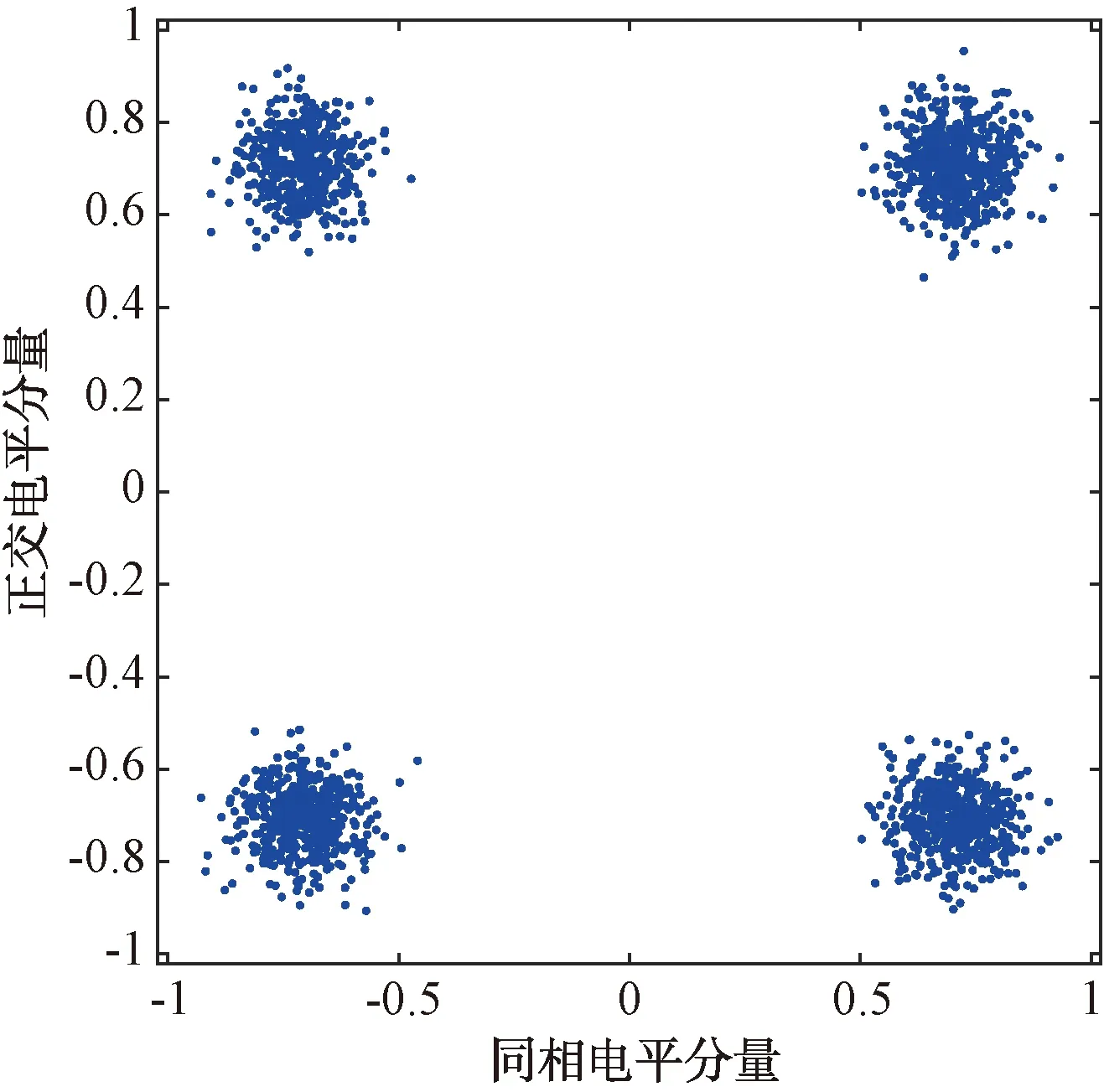
圖3 OQPSK調制星座圖

圖4 差分OQPSK調制星座圖

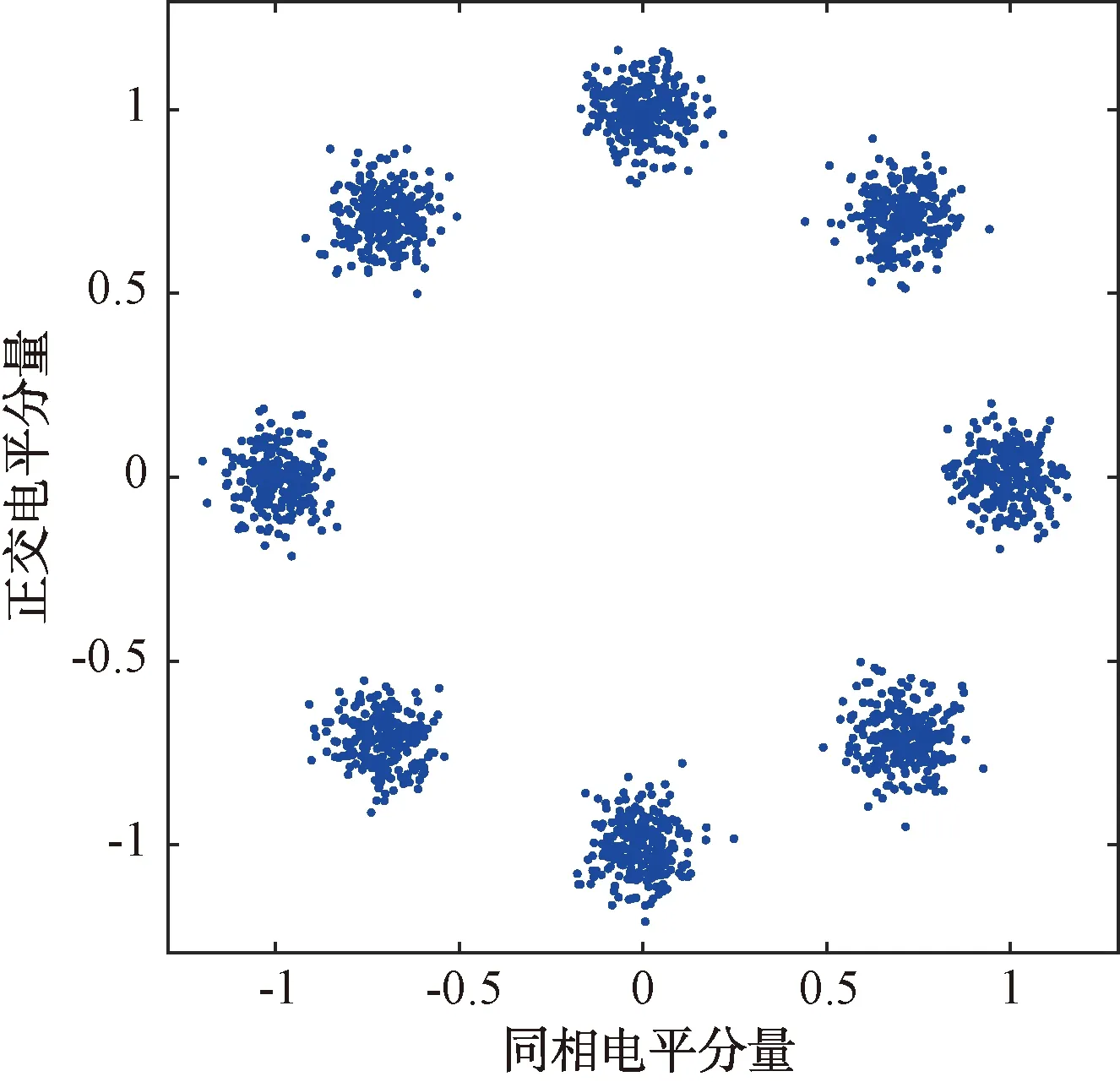
圖5 π/4-QPSK調制星座圖

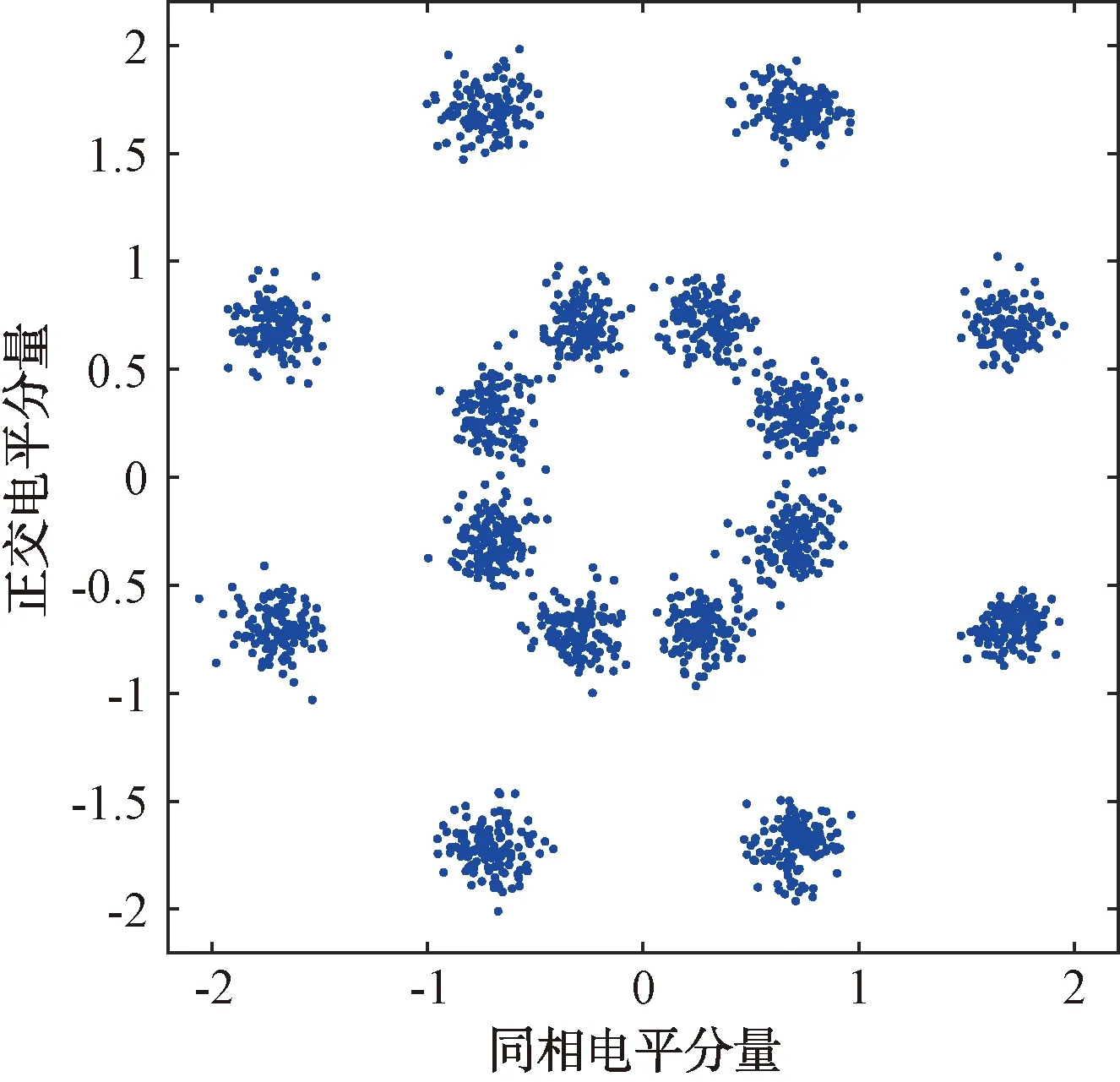
圖6 差分π/4-QPSK調制星座圖

圖7 PSK調制星座圖

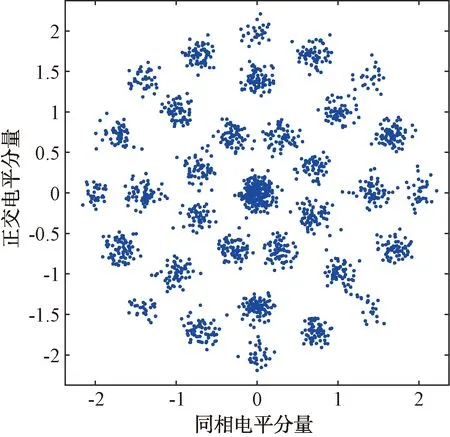
圖8 差分8PSK調制星座圖

根據式(2)、(3)、(4)、(10),差分星座分布規律如下:差分QPSK信號星座按照近似25%、50%、25%分布在內外3個環帶上。差分OQPSK信號星座按照近似50%、50%分布在內外2個環帶上。差分π/4-QPSK信號星座按照近似50%、50%分布在內外2個環帶上。差分8PSK信號星座按照近似12.5%、25%、25%、25%、12.5%分布在內外5個環帶上。如果星座點全部來自同一個環帶,則模值方差比較小。反之,不同環帶星座點的模值方差較大。已知距離星座圖中心點越遠的點,其模值分布越緊湊[7]。因此,越靠近星座圖的外環帶星座點越容易受噪聲等因素干擾導致環帶不清晰。針對QPSK、OQPSK、π/4-QPSK和8PSK信號,本文采用差分星座的最小環帶模值方差作為特征進行分類識別。

首先,計算差分信號瞬時歸一化幅值,表示為:

(11)

(12)

然后,瞬時歸一化幅值排序,表示為:

S(k)=sort(Y(k))

(13)

式中:sort(*)表示升序排列運算;k=1,…,N。

最后,計算截斷長度為L的S(k)方差,表示為:

Pr=var(S(k)),k=1,2,…,L

(14)

式中:var(*)表示方差運算;L≤N。

對于OQPSK,S(k)的前N/2數據來自最小環帶;對于QPSK,S(k)的前N/2數據肯定來自不同的環帶,因此方差必然偏大。同理,對于π/4-QPSK,S(k)的前N/2數據來自最小環帶;對于8PSK,S(k)的前N/2數據肯定來自不同的環帶,因此方差必然偏大。通過Pr和理論閾值比較,{QPSK、OQPSK}信號小于門限判定為OQPSK,否則為QPSK;{π/4-QPSK、8PSK}信號小于門限判定為π/4-QPSK,否則為8PSK。

對上述4種調制信號的星座點按照上述比例截斷,得到模值方差的理論值如表2所示。

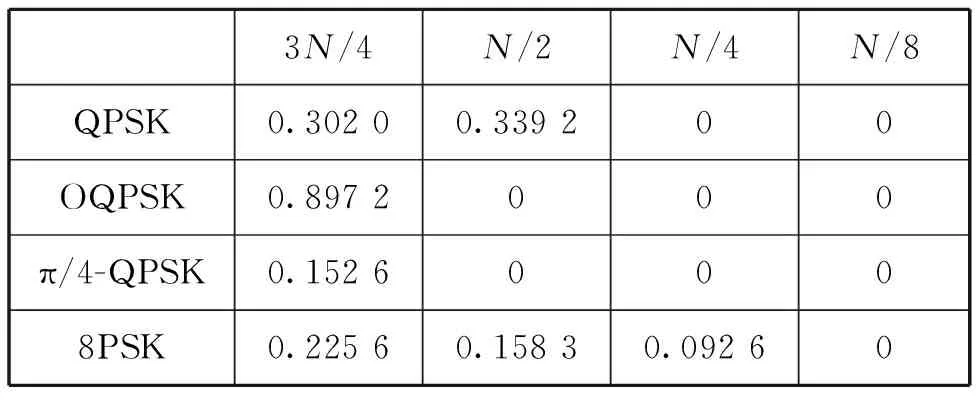
表2 各種信號不同截斷長度模值方差理論值

由于受噪聲、碼間干擾以及有限長度截斷等因素影響,實際應用中門限閾值稍微高于理論值。

2.3 分類識別流程

根據上述分析,BPSK、QPSK、OQPSK、π/4-QPSK、8PSK 5種調制信號的識別流程如下:

(2) 根據式(9)將調制信號分為三大類:BPSK、{QPSK、OQPSK}、{π/4-QPSK、8PSK}。

(3) 根據式(11)、(12)、(13)計算N點長度信號的升序瞬時歸一化幅值,截斷L=N/2計算結果,根據式(15)計算星座最小環帶模值方差特征f3。對于{QPSK、OQPSK}子類信號,如果方差小于設定門限h1,則判定為OQPSK;否則,判定為QPSK。對于{π/4-QPSK、8PSK}子類信號,如果方差小于設定門限h2,則判定為π/4-QPSK;否則,判定為8PSK。

3 仿真分析

針對提出的BPSK、QPSK、OQPSK、π/4-QPSK、8PSK調制信號樣式識別算法,本文采用MALTAB軟件進行算法性能仿真驗證。分別仿真了不同信號長度、不同信噪比和載波剩余相位下的信號調制樣式識別性能。

(1) 不同信號長度下算法識別性能

設定信噪比為10 dB,載波剩余相位殘差為0,信號長度N為400,600,800,1 000,1 200,1 400,1 600,1 800,2 000,2 200,判決門限h1=0.085,h2=0.05,每種信號2 000次識別,不同信號長度下算法的識別性能情況如圖9所示。根據圖9分析可知,隨著信號長度N的增加,調制信號的識別準確率逐漸增加。當信號長度N達到1 600,幾種調制信號識別率可以達到100%。

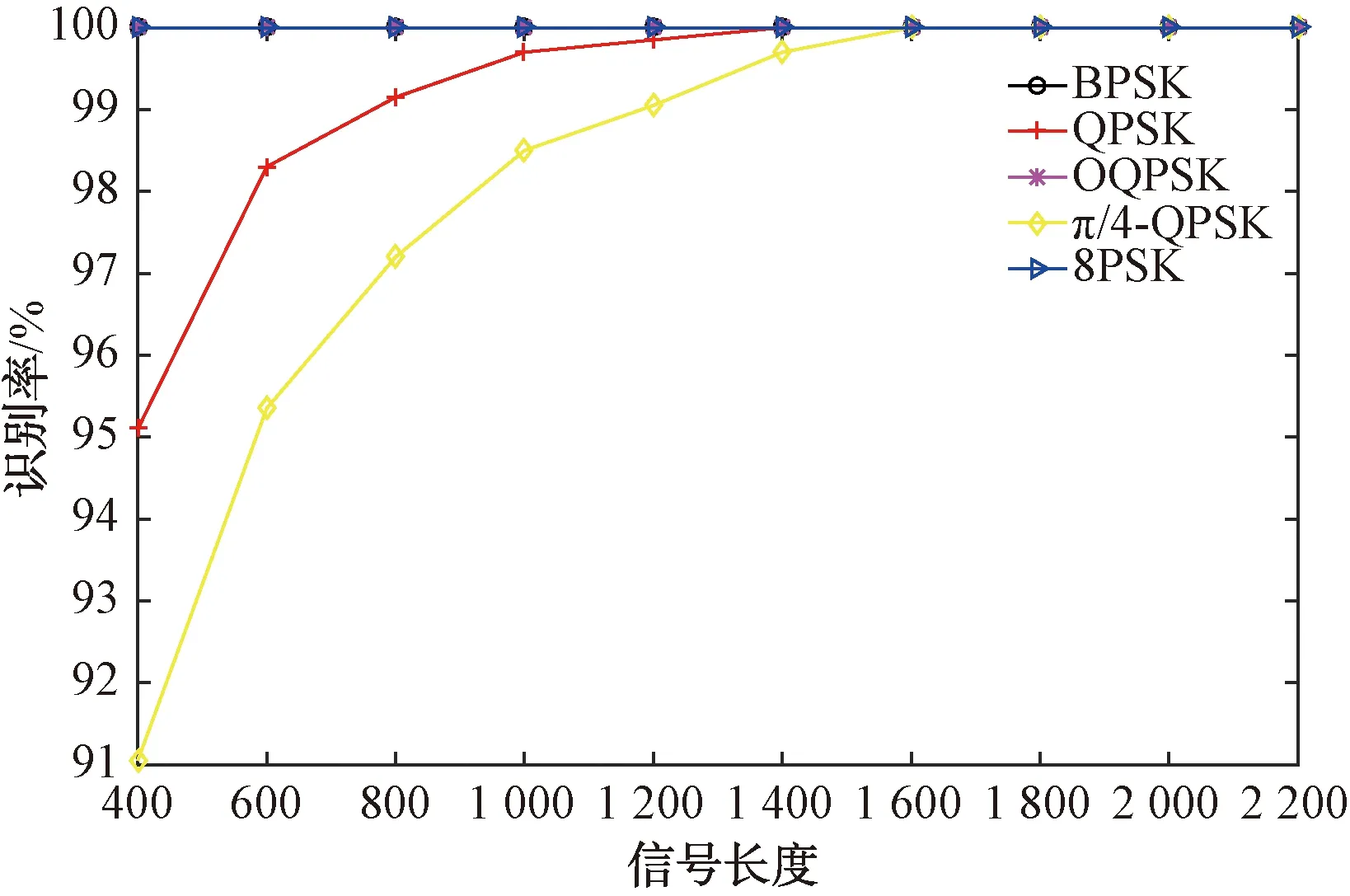
圖9 不同信號長度下信號識別率情況

(2) 不同信噪比下算法識別性能

設定載波剩余相位殘差為0,信號長度N=1 600,判決門限h1=0.085,h2=0.05,信噪比5～20,信噪比步徑間隔為1,每種信號2 000次識別,不同信噪比下信號的識別性能如圖10所示。根據圖10可知,隨著信噪比增加,信號的識別率逐漸增大,當信噪比等于10 dB時,幾種調制信號的識別率可達到100%。

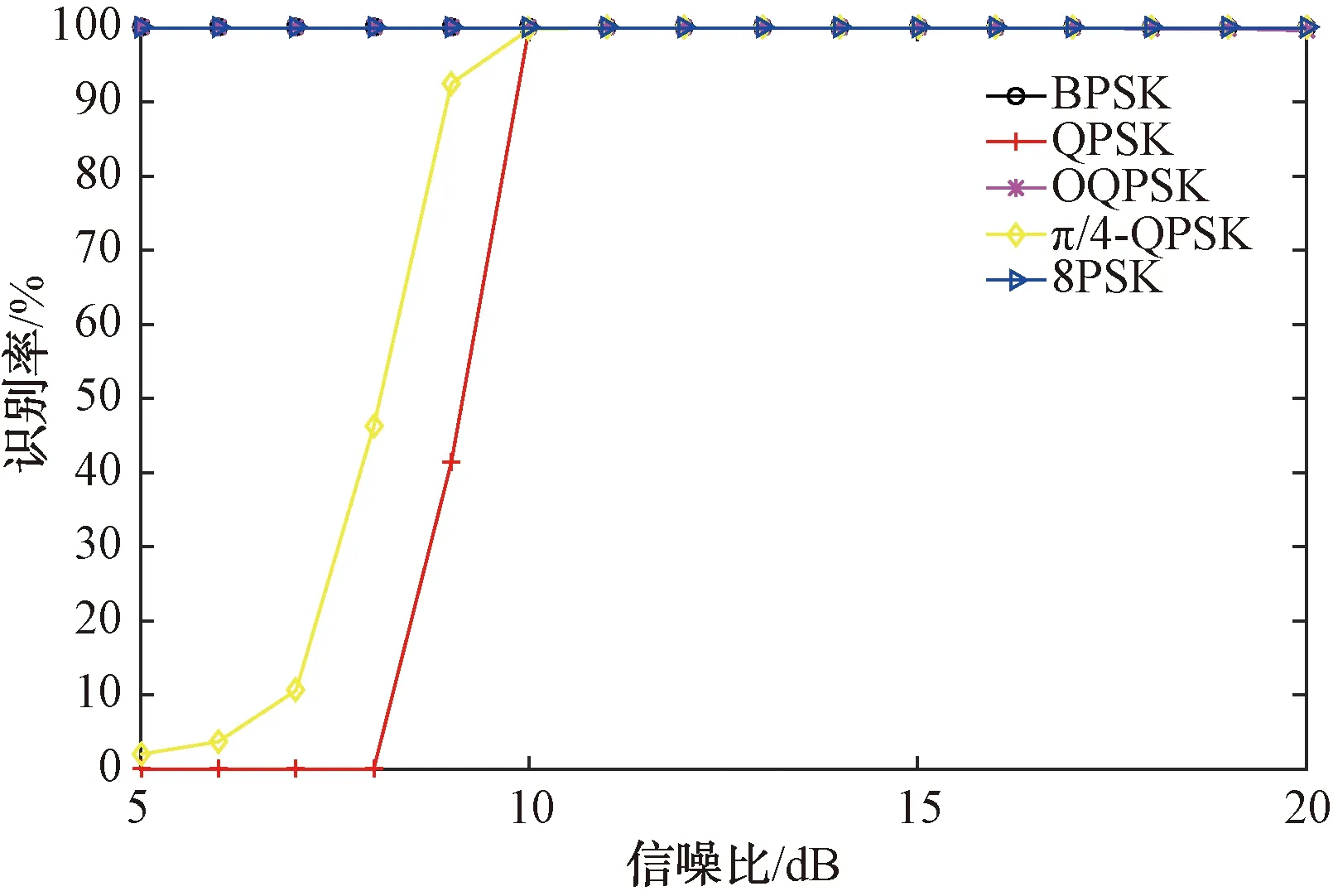
圖10 不同信噪比下信號識別率情況

(3) 不同載波剩余相位下算法識別性能

設定載波剩余相位取{0、5°、15°、25°},信號長度N=1 600,判決門限h1=0.085,h2=0.05,信噪比5～20,信噪比步徑間隔為1,每種信號2 000次識別,不同信噪比下信號的識別性能如圖11所示。根據圖11可知,該算法對于載波殘余相位不敏感。

圖11 不同載波殘余相位下信號識別率情況

4 結束語

對于MPSK類內{BPSK、QPSK、OQPSK、π/4-QPSK、8PSK}這幾種調制樣式信號,本文提出了一種基于高階累積量和差分星座最小環帶模值方差進行信號調制樣式識別的算法。首先利用四階累積量將信號區分為BPSK、{QPSK、OQPSK}、{π/4-QPSK、8PSK}三大類,然后利用差分星座最小環帶模值方差進一步將QPSK、OQPSK、π/4-QPSK、8PSK子類信號區分出來。通過仿真表明,當信噪比增加到10 dB,信號長度為1 600的情況,這5種信號的識別率可以達到100%。同時,仿真表明該識別算法對載波殘余相位不敏感,算法的魯棒性較好。