一種改進抽樣函數自適應濾波的抗靈巧噪聲干擾方法

閔柏成,張世超,陳凱翔,邱碩豐

(中國船舶集團有限公司第八研究院,江蘇 揚州 225101)

0 引 言

近年來,隨著脈沖壓縮技術的發展,現代機載雷達的抗干擾能力大大提高,傳統噪聲干擾對脈沖壓縮雷達的干擾能力大幅下降。針對此問題,國內外學者對靈巧噪聲干擾[1]這種新型干擾頗為重視。針對脈沖壓縮雷達信號處理的特點,靈巧噪聲干擾由干擾機截獲的雷達發射信號和本地噪聲調制而成,這樣在提高了傳統噪聲干擾相參性的同時,也將噪聲能量集中起來,從而對脈沖壓縮雷達造成了壓制性和欺騙性雙重干擾效果。

線性調頻(LFM)脈沖壓縮體制的機載雷達在靈巧噪聲干擾環境中,干擾對目標回波形成極好的壓制性和欺騙性干擾效果[2],導致常規的抗干擾措施無法在時域及頻域分離干擾和目標回波。針對此問題,目前已有多種靈巧噪聲干擾的抑制方法。文獻[3]通過對噪聲和脈沖卷積2種靈巧干擾方式的干擾效果進行分析,給出了一種特殊的波形設計。該波形結合了參數捷變和低截獲二者的理念,達到了一定的抗干擾效果。文獻[4]從宏觀角度介紹了靈巧干擾的概念、發展過程、分類,通過干擾的作用機理和干擾效果,概括并分析了靈巧噪聲干擾的抑制方法。文獻[5]通過對靈巧噪聲干擾的假目標數量與卷積噪聲干擾的信號時寬進行分析,其仿真結果表明二者成正比關系。文獻[6]通過自適應旁瓣對消系統可有效抑制靈巧噪聲干擾。以上文獻均對線性調頻脈沖壓縮體制的機載雷達抗靈巧噪聲干擾提供了參考,但其研究重點基本保持在靈巧干擾本身的干擾效果及干擾調制方式上,針對線性調頻信號雷達本身的抗干擾效果并不明顯,且這些方法都有一定的局限性,不具有普適性。

針對靈巧噪聲干擾對脈沖壓縮雷達造成的壓制性和欺騙性雙重干擾效果的問題,本文首先通過差拍處理,使信號和干擾在頻域實現解耦分離,然后采用改進抽樣函數的變步長濾波算法,濾除解耦后的回波信號分量,最后對消解耦前后的干擾分量,通過逆差拍處理方式恢復目標回波信號。利用本文所提的方法可有效地抑制靈巧噪聲干擾,無需對干擾進行參數估計,并能較好地恢復目標回波。

1 信號和干擾模型

LFM脈沖壓縮體制的機載雷達具有較高的速度測量精度和速度分辨力,其發射信號通常具有較長的時寬與較大的帶寬。同時,靈巧噪聲干擾作為一種新型干擾方式,與LFM雷達的目標回波具有很多相似之處,因此對目標回波信號具有很強的欺騙性。此外,在這種新型干擾方式下,目標回波信號的帶內集中了能量較強的干擾信號,從而壓制目標回波[7]。

設第m個脈沖重復周期雷達發射信號為:

(1)

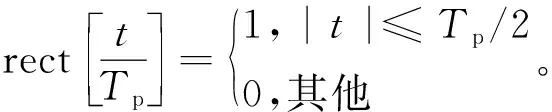
此時,雷達的回波信號為:

sR(t,m)=a(m)sm′(t-τ(m))

(2)

(3)

式中:a(m)表示目標回波的幅度;τ(m)表示目標回波的時延;fd(m)為目標回波的多普勒頻移。

目前,應用較廣泛的靈巧噪聲干擾是通過干擾機截獲的雷達發射信號與本地噪聲卷積調制而成[7],為達到更好的欺騙干擾效果,對卷積噪聲干擾進行移頻處理,通過改變移頻量形成具有壓制效果的假目標干擾,使真實的目標回波在時域及頻域完全被淹沒在干擾中。

根據式(1)及靈巧噪聲的產生方法,第m個脈沖重復周期經移頻后的卷積噪聲干擾如下:

(4)

式中:b(m)表示第m個脈沖重復周期靈巧噪聲干擾的幅度;τj(m)表示第m個脈沖重復周期靈巧噪聲干擾的時延;fyp為移頻量;n(t)為視頻噪聲信號。

2 靈巧噪聲干擾抑制算法

根據目標回波和靈巧噪聲干擾的時域匹配接收、頻譜特性等,提取干擾特征[8],識別出靈巧噪聲干擾后,通過抗干擾算法對靈巧噪聲干擾進行處理。

2.1 差拍處理

假設干擾機截獲第m個脈沖重復周期中的雷達信號,干擾機對該信號進行移頻處理后進行卷積調制,并在該重復周期內與雷達目標回波一起進入雷達接收機,此時雷達接收信號如下:

Xm(t)=sR(t,m)+Jm(t)

(5)

由于雷達發射信號在第(m-1)個周期中未被截獲,因此在該周期內雷達接收機中僅包含雷達目標回波。此時,利用第m和(m-1)個脈沖重復周期中的接收信號進行差拍處理[9],具體計算過程如下:

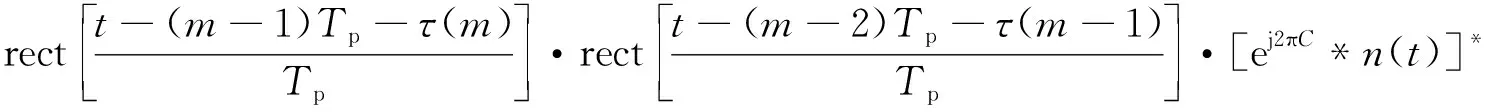
(6)

A={[fd(m-1)-fd(m)]+k[τ(m-1)-τ(m)]}t+[τ(m-1)-τ(m)]f0+

(7)

B=f0(t-τ(m-1))+k(t-τ(m-1))2/2

(8)

C=f0(t-τj(m))+k(t-τj(m))2/2+fypt

(9)

根據式(7)中A可知,雷達目標回波經差拍處理后變成單載頻信號,其信號頻率為:

ft=[fd(m-1)-fd(m)]+

k[τ(m-1)-τ(m)]

(10)

式中:第1項可通過目標加速度、脈沖重復頻率及光速表示:

fd(l)-fd(l+1)=-2a/(cfp)

(11)

通常情況下,目標加速度遠小于光速與脈沖重復頻率的乘積,使fd(l)-fd(l+1)≈0。相對于同一目標而言,LFM機載雷達相鄰脈沖重復周期的時延差很小,使τ(m-1)-τ(m)≈0。因此,ft≈0。

根據式(8)、(9)中B和C可知,靈巧噪聲干擾經差拍處理后未消去與時間t相關的二次項,其干擾信號形式仍為經一定移頻處理的噪聲卷積干擾。此時分為以下2種情況:

(1) 當移頻量fyp=0時,靈巧噪聲干擾的中心頻率由第m-1個脈沖重復周期的目標時延τ(m-1)和第m個脈沖重復周期的干擾時延τj(m)共同決定,如果|k[τj(m)-τ(m-1)]|的值大于干擾帶寬的一半,此時差拍處理后的目標回波與靈巧噪聲干擾可在頻域上基本實現完全分離。此時,任意選取低通濾波器即可實現目標與干擾的分離,通過對消實現靈巧噪聲干擾的抑制。

(2) 當移頻量fyp≠0或|k[τj(m)-τ(m-1)]|的值小于干擾帶寬的一半時,前者通過改變移頻量使靈巧噪聲干擾對目標回波產生壓制效果,后者是由于目標回波落入了靈巧噪聲干擾的信號帶寬內,此時,傳統的濾波方法無法有效實現對回波信號的濾波,干擾對消效果下降。因此,本文采用改進抽樣函數自適應濾波方法實現干擾對消。

2.2 改進抽樣函數自適應濾波器原理

信號經差分處理后,目標回波信號ft位于接近于零的低頻處,結合自適應陷波器的基本原理,對差分處理后的回波信號進行陷波處理,進而通過干擾對消的方式抑制靈巧噪聲干擾,最終通過逆差拍處理恢復目標回波。

傳統的自適應陷波原理框圖如圖1所示。

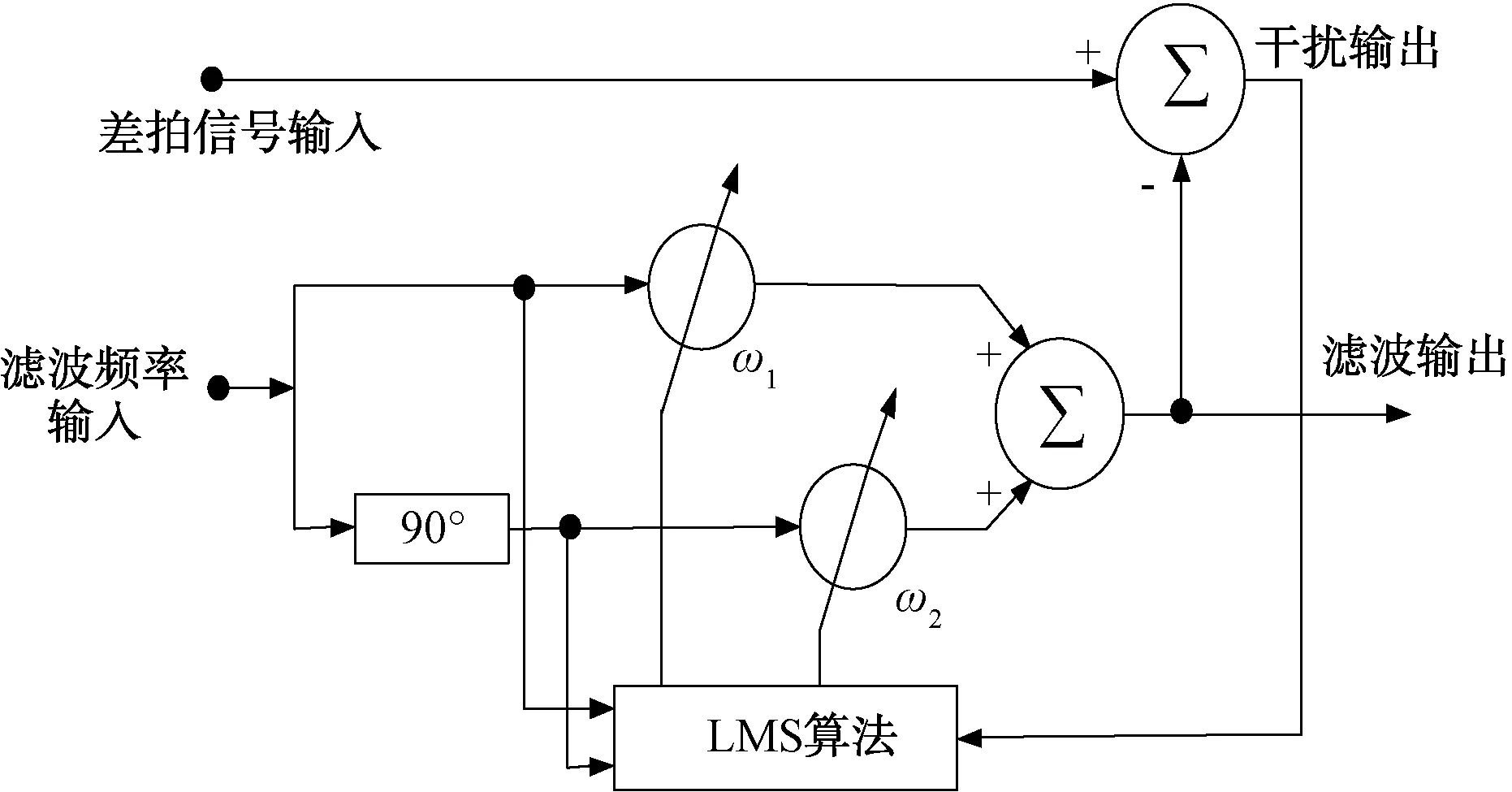
圖1 傳統自適應陷波原理框圖

由圖1可知,差拍信號輸入為經差拍處理后目標回波分量及干擾分量的混合信號,濾波輸入頻率為f0的正弦信號。

由差拍信號輸入到干擾輸出的自適應沖激相應函數為:

(12)

式中:f0為需要進行濾波的頻率值;μ為自適應濾波器的步長;a為濾波頻率輸入的信號幅值。

由于差拍處理后目標回波信號ft≈0,則令濾波頻率輸入f0=0,代入式(12)得:

(13)

通過式(13)可以看出,陷波器在單位圓內存在零點和極值點各一個,分別落在z=1和2μa2處。此時,在(0,ln(2μa2)/2π)區間范圍內,可濾除ln(2μa2)/2π帶寬內的頻譜,該帶寬的大小由自適應步長μ決定。

為實現靈巧噪聲干擾的有效抑制,本文采用的改進抽樣函數自適應LMS算法[10]如下:

e(n)=d(n)-cT(n)ω(n)

(14)

(15)

ω(n+1)=ω(n)+2μ(n)e(n)c(n)

(16)

式中:e(n)為n次迭代后的陷波輸出信號;d(n)為n次迭代后的干擾對消信號;c(n)為第n次迭代時的濾波函數輸入;ω(n)為第n次迭代時的加權;α為幅值調整系數;β為波形控制系數。

根據式(15)可知,改進抽樣函數將抽樣函數中心值進行翻轉,并通過α、β的取值保證函數曲線[11]。由圖2可以看出,改進抽樣函數曲線中的步長與誤差之間的對應關系,通過幅值調整系數α可控制陷波帶寬,通過波形控制系數β控制函數的收斂速度。

圖2 抽樣函數改進前后曲線對比

由于自適應陷波算法中,步長μ的大小決定了陷波帶寬,通過合理的步長曲線可使陷波效果達到最優,針對2.1節中經差拍處理后目標回波分量及靈巧噪聲干擾分量的耦合情況來選取α、β的取值可使陷波效果更優,并能有效對消干擾分量。

幅值調整系數α和波形控制系數β對步長曲線的影響如圖3所示。由圖3可以看出,通過控制β值改變步長的變化率,步長變化率即β的取值越小,步長變化越慢,此時陷波器的陷波效果主要取決于α的取值。當幅值調整系數α取值較大時,由于β取值相對較小,陷波器的陷波帶寬較大,且在算法整個迭代過程中,更多情況處于較大陷波帶寬中,此情況適用于靈巧噪聲干擾的移頻調制量fyp=0,且|k[τj(m)-τ(m-1)]|大于干擾帶寬的一半。通過大且變化較慢的陷波帶寬可更有效地濾除回波信號,干擾對消效果更加明顯。

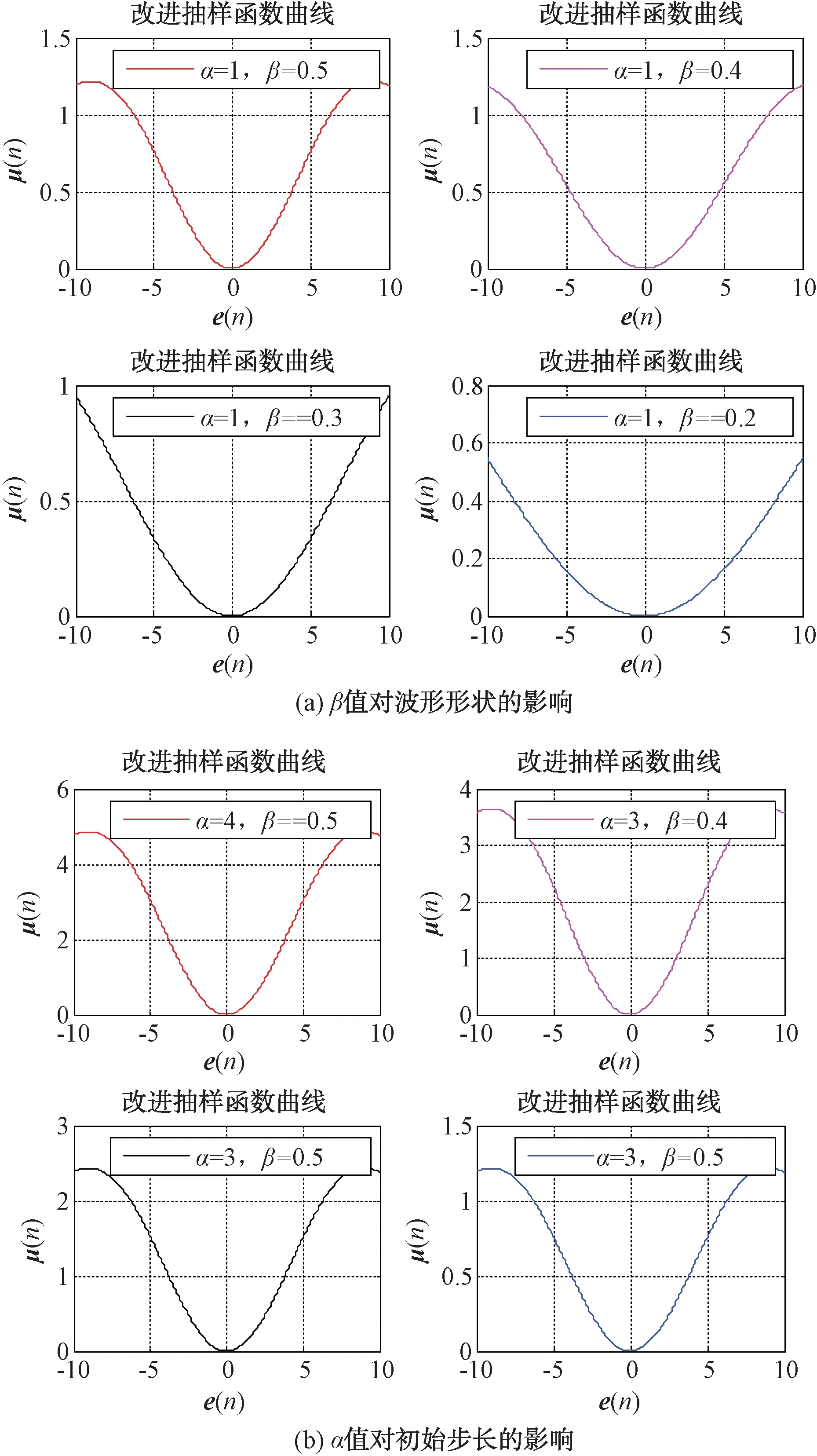
圖3 2個系數對步長曲線的影響

當移頻量fyp≠0或|k[τj(m)-τ(m-1)]|的值小于干擾帶寬的一半時,干擾信號與目標回波經差拍處理后仍存在部分耦合。此時,通過較小的初始步長和較大的步長變化率(即α取值較小,β取值較大)可更有效地濾除目標回波并對消靈巧噪聲干擾。

2.3 抗靈巧噪聲干擾的算法流程

本文所提的抗靈巧噪聲干擾的算法流程如圖4所示,可分為4個步驟:

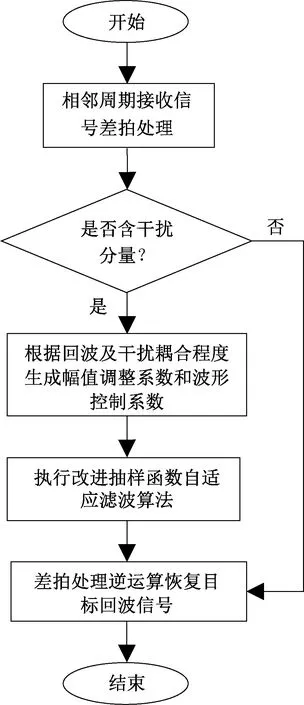
圖4 抗靈巧噪聲干擾的算法流程圖

步驟1,根據式(6)對雷達接收機中相鄰2個周期的接收信號做差拍處理,使真實目標回波信號消除二次項。

步驟2,根據差拍處理后的信號頻譜,判斷真實目標回波信號與靈巧噪聲干擾信號的耦合程度,生成改進抽樣函數的幅值調整系數α和波形控制系數β。

步驟3,通過式(14)～(16)完成差拍處理后靈巧噪聲干擾分量的對消。

步驟4,通過差拍處理的逆運算恢復目標回波信號。

3 仿真驗證及分析

3.1 算法流程仿真

仿真參數設置為:LFM雷達信號的中心頻率f0=50 MHz,帶寬B=100 MHz,脈沖寬度τPW=50 μs,脈沖重復周期為500 μs,線性調頻信號的斜率k=BτPW。根據2.1節的分析,移頻量、回波時延和干擾時延的設置分以下2種情況:

情況1:當移頻量fyp=0且|k[τj(m)-τ(m-1)]|的值大于干擾帶寬Bj一半的情況時,取τi(1)=80 μs,τj(2)=110 μs。

情況2:當移頻量fyp≠0或|k[τj(m)-τ(m-1)]|的值小于干擾帶寬Bj一半的情況時,取τi(1)=80 μs,τj(2)=90 μs,fyp=2 MHz。

圖5(a)和圖5(b)分別為無干擾條件下LFM信號的時域波形和幅頻圖;圖5(c)和圖5(d)分別為基于情況1和情況2參數設置的情況下,LFM回波信號受靈巧噪聲干擾的幅頻圖。可以看出,2種情況下LFM目標回波信號的頻譜成分完全被靈巧噪聲干擾所淹沒,無法通過當前頻譜信息提取有用信息。圖5(e)和圖5(f)分別表示在有無干擾情況下信號的匹配濾波輸出結果。可以看出,存在干擾的目標回波經匹配輸出后,干擾和目標同時獲得處理增益,LFM目標回波信號經脈壓處理后被靈巧噪聲干擾壓制。因此,LFM回波信號與靈巧噪聲干擾在時域及頻域上完全耦合。

圖5 LFM回波在有無靈巧噪聲目標干擾下的對比仿真圖

根據本文所提的算法,首先對2種干擾情況下的混合信號進行差拍處理。圖6(a)為回波時延τi(1)=80 μs,干擾時延τj(2)=110 μs時混合信號經差拍處理后的幅頻圖。圖6(b)為回波時延τi(1)=80 μs,干擾時延τj(2)=110 μs,fyp=2 MHz時混合信號經差拍處理后的幅頻圖。可以看出,經差拍處理后,LFM的目標回波分量與靈巧噪聲干擾分量實現了在頻域上的分離。相比于第2種情況,差拍處理在情況1干擾條件下目標回波與干擾的分離效果更好。然后根據2種情況干擾與回波信號的分離效果,在情況1干擾的條件下,設置濾波器中的幅值調整系數α=4和波形控制系數β=0.5,經濾波及干擾對消后信號的幅頻圖如6(c)所示。在情況2干擾的條件下,設置濾波器中的幅值調整系數α=1和波形控制系數β=0.2,經濾波及干擾對消后信號的幅頻圖如6(e)所示。最后對濾波對消后的信號進行逆差拍處理,2種情況下目標回波的恢復情況如圖6(d)和6(f)所示。通過圖6(c)～6(f)可知,經本文所提的改進抽樣函數自適應濾波器后,可有效對消2種情況的干擾分量。與圖5(b)中LFM幅頻圖相比,可根據幅值調整系數和波形控制系數實現有效濾波,并能良好地恢復LFM目標回波信號。

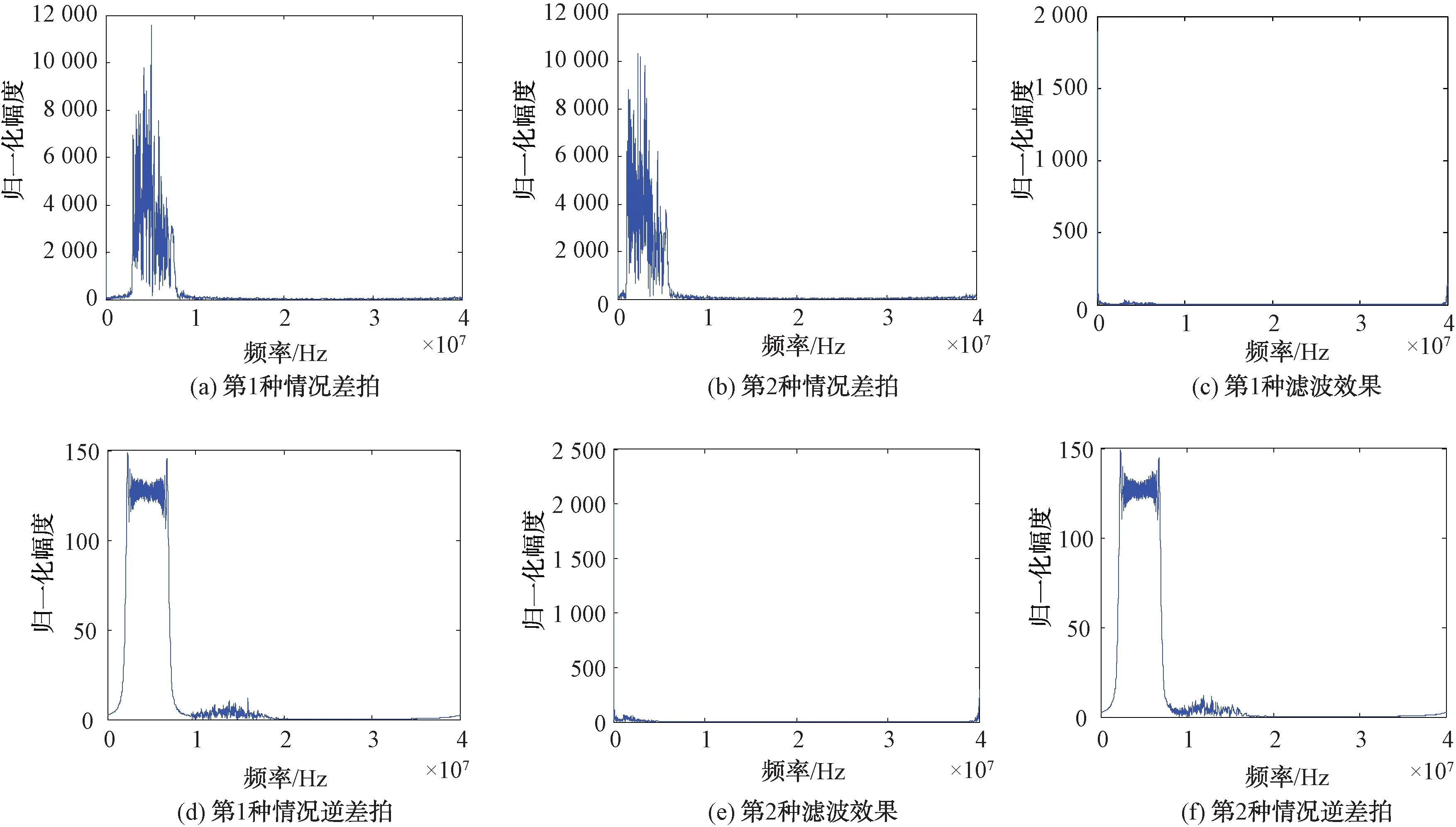
圖6 抗靈巧噪聲干擾前后對比仿真圖

3.2 干擾抑制結果及分析

針對第1種情況下的干擾,通過改變幅值調整系數α的值來分析本文所提方法的干擾抑制性能。其參數設置如下:算法處理前目標回波與靈巧噪聲干擾的初始信干比為δSJR=-10 dB,β=0.5,α=1,2,3,4,算法迭代次數N=2 000,其它參數設置情況與3.1節保持一致。經100次Monte Carlo實驗[12],得到算法處理前后的信干比變化隨迭代次數的變化情況如圖7所示。由圖7可以看出,隨著幅值調整系數α的增大,其算法處理后干擾抑制效果更加明顯。相比于普通抽樣函數的幅值調整系數α=1時,濾波后的信干比提高了25 dB左右。因此,采用本文所提的改進抽樣函數自適應濾波方法,在移頻量fyp=0且|k[τj(m)-τ(m-1)]|的值大于干擾帶寬Bj的一半時,可有效抑制靈巧噪聲干擾。相比于定步長自適應濾波算法,干擾抑制后信干比至少提高10 dB,通過改變幅值調整系數α,可使信干比提高30 dB以上。

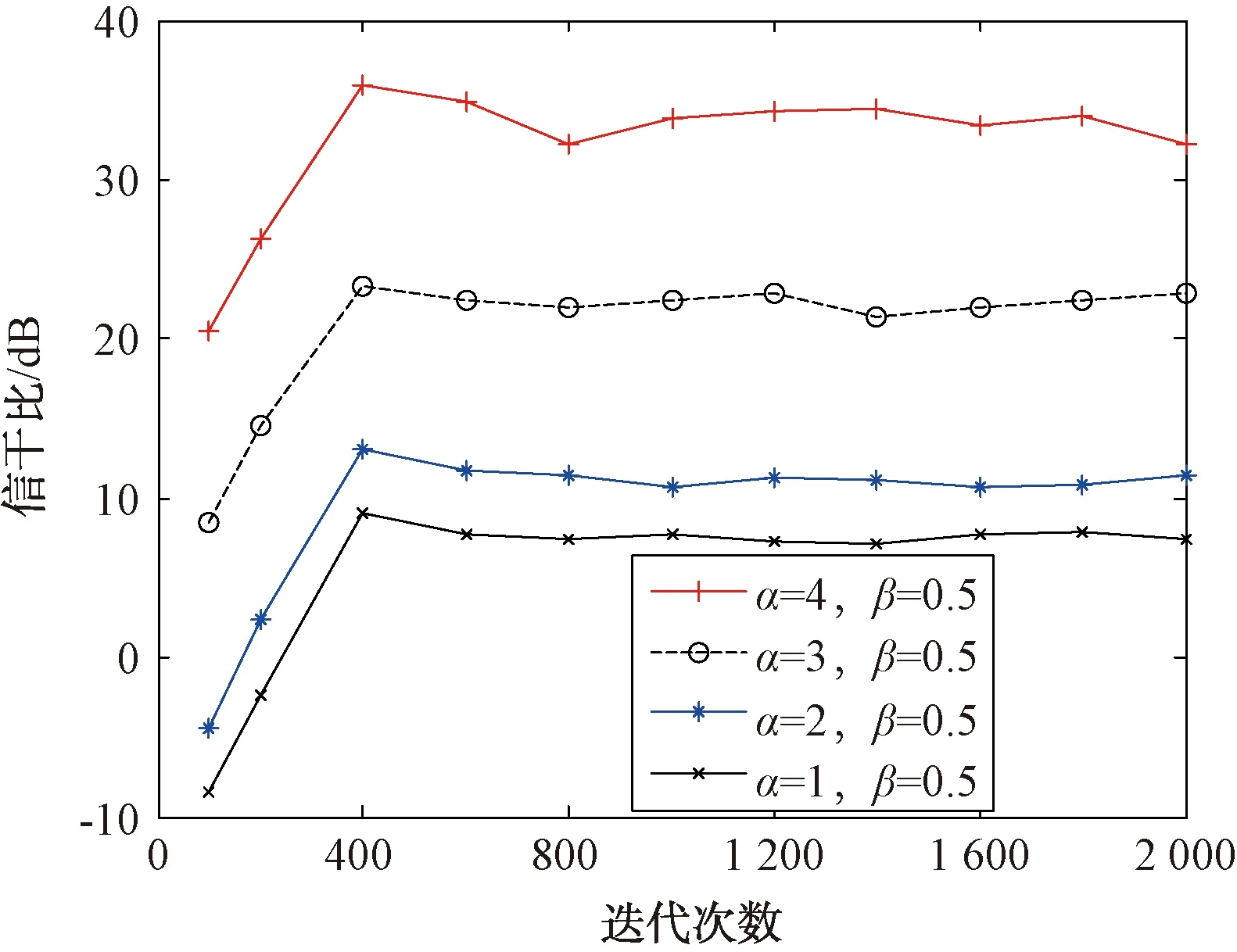
圖7 不同α值對情況1的干擾抑制效果仿真圖

針對第2種情況下的干擾,通過改變波形控制系數β的值來分析本文所提方法的干擾抑制性能。其參數設置如下:算法處理前,目標回波與靈巧噪聲干擾的初始信干比為δSJR=-10 dB,β=0.2,0.3,0.4,0.5,α=1,算法迭代次數N=2 000,其它參數設置情況與3.1節保持一致。經100次Monte Carlo實驗,得到算法處理前后的信干比變化隨迭代次數的變化情況,如圖8所示。由圖8可以看出,隨著波形控制系數β的增大,其算法處理后干擾抑制效果更加明顯。相比于普通抽樣函數的波形控制系數β=1時,濾波后的信干比提高了15 dB左右。因此,采用本文所提的改進抽樣函數自適應濾波方法,在移頻量fyp≠0或|k[τj(m)-τ(m-1)]|的值小于干擾帶寬Bj的一半時,可有效抑制靈巧噪聲干擾,相比于定步長自適應濾波算法,干擾抑制后信干比至少提高8 dB。通過改變波形控制系數β,可使信干比提高20 dB以上。

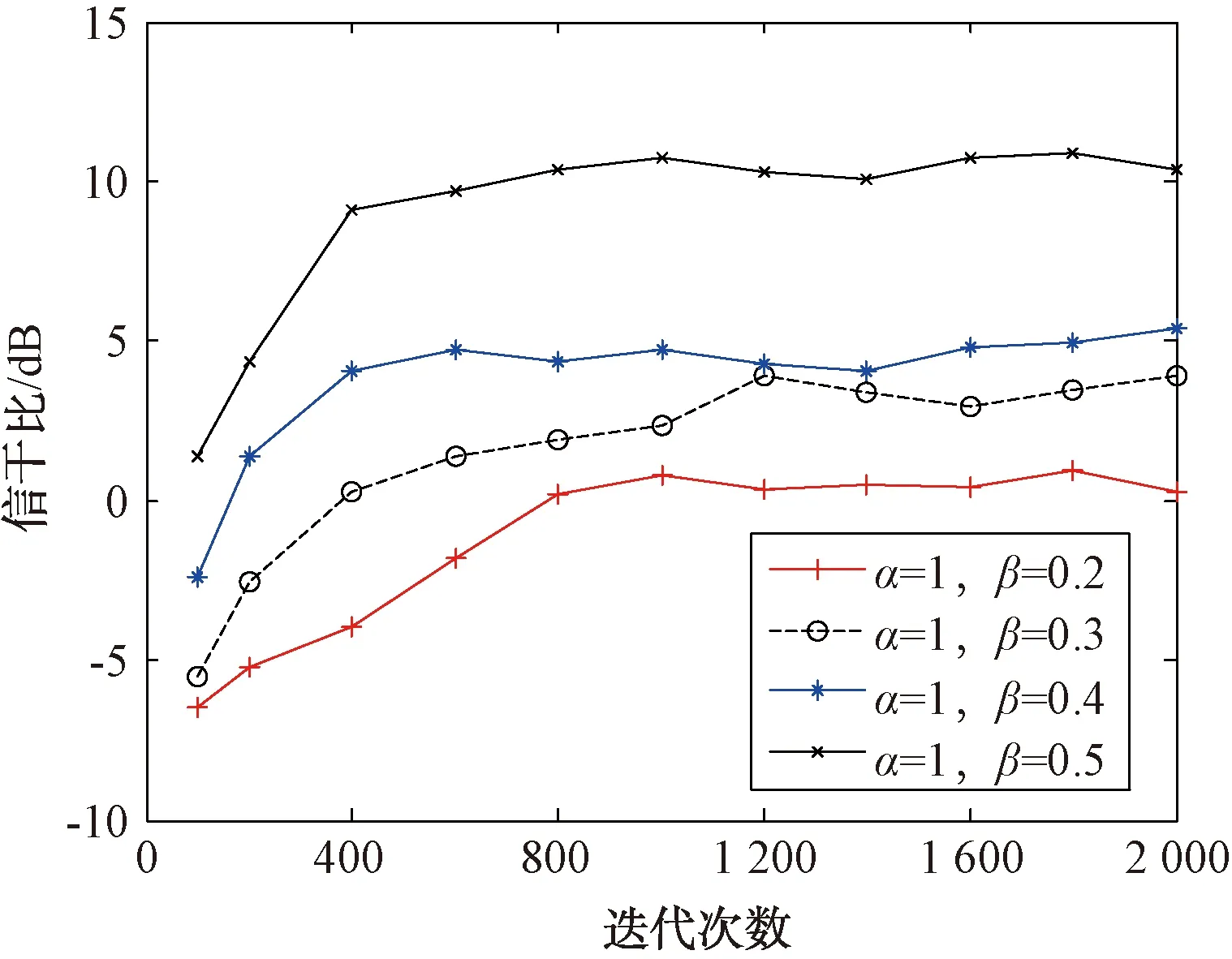
圖8 不同β值對情況2的干擾抑制效果仿真圖

4 結束語

靈巧噪聲干擾對LFM體制的機載雷達產生較強壓制性和欺騙性,使目標回波信號在頻域上完全被淹沒,匹配濾波后干擾對回波造成完全的欺騙效果。針對此問題,本文采用了一種改進抽樣函數的自適應濾波方法,通過幅值調整系數和波形控制系數,對差拍處理后的回波信號分量進行濾波處理,并對消靈巧噪聲干擾。通過本文的仿真結果可以看出,改進抽樣函數濾波算法可有效提取在2種干擾情況下的目標回波,消除靈巧噪聲干擾的影響。