APOS理論對中學數學教學的啟示
朱怡祺 喻平


摘 要:APOS理論的一個基本假設是,數學知識的心理建構需要經歷操作、過程、對象和圖式四個階段。這四個階段不是一種線性關系,而是一個循環系統。APOS理論主要是針對概念學習的。從教學的角度看,四個階段之間的轉化機制比四個階段本身更有意義。由此,在中學數學教學中,教師應當采取適當的策略促進學生四種心理狀態之間的轉化,具體包括:用活動促進內化,用概括實現壓縮;用新知促進解壓,用系統生成圖式。
關鍵詞:中學數學;APOS理論;概念教學;轉化機制;圖式
*
本文系喻平教授團隊的“數學學習心理學研究及其教學啟示”(中學)系列文章之十六。
APOS理論是美國學者杜賓斯基等基于皮亞杰的“反思抽象”觀點提出的一種建構主義的數學學習理論。他們認為,人們透過心智結構使學習的數學概念產生意義,而教學的目的就在于幫助學生建立適當的心智結構。再讀APOS理論,可以看到它對中學數學教學很有指導價值。
一、 APOS理論概述
APOS理論主要涉及四個概念:操作(Action)、過程(Process)、對象(Object)和圖式(Schema)。[1]具體地說,操作、過程、對象和圖式是數學學習中的一種心理結構。對某一數學對象實施操作,這種操作經過內化成為過程,過程可以被壓縮為一個完整的對象,整個系統成為圖式。[2]
(一) APOS理論的基本假設
APOS理論的一個基本假設是:數學知識是個體在解決所感知的數學問題的過程中獲得的,在這個過程中個體要進行心理建構,這種建構需要經歷四個階段。在學習過程中,學生對教師提供的外部信息進行辨認,將其轉換為一系列操作,通過親身體驗,感受直觀背景和數學概念之間的關系,這是操作階段。學生經過多次操作和反思后,便能通過想象執行一系列指令,抽象出概念的本質特征,在大腦中進行一種內部的心理建構,即形成一種過程模式。[3]這種模式使得操作呈現出自動化的表現形式,而不再借助于外部的不斷刺激,學生從依靠外在的提示轉向依靠內部的調控,這是過程階段。而學生意識到轉換可以運用于整體,并且實際可以建構這樣的轉換時,就達到了對象階段。在這一階段,給抽象出的本質特征賦予形式化的定義和符號,也就是說,學生把過程看作一個整體,并對它進行轉換和操作時,過程也就凝聚成了對象。
包括操作、過程、對象在內的整個認知系統即為圖式。杜賓斯基指出,任何圖式的開發都涉及三個階段:圖式內部、圖式之間、圖式遷移。圖式內部階段的特點是,個體只注意離散的操作、程序和對象,而把具有類似性質的其他知識點隔離開來;在圖式之間階段,個體注意到各個圖式中蘊涵的知識點之間的關系和銜接,從而能把這些知識點組成一個整體;在圖式遷移階段,個體徹底清楚知識點之間的關系,建構出這些點之間的內部結構,形成一個大的圖式,最終能判斷哪些問題存在于這個圖式,哪些問題超出了這個圖式的范圍。[4]
(二) 對APOS理論的幾點認識
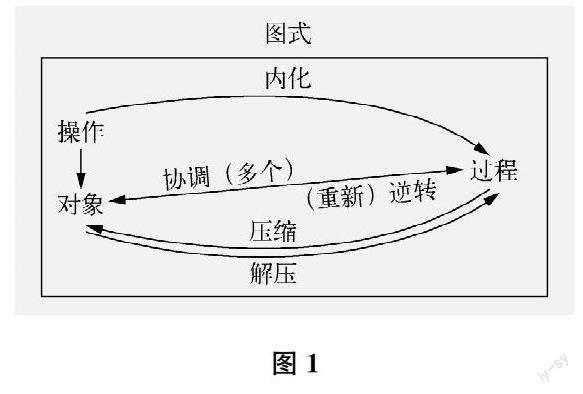
其一,四個階段不是一種線性關系,而是一個循環系統。如圖1,操作階段通過將外部信息轉化為內部信息,逐漸脫離相對具體的情境,轉變上升為心理上的操作,不再完全依賴具體的被操作對象和實際問題。經過多次操作之后,進入過程階段,這就是內化。這時,學習者得到了一堆關于知識的信息,就需要去除一些枝節,梳理出最精華的成分,從而進入對象階段。從過程階段到對象階段,需要將內化的心理操作簡約和抽象(形成直覺),這就是壓縮。[5]只有當個體嘗試對過程進行壓縮時,才有可能將動態的結構轉化為可以應用的靜態結構;只有當個體意識到過程可以作為整體時,才能形成對象。當然,也存在這樣一種情況,即簡單的操作或達到高度自動化的操作可以直接形成對象。過程被壓縮成心理對象之后,還可以在需要引發時解壓為潛在的過程。經過解壓機制,個體能將對象還原為先前的過程。兩個對象在分別解壓為先前的過程后,可能相互協調并重新被壓縮為一個新的對象。逆轉則是建構新對象的另一個心理機制。某一過程在逆轉機制的作用下形成的新過程,將被重新壓縮為新的對象。[6]
其二,APOS不是一種教學模式,而是學習數學的一種心理結構。教學模式包含的基本要素是理論基礎、教學目標、教學程序、教學策略以及教學評價。顯然,APOS框架不具有這些屬性,因而不屬于教學模式。當然,從操作、過程、對象、圖式四個階段來看,確實體現了一種知識學習的“程序”,或者說學習者對信息的加工過程。可以根據這個心理過程設計相應的教學步驟,但是,這個心理結構的描述本身不能稱為教學模式。
其三,并非所有數學知識的學習都能用這個結構來解釋。杜賓斯基提出這個理論,主要針對的是概念學習,諸如大量的命題學習、思想方法的學習等,難以用這種心理結構來描述。事實上,許多數學概念本身就具有“過程”與“對象”的雙重性。斯法德提出,數學中的許多概念(特別是代數概念)在具有過程性的同時,又表現出對象性;過程性指具備可操作的法則,對象性指概念的結構。[7]例如,加法既代表兩個集合中的元素合并或添加起來的過程,又代表合并或添加起來的結果;軸對稱既代表圖形關于指定直線翻折的過程,又代表圖形之間具有的特定性質或位置關系;數列極限既代表數列變化趨勢的過程,又代表變化趨勢的結果。因此,概念的雙重性決定了學習心理也會表現出這兩個特性。
其四,經歷四個階段,就是對知識的建構過程。所謂建構性學習,是指學習者通過對一類事物的認識,結合已有的知識、經驗,概括出一類事物本質屬性來形成知識,并與同伴交流、協商使知識精確化的過程。學生經歷的操作、過程、對象、圖式四個階段恰好是知識建構的各個環節(當然,主要是個人建構,缺少社會建構),整個學習過程體現出建構主義思想和知識建構的基本理路。
二、 對中學數學教學的啟示
從教學的角度看,四個階段之間的轉化機制比四個階段本身更有意義。在圖1中可以看到,內化、壓縮、解壓、協調、逆轉等就是要素之間轉化的心理機制。APOS理論的價值不在于依據四個階段設計教學,而在于如何干預內化、壓縮、解壓等心理機制,使從操作到過程到對象再到圖式的轉化得以實現。因此,研究如何實現心理狀態之間的轉化,才有真正意義上的教學論價值。
(一) 用活動促進內化,用概括實現壓縮
在APOS循環中,要實現從操作到過程的過渡需要內化。而內化的實現,需要個體主動地反復操作實施相應的活動。因此在中學數學教學中,教師應當合理設計操作環節,讓學生通過活動促進內化。這里的“活動”一是指動手操作的外顯活動,二是指頭腦中的思維活動,因此與通常所說的“做數學”含義相同。“做數學”是學生在教師的指導下,利用一定的工具(實物或軟件),通過動手操作、觀察思考、歸納抽象等過程建構數學概念、驗證數學結論、探索數學規律、解決數學問題的一種學習方式。可以看到,“做數學”的過程能夠充分激發學生的思維,促進行為的內化。
另一方面,從過程到對象的心理機制是壓縮。壓縮的隱喻是擠出事物的水分,使其瘦身,本質是拋棄無關信息,找出一類事物的共同特征和本質屬性。因此,教師要引導思維方向,清除思維障礙,讓學生通過概括來實現壓縮。概括是指人腦在比較和抽象的基礎上,把抽象出來的事物的共同本質特征綜合起來,并推廣到同類事物上去的過程。
這里,教師預計學生在函數概念的理解中可能出現的問題,由此設計一系列涉及多個知識點、綜合性較強的變式練習,從而促使學生通過解壓回到過程階段,還原先前的探究操作,再進一步協調,重新壓縮得到新的對象。
杜賓斯基指出,個體對概念理解的深度和復雜性,取決于他在構成這個概念的心理結構之間建立聯系的能力。這些聯系構成了圖式的基礎,而圖式的連貫性對個體理解與概念相關的數學情境的能力至關重要。圖式是對事物的綜合性表征,它是命題網絡、表象表征和線性排序的組合。[9]加涅概括了圖式的三個特征:(1) 圖式含有變量;(2) 圖式可以按層級組織起來,也可以嵌入另一個圖式之中;(3) 圖式能促進推論。[10]圖式含有變量是指,圖式中的許多屬性是允許改變的。例如,函數的本質是數集到數集的映射,但它的表現形式是多樣的:解析式表征、圖像表征、表格表征等。函數圖式按層級組成指的是,一些特殊的函數作為一般函數的子圖式,而函數本身又是映射的子圖式。圖式的第三個特征主要指,一級圖式的許多性質可由上一級圖式直接推出。例如,指數函數必然有定義域、值域和對應關系,這些信息沒有必要在定義指數函數y=ax(a>0)時給出,因為作為子圖式,指數函數嵌入函數圖式之中,具有函數的所有特征。
幫助學生形成圖式的基本方法有:
第一,對學過的知識進行梳理,可以用具有層次的概念圖作為輔助工具進行表達,從而厘清知識的來龍去脈(縱向發展);同時,還要找出知識之間的橫向聯系。當然,除了建立章節或單元內部的知識網絡,還應打通章節或單元之間的知識聯系。
參考文獻:
[1] S.Lerman.Encyclopedia of Mathematics Education[M].Dordrecht:Springer Netherlands,2014:89.
[2] 鮑建生,周超.數學學習的心理基礎與過程[M].上海:上海教育出版社,2009:96.
[3] A.Ilana,Jim Cottrill,Ed Dubinsky,et al.APOS Theory:A Framework for Research and Curriculum Development in Mathematics Education[M].New York:SpringerVerlag,2014:526.
[4] 喬連全.APOS:一種建構主義的數學學習理論[J].全球教育展望,2001(3):1618.
[5] 李士锜.PME:數學教育心理[M].上海:華東師范大學出版社,2001:114.
[6] 馬曉丹.APOS理論探索的反思與超越[J].教學與管理,2020(33):7477.
[7][8] A.Sfard.On the dual nature of mathematical conception,Reflections and objects as different sides of the same coin[J].Educational Studies in Mathematics,1991(1):136,136.
[8] A.Sfard.On the dual nature of mathematical conception,Reflections and objects as different sides of the same coin[J].Educational Studies in Mathematics,1991(1):136.
[9] 喻平.數學教育心理學(第三版)[M].南寧:廣西教育出版社,2015:61.
[10] E.Gagne.The Cognitive Psychology of School Learning[M].Boston:Litlle,Brown and Company, 1985:81.

