基于有限元的邊墩超高阻尼支座地震響應研究

鄧少雄

摘要：為了研究超高阻尼橡膠支座對剛構矮塔斜拉橋邊墩的地震響應，以實際在建工程項目甘肅天水國際陸港環城公路渭河五號橋（75+126+75）m 為研究對象，基于有限元軟件 Midas Civil 建立橋梁模型和支座、樁基擬合體系并進行非線性時程分析，對比非減隔震和減隔震橋梁的各向內力和位移。結果表明：以人工擬合地震波為基礎波進行結構體系地震輸入時，超高阻尼橡膠支座相比于非減隔震支座而言，支座所在的邊墩處，其墩底位置各向內力、墩頂各向位移均大幅度減小，減隔震效果明顯；中墩墩底位置處的縱向內力和位移數值減小明顯，由于寬幅結構特點，橫向彎矩、橫向剪力、橫向位移均變化不大，總體減隔震效果呈正向分布；設置有超高阻尼支座的橋塔塔底縱橫向內力、塔頂縱橫向位移數值下降較為顯著，內力和位移的隔震率比較突出。

關鍵詞：減隔震；超高阻尼支座；內力；矮塔斜拉橋；位移；地震響應

中圖分類號：U448.27????????????????????????? 文獻標志碼：A

0引言

剛構矮塔斜拉橋因其高次超靜定體系，有著極其優秀的承載效果，作為當前舒緩我國城市公路交通的寬幅結構，此體系在豎向荷載作用下，跨中正彎矩得以有效縮減，對于主墩的結構尺寸和結構形式而言，其設計的外在表現和受力有更多可能性。超高阻尼支座具有非常明顯的力學性能優化和減隔震效果。

早期的超高阻尼支座是從高阻尼橡膠支座開始的。莊學真等[1]以支座加載實驗對橋梁支座進行了不同參數的研究，得到了支座的滯回曲線。袁涌等[2]得出隨加載頻率變化，其等效剛度亦隨之變化，高阻尼橡膠支座具有一定的速度相關性，加載順序也會影響支座的等效水平剛度和等效阻尼比。沈朝勇等[3]以支座試驗的方法對多種外向影響因素分別進行了討論，如溫度對超高阻尼支座的力學性能影響是呈減小趨勢。陳彥江等[4]通過研究加載頻率對支座力學性能的影響，在加載頻率增大的同時剪切性能隨之增大，這也更加驗證了袁涌等人的結論，即加載速度和支座力學性能的相關性。劉涵[5]等人利用1∶2減縮模型研究了阻尼支座結構的破壞形態、滯回性能、變形能力等。臺玉吉[6]等人通過對比四種不同的減隔震支座抗震性能，得到鋼阻尼支座位移性能最優的結論。

除了超高阻尼支座，國內對矮塔斜拉橋的減隔震研究也取得了優異的成果。萬樂樂[7]等人通過有限元與工程實際相結合，分析了摩擦擺支座對矮塔斜拉橋結構的減隔震性能。王偉軍[8]等人研究了近斷層地震動對矮塔斜拉橋地震響應參數敏感性的影響，近斷層脈沖地震動對矮塔斜拉橋的橋塔位移、橋墩位移和內力以及主梁橫向位移的參數敏感性影響較大，而主塔剪力、主塔彎矩和主梁豎向位移參數敏感性在近斷層地震動下影響不顯著。

Yoshida [9]等提出了可用于有限元分析的本構模型，此模型由兩部分構成，即以應變為基礎的彈塑性部分和與應力為基礎的超彈性部分。Grant[10]等以逆向思維，提出了忽略速度相關性的理論模型，該模型是基于橡膠支座受到水平剪切作用力時的擬合模型。

從總體上看，以前部分學者的研究思路都是在雙折線模型基礎上考慮位移增量來實現支座速度相關性問題，通過各種數學思路來擬合支座的滯回曲線，得到一個相對能實現支座速度相關性的力學模型，再運用于有限元分析中，通過具體實例來說明和論證提出模型的合理性和準確擬合性。本論述在前人的基礎理論研究上，將進一步對超高阻尼支座運用于連續剛構矮塔斜拉橋邊墩的力學性能和位移特性做進一步分析，為超高阻尼支座用于工程實踐提供實際工程數據依據。

1工程背景

渭河五號矮塔斜拉橋橋址位于甘肅天水，主墩采用雙薄壁柔性墩消除部分動力響應能量，總體布置為三跨連續剛構矮塔斜拉橋，橋跨布置為75+126+75m，墩身厚1.0 m，塔高20 m，邊墩采用矩形柱式墩，墩身厚2.0 m，連續剛構橋梁是由橋跨結構主梁和墩臺整體相連的橋梁，主墩、橋塔與主梁剛性連接。在建階段工程如圖1所示。

2有限元建模

采用 Midas Civil 2019v2.2建立有限元全橋模型，模型示意圖如圖2所示。采用一般梁單元模擬主梁、墩、承臺和樁基，桁架單元模擬斜拉索，主梁與主墩之間采用剛性連接固結使塔墩主梁固結，承臺與主墩采用剛性連接，全橋882個節點、806個單元，雙面斜拉索以雙倍單索輸入作用于梁單元，斜拉索與梁采用彈性連接。邊墩的雙肢柱式墩，分為普通支座和超高阻尼橡膠支座。

（1）支座布置

連續梁橋兩端邊墩與引橋連接點位置處設置超高阻尼支座，采用矩形超高阻尼支座，支座截面為矩形，如圖3所示。支座布置于橋梁邊墩處，如圖4所示。一般而言，超高阻尼支座的阻尼添加劑的阻尼系數在超高阻尼橡膠支座的阻尼比大于18%（普通高阻尼橡膠支座為12%左右）。超高阻尼橡膠隔震支座兼有隔震裝置和阻尼器的作用，在隔震系統中獨立使用。

（2）支座力學性能和模擬

根據模型初步運行計算，上部結構恒載梁端最大支承反力為8451.2 kN，由于邊墩為雙支墩，所以選擇不超過支承反力為4225.6 kN的支座承載力。根據規范《橋梁超高阻尼隔震橡膠支座》JT/T 928-2014[11]，選擇的有關支座參數見表1～表2所列。

由規范《橋梁超高阻尼隔震橡膠支座》（JT/T 928-2014）[11]得出支座的第一、第二形狀系數分別為 S1=9.625、S2=7.411。取剪切彈性模量 G=1.0 MPa，由此計算得出豎向剛度 E=684.0258 MPa，從而得出支座豎向剛度Kv=5069.486 kN/mm。

（3）樁基礎模擬

樁基礎的水平剛度采用梁單元模擬，樁土效應使用“m”法計算樁基土彈簧的水平向剛度。由公式（1）計算得出：

K = m ?c ?a ?z ；????????????????????? （1）

式中：K 為土彈簧計算剛度；m 為土層系數；a 為樁基的有效寬度；c 為所計算土層的厚度；z 為土層深度。

3地震參數擬合

3.1地震波初選

順橋向地震波與橫橋向的三條地震波的放大幅值見表3所列。

選擇 Midas Civil 既有地震波james_v、pacoimal以及人工合成波通過調整最大峰值加速度，得出設置同樣的地震動峰值加速度為0.3 g 和地震動加速度反應譜特征周期為0.4 s 的三條波的模型加載內力位移響應最大值對應的地震波，進行減隔震和非減隔震結構對比。人工擬合地震的地震波時程函數如圖5所示。

地震波參數選取按照規范《公路橋梁抗震設計細則》（JTG/T B02-01-2008）的標準進行選擇，選擇 E2地震抗震規范計算，選取60 s 的計算時間，最大迭代次數為60。

3.2不同地震波作用結果

得到橋梁結構邊墩墩底、中墩墩底和塔底的內力圖以及邊墩墩頂、中墩墩頂和塔頂的位移圖，結構在三條地震波作用下，結構關鍵位置不同方向剪力、彎矩和位移如圖6～圖11所示。

由圖6～圖11可知，在中墩墩頂，人工合成地震波作用的橫向最大位移較James_v地震波作用的橫向最大位移高13.4%，較Pacoimal地震波作用的橫向最大位移高2.8%。類似，塔頂位置的人工合成地震波作用的最大橫向位移較James_v和Pacoimal地震波作用的最大橫向位移高11.5%和3.9%，邊墩墩頂最大橫向位移的差值分別為26.3%、8.1%。選取人工擬合地震波較為符合最大內力位移條件。

4超高阻尼支座動力特性分析

4.1自振模態振型特性

特征值分析選擇多重 Ritz 向量法分析，地面加速度 X、Y、Z 向計算向量數量分別為30，得到結構前五階振型形狀如圖12所示。

由橋梁振型模態圖得到各模態的振型描述，見表4所列。

由表4可知：對于頻率而言，一階～五階振型模態的頻率呈遞增趨勢。X 方向振型參與質量在第二、三階模態達到83.39%和99.55%，振型參與質量較為充分，取對應的周期0.652和0.469參與荷載工況中的阻尼計算，并且在阻尼計算中取0.03的初始阻尼比。

4.2支座滯回曲線

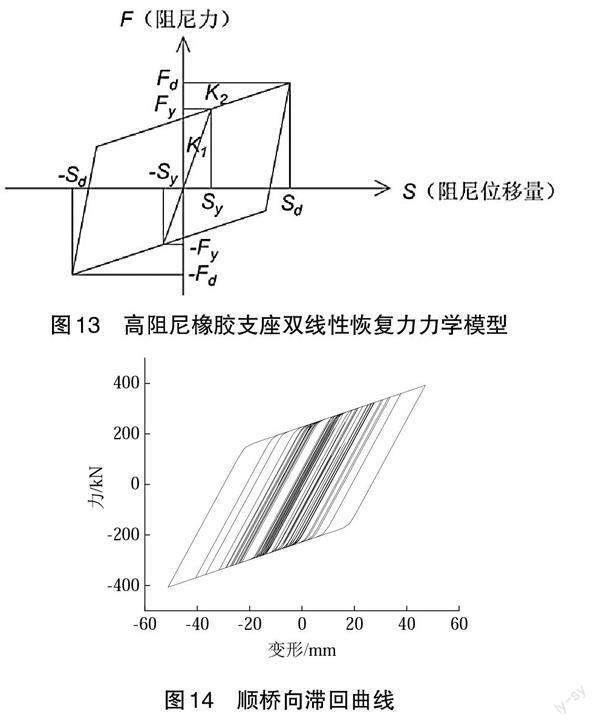
本論述擬結合采用超高阻尼橡膠支座的橋梁結構進行地震響應分析，得到橋梁結構受高阻尼橡膠支座參數的影響規律以及高阻尼橡膠支座的減震耗能效果。經過各模擬參數的規范合理擬合，得到實際的滯回曲線和理論滯回曲線進行對比，各方向的滯回曲線理論與擬合結果 F—L，如圖13～圖14所示。

由圖14可以看出，在雙向地震波作用下，減隔震支座水平設計位移在±50 mm 左右，等效剛度等參數均設置較為合理，這與理論滯回曲線吻合。

4.3雙向地震響應的結構內力變化

選取三個位置：中墩墩底、邊墩墩底和塔底進行不同結構的內力變化分析。

通過式（2）進行定量對比：

由圖15可知，不論添加減隔震支座與否，縱向彎矩和縱向剪力的最大位置均為中墩墩底，在順、橫橋向地震波組合下，中墩墩底位置的最大縱向彎矩和最大縱向剪力為邊墩墩底和塔底內力的2～3倍。添加減隔震支座后，中墩墩底位置的縱向最大彎矩減隔震率為34.7%，即邊墩處設置減隔震支座對中墩墩底的縱向最大彎矩影響較大，設置超高阻尼支座位置的邊墩處，縱向最大彎矩減隔震率為31.7%，隔震效果較強，對于受地震波影響較大的塔底而言，縱向最大彎矩減隔震率為21.6%。

由圖16可知，對于邊墩，墩底橫向最大彎矩具有58.3%的隔震率，不論減隔震結構抑或是非減隔震結構，中墩墩底橫向最大彎矩是邊墩墩底和塔底的3～10倍。設置減隔震結構后，對中墩墩底橫向彎矩有一定影響，其減隔震率為8.3%。從設置減隔震支座的邊墩角度出發，相對于橫向最大彎矩，達到了良好的減隔震效果。對比縱向內力和橫向內力發現，在地震動響應時，減隔震與非減隔震支座的縱向最大彎矩和剪力均達到最大值，隨后，超高阻尼支座的阻尼劑發生作用，所以此處減隔震支座縱向內力的減隔震率沒有橫向內力的減隔震率高。總體受力仍然具有較好的減隔震效果。

4.4雙向地震響應的結構位移變化

取同樣的3個工程關鍵位置：中墩墩頂、塔頂和邊墩墩頂為細部研究對象，分析計算后得出3個位置的具體數值，與非減隔震結構進行位移的各向對比，得到各位置的減隔震率。

（1）由圖17可知，以順橋向地震為主的組合波作用，縱向位移明顯高于橫向位移，這是因為橋梁橫向跨度37 m，本身具有很大的剛度。

（2）在減隔震支座作用下，中墩墩頂位置的縱向最大位移減隔震率達到32.7%，塔頂位置的縱向最大位移減隔震率達到32.6%，而設置減隔震支座的主要位置邊墩，其減隔震率達到44.4%。對縱向最大位移而言，超高阻尼支座對整座橋梁結構減隔震效果貢獻較大。

5結論

（1）橋梁前三階自振模態的振型參與質量達到了83.39%和99.55%，得到超高阻尼橡膠支座的力學各向滯回曲線，將其和理論滯回曲線相對比，以此反證超高阻尼橡膠支座的模擬參數合理性。

（2）支座所在的邊墩處，其墩底位置縱向彎矩減小了31.5%，此位置的橫向彎矩減隔震率達到58.3%，邊墩墩頂縱向位移的減隔震率為44.4%，橫向位移減隔震率為72.3%，邊墩墩底位置的縱向剪力減隔震率為5.9%，橫向剪力減隔震率達到34.6%，總體的減隔震率較大，減隔震效果明顯。

（3）中墩墩底縱向彎矩減隔震率為34.7%，橫向彎矩減隔震率為8.3%，橫向剪力為6.4%，從位移角度出發，此位置的墩頂縱向位移減隔震率為32.7%，橫向位移減隔震率為9.2%，說明在雙向地震波組合作用下，減隔震支座對中墩位置的縱向位移折減較大，對橫向位移減隔震效果不明顯，總體減隔震效果呈正向分布，但邊墩位置的支座性質變化對主墩的橫向內力與橫向位移影響不大。

（4）對比非減隔震結構，塔底縱向彎矩和縱向剪力的減隔震率分別為21.6%、27.5%。塔底橫向彎矩和橫向剪力的減隔震率分別為35.9%、41.6%。塔頂縱向位移和橫向位移的減隔震率分別為32.6%、10.8%，縱向位移減隔震率突出，橫向位移減隔震效果不明顯。從內力角度出發，減隔震支座對整體橋塔的減隔震效果非常明顯。

參考文獻：

[1] 莊學真，沈朝勇，金建敏.橋梁高阻尼橡膠支座力學性能試驗研究[J].地震工程與工程振動，2006，26（5）：208-212.

[2] 袁涌，朱昆，熊世樹，等.高阻尼橡膠隔震支座的力學性能及隔震效果研究[J].工程抗震與加固改造，2008，30（3）：15-20.

[3] 沈朝勇，周福霖，崔杰，等.高阻尼隔震橡膠支座的相關性試驗研究及其參數取值分析[J]. 地震工程與工程振動，2012，32（6）：95-103.

[4] 陳彥江，郭凱敏，李勇，等.橋梁高阻尼隔震橡膠支座性能試驗研究[J].振動與沖擊，2015，34（9）：136-140，148.

[5] 劉涵，彭凌云，孫天威，等.阻尼支座對混凝土框架樓梯抗震性能影響的試驗研究[J].振動與沖擊，2022，41（12）：188-195.

[6] 臺玉吉，孫呈凱，許賀淇.地震作用下大跨連續梁橋隔震支座研究[J].工程抗震與加固改造，2021，43（5）：96-103.

[7] 萬樂樂，季日臣，夏修身.大跨度高速鐵路矮塔斜拉橋減隔震設計研究[J].鐵道建筑，2021，61（12）：31-35.

[8] 王偉軍，虞廬松，王力，等.基于神經網絡的矮塔斜拉橋近斷層地震響應參數敏感性分析[J].中國安全生產科學技術，2022，18（6）：111-118.

[9] Yoshida J，AbeM，Fujino Y. Constitutive Model of HighDamping Rubber Materials[J]. Journal of Engineering Me?chanics，2004，130（2）：129-141.

[10] Grant DN，FenvesGL，Whittaker AS. Bidirectional Model?ling of High- Damping Rubber Bearings[J]. Journal ofEarthquake Engineering，2004，8（1）：161-185.

[11] 中華人民共和國交通運輸部.橋梁超高阻尼隔震橡膠支座：JT/T 928-2014[S].北京：人民交通出版社，2014.