基于PSO-SVM算法的空氣質量分類研究

龐 曦，胡榮華，趙春生，白寧波

（1.永城煤電控股集團有限公司，城郊煤礦，河南 永城 476600；2. 中國地質大學，湖北 武漢 430074）

0 引言

目前，人們在生產生活中對空氣污染的預防以及城市管理層出臺治理空氣污染的有關政策均是依據氣象部門給予的空氣污染等級，因此對空氣質量等級進行精準劃分對當今社會的安全發展有著重要的現實性意義[1-2]。

為了精確地對空氣質量進行分類預測，很多學者對此做了深入研究。例如：邱晨提出了基于BP神經網絡的空氣質量模型分類研究方法[3]；常麗娜提出了基于K-均值聚類和貝葉斯判別的城市空氣質量等級分類及預測方法[4]；王琛提出了哈夫曼樹SVM在空氣質量等級分類中的應用方法[5]等。上述方法均能對空氣質量進行有效分類，但受限于算法本身的局限性，其分類效果還有待提升。例如：BP神經網絡收斂速度慢，其算法精度依賴于大量的訓練樣本并在訓練過程中極易陷入局部最優解[6]；K-均值聚類預測法需要事先給定聚類的種類數即K的取值，K值在實際應用中是難以估計的，K值偏大或者偏小都嚴重影響分類的精確度。本文通過分析空氣質量分類的特點和現有分類方法的不足，提出了粒子群優化支持向量機算法的空氣質量分類方法[7]。

選用某礦區全年在空氣中測量得到的PM2.5、PM10、SO2、NO2、CO、O3數值指標組成六維輸入向量，以空氣質量的指標優良、輕度污染、中度污染和重度污染作為輸出向量，結合PSO優化算法在分類模型訓練中全局搜尋SVM的最佳參數c和gamma，然后將最佳參數應用到空氣質量的分類預測中，能夠大大增加分類預測的準確性。

1 SVM算法原理

SVM分為線性可分和非線性可分，其基本原理是將低維空間的樣本訓練數據映射到高維空間中，使得樣本訓練數據線性可分，進而對邊界進行線性劃分[8-9]。如果有樣本數據：其中xi是輸入指標，yi是輸出指標，其分類示意圖如圖1所示。

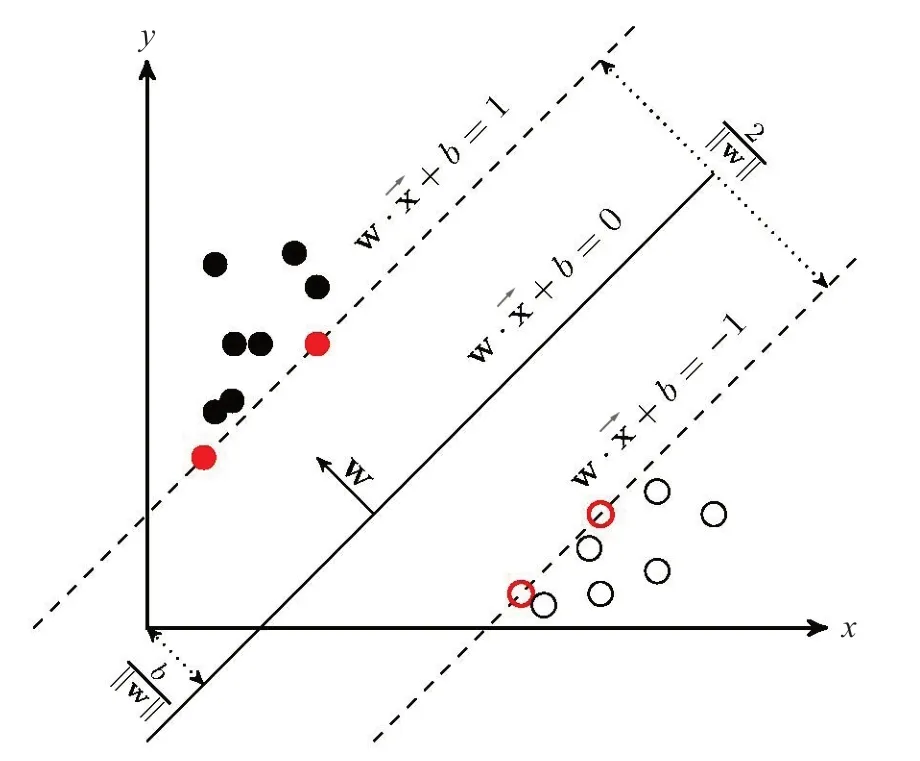
圖1 SVM二分類示意圖

對于二分類問題實際就是尋找區分兩類數據的最優分割超平面，超平面方程如式（1）：

選擇合適的w、b使距離超平面最近的樣本滿足得到規范化超平面，當分類間隔達到最大時確定最優超平面[10]，如式（2）：

若要使得所有樣本都分類無誤，根據約束條件應滿足式（3）：

在式（3）中引入拉格朗日算子ai構建函數，其中ai＞0，將有約束的原始目標函數轉換為無約束的拉格朗日目標函數，如式（4）：

求L對w、b的偏導，令其等于0，得到一個包含ai的函數，如式（5）：

求得w、a、b對應的最優解w*、a*、b*，獲得最優分割超平面，如式（6）：

確定SVM的分類決策函數如式（7）：

2 PSO-SVM算法原理

2.1 粒子群優化算法

粒子群優化算法的本質就是迭代尋優，通過撒下的粒子種群更新其位置和運動速度在全局尋找適應度函數的最優解[11]。假設在一維目標搜索空間中，由N個粒子組成群體X的初始位置為得到初始局部最優為P1，然后更新粒子的搜尋速度和位置，在時刻t，該種群粒子更新位置至該粒子種群中局部最優位置表示為P(t)，t時刻的粒子群的局部最優位置為與初始局部最優位置相比較得到全局最優位置g(t)，然后繼續迭代更新粒子的搜尋速度與位置，每更新一步都要對比得到最新的局部最優和全局最優，直至達到最大迭代次數為止。當粒子種群在M維目標搜索空間內，粒子群的速度與位置更新公式如（10-11）：

2.2 PSO-SVM算法流程

SVM在運行前需要手動設置兩個參數：其中c是懲罰系數，即對誤差的容忍度，c值高說明誤差容忍度小，容易過擬合，c值越小容易欠擬合；gamma是核函數自帶的一個參數，決定了數據映射到新的特征空間后的分布，gamma越大，支持向量越少，gamma值越小，支持向量越多，支持向量的個數影響訓練與預測的速度[12-13]。

為了消除人為設置參數c和gamma對SVM運行的影響，使用PSO算法在全局搜尋c和gamma的最佳參數組合，具體的PSO-SVM算法流程見圖2。

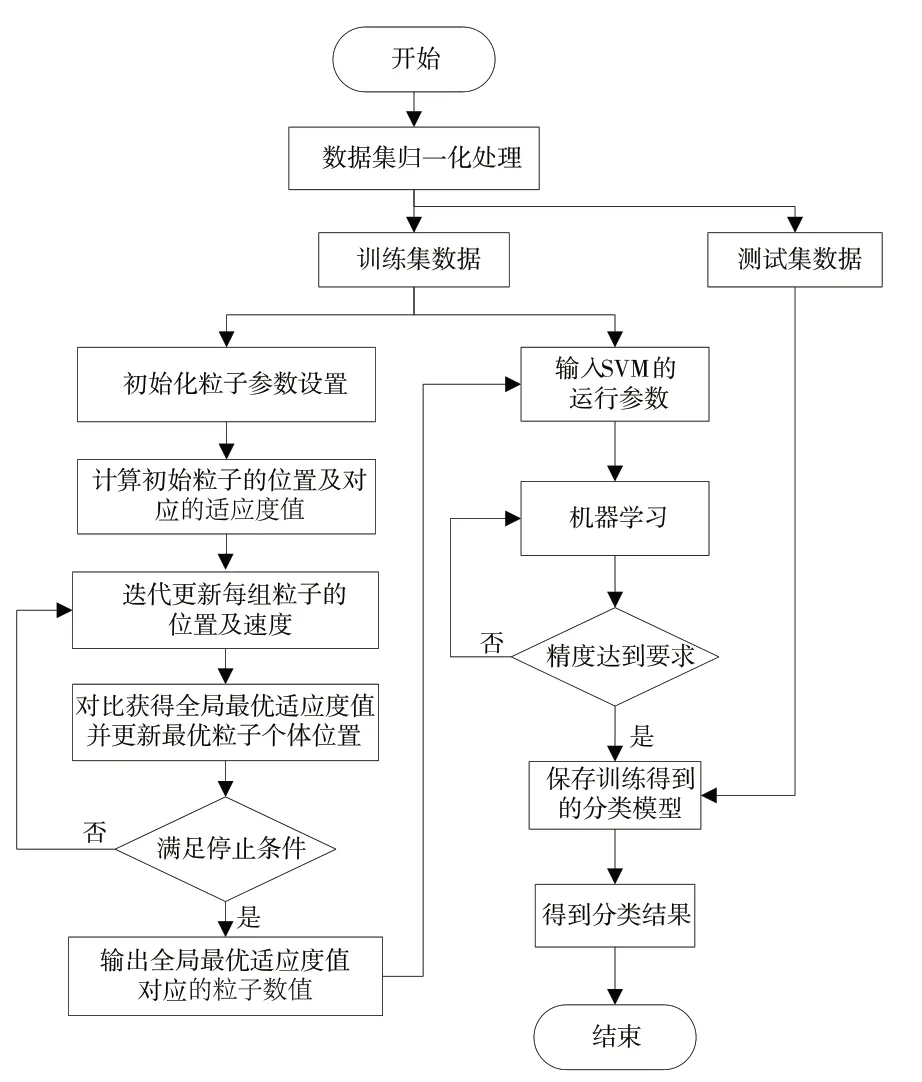
圖2 PSO-SVM算法流程圖

3 算例分析

選擇某礦區一年度在空氣中測得的PM2.5、PM10、SO2、NO2、CO、O3的數字指標組成六維輸入向量，以空氣質量的指標優良、輕度污染、中度污染和重度污染作為輸出向量。其中優良的標簽為1，輕度污染的標簽為2，中度污染的標簽為3，重度污染的標簽為4。選擇其中150組為訓練數據，分別訓練得到SVM分類模型、PSO-SVM分類模型，其余215組為測試數據，使用測試數據的分類準確率來評價分類模型的性能。

3.1 數據預處理

在選擇輸入向量的同時，為消除數據物理量綱的不同和盡量壓縮數據大小的范圍，以增加運行的速度，需要對數據進行歸一化處理，數據歸一化公式如（12）：

壓縮后典型的輸入、輸出向量如表1所示：

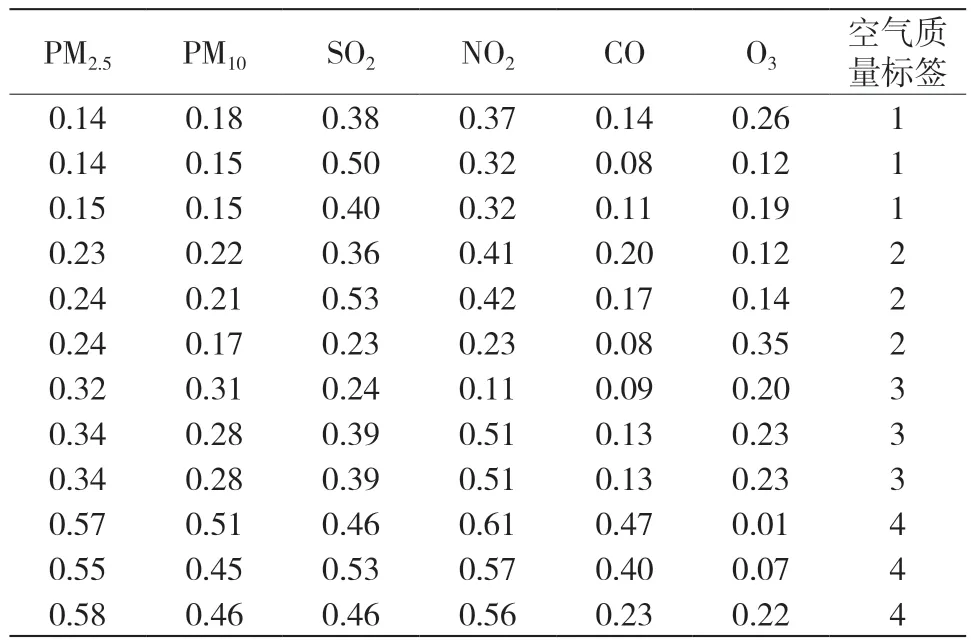
表1 幾種典型的輸入輸出向量

從表1看出，不同空氣質量之間的特征向量區別度非常大，尤其是PM2.5和PM10，隨著空氣質量的逐漸劣化其數值也不斷增加。相比較而言，其余的特征量區分度雖然沒有這么明顯，但不同的空氣質量所對應的數值也有著明顯區別。

3.2 SVM分類模型建立

針對SVM多分類問題需要設置核函數，常用的核函數有四種，分別是線性核函數、多項式核函數、RBF核函數、sigmoid核函數。使用每個核函數訓練數據都會得到不同的分類模型，然后將分類模型的輸出結果與訓練集數據原始標簽相比較，表征四種核函數對輸入數據的擬合率，擬合率越高說明此核函數越適合于此類數據的分類預測。訓練數據共有150組，其中優良、輕度污染、中度污染和重度污染分別為60、60、10、20組，設置SVM的運行參數c和gamma為100和10，設置目標精度為0.001。使用4種核函數分別對訓練數據集進行分類模型訓練，并對分類模型的輸出結果與訓練集數據原始標簽進行對比，得到4種核函數對應的擬合率如表2。

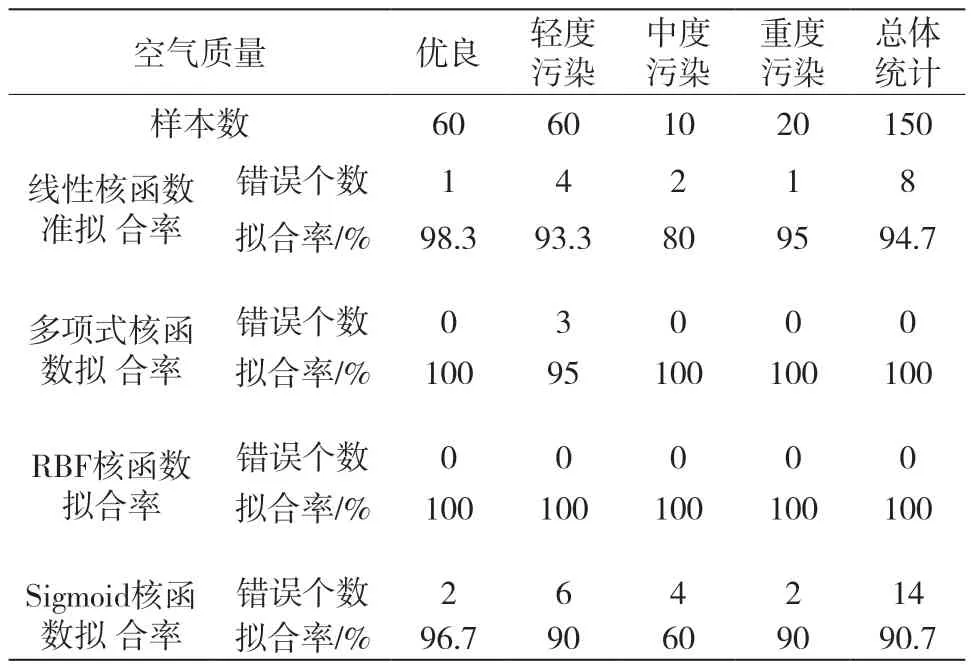
表2 4種核函數訓練模型對應的準確率

從表2中的準確率可以看出，對于本次數據處理的適用性： RBF核函數＞多項式核函數＞線性核函數＞sigmoid核函數，使用RBF核函數訓練得到的分類模型有著更高的擬合率，接下來的SVM分類模型均采用RBF核函數，RBF核函數公式如式（13）：

3.3 PSO-SVM分類模型建立

PSO-SVM算法的目的就是使用PSO算法在全局進行尋優，找到最佳的參數組合c和gamma，然后將最佳參數組合使用在SVM分類模型訓練中，增加SVM分類模型在分類預測中的準確率，使用PSO算法需要設置一個適應度函數，作為粒子群迭代尋優的目標函數。本文采用分類預測結果與測試集數據原始標簽的均方誤差作為適應度函數[14-15]，均方誤差如式（14）：

式中：P—分類預測結果，Y—測試集數據原始標簽，length（Y）—測試集數據原始標簽的長度。均方根誤差值越小說明分類模型的分類預測準確率越高，PSO算法運行前需要設置算法的初始參數，設置粒子種群加速因子C1=C2=1.5、慣性權重w=0.7、粒子種群規模為20、最大迭代步數T=300、粒子搜尋空間范圍為[1, 1000]，初始速度v=10，粒子群的迭代尋優過程示意如圖3所示。

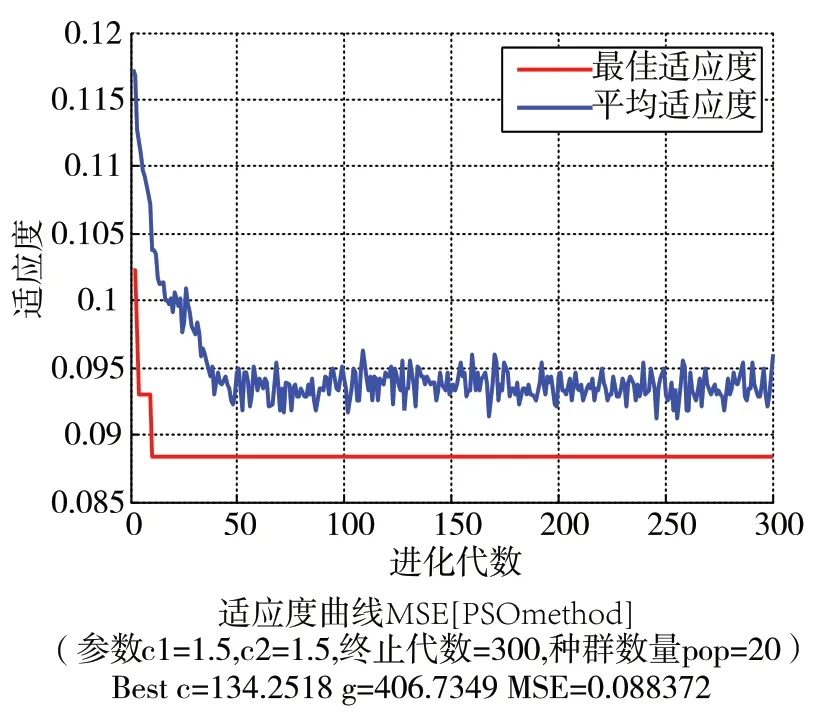
圖3 粒子群迭代尋優示意圖

從圖3中可以看出，粒子群迭代10步之后搜尋到了適應度的全局最優值，此時MSE=0.088，c=134.25，g=406.73，每步迭代后的平均適應度值也一直逼近全局最優適應度值，說明每次迭代粒子種群都在朝著最優的位置運動。

3.4 預測結果及分析

使用SVM分類模型和PSO-SVM分類模型分別對215組測試集數據進行分類預測，其中優良、輕度污染、中度污染和重度污染分別為120、56、15、24組，分類預測結果分別如圖4、圖5所示。

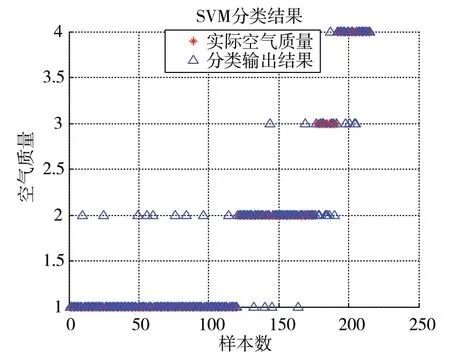
圖4 SVM分類模型輸出結果

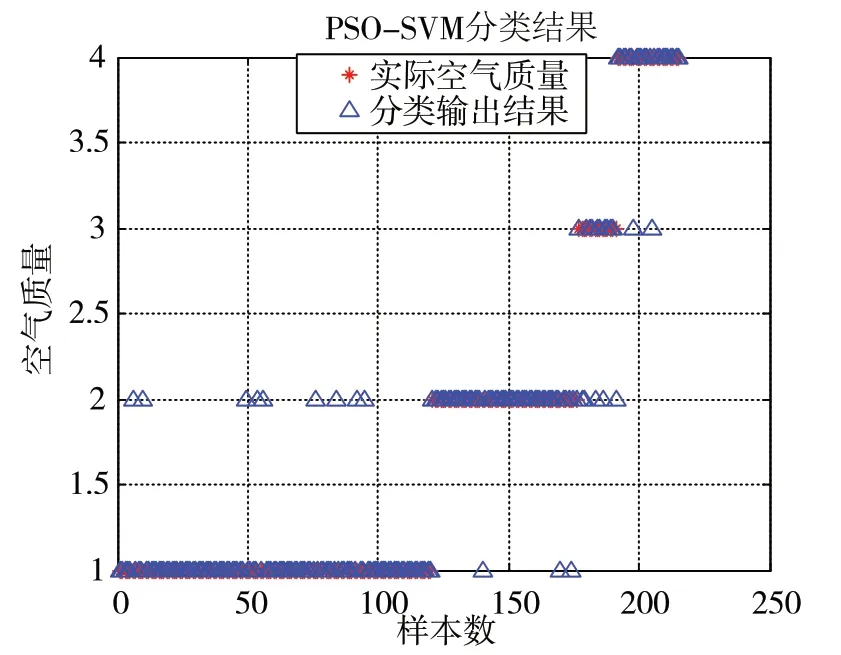
圖5 PSO-SVM分類模型輸出結果

圖4、圖5顯示，SVM分類模型分類正確188個樣本、錯誤27個樣本，整體分類正確率為87.44%。其中：優良樣本分類正確111個，錯誤9個，分類正確率為91.75%；輕度污染分類正確50個，錯誤6個，分類正確率為89.29%；中度污染分類正確8個，錯誤7個，分類正確率為53.33%；重度污染分類正確20個，錯誤4個，分類正確率為83.33%。PSO-SVM分類模型分類正確196個樣本，錯誤19個樣本，整體分類正確率為91.16%。其中：優良樣本分類正確111個，錯誤9個，分類正確率為91.75%；輕度污染分類正確53個，錯誤3個，分類正確率為94.64%；中度污染分類正確10個，錯誤5個，分類正確率為67.67%；重度污染分類正確22個，錯誤2個，分類正確率為91.67%。

從分類預測結果可以看出，PSO-SVM分類模型與SVM分類模型相比較總體分類正確率提高了3.72%，不同的空氣質量樣本正確率也有著較大的提高。其中：輕度污染的分類正確率提高了5.35%，中度污染的分類正確率提高了14.34%，重度污染的分類正確率提高了8.34%。

4 結論

（1）采用PM2.5、PM10、SO2、NO2、CO、O3的數值指標組成的六維特征向量，能夠有效的表征空氣質量的等級。

（2）通過對SVM分類算法的訓練，得到的分類模型能夠對空氣質量等級進行分類，但是分類準確率還有待提高。

（3）PSO優化算法能夠以迭代尋優的方式在全局搜尋SVM的最佳參數c和gamma，使得此時的適應度函數達到最優。

（4）PSO-SVM算法能夠對空氣質量等級進行分類，且相比較SVM分類算法，其分類正確率有著大幅度的提高。