水平管道過冷沸騰換熱的非穩態數值計算

劉 征,余志毅,2,孫偉華,張 珂

(1.北京理工大學 機械與車輛學院,北京 100081;2.水沙科學與水利水電工程國家重點實驗室(清華大學),北京 100084)

過冷沸騰是指壁面溫度高于飽和溫度,液體主體溫度低于飽和溫度下所發生的局部沸騰現象,作為一種強化換熱方式應用于內燃機、電子元器件、充電電纜、車用電池以及大功率激光武器等重要設備的散熱[1-7]。有學者針對過冷沸騰流動換熱進行了大量數值計算方面的研究,可以分為兩方面:一類是穩態計算,這類計算的計算量較小,一般針對相對復雜的結構,只能獲取各參數的結果分布[5-10];另一類是同時反映參數分布規律和瞬時特性非穩態計算,側重于對流動過程參數的獲取,計算量較大,更能接近實際沸騰過程。魏敬華等[11]對豎直窄縫通道內的過冷流動沸騰進行了數值計算研究,分析了不同壓力和熱流密度下的汽泡動力學特性;潘良明等[12]建立了過冷流動沸騰凝結模型,以分析汽泡凝結過程的流場特性;葛蘇槿[13]從含氣率、物理場、汽泡行為等方面對一傾斜管道內過冷沸騰換熱特性進行了數值研究;Lee等[14-17]針對垂直管道內FC-72的過冷沸騰進行了大量研究,首先研究了上升流中的高過冷度核態沸騰,總結了換熱系數沿軸向的變化規律,提出了一種適用于VOF模型的剪切力計算方法,并研究了高過冷度沸騰在CHF點前后的流動傳熱特性以及微重力條件下的低過冷度沸騰中的汽泡行為和流型演化;Yeo等[18]在不涉及蒸干的情況下成功模擬了微通道中的過冷沸騰,通過與實驗以及經驗關聯式驗證了數值計算方法的有效性;Chen等[19]對矩形微通道的過冷沸騰進行了數值模擬,分析了含氣率和熱流密度對換熱的影響;曹濤濤[20]基于水平通道中的過冷沸騰,提出了確定Lee模型中傳質系數的經驗關聯式。

現有研究中針對過冷沸騰換熱過程換熱參數波動和分布規律方面的研究較少,實際上換熱參數的波動和分布是氣液相變換熱設備設計的重要依據,參數波動過大產生的熱應力會降低換熱設備的可靠性,而換熱參數的分布規律是確定換熱設備幾何尺寸的重要參考。基于此,針對一宏觀尺度中小直徑水平管道內的過冷沸騰換熱過程進行非穩態數值計算,分析沸騰過程中流動和換熱參數的分布及波動特性,并對過冷沸騰換熱的規律進行總結,為新型換熱設備的相關設計提供借鑒經驗。

1 物理模型及網格劃分

參考目前應用廣泛的換熱設備(如閉式冷卻系統中的冷卻水套以及板翅式換熱器)的通道高度,利用ICEM_CFD 2020 R2建立了一個高度為10 mm的水平管道二維模型,如圖1所示。管道總長為800 mm,其中入口段200 mm,加熱段100 mm,出口段500 mm。采用下壁面加熱方式,底部加熱面與流固耦合面之間的固體域厚度為0.5 mm。

圖1 物理模型及計算域網格分布

通過ICEM_CFD軟件對計算域劃分4套網格,網格總數分別為65 950、107 250、225 000、274 000。選擇基準工況,以加熱壁面固體域的平均溫度作為檢驗標準。計算發現,當網格總數在225 000以上時,加熱壁面固體域的平均溫度變化幅度已經很小。綜合考慮計算量與計算精度,最終選擇第3套網格,即總數為225 000的網格,其中,流體域縱向網格數為65,橫向網格數為3 600,對加熱段、出口延伸段前部以及壁面附近的網格進行加密,第1層網格高度為0.05 mm,YPlus值為3.78。

2 計算模型及設置

2.1 計算模型的選取

VOF多相流模型是一種針對兩種或兩種以上流體的界面跟蹤技術,其優勢是能夠清晰地捕捉到兩相之間的交界面。為了更準確地捕捉汽泡的生成發展過程,分析汽泡的運動規律,選擇VOF模型對過冷沸騰換熱過程進行計算。

湍流模型選擇SSTk-ω模型,湍流阻力因子設置為10,以對壁面處的汽泡生成發展的非穩態過程進行更好的描述[21]。

此外,相變模型是過冷沸騰數值計算所涉及的重要模型。由Lee在1980年提出的半隱式傳熱傳質模型——Lee模型[22],是目前應用最為廣泛的相變模型。該模型將相變過程簡化為飽和溫度與實際溫度的溫差驅動的傳質過程,其形式簡單且能夠模擬沸騰和凝結過程的全階段,Lee模型的基本方程如下[21-22]:

連續方程為

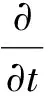
(1)

Lee模型相變過程質量傳遞源項求解方式為

(2)

能量傳遞源項為質量源項與汽化潛熱的乘積,表示為

Q=mhfg

(3)

式中:α為相體積分數;ρ為密度,kg/m3;v為速度矢量;Q為能量傳遞源項,J/(s·m3);m為質量傳遞源項,kg/(s·m3);hfg為汽化潛熱,J/kg;T為流體溫度,K;Tsat為飽和溫度,K;r為相變傳質系數,s-1,其取值需要根據具體工況進行調整,本研究所采取的方式為結合計算關聯式的結果對傳質系數的取值進行若干次試算,最終在3種不同熱流密度(150、200、250 kW/m2)下,汽化傳質系數分別確定為0.1、0.5、2.0。鑒于氣相密度較低,一般認為凝結傳質系數應當取較大值,Kim等[23]認為凝結傳質系數應當在汽化傳質系數的基礎上乘以液體密度與氣體密度的比值,以此為基礎,近似將汽化傳質系數與凝結傳質系數的比確定為1/1 600,故凝結傳質系數的取值分別為160、800、3 200;下標v和l分別代表氣相和液相,下標e和c分別代表汽化和凝結過程。

此外,基于核沸騰起始需要一定的過熱條件,通過UDF功能將Bergles提出的沸騰起始點計算關聯式[24]嵌入由Lee模型構建的傳熱傳質源項表達式中,計算沸騰起始階段所需過熱度,作為計算沸騰核化前單相液體換熱的補充,計算關聯式為

(4)

式中:p為絕對壓力,Pa;qONB為沸騰起始點熱流密度,W/m2;TONB為該熱流密度下所對應的沸騰起始點溫度,K;TONB-Tsat即所在位置達到沸騰起始點所需過熱度,沸騰起始點溫度通過所在位置相鄰接觸面的局部熱流密度以及所在位置的局部壓力求得。

基于此,將成核位置限制在靠近加熱面的近壁區,當流體存在一定過熱,但局部區域不存在相界面時,認為該區域處于沸騰核化前的單相階段,由于此時將要發生的汽化過程位于液相內部,近似以沸騰起始點溫度作為此時的汽化溫度,將式(2)的質量傳遞源項修正為

(5)

當沸騰過程存在相界面或發生氣相的凝結過程時,質量源項求解仍使用式(2)。最后,通過Fluent中的UDF功能,將當前質量源項的求解結果引入計算。綜合考慮式(4)和(5),質量源項可以表達為

(6)

2.2 邊界條件和其他設置

邊界條件方面,入口邊界流速為0.4 m/s,過冷度為5 K;出口壓力設置為常壓101 325 Pa;加熱壁面設置3種熱流密度,分別為150、200、250 kW/m2;表面張力的求解采用Brackbill等提出的CSF表面張力模型[25]。

壓力速度的耦合采用SIMPLEC算法。對于標量方程各項的空間離散,壓力采用PRESTO!格式,體積分數采用幾何重構格式,能量和動量采用二階迎風格式,湍動能和湍流耗散率采用一階迎風格式;為保證計算的收斂性,采用可變時間步長,范圍為5×10-6～5×10-4s,限制全局庫朗數為1以下,每個時間步的最大迭代次數設置為50,計算總時長設置為1.2 s。

3 計算結果分析

3.1 結果合理性驗證

數值計算結果的可靠性通過過冷流動沸騰換熱經驗關聯式驗證。常用的沸騰換熱關聯式中適用于過冷沸騰的關聯式包括Chen關聯式、Moles-Shaw關聯式、Shah關聯式的修正形式、Gungor-Winterton關聯式以及Liu-Winterton關聯式等。Chen[26]關聯式作為最早的疊加關聯式,將流動沸騰換熱看作是液相強制對流換熱和核態沸騰換熱兩種機制共同作用,通過兩種機制的線性疊加求解流動沸騰過程的對流換熱系數。此后在Chen關聯式的基礎上衍生出若干更為精確的沸騰傳熱關聯式,如Gungor-Winterton關聯式、Liu-Winterton關聯式等。Gungor-Winterton[27]關聯式在Chen關聯式基礎上針對核態沸騰換熱過程的對流換熱系數求解采用了更精確的Cooper[28]關聯式,針對過冷沸騰考慮了核態沸騰換熱和強制對流換熱驅動溫差不同做出改進,提升了求解精度;Liu-Winterton[29]關聯式與Gungor-Winterton關聯式類似,區別為Liu-Winterton關聯式采用了非線性疊加方式。適用范圍方面,Shah[30]過冷沸騰關聯式的驗證數據多數集中在普朗特數1以下,雷諾數10 000以上; 而Gungor-Winterton關聯式與Liu-Winterton關聯式采用了相同的數據庫,適用于雷諾數為568.9～875 000、普朗特數0.83～9.1的工況范圍[29],可覆蓋本文數值計算的工況范圍。基于以上,選擇了Gungor-Winterton關聯式對數值計算進行驗證,其計算過冷沸騰對流換熱系數的表達式如下:

q=hl(Tw-Tb)+Shpool(Tw-Tsat)

(7)

(8)

(9)

(10)

F=1+24 000Bo1.16

(11)

(12)

式中:q為熱流密度,W/m2;hl為單相對流換熱系數,W/(m2·K);hpool為沸騰換熱系數,W/(m2·K);F為對流換熱強化因子,過冷沸騰不考慮該系數,取值為1;S為沸騰抑制因子;kl為液體熱導率,W/(m·K);d為水力直徑,m;Rel為液相雷諾數;Prl為液相普朗特數;Bo為沸騰數;G為質量流速,kg/(m2·s);pr為對比壓力;M為相對分子質量。

3種熱流密度條件下,數值計算與實驗關聯式計算結果對比如表1所示。可以看出,盡管存在一定偏差,但數值計算與關聯式計算結果具有相同的趨勢,認為當前所計算結果是合理的。

表1 數值計算與Gungor-Winterton關聯式計算結果對比

3.2 過冷沸騰流場的演變與換熱特性波動

以熱流密度q為250 kW/m2的工況為例,流場在計算時間t為0.5 s時刻后到達相對穩定狀態。圖2為該工況下0.7～1.2 s過冷沸騰流場中氣相分布的變化及局部區域矢量圖。可以看出,由于下壁面的加熱,汽泡不斷形成并隨主流向下游運動。總體上看,加熱段的前半部分汽泡較細、較少,處于核化、脫離和初步生長階段,而后半部分汽泡明顯增大,氣泡的合并和消亡現象更明顯。伴隨著汽泡的核化、生長、脫離、消亡等過程,壁面與流體間的換熱受到干擾。如圖2所示,由0.9和1.2 s時刻壁面附近的局部流場圖可見,汽泡的生長和運動等行為對壁面附近流動造成強烈的擾動,并形成明顯的漩渦。這些擾動使得管道換熱面的換熱性能得到強化的同時,將造成換熱特性的波動。

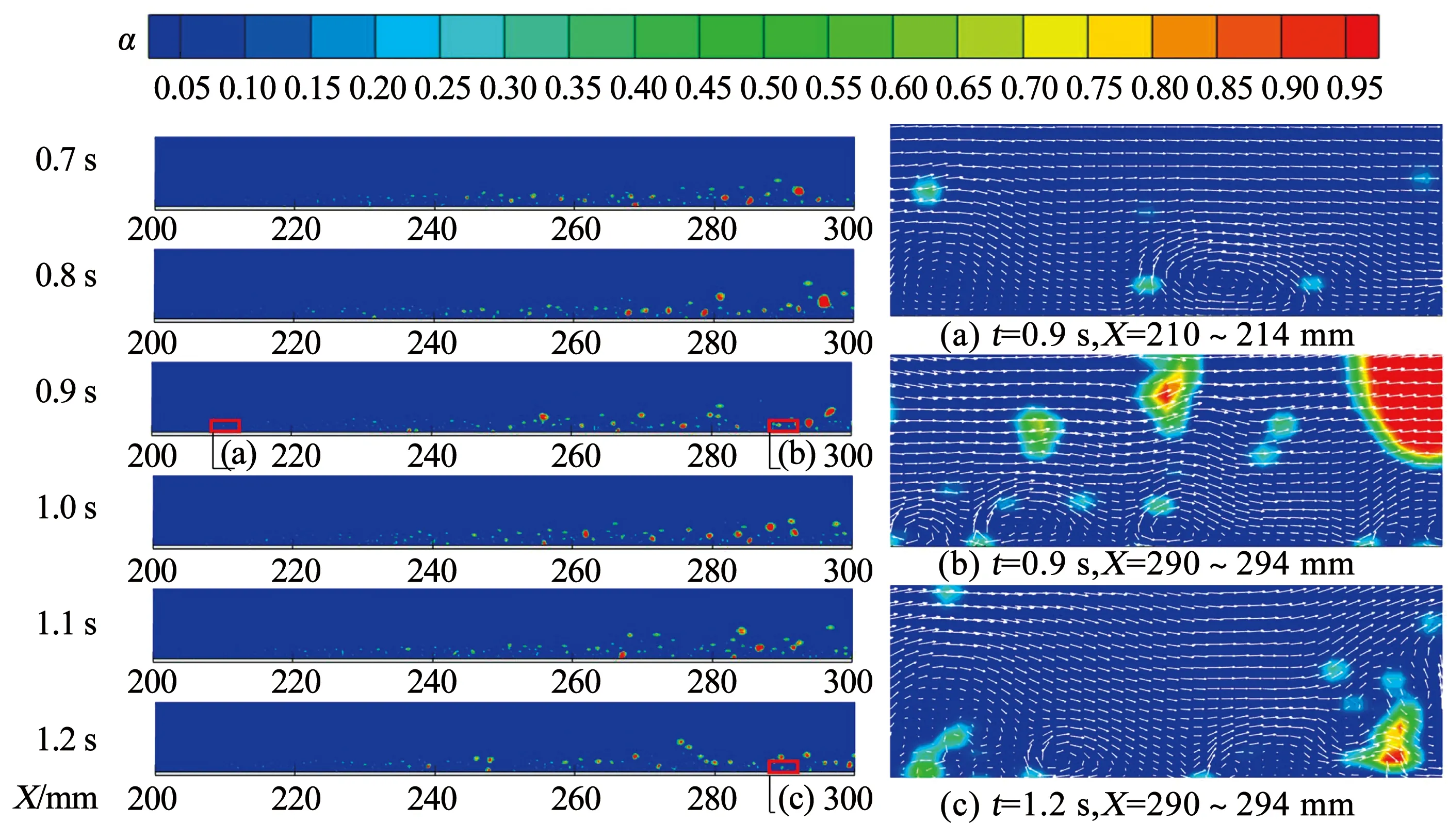
圖2 熱流密度250 kW/m2工況加熱段氣相分布隨時間t的變化及部分局部放大區矢量圖

圖3為與圖2相對應的溫度分布。可以看出,從加熱段進口到加熱段約中間位置,熱邊界層沿流動方向逐漸增厚,此后該厚度無明顯增加,在一均值上下波動。基于此特點,可將管內流動沸騰分為熱邊界層發展段與核沸騰主導段,250 kW/m2工況下兩者的分界線約在橫坐標X等于250 mm處。

在熱邊界層發展段,加熱表面放出的熱量部分用于加熱壁面附近流體,使得該區域流體的溫度逐漸升高,另一部分則通過液體的汽化過程被吸收;當熱邊界層溫度達到飽和溫度,邊界層內熱傳遞逐漸趨向穩定,進入核沸騰主導段,此時,主流區的溫升以及汽化過程使得壁面附近流體溫度隨位置變化相對較小,壁面所放出的熱量主要通過汽化過程被吸收。同時,對比圖2和3可知,核沸騰主導段的流場隨時間的波動更為劇烈,表明沸騰過程增加了流場中的不穩定性。

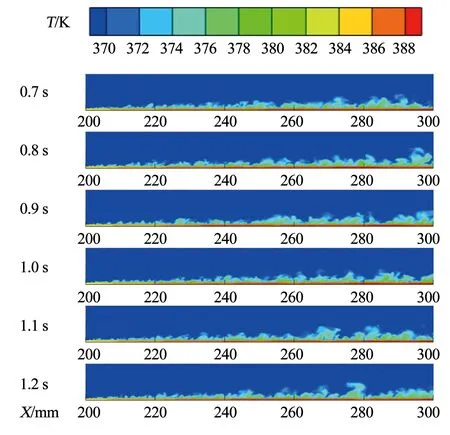
圖3 熱流密度250 kW/m2工況加熱段溫度分布隨時間t的變化

圖4分別為加熱區域各部分對流換熱系數隨時間的波動,每個樣本點為0.05 s時間段內該區域的平均值。對比發現,各段對流換熱系數隨時間均存在波動性,熱邊界層發展段前部的換熱系數波動幅值較小,而其下游區域換熱系數波動幅值沿流動方向整體呈現增加趨勢。造成前者波動趨勢的原因是熱邊界層發展段前部的壁面溫度與近壁面液相溫度較低,顯熱帶走了較多的熱量,受到汽泡核化以及生長脫離過程影響較小,換熱系數波動不明顯,另一方面該段壁溫相對較低,汽泡脫離直徑較小,使得汽泡生長產生熱阻所造成的影響更小,該段各部分的對流換熱系數平均波動幅值小于核沸騰主導段;而下游區域近壁區溫度升高造成壁面換熱特性受汽泡生長脫離周期的影響明顯,對流換熱系數產生明顯波動,受到汽泡脫離直徑增加的影響,波動幅值整體較大。如200～220 mm段在0.5 s記錄時間段內的波動幅值為414.16 W/(m2·K),而>260～280 mm段以及>280～300 mm段的波動幅值分別為1 196.33和815.93 W/(m2·K),>220～300 mm整體平均波動幅值為794.14 W/(m2·K),約為熱邊界層發展段前部波動幅值的2倍,且波動規律相似,表明汽泡的生長運動加劇了對流換熱系數的波動,使得入口區域以外的波動規律具有相似特性。

3.3 熱流密度對過冷沸騰流場的影響

圖5～7分別為t為1.0 s時刻3個工況下的溫度分布、氣相分布以及速度分布,三者之間相互影響。如圖5所示,加熱段熱流密度的變化直接影響加熱段近壁區溫度分布,不同熱流密度下,壁面附近液體溫度升高速度不同,沸騰發生的位置和強度相應不同,對管內速度場產生不同影響。如圖6所示,隨著熱流密度增加,壁面附近出現明顯汽泡的位置提前。q為150 kW/m2工況下壁面附近存在的汽泡數量很少,汽泡的生長、合并與脫離現象很不明顯;與之相對,q為250 kW/m2的工況下汽泡活動范圍得以擴大,其在加熱段前部即產生細泡狀流型,而后由于壁面溫度的升高以及汽泡的生長合并使得其直徑不斷增大。同時,各工況下產生的汽泡對近壁區域流場產生不同程度的擾動,汽化過程造成的膨脹使得下游流速不同程度的升高,如圖7所示,熱流密度越大,產生的汽泡越多,近壁區域流場速度分布越不規則,下游速度越大,其中,流體速度用v表示。

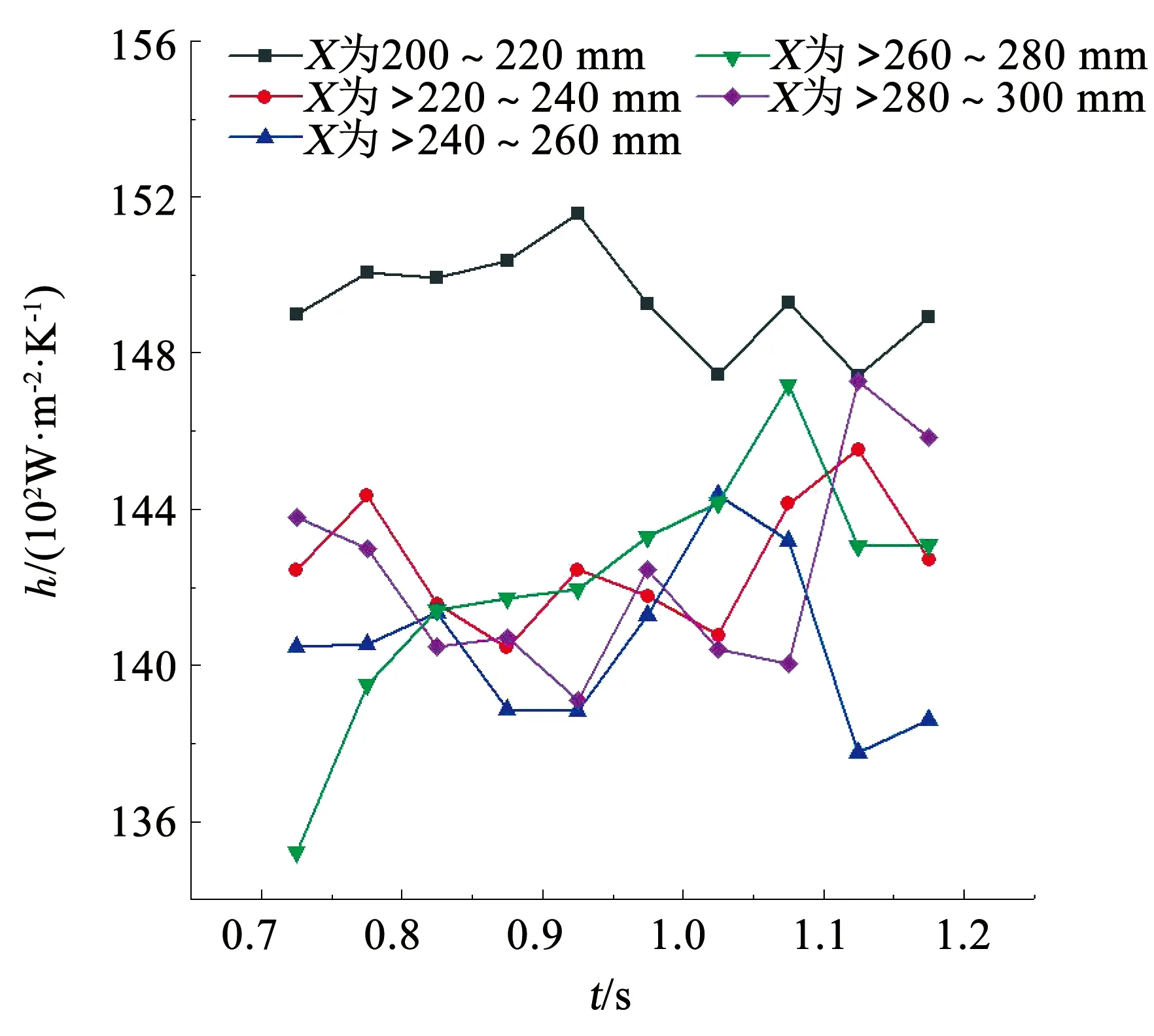
圖5 各工況加熱段溫度分布

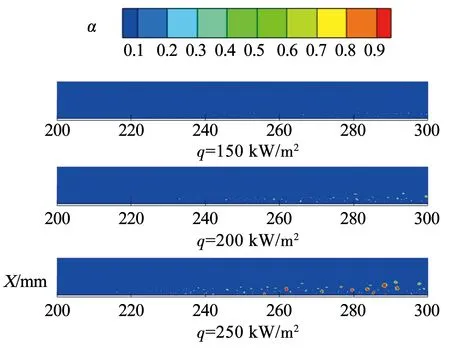
圖6 各工況加熱段氣相分布

圖7 各工況加熱段速度分布

3.4 過冷沸騰對流換熱系數隨位置的變化

由于當前工況水平管道的過冷沸騰是從單相逐漸轉變為兩相,加熱面的對流換熱系數隨流動位置變化,不同工況下對流換熱系數隨位置的變化存在一定差異。

圖8為3個工況下,局部平均對流換熱系數隨位置的變化。與換熱的波動特性類似,造成各局部平均換熱系數變化的原因同樣包含熱邊界層沿流動方向的發展以及沸騰對傳熱的強化兩種機制。

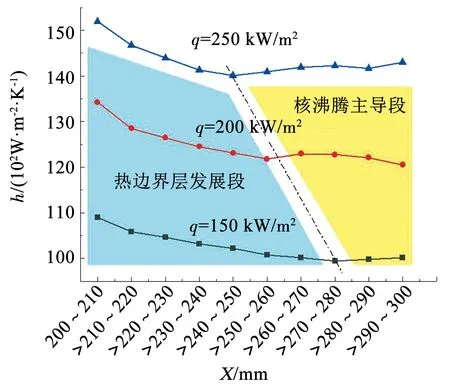
圖8 0.7～1.2 s對流換熱系數h沿水平坐標X的變化

對比圖5可以看出,熱邊界層發展段對流換熱系數沿流動方向不斷下降,熱流密度越大,該區域對流換熱系數沿流動方向變化越快,發展所需通道的長度越短,如圖8所示,150 kW/m2工況下該段長度為80 mm,200 kW/m2工況下為60 mm,250 kW/m2工況下為50 mm。這是由于熱邊界層處于發展階段時,發展初期的熱邊界層很薄,近壁區液體溫度較低且與主流區溫度相近,由于溫度場的連續性,壁面溫度較低且與主流區的溫差較小,單相導熱及對流換熱強度較高,隨著壁面對附近流體的加熱,近壁區域熱邊界層增厚,熱阻相應變大,換熱系數下降。熱流密度越大,近壁區域的局部過熱層產生越快,因此,熱邊界層發展所需的通道長度越短。

隨著熱邊界層發展到一定程度,近壁區域的過熱層內部發生沸騰,流場中開始出現明顯的汽泡,沸騰對傳熱的強化作用不斷增強,對流換熱系數由逐漸下降轉變為趨于穩定,進入核沸騰主導段。由于汽泡在各段的生長階段不同,進入核沸騰主導段后對流換熱系數隨位置的變化存在一定小范圍浮動,表明該階段熱邊界層發展對傳熱的抑制減緩,核沸騰對換熱的強化作用增強。

4 結 論

1)短通道內過冷沸騰流場的演變及換熱特性波動受熱邊界層發展和沸騰兩種機制的影響,據此可將短通道加熱區域分為熱邊界層發展段和核沸騰主導段。熱邊界層發展段的前部換熱系數波動幅度較小,原因是入口附近的近壁區溫度較低,受沸騰過程影響較小;熱邊界層發展段后部及核沸騰主導段在壁面附近形成過熱液體層,受沸騰影響較大,換熱系數的波動幅度增大。

2)熱流密度可促進水平管內流動參數和換熱參數沿流動方向的變化。一方面,熱流密度增加,近壁區溫度、平均含氣率及流動速度沿流動方向的提升越快,沸騰越劇烈;另一方面,熱流密度的增加使得對流換熱系數隨熱邊界層發展達到相對穩定所需的距離越短。

綜上,針對高熱流密度工況下的過冷流動沸騰換熱,可以采取適當減小通道長度的方式,以獲得相對更大的對流換熱系數,同時減小沸騰引起的流場參數波動和不穩定性。