隨機過程中的隨機變量概念錯誤及糾正

高宏

［摘 要］文章以維納過程定義為例，分析隨機過程理論在研究單個質點隨機運動時，將質點位移與時間之間的數量關系抽象為隨機變量的基本概念錯誤，以及使用描述大量質點空間位置分布的隨機變量數字特征來刻畫單個質點位移隨時間變化規律的方法錯誤。文章將布朗粒子位移與時間之間的數量關系還原為時間函數，根據愛因斯坦“同一個布朗粒子在不同微小時間間隔中的運動相互獨立”的基本假設，從理論上證明了布朗運動的瞬時速度為白噪聲過程，并基于白噪聲樣本函數重新定義了維納過程，建立了可正確描述單個布朗粒子運動規律的樣本函數模型。

［關鍵詞］隨機過程；隨機變量；樣本函數；維納過程

［中圖分類號］ G644.5 ［文獻標識碼］ A ［文章編號］ 2095-3437（2023）02-0052-05

隨機過程理論是一種利用數學基礎理論和研究方法，探討和揭示客觀世界動態隨機現象數量關系及其變化規律并解決自然科學、工程技術和社會科學等領域實際問題的應用數學理論。隨機過程理論最早源于愛因斯坦1905年對布朗運動的定量研究，隨機過程、隨機變量和樣本函數等數學概念是從質點隨機運動現象中抽象出來的一種數學結構，是人腦對質點隨機運動現象數量關系及空間形式的思維反映。隨機變量基本概念雖然遠離了直觀的經驗世界，卻能更深刻地反映隨機現象的本質。由于隨機變量定義及基本概念的抽象性和復雜性，維納（Wiener）在研究單個布朗粒子所走曲線的數學性質時，將單個布朗粒子的位移與時間之間的數量關系抽象為隨機變量[1-4]，無形中改變了布朗粒子位移函數的定義域和值域，導致研究對象從單個質點改變為質點集合，并用隨機變量的統計特性來描述樣本函數的曲線性質，從而得出了“布朗粒子位移服從正態分布”“布朗粒子位移與時間的平方根成正比”和“布朗運動路徑處處不可導”等一系列與物理學理論和實驗結果嚴重不符的結論，為自然科學、工程技術和社會科學提供了錯誤的理論、方法及工具。

本文擬分析維納過程定義中的基本概念錯誤和研究方法錯誤，基于愛因斯坦“布朗粒子在不同時間間隔中的運動相互獨立”的基本假設，推導出布朗粒子的瞬時速度為白噪聲過程，利用白噪聲樣本函數重新定義維納過程，建立可正確描述單個布朗粒子運動規律的數學模型。

一、概率論中的隨機變量定義

隨機變量是概率論中一個極為重要的基本概念，也是研究隨機現象的基本工具。引入隨機變量的主要目的是把隨機試驗的結果數量化，將隨機事件的結果映射為實數，這樣就可以利用數學分析方法來研究隨機現象。

隨機變量的定義涉及隨機試驗、樣本點和樣本空間三個基本概念。

隨機試驗是指人們對隨機現象進行的觀察或觀測，隨機試驗具有以下三個特征：

（1）可重復性：在相同條件下可重復進行。

（2）多結果性：試驗結果不止一個，但所有可能的結果都是事先明確可知的。

（3）不確定性：每次試驗之前不能確定會出現哪一個結果，但可以肯定會出現所有可能結果中的一個。

盡管一次隨機試驗將要出現的結果是不確定的，但其所有可能結果是明確的。我們把大量重復隨機試驗會出現的每一種可能的結果稱為一個樣本點，一般記為ω；全部樣本點的集合稱為樣本空間，一般記為Ω。

定義：設隨機試驗的樣本空間為Ω={ω}，若X（ω）為定義在樣本空間Ω上的單值實數函數，則稱X（ω）為隨機變量，簡記為X。

隨機變量的取值可以是連續的，也可以是離散的，根據隨機變量取值的不同，可以分為連續型隨機變量和離散型隨機變量。

通常用大寫英文字母X，Y，Z，…來表示隨機變量，用小寫英文字母x，y，z，…表示實數。如果隨機試驗的結果本身就是一個實數x，即樣本點ω本身是一個實數，這時常定義X= X（ω）= ω= x。

對于拋硬幣試驗，試驗結果可能是硬幣正面向上，也可能是硬幣反面向上，即有兩種可能的結果，而且只有這兩種結果，事先可以明確。因此該試驗所對應的樣本空間Ω由ω1和 ω2兩個樣本點構成，我們指定實數1和-1分別與樣本點ω1和 ω2對應（見圖1），則隨機變量可寫成

[X=Xω=? ?1，ω=ω1-1，ω=ω2? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （1）]

從上述隨機變量的定義可以看出，隨機變量X的取值由樣本點ω決定，也就是說，隨機變量X是樣本點ω的函數，即有X= X（ω）。因此，隨機變量的定義域為樣本空間Ω。

隨機變量實質上是一個定義在“隨機試驗所有可能結果集合”上的單值實數函數，隨機變量的不同取值與隨機試驗的所有可能結果一一對應，隨機變量的值隨試驗結果的不同而變化。從數學上講，隨機變量就是一個從隨機試驗結果的集合到實數集的映射。

二、隨機過程與隨機變量的關系

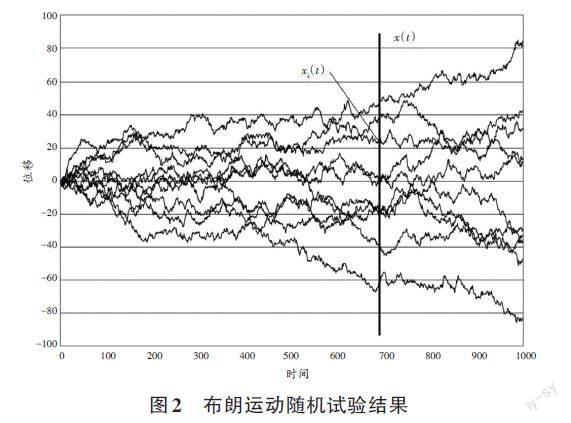
在現實世界中，許多隨機現象都是隨著時間的進程變化發展的，這類動態隨機現象就是所謂的隨機過程。例如在相同條件下重復10次觀察一個從原點出發的布朗粒子位移x隨時間t的變化過程，可得到如圖2所示的10條布朗粒子位移曲線，這10次測量結果也可分別用10個時間函數x1（t），x2（t），…，x10（t）表示。盡管每次的試驗結果各不相同，但每次的結果卻是一個確定性的時間函數xi（t）。若同時觀測10個從原點出發的布朗粒子位移x隨時間t的變化過程，也會得到與圖2類似的試驗結果曲線。

顯然，每個布朗粒子的觀測結果，均為一個隨時間變化的實數，亦即隨機過程的試驗結果是一族時間函數x1（t），x2（t），…，xi（t），…，也就是說，隨機過程試驗的樣本點ωi與時間函數xi（t）一一對應（見圖3）。

由于隨機過程的試驗結果是一族時間函數，因此我們可用定義在Ω×T上的二元函數X（ω，t）來描述隨機過程的所有試驗結果。下面給出X（ω，t）在四種不同情況下的含義：

（1）固定ω，X（ω，t）是一個自變量為t、定義域為T的普通函數，它是一次隨機過程試驗（即在T上進行一次全程觀測）所得到的一條記錄曲線或一個時間函數x（t），通常稱為隨機過程的一次物理實現或一個樣本函數（軌道）。樣本函數x（t）是確定性的時間函數，從時間角度刻畫了隨機過程。

（2）固定t，X（ω，t）是一個定義在樣本空間Ω上的單值實數函數，也就是概率論中的隨機變量，簡記為X（t）。從概率論的觀點來看，隨機過程就是一族有時間標記的隨機變量X（t）。隨機變量X（t）從空間角度刻畫了大量布朗粒子在某一時刻的位置分布規律。

（3）固定ω，固定t，X（ω，t）是一個實數，表示某次隨機過程試驗在t時刻的觀測值。

（4）當ω和t均變化時，隨機過程試驗的所有結果構成一族樣本函數，因此，所有這些樣本函數的總體或集合就構成了隨機過程。

綜上所述，我們可以從兩個不同的角度給出隨機過程的兩種等價定義。

定義1：隨機過程是一族依賴于樣本空間的時間函數集合。

定義2：隨機過程是一族依賴于時間的隨機變量集合。

定義1把隨機過程看成是一族樣本函數的集合，這是概率論隨機變量定義的推廣。概率論將樣本空間中的樣本點映射成實數軸上的一個點，而隨機過程則是將樣本空間中的樣本點映射成一個時間函數（隨時間變化的實數）。

定義2把隨機過程看成是概率論中多維隨機變量的推廣，可以把多維隨機變量的理論作為隨機過程理論的基礎。

以上兩種定義從不同的角度描述了隨機過程，其本質是相同的，互為補充。在工程技術領域對隨機過程做實際觀測常用定義1，觀測次數越多，所得樣本函數數量也越多，則越能掌握隨機過程的統計規律。定義2與概率論中的隨機變量定義相聯系，因此在數學領域做隨機過程理論分析時，常用定義2。時間分割越小，多維隨機變量的維數n就越大，也就越能細致描述隨機過程的統計規律。

在實際應用中，樣本函數x（t）用來記錄或描述一個質點的位移隨時間的變化過程，隨機變量X（t）則用來描述大量質點在某一時刻的空間位置分布。所有質點在t時刻的位置，或所有樣本函數x（t）在t時刻的函數值，就是t時刻隨機變量X（t）的取值。

隨機變量符號X（t）并不表示X（t）是時間t的函數，X（t）是定義在樣本空間Ω上的單值實數函數，它只表示t時刻所有樣本函數的取值，即X（t）={ x1（t），x2（t），…，xi（t），…}。但是在隨機過程理論中，卻出現了用隨機變量X（t）來描述單個質點位移x（t）的基本概念錯誤，無形中改變了樣本函數x（t）的定義域和值域，導致研究對象從單個質點改變為大量質點，從而得出了一系列與事實不符的錯誤結論。

三、各態歷經隨機過程

研究隨機過程的統計特性，從理論上說需要通過實驗觀測得到所有樣本函數x（t），然后才能用統計方法求出不同時刻隨機變量X（t）的數學期望、方差和自相關函數等數字特征，但這在實際研究工作中往往辦不到，因為這需要對一個隨機過程進行大量重復的實驗或觀察，甚至需要實驗次數N趨于無窮大時才能滿足要求。

有一種平穩隨機過程，對其任何一個樣本函數x（t）所做的各種時間平均，從概率意義上趨近于隨機變量X（t）的各種統計平均，則稱之為具有各態歷經性的隨機過程。

各態歷經隨機過程的任何一個樣本函數x（t）都經歷了隨機過程X（ω，t）的所有可能狀態，因此可用任何一個樣本函數x（t）的時間平均來代替X（t）的統計平均或集合平均，簡化隨機現象的測量和計算過程，給解決實際問題帶來極大的方便。

例如，分析電子產品中的白噪聲時，用常規方法，需要在同一條件下，同時測量并記錄所有電子產品中的白噪聲電壓或電流波形，再用統計方法計算出白噪聲過程的均值、方差和自相關函數等數字特征。而利用白噪聲過程的各態歷經性，則只需要在同一條件下，長時間測量并記錄一臺電子產品的白噪聲，然后用求時間平均的方法，即可獲得白噪聲過程的均值、方差和自相關函數等數字特征，大大簡化實際問題的研究過程。

對于隨機游走和布朗運動這類非平穩隨機過程，各個樣本函數具有不同的上升或下降趨勢，整個過程不具有各態歷經性。因此，研究隨機游走和布朗運動的隨機變量和樣本函數時，要分別采用概率分析方法和函數分析方法來研究它們的空間統計特性和時間變化規律。

四、維納過程定義的概念錯誤分析

維納過程是隨機過程理論中一種重要的連續時間隨機過程，是刻畫一系列復雜隨機過程的基本工具。維納過程不僅在隨機過程理論中占有相當重要的地位，而且也是自然科學、工程技術和社會科學研究動態隨機現象的重要數學工具。液體中懸浮微粒的布朗運動、光纖陀螺中的隨機游走誤差和股票市場中的價格波動等隨機現象均可用維納過程進行描述。

（一）愛因斯坦布朗運動理論

布朗運動是物理學中的一個著名現象。愛因斯坦于1905年首先對布朗運動進行了定量研究，為隨機過程理論的建立和發展奠定了基礎。

由于宏觀可觀測物理量與大量微觀粒子運動的統計規律有關，因此愛因斯坦的研究對象并不是一個布朗粒子，而是由大量粒子組成的熱力學系統，愛因斯坦關注的是大量布朗粒子在某一時刻的空間位置分布規律。

愛因斯坦認為布朗粒子的隨機運動是由于受到大量液體分子的高速碰撞而引起的，并提出了“同一個布朗粒子在不同微小時間間隔中的運動相互獨立”和“不同布朗粒子之間的運動相互獨立”兩個假設。

愛因斯坦對一維布朗運動進行了定量研究，假設所有布朗粒子同時從x軸的原點出發，根據熱分子運動擴散方程推導出了大量布朗粒子在t時刻空間位置的概率分布函數

式中D為擴散系數。

顯然，所有布朗粒子在t時刻的空間位置服從數學期望為零、方差為2Dt的正態分布。圖2所示的布朗運動仿真試驗結果也表明，大量布朗粒子在某一時刻的空間位置服從正態分布，其方差與時間成正比。

（二）維納過程定義

維納在研究愛因斯坦布朗運動理論后，發現愛因斯坦僅從統計的角度成功地解釋了大量布朗粒子的擴散現象，但是并沒有給出單個布朗粒子的運動學描述。

維納對單個布朗粒子運動軌跡的數學性質感興趣，首先設X（t）為布朗粒子在t時刻的位移[1-4]，然后根據愛因斯坦的“同一個布朗粒子在不同微小時間間隔中的運動相互獨立”假設和大量布朗粒子在t時刻的位置服從正態分布的結論，給出了如下的維納過程定義：

若一個隨機過程{ X（t），t≥0}滿足

（1）X（t）是獨立增量過程。

（2）X（t）～N（0，σ2t）。

（3）X（t）關于t是連續函數。

則稱X（t）是布朗運動或維納過程。

（三）維納過程定義中的概念錯誤

維納過程首先用X（t）表示一個布朗粒子在t時刻的位移，因此X（t）是定義在時域T上的一般函數，表明X（t）只是隨機過程X（ω，t） 固定ω時的一個樣本函數x（t），映射的是樣本空間Ω中的一個樣本點，亦即布朗運動的一次試驗結果。

維納過程在定義中又假定X（t）為服從正態分布的隨機變量，表明X（t）是定義在樣本空間Ω上的函數，也就是t時刻的隨機變量，映射的是樣本空間Ω上的所有樣本點，亦即布朗運動的所有試驗結果。

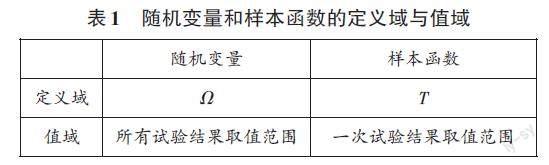
隨機變量和樣本函數是兩個具有完全不同定義域和值域的函數（見表1），描述的是完全不同的隨機現象。維納過程定義使用同一函數符號X（t）來表示樣本函數和隨機變量，從根本上混淆了樣本函數和隨機變量所表達的內涵和外延。

維納過程的研究對象是一個布朗粒子在t時刻的位移X（t），因此X（t）是時間t的一般函數。但是維納過程定義卻將X（t）又當作隨機變量，無形中改變了X（t）的定義域和值域，導致研究對象從單個質點改變為質點集合，加之用愛因斯坦描述大量布朗粒子空間位置正態分布的統計特性來刻畫單個布朗粒子的位移性質，勢必會得出一系列與事實不符的錯誤結論。

五、維納過程性質與事實不符

維納過程將單個布朗粒子在t時刻的位移X（t）當作隨機變量，改變了時間函數X（t）的定義域和值域，從而得出“布朗粒子位移服從正態分布”“布朗粒子位移與時間的平方根成正比”和“布朗運動路徑處處不可導”等一系列與物理學理論和實驗結果嚴重不符的結論。

（一）正態分布假設與經驗事實不符

假設布朗粒子位移X（t）服從（0，σ2t）正態分布，根據正態分布的性質，布朗粒子位移曲線X（t）應具有如下兩個特點：

（1）對稱性：在每一時刻t，絕對值相等的正、負位移出現的次數大致相等。

（2）集中性：在每一時刻t，布朗粒子在0點附近出現的次數最多。

根據維納過程定義X（t）關于t是連續函數的性質，可畫出維納過程描述的布朗粒子位移曲線（見圖4）。

顯然，維納過程描述的布朗粒子位移曲線與圖2所示的布朗粒子位移曲線完全不符。圖2所示的布朗粒子位移曲線均隨時間向遠離原點的方向持續擴散，既不呈現正態分布的對稱性，也不具有正態分布的集中性。

事實上，愛因斯坦關于“布朗運動服從正態分布”的結論指的是大量布朗粒子在某一時刻的空間位置服從正態分布。觀察圖2所示的布朗粒子位移曲線可以發現，所有布朗粒子在同一時刻的位置均服從正態分布，并具有正態分布的對稱性和集中性。

（二）路徑處處不可導性質與物理學實驗不符

維納基于“布朗粒子位移服從正態分布”的假設，還得出了“布朗運動路徑處處不可導（瞬時速度無窮大）”的著名論斷，并認為測量布朗粒子“瞬時速度”的任何努力都是徒勞的。

2010年，美國得克薩斯大學的李統藏成功地利用激光光鑷技術首次實驗測量到了布朗粒子的瞬時速度，實驗結果證明了單個布朗粒子的瞬時速度波形為白噪聲[5]，表明布朗運動的導數（瞬時速度）不僅存在，而且可觀測。

李統藏的研究成果在《科學》雜志上發表后，在全球引起了極大的轟動。《科學》雜志將李統藏的布朗粒子瞬時速度測量實驗推薦為大學及高中教學內容，美國明尼蘇達大學等學校的相關課程已經將該實驗作為教學內容。

六、重新定義維納過程

（一）布朗運動瞬時速度

設x（t）為布朗粒子在t時刻的位移，根據愛因斯坦“同一個布朗粒子在不同微小時間間隔中的運動相互獨立”假設，可知單個布朗粒子的瞬時速度v（t）在不同時刻互不相關，因此v（t）的自相關函數可表示為

[Rvτ=vt-τv（τ）=N0δτ? ? ? ? ? ? ? ? ? ? ? ? （3）]

式中τ為時間間隔，N0為正實常數，δ（τ）為單位沖擊函數。

根據維納-辛欽定理，平穩隨機信號的功率譜密度是其自相關函數的傅立葉變換，v（t）的功率譜密度

[Svf=-∞∞v（t）e-j2πftdt=N0? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（4）]

即單個布朗粒子的瞬時速度v（t）的功率譜密度在整個頻率軸上均勻分布。

式（3）和式（4）表明v（t）為平均功率為N0的白噪聲，與李統藏的布朗粒子瞬時速度測量實驗結果完全相符。

（二）重新定義維納過程

由于單個布朗粒子的瞬時速度v（t）就是單個布朗粒子位移x（t）的導數，白噪聲的平均功率N0等于其方差σ2，因此，可給出如下的維納過程定義：

若n（t）為均值為零、方差為σ2的白噪聲樣本函數，則稱

[xt=0tntdt? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（5）]

為從原點出發的布朗運動或維納過程。

白噪聲是一種理想化的數學模型，由于其自相關函數是一個“沖擊函數”，功率譜密度為“常數”，因此在數學上具有處理簡單、計算方便等優點，在隨機信號分析中占有相當重要的地位。

根據式（5）的單個布朗粒子位移數學模型，可演繹推導出單個布朗粒子在時域及頻域的所有性質和運動規律，以及大量布朗粒子在t時刻服從（0，σ2t）正態分布的結論，與愛因斯坦布朗運動理論完全一致[6]。

七、結論

由于隨機變量定義及概念的抽象性和復雜性，隨機過程理論中出現了將單個質點位移假設為隨機變量的基本概念錯誤。這一基本概念錯誤不僅導致研究對象從單個質點改變為質點集合，而且導致只能使用描述大量質點空間位置分布的統計規律來刻畫單個質點的位移性質，從而得出了一系列與經驗事實不符的錯誤結論，為自然科學、工程技術和社會科學提供了錯誤的理論、方法及工具。“與實際結合，問題驅動”是隨機過程等應用數學學科發展的不竭動力和重要特征，因此，隨機過程理論中關于質點隨機運動的基本概念及研究方法將面臨重大范式變革，新的質點隨機運動理論將替代現有教科書中的內容，把人類對質點隨機運動的認識提高到一個嶄新的水平，為中國的隨機過程學科進入世界一流學科前列提供了千載難逢的歷史性發展機遇。

［ 參 考 文 獻 ］

[1] 卡林，泰勒.隨機過程初級教程[M]. 莊興無，陳宗洵，陳慶華，譯.北京：人民郵電出版社，2007.

[2] 王梓坤.布朗運動的若干結果[J]. 數學通報，1993（6）：35-38.

[3] 錢敏平，龔光魯，陳大岳，等. 應用隨機過程[M].北京：高等教育出版社，2011.

[4] 樊平毅. 隨機過程理論與應用[M]. 北京：清華大學出版社，2005.

[5] LI T C， KHEIFETS S， MEDELLIN D， et al. Measurement of the instantaneous velocity of a brownian particle[J]. Science， 2010，328（5986）：1673-1675.

[6] 高宏. 公理化方法重建布朗運動理論[J]. 數學學習與研究，2020（23）：133-134.

［責任編輯：林志恒］