挖掘意外高效用項集的有效方法
王 斌,姚銀鳳,周 偉,胡克勇
(青島理工大學信息與控制工程學院,山東 青島 266000)
1 引言
頻繁模式挖掘(Frequent Patterns Mining,FPM)[1]作為關聯規則[2]的一種具有代表性的方法,它因能夠有效的找到模式之間的關系而被應用于各種現實問題。然而,傳統的頻繁模式挖掘[3]有一定的局限性。數據庫項目不僅包括頻率,還包括真實世界中的獨特利潤,這意味著頻繁的模式挖掘不能反映現實世界的問題[4]。例如,數據庫中有由鉆石和杯子組成的事務。杯子比鉆石有更高的頻率,但鉆石的利潤高于幾萬個杯子,即鉆石比杯子更有價值。為了克服這一缺點,提出了高效用項集挖掘(High Utility Itemstes Mining,HUIM)[5]。HUIM是一種流行的數據挖掘方法,用于發現客戶事務數據庫中的有用模式。它包括發現產生高效用(高利潤)的項集,即高效用項集(HUIs)。除了客戶交易分析外,HUIM在其它領域也有應用,如點擊流分析和生物醫學[6]等。HUIM可以看作是頻繁項集挖掘問題的擴展,其中單位利潤可以分配給每一個項目。然而傳統的高效用項集挖掘在計算上具有很大的挑戰性,這是由于其缺乏傳統的頻繁項集挖掘中的反單調特性。傳統的HUIM算法還會產生大量的模式,對于用戶來說分析大量的模式是困難和耗時的。此外,隨著發現的模式的增多,HUIM算法的運行時間會變長,消耗的內存也越來越多。因此,高效的HUIM算法需要設計新的數據結構來提高算法性能。近年來提出的HUI-Miner算法[7]采用了效用列表的數據結構,一定程度提高了運行效率,但由于傳統的效用列表占用內存過大,不適用于大型的數據集。最近提出的ULB-miner算法[8]采用了效用列表-緩沖區結構,能夠有效地存儲和檢索效用列表,但隨著大量模式的產生也會導致運行時間長及內存消耗大等問題。因此,有必要尋找一個更小的集合來挖掘高效用項集。
本文提出了一種挖掘意外高效用項集的算法,使用的UHUI-list數據結構能更加緊湊的存儲項集的有效信息,并通過列表的重構及相互結合來進行挖掘工作。本文提出的UHUI-Prune策略能夠有效減少搜索空間,最終尋找到特定子組中所有有意義的高效用項集。最終實驗結果表明該算法性能優于當前先進的算法。
本文第2節介紹了的問題定義;第3節主要介紹了UHUI-list的構造和剪枝策略;第4節介紹了提出的UHUIM算法;第5節在真實數據集上進行實驗并對結果進行分析;第6節進行總結與展望。
2 問題定義
本文目標是在表格式多維數據的事務維度子組中挖掘意外高效用項集。在本節中介紹意外[9]項集(Unexpected Itemsets, UI)及意外高效用項集的相關問題定義。
2.1 意外項集相關概念
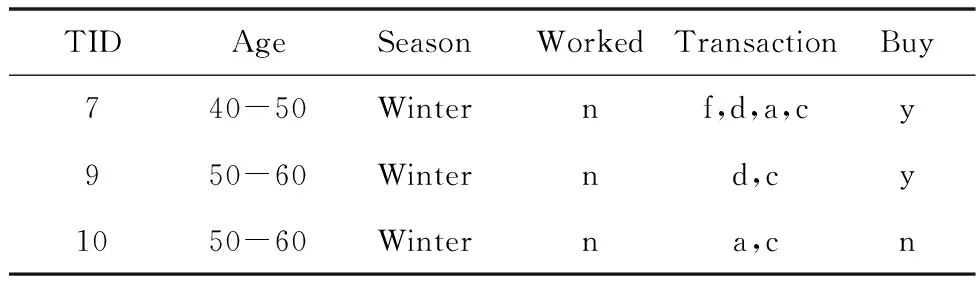
多維表格數據集D由一組元組(也稱為行或事務)組成,其中每個元組t都有一列稱為唯一的元組ID(由TID表示),其它則是稱為屬性的列(由A={a1,a2,…,an}表示)。每個屬性ai都有其值域Rg(ai),見表1。
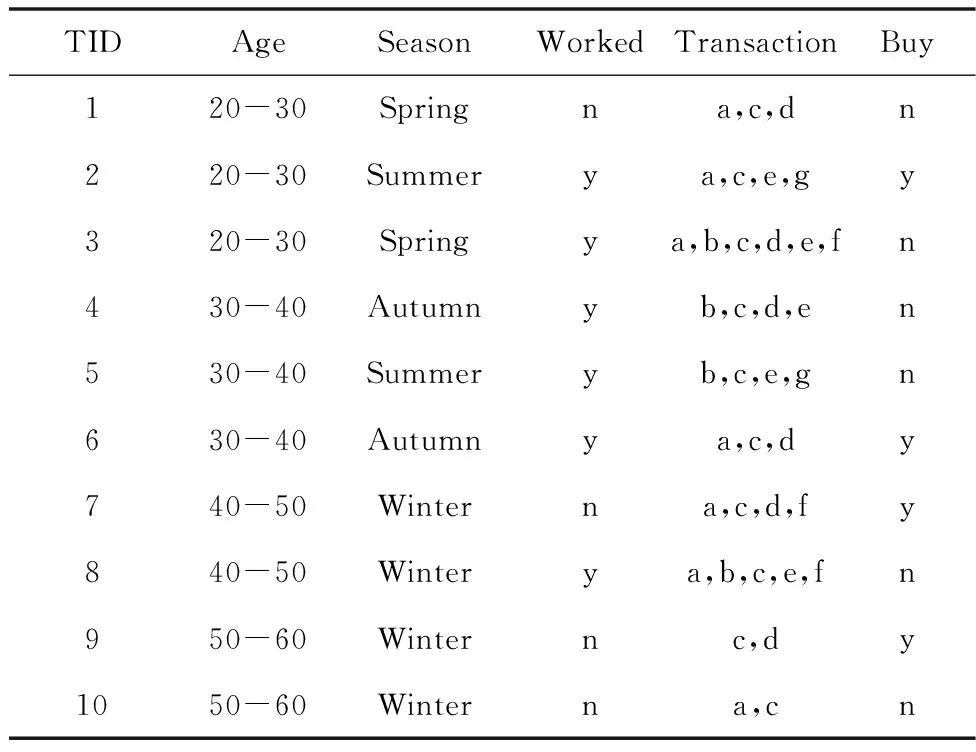
表1 某商品購買實例(其中n=no,y=yes)
D的多維項是一對(ai,vi)對,其中vi是Rg(ai)中可能的值。由Im表示的m級多維項集,它不包含重復屬性。從形式上講,有
Im={(ai1,vi1),…,(aim,vim)}
(1)
D上的多維項集Im的支持度被定義為包含Im的D中元組的百分比。例如,表1中多維項集I0={(season,spring)}的支持度為sup(I0)=0.2。下面需要研究D的切片上多維項集的支持度。給定用戶指定的最小支持度閾值min_sup,如果sup(Im)>min_sup,則多維項集Im在D上是頻繁的。
定義1:D的子組定義為k個多維對的結合,即S(k)={(ai1,vi1),…,(aik,vik)},子組中的屬性值稱為固定屬性值(FVs)。
定義2:給定固定的k個屬性值,通過S(k)中指定的多維對對D執行關系選擇來獲得S(k)的切片[10]。切片中非固定的屬性值稱為可變屬性值(VVs)。
slice(S(k))=σ(S(k))
(2)
例如表1的子組S(1)={(season=winter)}的切片為一個包含TID={7,8,9,10}4個元組的子集,見表2。
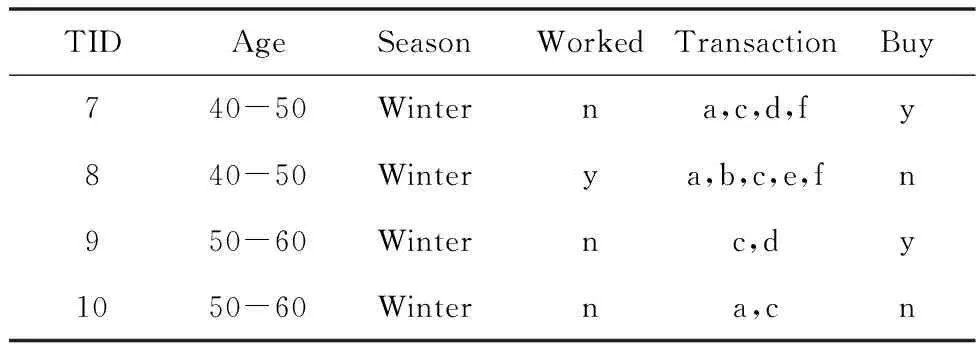
表2 S=(season=winter). winter是一個FV
給定一個子組S(k),在后續對多維項集Im的探索中,不進一步考慮S(k)中的FVs。為簡單起見,將在余文用S表示一個子組。
子組的覆蓋范圍為切片中的元組在整個數據集D中的百分比,表示為
cov(S)=|slice(S)|/|D|
(3)
如果一個子組的覆蓋范圍不小于最小閾值min_cov,則該子組是重要的。如果不存在滿足S?S′的重要的子組S′,則S是最大的重要子組。
定義3:給定min_sup和min_cov,數據集D上的意外項集(UI)被定義為〈子組,多維項集〉對,由
給定min_sup=0.5和min_cov=0.2,很容易看出I1={(buy,y)}在原始數據集D(見表1)上不頻繁,但在子組S1={(season=winter)}的切片(見表2)上頻繁。因此,
通過對D進行切片操作而獲得的子集被稱為參考數據集D′。
定義4:給定一個min_sup,min_cov和D′=R(S),更具體地說,D′=R(S)=slice(S)。一個D′上的意外項集(UI)由
問題1:給定一個多維數據集D,一個用戶指定的子組S,兩個用戶指定的閾值min_sup和min_cov,在對D進行切片操作獲得的D′=R(S)上找到所有意外的項集
在D′=R(S)上,S={(season=winter)}。如果在D′上再執行切片操作,取S={(worked=n)},可得D′的切片,見表3。
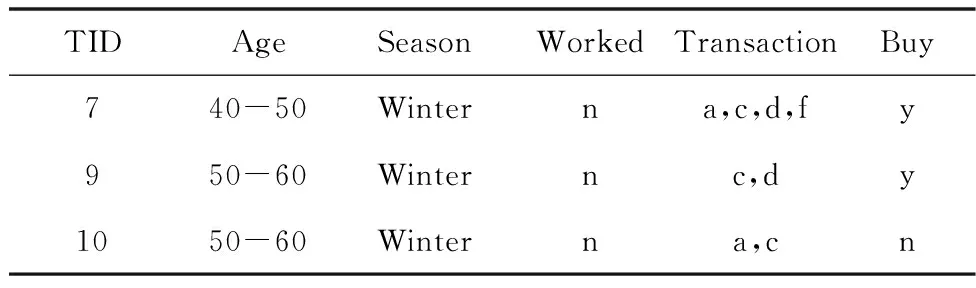
表3 D′=R(S)的切片S={(worked=n)}
2.2 意外高效用項集相關概念
本小節定義了意外高效用項集的相關術語。可見表1 中包含十個事務(Transaction,T),每個事務中包含一系列的項。其中項的頻率是項的內部效用,用IU表示,見表4。項具有獨特的利潤,稱為外部效用[11],用EU表示,見表5。
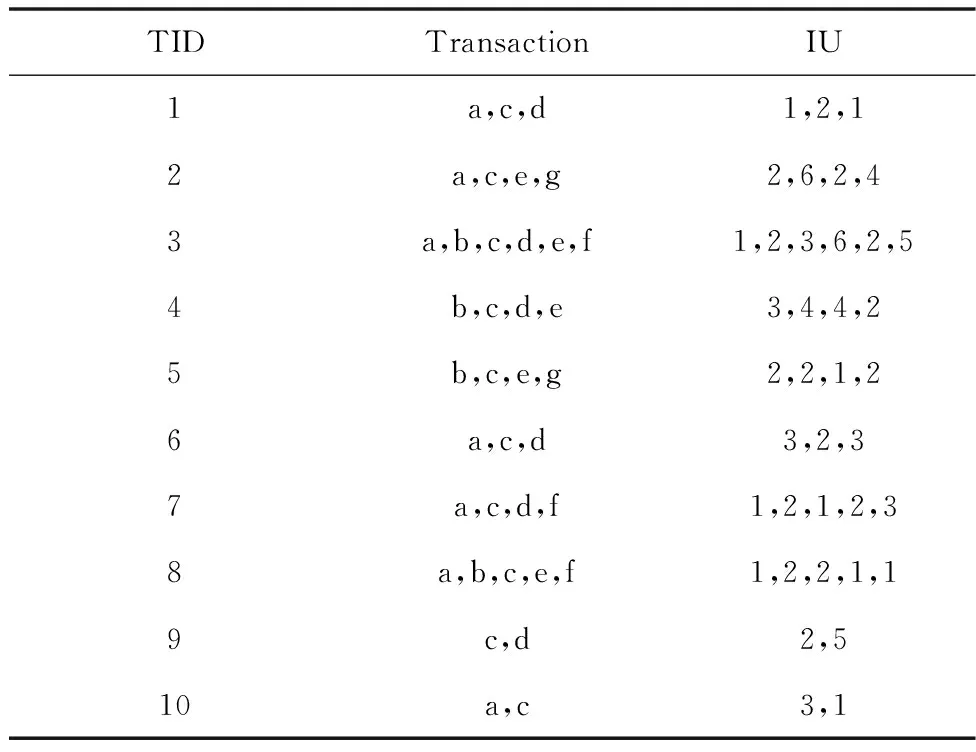
表4 運行數據集D上的事務和項

表5 項的單位利潤表
在D′上,取事務一維進行挖掘,其中I={I1,I2,…,Id}是一組不同的項,事務Tj={xn∣n=1,2,3,…,Nj,xn∈I},其中Nj是事務Tj中項的數量。事務數據庫D有一組事務,D={T1,T2,…,Tj},其中j是數據庫中的事務總數。
定義5:xj∈Tj的效用,表示為U(xj,Tj),計算為事務中項的外部和內部效用的乘積。即
U(xi,Tj)=IU(xi,Tj)*EU(xi)
(4)
定義6:數據庫中的一個子項集X的效用表示為U(X)。U(X,Tj)為項集X在事務Tj中的效用。
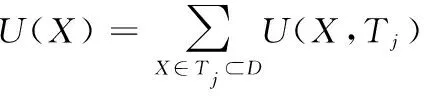
(5)
定義7:事務Tj的事務效用,表示為TU(Tj),定義為
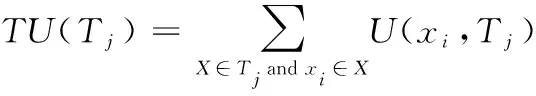
(6)
定義8:項集X的事務加權效用[12]表示為TWU(X),定義為
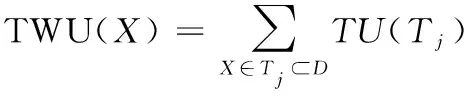
(7)
定義9:最小意外效用閾值表示為uminutil,它的計算方式為數據庫D的總效用和用戶定義的百分比值δ的乘積。
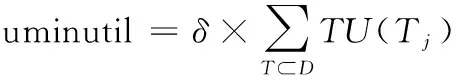
(8)
在本文中,表3僅包含T7,T9,T10三個事務,若給定δ=24%,則uminutil=24%*(16+18+19)=12.72。
問題2:給定一個多維數據集D,一個用戶指定的子組S,三個用戶指定的閾值min_sup,min_cov和uminutil,在D′=R(S)上找到所有意外的項集
定義10:如果項集X的效用大于等于最小意外效用閾值,則X為意外高效用項集,否則舍棄。
U-U(X)≥uminutil
(9)
例如,在表3中,U-U(f)=3<12.72,因此1-項集f不是意外高效用項集。
性質1:對于任意的意外高效用項集X,都存在其超集X′,使得TWU(X′)≤TWU(X)。
證明:設X′為項集X的超集,由先驗屬性[6]知
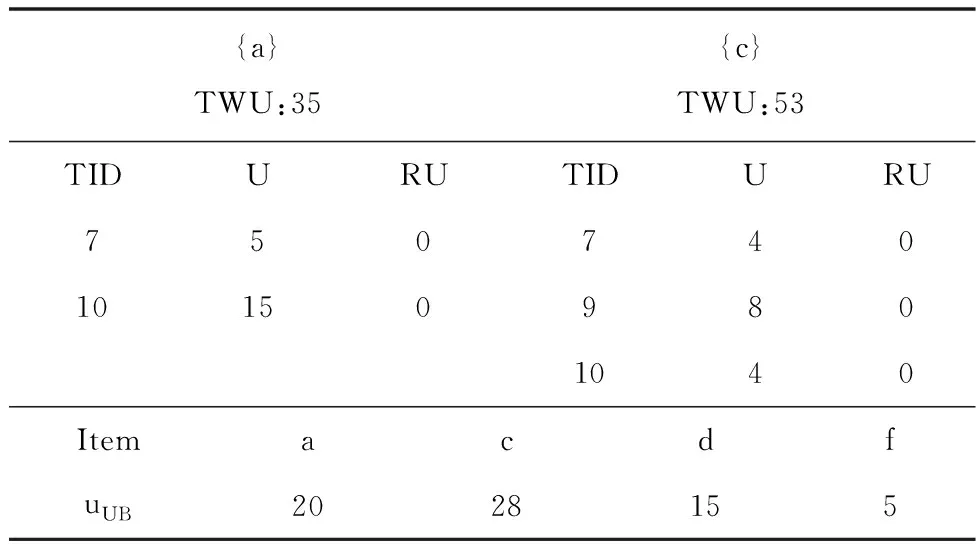
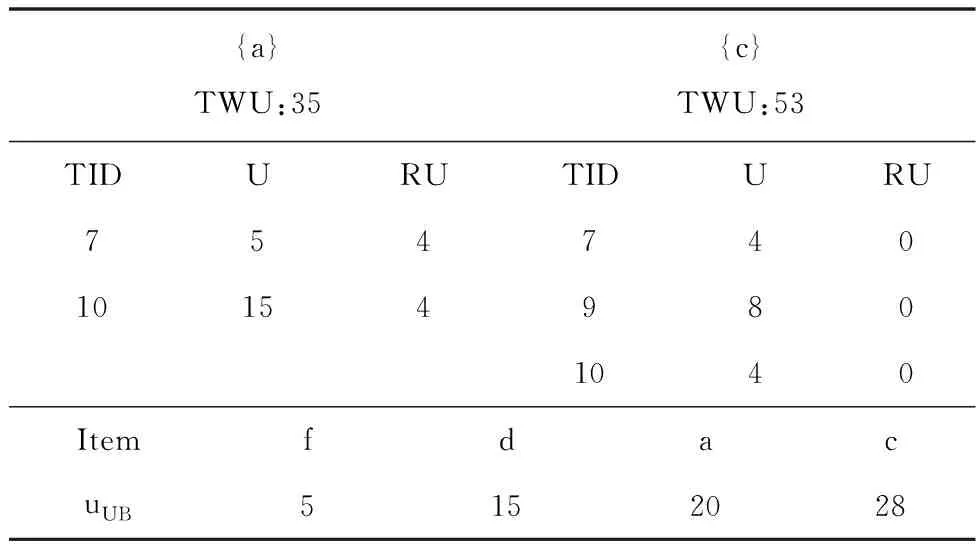
sup(X′) ∵U(X′) 得證。 性質2若項集X不是意外高效用項集,則其超集X′也不會是意外高效用項集。 證明:略。 本節介紹提出的UHUI-list數據結構以及UHUI-Prune策略來更有效地挖掘意外高效用項集。 本文提出了一個新的數據結構UHUI-list來更緊湊的存儲有效的項集信息,該列表包含一系列元組,一個元組包含了該項集所存在的事務的信息。利用UHUI-lists來挖掘意外高效用項集。 3.1.1 相關概念 定義11:在一個事務Tj中,最大效用就是事務T中所包含的項效用的最大值,記為umax(Tj)。 umax(Tj)=max({u(xi,Tj)|xi∈Tj}) (10) 定義12:對于項集X,包含X的所有事務的最大效用之和稱為效用上限[13],記為uUB(X)。 (11) 定義13:事務Tj中項集X的剩余效用[14]記為RU(X,Tj)。 (12) 其中Tj/X表示為在事務Tj中位于項集X后的所有項的集合。例如,在表3中,RU(ad,T7)=3。 數據庫D中項集X的剩余效用記為:RU(X)。 (13) 3.1.2 UHUI-list構造過程 項集X的UHUI-list記為UL(X),由UL(X).TWU和n個UL(X).tuplen兩部分組成。UL(X).tuplen由以下三部分組成:事務標識符TID;項效用U,表示為UL(X).tuplen.u;剩余效用RU,表示為UL(X).tuplen.ru。UHUI-list的創建過程如下: 1)掃描D′的切片S={(worked=n)}并讀取第一個事務T7。由表3可知,T7={a,c,d,f},從a項開始創建UL(a)。RU值初始化為0。將UL(a).tupleT7附加到UL(a),UL(a).tupleT7可表示為<7,5,0>。然后以同樣的過程創建UL(c)等; 2)按照上述過程依次對T9,T10創建UHUI-list,直至所有事務的所有項構建完,見表6。 表6 構建UL(a)、UL(c)和uUB表 3)對所有的事務中的各項創建完UHUI-list之后,由定義8可得a、c、d、f的TWU值,由定義12可得uUB表。見表6。 3.1.3 UHUI-list重構 UHUI-list創建完成后,重構過程如下: 1)對上述創建UHUI-list的所有項按照uUB升序排序,結果為:f?d?a?c,根據uUB升序對表3重新進行排序,見表7。 表7 按uUB升序排序后的S={(worked=n)} 2)由f?d?a?c的最后一項c開始重構UHUI-list,由表7可重新計算RU值。在此過程中,各項的TWU值不變。RU值計算完成后,重構過程結束,見表8。 表8 重構的UL(a)、UL(c)和uUB表 當前的UHUI-lists包含按照uUB升序排序的1-項集,挖掘過程從含有最小uUB值的UHUI-list開始。 3.2.1UHUI-Prune策略 本文提出UHUI-Prune策略,即在用戶定義固定屬性值下得到的意外高效用項集的數據集DU上進行剪枝,該策略主要分四步進行剪枝: 剪枝1(U-TWU剪枝)在數據集DU上,若TWU(X) 剪枝2(U-uUB剪枝)在數據集DU上,若uUB(X) 剪枝3(U-EUCS′剪枝)在數據集DU上,若EUCS(X) 剪枝4(U-U剪枝)在數據集DU上,若RU(X)+U(X) 由UHUIs定義以及上述剪枝可知d,f兩項不是UHUIs,由于d,f不滿足U-TWU剪枝,故其擴展項有可能為UHUIs,但f項滿足U-uUB剪枝,故剪枝掉f項。 3.2.2 從UHUI-lists中挖掘UHUIs 下面介紹UL(Xi)相互結合的過程步驟:假設重構后的項集排序為:X1?X2?X3?…?Xi。 1)檢查X1是否為意外高效用項集,如果U(Xi)≥uminutil,則Xi為意外高效用項集; 2)檢查X1的超集是否為意外高效用項集:若TWU(X1)≥uminutil,則X1的超集可能為意外高效用項集。經U-TWU剪枝策略過濾后,將剩下的項進行U-uUB剪枝,若uUB(X1)≥uminutil,則繼續對X1進行挖掘; 3)對X1進行列表結合。首先與下一項X2進行結合產生X1X2,具體結合過程如下:先將UL(X1)與UL(X2)中具有相同TID的元組進行結合。假設X1和X2出現在同一個事務Tm中,則生成一組列表UL(X1X2).tupleTm;其次UL(X1X2).tupleTm.u的計算分為兩種情況: 第一種,如果X1X2沒有共同前綴,則 UL(X1X2).tupleTm.u =UL(X1).tupleTm.u+UL(X2).tupleTm.u (14) 第二種,如果X1X2有共同前綴X0,則 UL(X1X2).tupleTm.u=UL(X1).tupleTm.u +UL(X2).tupleTm.u-UL(X0).tupleTm.u (15) 接下來UL(X1X2).tupleTm.ru的計算如下 (16) 并對于X1X2的每個元組都執行上述過程;最后計算UL(X1X2).TWU:X1X2的TWU值為其所在共同事務中的事務效用之和; 4)在將兩個UHUI-lists的元組組合起來后,下面將計算X1X2是否可擴展挖掘:先計算U-U(X1X2),如果U-U(X1X2)≥uminutil則X1X2為意外高效用項集;其次若EUCS(X1X2)≥uminutil,則X1X2的超集可能為意外高效用項集。 從X1到Xi重復上述所有過程以進行UHUI-lists的結合。如果生成具有前綴X1組合的UHUI-lists,則對這些組合的UHUI-lists執行挖掘過程,運用剪枝4:U-U剪枝。這個過程將遞歸地重復,直到基于最后一個項集的組合過程結束。最終挖掘結果為:g0gggggg,{dc},{dac},{a},{ac}和{c}為意外高效用項集。部分結果見表9。 表9 UL(dc)及UL(dac) 本節介紹UHUIM算法的偽代碼。對于D的任何給定的切片,用(S,I)all表示切片S上所有意外項集的集合。 Algorithm 1(UHUIMmainalgorithm) 1)K=1 2)生成候選的1-Mitemsets集合I-1 3)基于I1生成重要的1-subgroups集合S1 4)Repeat 5)Sk+1=? 6)for all significant k-subgroup S∈Skdo 8)Sk+1. add All(Snew) 9) K=k+1 10)untilSk=? 11)kmax=k-1 12)for k=kmax-1 to1 do 13) for allsignificant k-subgroupS∈Skdo 15)?I ∈(S,I)all,return (S,I) as 意外項集 16)將(S,I)存入集合(S,I)all中 ∥(S,I)all用于保存所有的意外項集 17)Generate_UHUIs((S,I)all,uminutil);∥生成意外高效用項集 18)End Algorithm 2 (Generate_UHUIS) Input:所有的意外項集(S,I)all 用戶指定的最小效用閾值uminutil Output:A list of unexpected high utility itemsets A set of UHUI-lists of 1-length itemsets,UHUI-lists 2)A set of unexpected high utility itemsets,Result-Set 3)A table of upper bound of 1-length itemsets, uUB 4)Foreach 意外項集(S,I) ∈(S,I)all 5)For each 事務Transaction∈(S,I) 6)Foreach i in Transaction 7)If i not in UHUI-lists 8) insert i into UHUI-lists 9) Else 10) Update entry of I in UHUI-lists ∥更新UHUI-list 11) Calculate umaxof T and update uUB 12)Restructure(UHUI-lists, uUB)∥重構UHUI-lists 13) If user requests mining ∥如果用戶請求挖掘 14)Mining(NULL,UHUI-lists,uminutil,Result-Set)∥執行挖掘操作 15) Return Result-Set∥返回意外高效用項集 在本節中,評估了該挖掘方法的性能。為了客觀地比較方法,UHUIM算法與當前最先進的兩個算法ULB-Miner以及HUI-Miner進行對比評估。 所有的算法都是由Java編程語言實現的。PC環境包括32GB內存、4.00GHzCPU和Window10(64位)操作系統。本文在3個真實數據集上評估三個算法的運行時間、內存使用及可伸擴展性性能。所有數據集均可從SPMF庫[15]下載。數據集特征見表10。 表10 數據集特征 本節比較了UHUIM,ULB-Miner及HUI-Miner三種算法在3個真實數據集上的運行時間性能。對于小型稠密的數據集chess,當uminutil為3500000左右時,UHUIM算法比ULB-miner算法的運行時間快一個左右數量級,當uminutil越小,運行時間越長。實驗結果表明,3種算法的運行速度由快到慢為:UHUIM>ULB-Miner>HUI-Miner。見圖1(a)-(c)。 圖1 在不同uminutil值下的運行時間性能 本小節對三種算法進行內存性能評估。大中型數據集chainstore及connect高于chess的內存使用。對于chainstore,在uminutil=1000000時,ULB-Miner算法比UHUIM算法的內存使用多大約5倍,HUI-Miner算法使用內存約為UHUIM算法的3.7倍。實驗結果表明,UHUIM算法的內存消耗低于其它兩種算法。見圖2(d)-(f )。 圖2 在不同uminutil值下的內存使用性能 由圖1、2可知,UHUIM算法在大小不同的3個數據集上運行時間差別不大,內存性能也高于其它兩個算法。因此,UHUIM算法在各個數據集上的可伸縮性均優于ULB-Miner算法及HUI-Miner算法。 本文提出的UHUIM算法能夠有效的挖掘意外高效用項集,給經營者帶來意想不到的利潤。本文采用新提出的UHUI-list結構更緊湊的存儲項集信息,節省時間與空間。本文提出的UHUI-Prune策略能夠有效的減少搜索空間,提高挖掘效率。經過在3個真實數據集上進行運行時間、存儲空間及可伸縮性的實驗評估,結果表明本文提出的UHUIM算法性能優于ULB-Miner算法及HUI-Miner算法。 在未來的工作中計劃調整UHUI-list為UHUI-list-緩沖區結構,并研究在動態數據庫中挖掘意外高效用項集的有效方法。3 基于UHUI-lists的UHUIs挖掘
3.1 UHUI-list的組成及構造

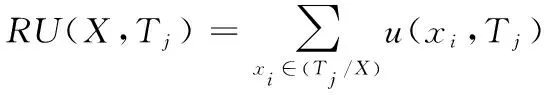
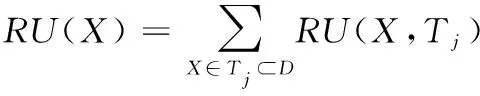
3.2 剪枝策略及挖掘過程
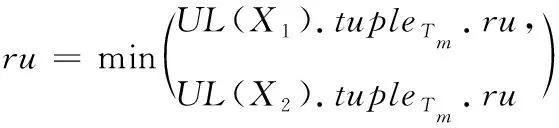

4 UHUIM算法
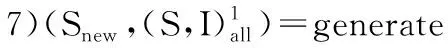
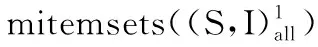
5 實驗
5.1 實驗設置
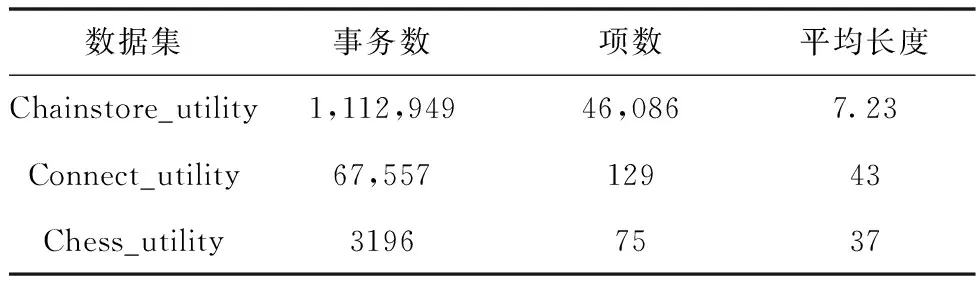
5.2 對運行時間性能的評估
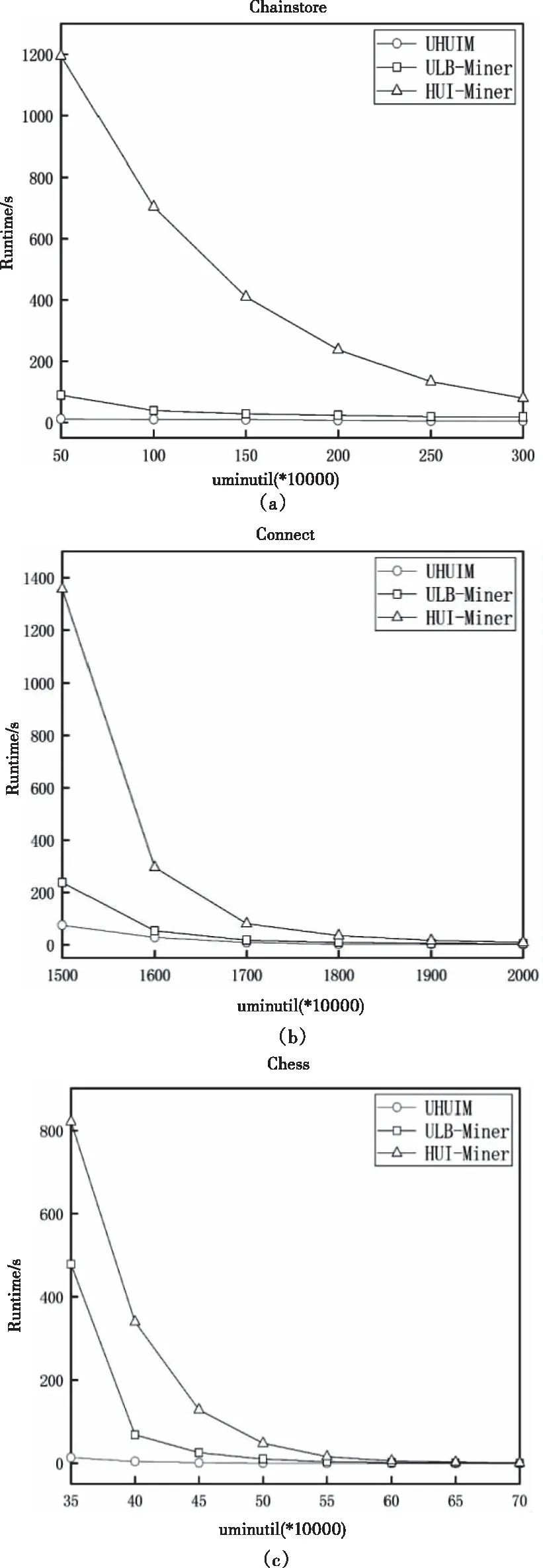
5.3 對內存使用性能的評估
5.4 對可伸縮性的評估
6 結束語

