網絡集群部署數學建模設計與仿真

徐成桂,徐廣順

(成都理工大學工程技術學院,四川 樂山 614000)

1 引言

網絡用戶數量持續增多背景下,對網絡的建設提出更嚴格的要求。用戶的高并發訪問會導致服務訪問速率較慢[1]、服務可用性降低,任何系統故障均會對用戶造成重大損失。集群為使用一組獨立服務器構成的節點集合,為用戶提供統一的服務器資源,完成資源共享的同時實現網絡的負載均衡[2]。傳統的集群部署形式多數采用磁盤共享掛載、共享儲存的策略,現已無法滿足當前網絡服務需求。為滿足用戶大規模的訪問量,完成數量龐大的任務請求[3],服務器要具備較高的儲存空間與并發承受能力,并安置多個網絡集群,通過多個服務節點分擔網絡負載,完成網絡系統高可靠性的運行任務。

針對網絡資源分配及部署問題,文獻[4]通過開放Jackson排隊網絡建模業務流時延,融合遺傳算法與模擬退火算法映射服務節點,使用個體約束性評估防止出現局部最優。文獻[5]考慮時延、能耗、等元素對服務器選擇的影響,基于參數的線性加權排序候選服務器,挑選最佳移動邊緣計算服務器為用戶提供服務。

以上方法的參數選擇均具有一定主觀性,導致其集群部署存在不同程度的偏差。為此,提出基于約束最大熵的網絡集群部署數學模型。分析物理主機屬性,計算并發用戶個數、最高在線用戶數等指標完成作業資源統計;使用約束最大熵法判斷各類參數及指標的重要性,通過圖分割理論實現網絡集群部署模型構建目標。仿真驗證了所提模型的實用性與應用優勢。

2 網絡集群作業資源統計

網絡集群部署前,首先要明確現階段用戶數據訪問行為對網絡資源的實際需求。把物理主機目前的屬性狀態記作

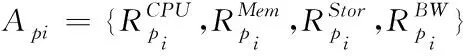
(1)

集群部署物理主機時,要掌握主機能夠供應的資源上限[6],對比集群資源需求和物理主機能提供的資源。物理主機資源即為物理主機減去目前負載后的剩余資源,將式(1)內的屬性參數拓展為

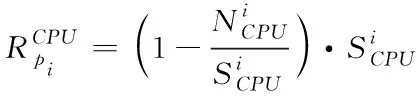
(2)

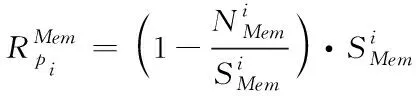
(3)

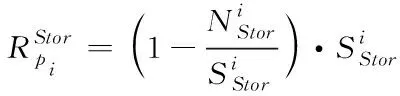
(4)

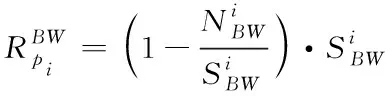
(5)

以并發用戶個數為基礎[7],將最高在線用戶數表示為

U=AU×UP

(6)

其中,AU表示網絡用戶總數,UP為并發比率。

服務器文件儲存容量計算過程為

SC=AU×DC×YD×F/(1-O)

(7)

其中,DC為各用戶每日生成的信息增量,YD為有效工作時間,O為儲存冗余量比率,F表示網絡集群系統未來業務量發展的冗余空間。

將xe(k)的關聯系數描述成

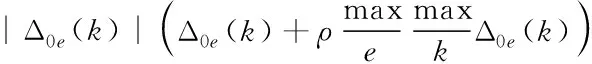
(8)

其中,ρ表示分辨指數,其數值越小,表明分辨能力越好,一般取值為0.6。

最終將關聯度ri解析式設置成

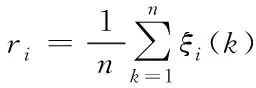
(9)

其中,n表示服務器數據集總數,ξ為關聯系數。

通過上述過程,即可按照不同的用戶訪問行為劃分集群作業類別與數據規律,完成作業資源需求量評估任務,為服務器集群部署策略的實時性調整發揮關鍵作用。

3 基于約束最大熵的網絡集群部署數學建模

3.1 約束最大熵下集群部署參數重要性估計

網絡集群部署操作中包含諸多參數,例如磁盤、網絡利用率、內存等。使用約束最大熵算法推導部署參數的重要性,挑選最關鍵的集群部署計算參數進行數據分析,降低計算量的同時,保證集群部署模型性能可靠性。

最大熵基礎定理為在滿足全部已知時間的前提下,客觀判斷未來事件[9]。采用約束最大熵進行集群部署參數估計主要考慮以下幾點:約束最大熵方法中使用的分布參數對數據的先驗分布沒有嚴格要求,能夠隨意搭配,且不會降低參數重要性估計正確性與一致性。與此同時,該方法能有效處理參數評估中的平滑問題,適用于不同應用環境下的高精度參數重要性評估任務。

在符合復雜度約束條件的概率分布集合A中,挑選具備最大熵H(p)的模型p*,記作

(10)

式中,x、y均為隨機變量相對的網絡服務任務,p(y|x)為條件分布值。

信息論領域中,使用對數評價函數[10]來分析兩個參數在相同空間內的概率分布差別,此種評價函數即為Kullback-Leibler(KL)距離[11]。假設a為問題域U內的一個概率密度函數,a′為概率密度函數a的近似函數,將二者之間的KL距離表示為

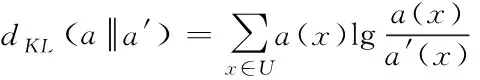
(11)

使用KL距離描述集群部署參數重要性估計的準確率,計算公式為

(12)

3.2 網絡集群部署模型實現

數據通信網絡通常為三層結構體系[12],從上至下分別為核心交換機、聚集交換機與接入交換機。使用約束最大熵算法完成集成參數計算后,以輸出的參數結果為前提,形式化定義虛擬環境下服務器之間的通信代價。集群部署點通信代價為隨機兩個部署點路由經過的最小交換機數量,設置相同物理主機內的虛擬機通信代價為0。

針對架構各異的數據通信網絡,其部署代價矩陣也各不相等。以樹結構為例[13],將其網絡通信代價矩陣定義成

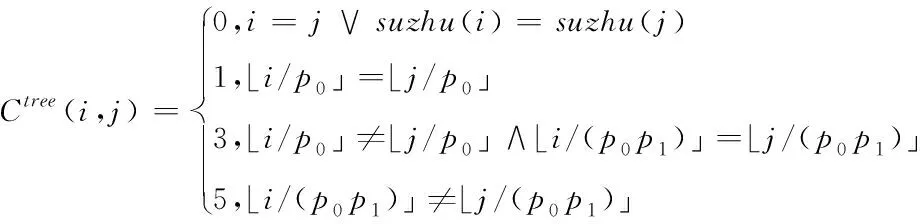
(13)

式中,p0代表接入交換機端口數量,p1為聚集交換機端口數量,i、j均為部署點編碼,suzhu(i)為部署點i所處的宿主物理服務器。

假設D(i,j)為服務器邏輯架構內的通信代價矩陣,通信代價為網絡數據傳輸速度[14]。此種狀態下,將服務器集群部署問題描述為

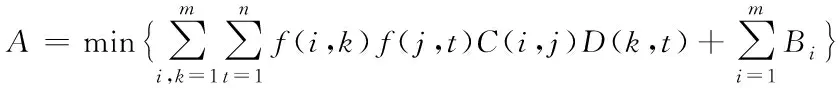
(14)

其中,C(i,j)代表部署點i、j之間的代價,m為部署點數量,Bi為服務器i最高服務帶寬。

服務器集群可劃分成三種計算方法:批處理計算、內存計算和圖計算。其中,圖論為數學領域的關鍵分支,圖割論為一種在圖論基礎上,被廣泛應用的圖像處理方法。服務器集群的結構形態和圖論中的圖像有一定相似性,使用圖割論的有關知識完成網絡集群部署模型構建。將圖論中的圖表示成

G=(V(G),E(G))

(15)

式中,V(G)代表圖G全部頂點的總和,即圖的頂點均為V(G)內的元素;E(G)為圖G全部邊的總和,G內的元素為不同點之間的連線。

集群部署前要充分考慮其資源利用率,以免造成資源浪費。按照集群資源需求量推導出服務器集群部署后,各類資源的資源利用率為否超出當前物理主機的負載量,將資源利用率計算公式表示為

(16)

網絡集群包含多個服務器,與單服務器相比,其資源需求較高,接下來,構建以圖分割[15]為原則的網絡集群部署數學模型。設定初始網絡服務器集群相對應的圖為C,其頂點集合為V(C)={AVM1,AVM2,…,AVMn},邊集為e={AVMi,AVMj},將圖C劃分成o個子圖,記作C1,C2,…,Co,o個子圖相對的子圖密度為D1,D2,…,Do,子圖內的頂點數量為h,將網絡集群部署模型定義成

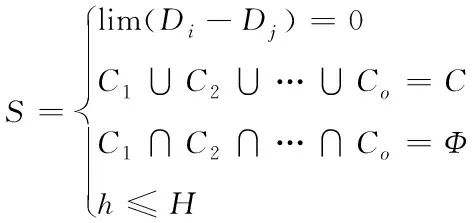
(17)

其中,Φ表示一個空集,H為子圖頂點數量的臨界值。

4 仿真研究

為分析所建網絡集群部署模型的可靠性,設計仿真。仿真軟件為MATLAB 2020b,在計算機上搭建20個節點的物理集群,各物理節點上運行Docker 7.1容器引擎來創造虛擬節點,最多同時運行3個虛擬容器,虛擬容器的最高規模為42個節點。集群負載可以展現集群部署的信息處理能力,將其作為衡量網絡集群部署優劣的指標,驗證本文方法能否依照負載變化情況及時調節集群形態,明確方法的靈活性與有效性。構建兩種負載數據集:第一種按照靜態部署節點比例設置作業類型,記作N1;第二種不依照節點比例設定作業類型,記作N2。實驗的仿真時間為55min。

圖1為本文方法在兩種不同負載運行狀態下,服務器節點狀態改變次數和相應的計算時長。第一種負載數據集下,服務器節點狀態僅出現4次改變;第二種負載數據集下,服務器節點改變次數明顯增多。這為因為N1負載數據集為憑借原始服務器節點比例設置的,網絡集群模型無需調整計算形態就能很好地實現集群部署任務,因負載噪聲引發了4次節點調整策略,處于模型計算誤差可容納范圍;因為N2數據集改變了原有的節點比例,所以產生了大量節點調節現象。

圖1 不同負載數據下本文方法服務器節點調節情況

由圖1可以看出,本文方法能夠按照實際網絡應用情況計算負載變化,并通過節點的實時調節更改網絡集群部署形態,為用戶提供貼合自身需求的網絡服務,具備較強的實用性。

為進一步展現本文方法可用性,將其與文獻[4]遺傳模擬退火法、文獻[5]多重指標法進行仿真對比。定義每個部署任務對CPU的需求大小為2100×24×60×60MI,數據中心具備150臺物理主機與300臺虛擬機,依次使用三種方法把服務器部署于物理主機上,考察三種指標:集群部署時間、物理機應用個數和CPU利用率。圖2為三種方法網絡集群部署的響應時間均值對比結果。

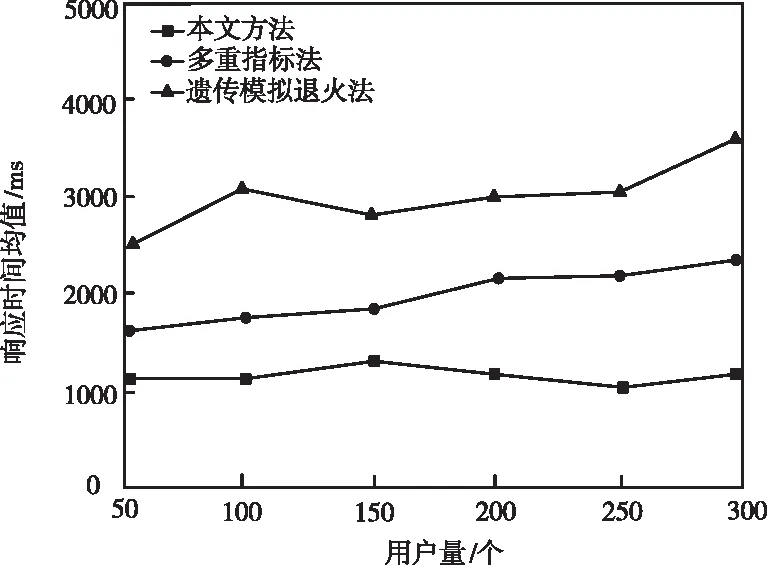
圖2 三種方法集群部署響應時間均值比較

由圖2可知,與兩種文獻方法相比,本文方法部署響應時間最短,且不會伴隨用戶數量的激增產生較大波動,穩定性強。出現此種現象的原因在于,本文方法采用約束最大熵方法,在眾多部署參數中挑選重要度靠前的參數,有效降低計算量,大幅縮短部署響應耗時。

隨機抽取60臺物理主機與60臺服務器進行相同的資源任務,依次使用三種方法進行集群部署,研究不同方法使用的物理主機個數,結果如圖3所示。

圖3 三種方法物理主機應用個數對比

從圖3看出,三種方法集群部署使用的物理主機個數均具備相同趨勢,但本文方法物理主機應用數量最少。這為由于本文方法把資源需求相近的服務器進行集群再完成部署,降低了物理主機個數。遺傳模擬退火法即便考慮了物理主機的負載均衡因素,但其部署效果依舊不如本文方法;多重指標法采用一臺服務器部署在一臺物理機的策略,耗費大量主機資源。

將15分鐘劃分為一個單元,計算75分鐘,即5個時間單元下三種方法執行服務任務時,物理主機的CPU利用率情況,仿真結果參考圖4。

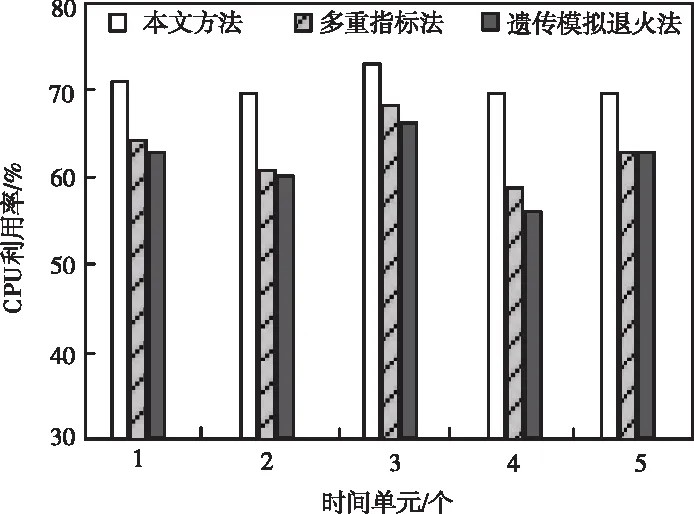
圖4 三種方法CPU利用率對比

觀察圖4可以看到,由于兩種文獻方法的物理主機資源充足但服務器需求較少,極易產生資源利用率低的現象,本文方法的CPU利用率要明顯高于兩種對比方法,證明本文方法在相同的集群部署時間內能執行更多的應用程序,給用戶提供更豐富的資源服務。

5 結論

為實現高質量網絡集群部署,為用戶提供優質的網絡應用服務,提出一種基于約束最大熵的網絡集群部署數學模型。所提方法具有理想的可應用性,適用于高并發的用戶訪問高峰期,與傳統集群部署模型相比,運行成本較少,避免了資源浪費。但是,本文方法是建立在網絡結構已知的情況下,面對結構未知網絡時如何快速有效地實現精準部署,將在今后研究中加以深入探究。