倉庫揀貨員多任務路徑優化

楊東起,駱心怡,毛 鵬?

(1. 南京林業大學輕工與食品學院, 江蘇 南京 210037;2. 南京林業大學土木工程學院, 江蘇 南京 210037)

1 引言

隨著大數據、智慧供應鏈的興起和科學技術的快速發展,眾多企業的商務模式與供應鏈運營相互作用,產生了新業態[1]。為了提升企業核心競爭力,以期能更好地調控供應鏈運營中的費用,倉庫的成本管理十分非常重要[2]。越來越多的企業為了使倉庫施行更有效的庫存信息化管理和提高貨物的搬運效率,紛紛建立智能倉庫進行倉儲管理[3]。倉庫的取貨最優路徑是使倉庫管理高效運行的核心[4],因此,為了使倉庫的管理更加智能化,提高揀貨員的工作效率,眾多學者進行了倉庫取貨的路徑規劃研究。

路徑規劃的算法主要有傳統算法、智能優化算法[5]。現大多數學者在原先的算法上進行改進,引入模型得出路徑調度的進一步優化。如Xing等人[6]對禁忌搜索(NTS)算法進行改進,在鄰域搜索過程中設計了重定位和交換操作,優化了取貨點的順序,從而提高了揀貨的工作效率。傳統的A星算法存在計算量大的缺點[7],為此,Zhang等人[8]先基于A星算法得到初始路徑,采用關鍵點選擇策略進行二次規劃,以去除路徑中冗余的拐點和節點,提供更有效的倉庫路徑規劃。上述的兩種算法均屬于傳統的路徑規劃算法,智能優化算法中,由于遺傳算法具有較好的魯棒性和并行性,能夠獲得滿足特定要求的最優解,被廣泛應用于倉庫的路徑規劃中[9],改進遺傳算法以解決倉庫的路徑規劃問題受到了大量學者的關注。如Zhu等人[10]提出了一種平均分布遺傳算法,預先調整隨機輸入的染色體,以生成更合理的染色體,使迭代過程可以更高效地進行,同時避免早熟收斂,有效地處理了揀貨調度問題。Paraskevi等人[11]將遺傳算法與倉庫揀貨的距離和容量的模糊模型相結合,給出了不同情況下的路徑調度最優解。Liu等人[12]將兩種自適應遺傳算法和一種多自適應遺傳算法相結合,優化揀貨的任務調度,具有較強的全局搜索能力和較快的優化速度。

然而上述文獻均只考慮了揀貨員執行一個任務時的路徑優化,在實際生活中,由于揀貨員數量有限,他們常常需要連續執行多個任務。此外,上述文獻中提及的倉庫規模較小,當倉庫規模較大時,現有的方法難以滿足需求。

針對上述問題,本文將揀貨員的多任務拆分為若干個單任務,依次利用改進的遺傳算法求解其最短路徑。為了解決因大量計算兩點間的距離而導致求解過程耗時的問題,本文創新性的總結了揀貨員從當前位置運動到下一位置的路程計算公式,并引入了距離查找表。

2 問題描述

本文的倉庫模型由貨架和復核臺組成,其規模較大。貨架共4排,每排25組,每組2列,每列貨架包含15個貨格。貨格共3000個。復核臺共13個,位于貨架外圍,成直角分布于倉庫左下角,縱5橫8。任意兩組水平方向相鄰的貨架之間的距離為1500mm,任意兩組豎直方向相鄰的貨架之間的距離為2000mm。貨格長寬均為800mm,復核臺長寬均為1000mm。除貨架和復核臺,倉庫其它地方皆可通行。圖1為倉庫的局部(倉庫的左下角),包含1排7組,其每組2列,每列貨架包含15個貨格。

圖1 倉庫局部示意圖

在揀貨過程中,揀貨員執行單任務的路徑是由起始復核臺、若干貨格和終止復核臺構成,可表示為

T={Sstart,L1,…,Li,…,Ln,Send}

(1)

其中,Sstart表示起始復核臺,Send表示終止復核臺,Li表示第i個貨格。

實際生活中,一個揀貨員會接到多個任務,揀貨員每完成一個任務時,必須到復核臺核對。此時,揀貨員接到的多任務表示為

P={T1,…,Tj,Tj+1,…,Tm}

(2)

其中,Tj為揀貨員的第j個單任務。Tj+1的起始復核臺為Tj的終止復核臺。

3 貨格/復核臺間距離計算

揀貨員從當前位置(xi,yi)運動到下一位置(xi+1,yi+1)時,如果其中的某段路程同時滿足:(1)連續兩次轉向,且方向相同(同為順時針或者逆時針轉向);(2)包含當前位置(xi,yi)或者下一位置(xi+1,yi+1),那么稱它為“N”型路程,如圖2中的路線ABCD。揀貨員運動時通過偏移量才能繞過貨架或復核臺。圖2中,線段AB、CD、EF和GH為橫向偏移量,CI和FJ為縱向偏移量。所有的偏移量均記為bias=750mm。

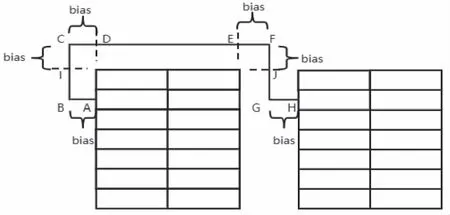
圖2 兩貨格間的路徑示意圖

當計算揀貨員從當前位置(xi,yi)運動到下一位置(xi+1,yi+1)的路程時,如果揀貨員無需繞過貨架,如圖3所示,那么當前位置和下一位置滿足以下條件之一:

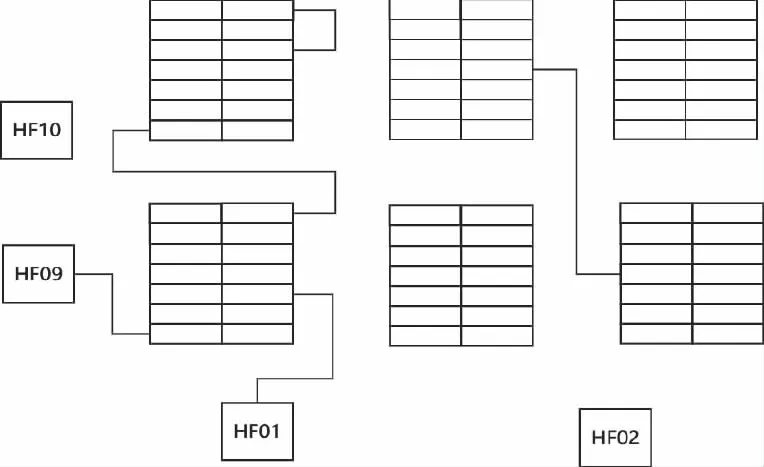
圖3 揀貨員從當前位置運動到下一位置的路徑示意圖

1)當前位置和下一位置分布在同一過道的一側或兩側

2)當前位置和下一位置不在同一排貨架。

此時,揀貨員的路程可表示為:

D(i,i+1)=|xi-xi+1|+|yi-yi+1|+2n×bias

(3)

其中,n為“N”型路程的個數。

當計算揀貨員從當前位置(xi,yi)運動到下一位置(xi+1,yi+1)的路程時,如果揀貨員需要繞過貨架,如圖4所示,那么當前位置和下一位置同時滿足以下條件:①當前位置和下一位置在同一排;②當前位置和下一位置不在同一豎直過道的一側或兩側。

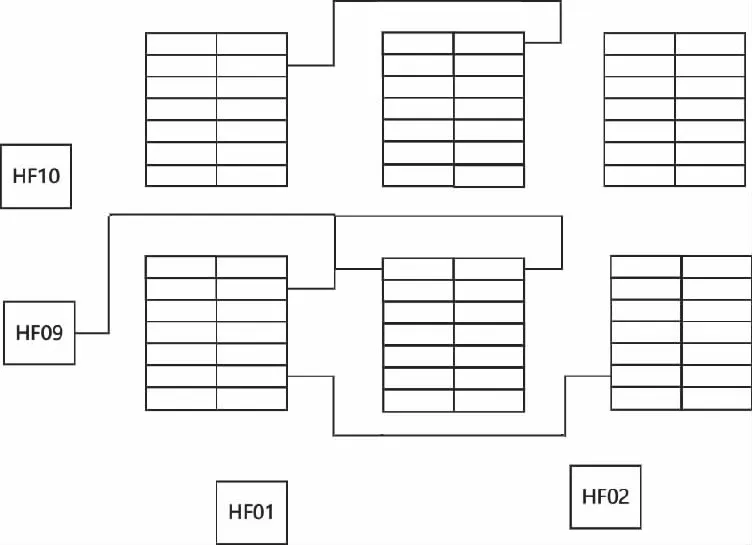
圖4 揀貨員從當前位置運動到下一位置的路徑示意圖

由于揀貨員在繞過貨架時,可從貨架上方繞過,也可從貨架下方繞過,所以選擇它們中最短的路程。此時,揀貨員的路程可表示為:

D(i,i+1)=|xi-xi+1|+min{ytop,ybottom}+(2n+2)×bias

(4)

其中,n為“N”型路線的個數;ytop和ybottom分別為從貨架上方繞過和從貨架下方繞過的總縱向距離,且滿足以下關系:

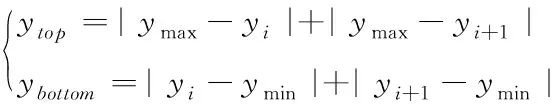
(5)

其中,ymax和ymin分別表示貨格所在貨架的最大和最小縱坐標。

4 揀貨員路徑優化

4.1 改進的遺傳算法

由于本文的倉庫規模較大,直接從全部貨格和復核臺中查找揀貨員當前位置和下一位置并計算二者之間的距離,這將導致求解過程中消耗大量時間。為此,本文在計算適應度時,引入了距離查找表來縮短程序運行時間。具體的過程如下:

1)編碼

對于單任務而言,隨機起始復核臺和終止復核臺,分別置于染色體的首部和尾部,任務涉及到的貨格隨機置于染色體的中間,以此作為該任務的潛在路徑,如圖5所示。對于多任務而言,將多個任務的染色體依次拼接作為一個染色體即可,如圖6所示。

復核臺貨格1…貨格n復核臺

圖6 多任務的編碼

2)查找表

本文提及的倉庫模型共包含3000個貨格和13個復核臺,倉庫規模較大。計算揀貨員從當前位置到下一位置的路程時,如果采用先從整個倉庫模型中查取當前位置和下一位置的坐標,再計算二者之間的距離這一策略,那么這將消耗大量的時間。為了避免上述問題,本文先將揀貨員任務中所涉及的貨格和復核臺選出,然后計算任意貨格與貨格、貨格與復核臺之間的距離,最后以此建立相應的距離查找表。

3)適應度

對染色體的優劣進行評價時,本文采用的衡量標準如下

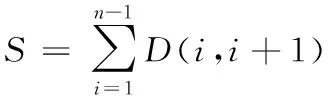
(6)

其中,n為染色體的長度,即該路徑中復核臺和貨架的總數;D(i,i+1) 為第i個復核臺或者貨格和第i+1個復核臺或者貨格間的距離,該距離從距離查找表中獲得。

4)選擇

利用選擇操作中傳統的輪盤賭,選擇出適應度小的染色體作為子代。

5)交叉

交叉分為兩種情況:(1)針對一個染色體,對一個任務內的隨機的兩個貨格進行換位;(2)針對不同染色體,對應位置的復核臺進行交叉。本文通過交叉閾值來決定染色體交叉時,會發生上述情況中的哪一種。

6)變異

通過變異閾值,決定染色體是否發生變異。如果染色體發生變異,那么用重新初始化的染色體替代該染色體。

4.2 倉庫揀貨員多任務路徑優化策略

假設一個揀貨員執行一次任務需要訪問2個復核臺和n個貨格。以上述遺傳算法為基礎,本文提出以下三種策略來求解一個揀貨員的m個任務的最短路徑:

方法1:采用m次單目標規劃。采用上述遺傳算法的單任務編碼,染色體長度為n+2,含有1個適應度,共執行m次;

方法2:采用單目標規劃。采用上述遺傳算法的多任務編碼,染色體長度為m(n+1)+1,含有1個適應度,共執行1次;

方法3:采用多目標規劃。采用NSGA-Ⅱ算法,編碼方式為多任務編碼,染色體長度為m(n+1)+1,含有m個適應度,共執行1次。

5 實驗結果

本文選取了3個揀貨員作為實驗對象,并設定每個揀貨員共執行3個任務,每個任務包含2個復核臺和20個貨格。為了簡化實驗,假設只有復核臺FH03和FH11正常工作。實驗所需原數據如表1所示。

表1 實驗數據

表2為利用遺傳算法求解揀貨員單任務時是否采用距離查找表迭500次的耗時結果。從該表可以看出,采用距離查找表后,可將求解耗時縮小100多倍。

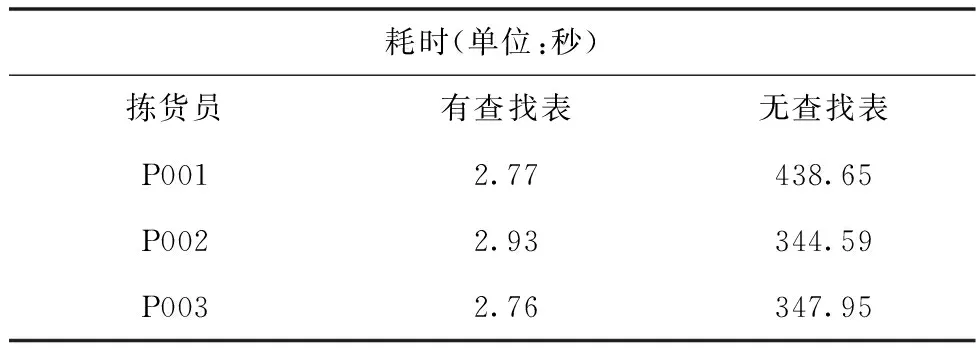
表2 是否采用距離查找表的耗時比較

對于上述求解倉庫揀貨員多任務路徑的三種策略所涉及到的參數均相同:運行一次算法的最大迭代次數為1500次,變異閾值為0.1,交叉閾值為0.5。此外,三種策略在計算適應度時,均采用了距離查找表,且它們的選擇、交叉、變異方式相同。三種策略求得的最短距離和耗時如表3所示。

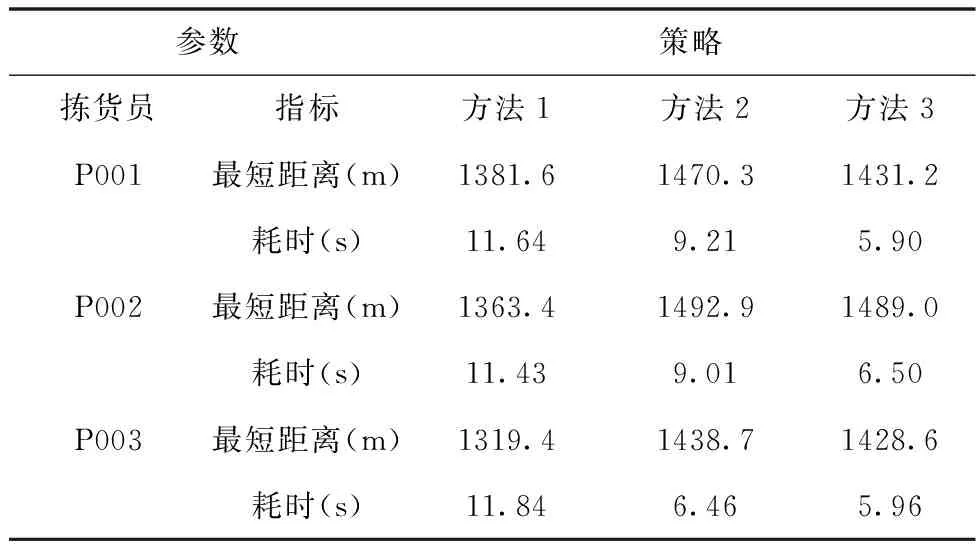
表3 不同策略下的實驗結果比較

從表3可以看出,對于3個揀貨員而言,方法1雖然耗時較長,但是它更利于發現揀貨員多任務時的最短路徑。為了探究其原因,本文將3個揀貨員在不同策略下的求解過程可視化,如圖7所示。以揀貨員P001為例,方法1收斂速度較快;方法2由于染色體的長度太長,所以收斂的速度較慢;方法3很難同時找到三個任務的最短路徑,對于任務T0001迭代了1500次后,仍未收斂,這導致了該方法所得到的結果最差。其他揀貨員亦是如此。方法1所求的最短路徑如表4所示。

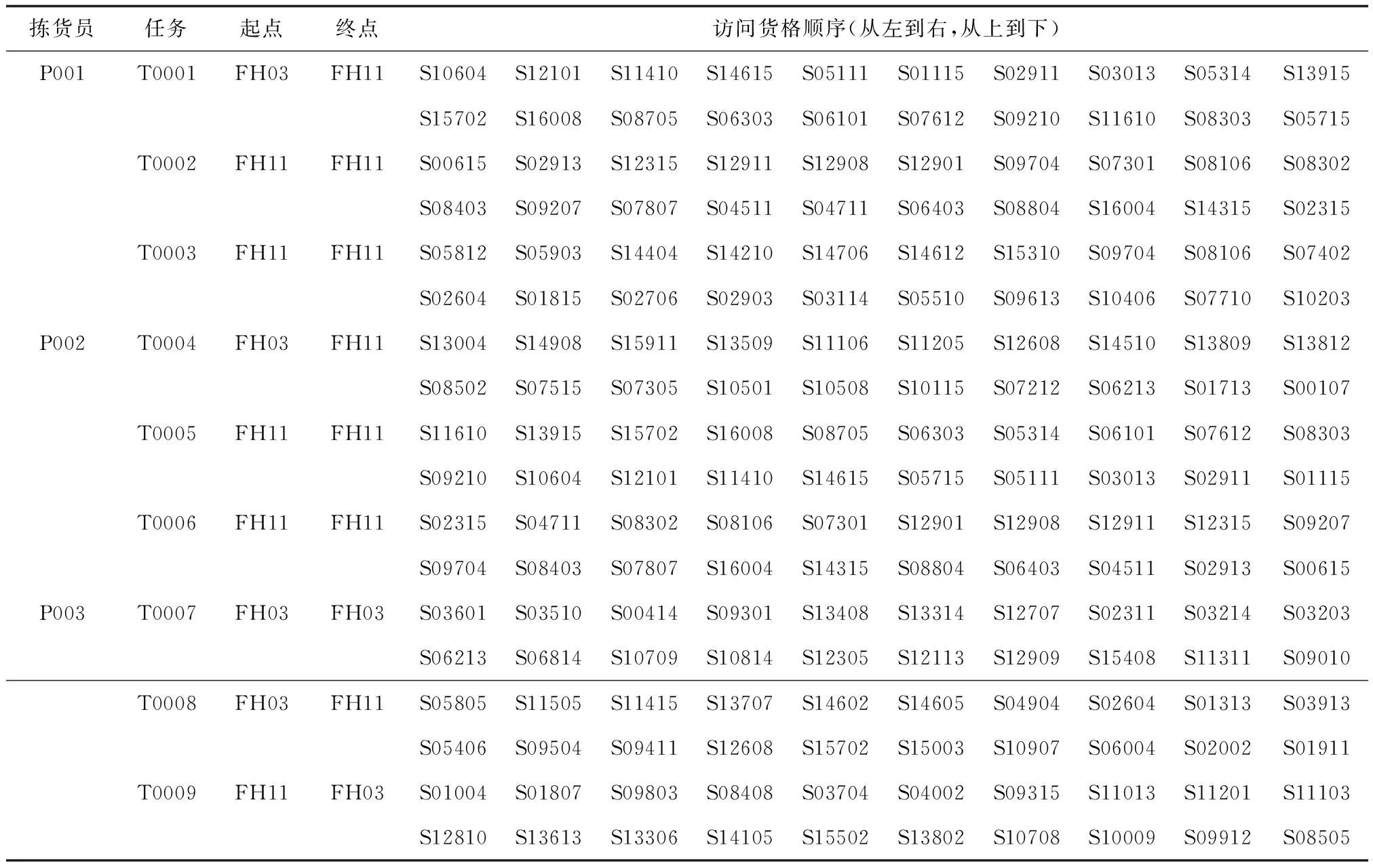
表4 基于方法1的揀貨員的最短路徑

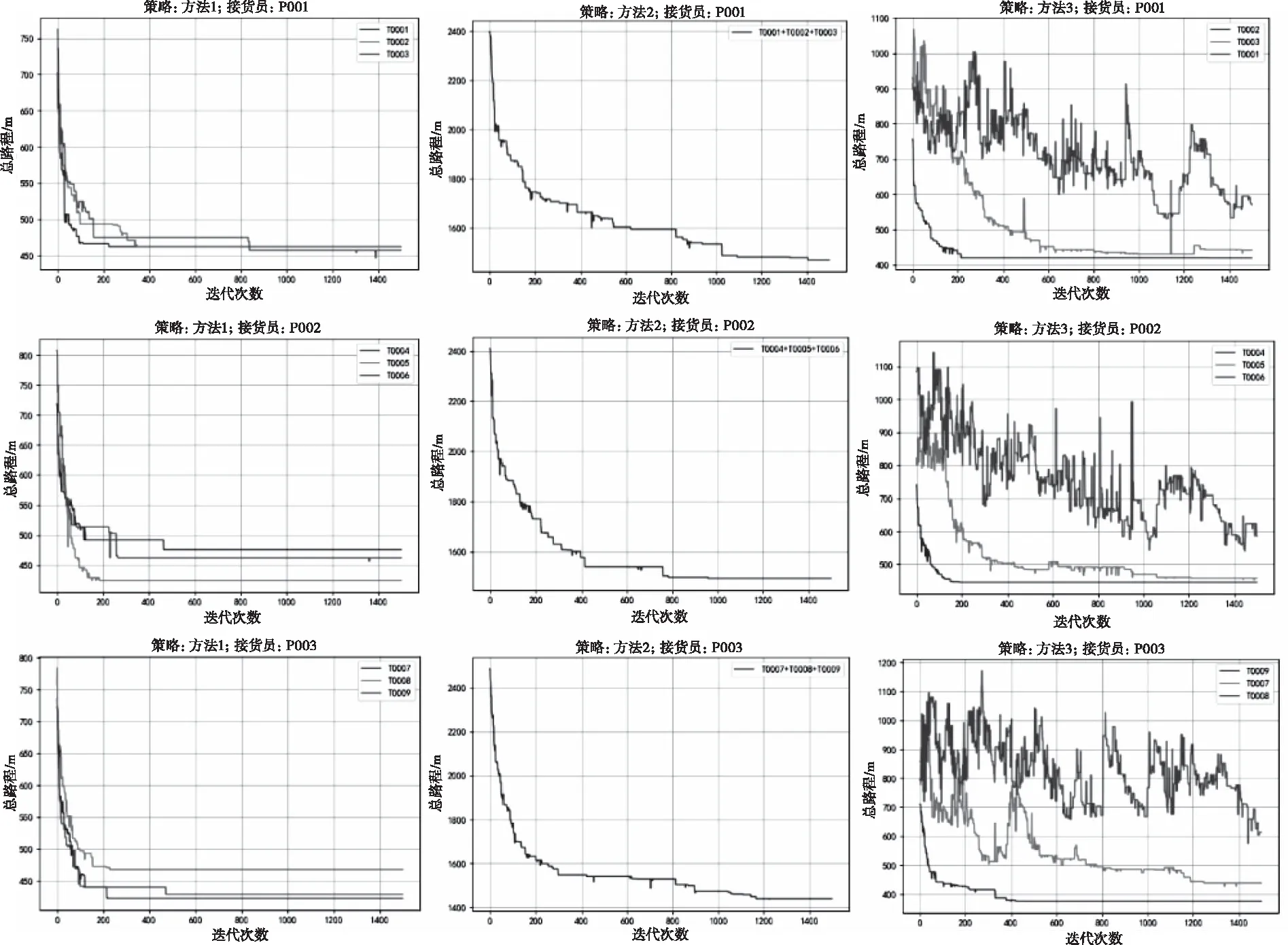
圖7 基于三種方法的3位接貨員最短路徑求解過程

6 結束語

本文總結了揀貨員揀貨時從當前位置運動到下一位置時的路程計算的基本規律。對于較大的倉庫,為了避免因查找位置坐標而導致計算兩點間的距離消耗大量時間,本文先將所涉及的位置坐標選出,計算任意兩位置間的距離,然后建立了距離查找表。提出了利用遺傳算法,采用多次單目標規劃、單目標規劃、多目標規劃三種計算揀貨員在多任務情況下最短路徑的策略。最后,通過實驗驗證了多次單目標規劃效果最優。本文所提的方案能有效解決實際中規模較大的倉庫的路徑優化問題。