基于推理能力發展的數學例題教學研究

尤維明

[摘? 要] 《義務教育數學課程標準（2011年版）》中，將推理能力作為數學核心素養的六要素之一，由此確定了推理能力的重要地位. 文章以一道關于圓的綜合題的教學為例，從解題障礙成因分析出發，具體從以下幾方面展開討論：初步審題，找出有價值的信息;緊扣目標，確定解題的突破口;驗證猜想，促進推理能力發展;畫圖分析，凸顯圖形依賴關系;及時反思，積累解題經驗.

[關鍵詞] 推理能力;例題教學;圓;解題經驗

史寧中教授提出：抽象、推理、模型是數學發展所依賴的主要思想，其中，推理能力的培養不能脫離具體的教學活動的支撐[1]. 良好的數學推理能力形成于知識的學習過程，數學思想方法的滲透過程以及數學問題的解決過程中，學生在教師的引導下逐步積累、領悟、內省而形成各種能力. 至于教師“教什么”“怎么教”對學生的個人發展有著直接影響.

例題教學是數學教學的重要組成部分，然而在現實教學中卻有部分教師存在“重解題，輕過程”的行為，淡化了對學生數學推理能力的培養意識. 其實，通過對問題的觀察、思考、拓展不僅能幫助學生領悟解題的要領，更重要的是能培養學生的數學推理能力.

原題呈現

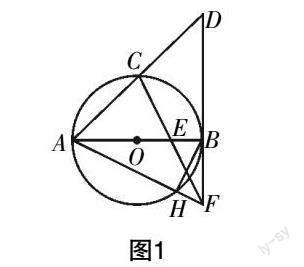
如圖1所示，AB為☉O的直徑，點C為圓弧AB的中點，BD為☉O的切線，交AC的延長線于點D，點E為OB的中點，CE的延長線與切線BD相交于點F，AF與☉O相交于點H，連結HB.

（1）求證：AC=CD;

（2）如果OB=2，求HB的長.

學生在自主解題過程中，主要存在以下幾個問題：①只能根據已知條件提煉出部分簡單結論;②思維卡殼，不會求BF的長;③因為不會求BF的長，就憑借直覺猜想∠FAB=30°，并應用該猜想進行推理，形成錯誤結論;④雖然正確解題，但在添加輔助線（連結OC）上花費了過多時間.

本班學生的認知屬于中等偏上的水平，學生在解決本題過程中所暴露出來的問題具有典型性. 結合學生的認識水平與解題狀況的分析，可以看出不同層次水平的學生在推理能力上有著顯著差異，這也給筆者帶來了一個啟示，即面對有一定難度的關于圓的綜合問題，學生的解題思維需要經歷一個復雜且曲折的過程，而非一氣呵成那么簡單.

本題解題障礙的成因分析

1. 題目本身綜合性高

一般情況下，關于圓的綜合類問題的設計，常以圓為整個問題的背景，綜合考查學生對幾何知識的掌握程度，對學生的幾何直觀能力、推理能力以及運算能力的要求較高，同時還要考查學生解題過程中對數學思想方法的領悟與應用，并對幾何模型的建構提出了要求.

觀察本題，發現題目不僅涉及與圓相關的各種概念，如直徑、弦、弧與切線等，還應用到各種原理，如圓周角定理、切線性質、全等三角形的判定定理、等腰三角形的判定定理與性質以及勾股定理等. 學生只要對其中一個定理理解得不夠透徹，就會影響整道題的解決效果. 由此可見，本題的綜合程度高、考查范圍廣.

2. 學生解題思維受限

解題過程中，運算會遵循通用的運算法則，程序化的運算特征使得學生遇到運算類問題時有章可循. 然而，綜合性高的幾何問題，學生很難從大腦中提取到程序化的通用解題模板，這就需要學生在題目條件與結論之間建構橋梁，不斷調整解題思路，找出其中的聯系[2].

調整解題思路的過程，并非順流直下或逆流而上的過程，而是不斷觀察、分析、推理的過程，這就需要學生在分析法與綜合法之間不斷地靈活切換. 解決本題時，學生的真實思維經歷了一個艱辛的探索歷程，若思維缺乏一定的高度與寬度，則很難披荊斬棘，覓到突破口.

3. 教師忽視思維教學

課堂中，有些教師會以標準解題過程來掩蓋探索結論的曲折過程. 教師所提供的標準解題過程，往往是基于教師本身認知水平上所呈現的思考與推理. 對于學生而言，因為認知水平的差異，導致思考問題的方式與起點不一樣，最終對教師所呈現的標準解題過程只能說出“其然”，卻無法理解“其所以然”.

面對教師直接呈現的標準解題過程，不少學生會提出這樣的疑惑：“我為什么看不出這個結論？”“老師當時有沒有遇到和我一樣的障礙，當時他是怎么突破的？”“我的思路與老師不一樣，是不是也有可行性？”這些都是需要教師思考面對的問題，只有基于“以生為本”的基礎上進行的引導，才具有實際意義.

積極探索，培養推理能力

基于以上對于解題障礙成因的分析，筆者經過精心思考，設計了以下教學活動，與同行共勉！

1. 初步審題，找出有價值的信息

問題設計：根據本題所提供的條件信息，大家能獲得哪些結論？解題需要應用到哪些條件？怎樣才能充分發揮每個條件的最大作用？

設計意圖 讓學生帶著問題去重新讀題、審題，對題目所提供的條件進行全面分析，結合問題要求，提煉出可能需要用到的數學原理，為建構良好的解題思路鋪路搭橋，而教師在此環節最重要的任務是關注學生審題后的實際反饋情況.

為了幫助學生理清如何提取有用信息的思路，可作如下引導：

問題1 觀察圖1，根據AB為☉O的直徑這個條件，是否可從圓周角定理著手，推導出半圓所對的圓周角為直角的結論？

問題2 根據“BD為☉O的切線，交AC的延長于點D”這個條件，是否可結合圓的切線性質定理，聯想到圓的切線與過切點的半徑為互相垂直的關系？

問題3 結合“點C為圓弧AB的中點”，是否能聯想到等弧所對的弦也是相等的？

問題4 根據“CE的延長線與切線BD相交于點F”這個條件，是否能聯想到全等三角形相關知識？

問題5 根據“AF與☉O相交于點H，連結HB”這個條件，可否聯想到直徑或半圓所對的圓周角是直角？

問題6 根據“點E為BO的中點”這個條件，是否能找出特殊圖形關系？

若學生在思考以上幾個問題過程中，表現出對某個原理比較陌生的狀態，就需要教師放慢教學節奏，與學生一起回顧相關原理，讓學生從本源上理解這些結論的來龍去脈，為解題奠定基礎. 同時，教師還要鼓勵學生勇敢地表達出自己的所思所想，學生在嘗試用數學語言表達的過程中，會不斷地提取信息、整理思路、明晰知識結構.

當然，解決以上問題的過程，未必能全面地提取到每個條件所對應的所有價值，特別是根據“點E為BO的中點”這個條件找出相應的解題價值，確實存在一定難度. 因此，教師應從學生的角度去分析問題，從學生思維的卡殼點出發，引導學生通過觀察、猜想、嘗試、探索與證明等過程，尋找新的突破，學生因親歷整個結論的形成與發展過程，推理能力自然而然地能得到有效提升.

2. 緊扣目標，確定解題的突破口

問題設計：想要求出HB的長度，需要先求出哪些線段的長度？通過剛才的分析，有沒有什么條件沒有發揮其價值？

設計意圖 引導學生根據自己原有的認知結構來探索未知，此問為學生的思維提供了明確的方向，讓學生關注到關鍵圖形間的聯系.

學生對Rt△ABF中，雙垂直的背景并不模式，也明白“知二求三”原理. 問題是題目只提供了AB的長，其他數據并不知曉，因此，如何求出BF的值是解開本題的關鍵.

有了明確的目標，學生再次回過頭來思考“點E為BO的中點”這個條件的實際價值，將此條件與BF建立聯系，可分離出一個重要的基本圖形（見圖2），這為后繼輔助線的添加奠定了基礎.

3. 驗證猜想，促進推理能力發展

問題設計1：對于∠BAF=30°這個猜想是否可以驗證？怎么驗證？

設計意圖 猜想出來的結論并不一定是正確的，驗證是確定其是否合理的唯一方法. 此問的設計，目的是為了讓學生對自己的猜想進行驗證，以確定其是否合理.

學生面對此問，提出了以下兩種驗證方案：

方案1 直接用量角器測量，發現結論并不正確;

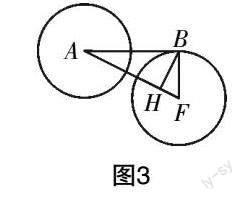
方案2 如圖3，作圖驗證，具體方法為：分別以點A、F為圓心，BF的長度為半徑作圓，所獲得的兩圓并非相切的關系，這與“在直角三角形中，30°角所對的直角邊為斜邊一半”的定理并不匹配，由此可確定這個猜想是錯誤的.

問題設計2：有沒有辦法找出和BF相等的線段？并證明.

設計意圖 這為學生提供了觀察猜想的目標，鼓勵學生通過證明來對猜想進行論證，此時學生會將目光投入到圖形中的等線段、對頂角等特殊條件中，為全等三角形的證明提供依據. 學生因經歷了“方案制定→否定→新方案”的過程，逐漸深化了對問題的理解.

4. 畫圖分析，凸顯圖形依賴關系

問題設計：根據題目所提供的條件順序，嘗試畫示意圖，思考圖中所呈現的線段長度是否確定，為什么？

設計意圖 畫圖能讓學生感知圖形的確定性，從而思考圖形關系對其確定性具有怎樣的影響.

第一步：如圖4，結合已知條件，設AB=2r，那么AC=BC=r;

第二步：如圖5，根據條件“BD為☉O的切線，交AC的延長線于點D”，可知BD=2r;

第三步：如圖6，根據點E為OB的中點這個條件求CE的長，可過點C作AB的垂線，連結OC后可以證得它與AB為垂直的關系，由此可得CE=r;

第四步：如圖7，結合“CE的延長線與切線BD相交于點F”的條件，因為EB=OE=，tan∠BEF=tan∠CEO=2，所以BF=r，也可以根據△BEF?△OEC獲得BF=CO=r.

第五步：如圖8，根據“AF與☉O相交于點H，連結HB”的條件再結合以上結論，在Rt△ABF中，可用r表示AF、AH、BH、FH.

學生通過畫圖，對圖形確定性進行定量分析，在作圖活動過程中融入推理過程，其實就是逐步解三角形的過程. 尤其是第四步，對CE長進行確定與分析時，輔助線OC就自然生成，此時，全等的幾何模型就自然形成了.

以上分析僅局限于對圖象的確定性，不需要求出所有未知幾何元素，我們只要根據解題需要求出相應的未知量即可. 比如在以上分析中，△COE是確定的，由此可得CE的長度，用三角函數來可得出BF的長度. 在△EBF中，結合∠BEF與BE的確定性，可以求出BF的長度. 這是典型的程序化思維模式，其實從全等的角度出發，可直接獲得BF的值，這樣就可以省掉一些計算.

5. 及時反思，積累解題經驗

問題設計1：能否通過畫圖，獲得解決這一類問題的一般程序？

設計意圖 讓學生通過畫圖，感知圖形間的聯系，對圖形確定性形成深刻理解，感知數學轉化思想方法在解題中的重要性，如通過對集中條件的思考，將問題轉化成解三角形的問題.

幾何問題本身就具有一定的開放性特征，若學生的思維隨著條件無限發散出去，而不及時聚合，那么探索過程則缺乏明確的目的性，而影響解題效果[3]. 雖然對關于圓的綜合題的分析，不像數與式那樣具有顯著的程序化特征，但也有一定的規律可循.

問題設計2：解題中，你們是如何突破思維的障礙點的？由此獲得了什么啟示？

設計意圖 再還原思維的障礙點，可以讓學生反思整個解題過程，從中發現自身思維的優缺點，積累良好的數學解題經驗.

每個學生受各種綜合因素的影響，知識儲備有著較大差異，那么在思維障礙的成因上也各不相同，個性化的反思能讓學生充分認識自身的不足. 從而進行有針對性的訓練與調整，為掌握良好的解題技巧奠定基礎.

總之，從本例題教學中，可以看出學生真實的認知水平與思維過程，這種教學模式使得整個課堂充滿了“原生態”的味道，學生因親歷了整個探索與推理的過程，不僅有效地發展了自身的數學思維與推理能力，還促進了數學核心素養的形成與發展.

參考文獻：

[1] 史寧中. 試論數學推理過程的邏輯性——兼論什么是有邏輯的推理[J].數學教育學報，2016，25（04）：1-16，46.

[2] 中華人民共和國教育部. 義務教育數學課程標準（2011年版）[M]. 北京：北京師范大學出版社，2012.

[3] 拉爾夫·泰勒. 課程與教學的基本原理[M]. 施良方，譯. 北京：人民教育出版社，1994.