經(jīng)歷過程 助力發(fā)展

張紅

[摘? 要] 在數(shù)學(xué)教學(xué)中要打破功利教育的束縛，引導(dǎo)學(xué)生多經(jīng)歷一些實(shí)質(zhì)性的思維活動(dòng)，從而讓學(xué)生在學(xué)習(xí)中實(shí)現(xiàn)知識(shí)、能力、態(tài)度的完美統(tǒng)一. 文章以“認(rèn)識(shí)三角形”為例，通過“獨(dú)立思、合作學(xué)”帶領(lǐng)學(xué)生經(jīng)歷三條線段——產(chǎn)生、發(fā)展和應(yīng)用全過程，以此促進(jìn)“教”與“學(xué)”的全面可持續(xù)發(fā)展.

[關(guān)鍵詞] 思維活動(dòng);過程;持續(xù)發(fā)展

在數(shù)學(xué)教學(xué)中，部分教師習(xí)慣依賴經(jīng)驗(yàn)開展教學(xué)活動(dòng). 不過經(jīng)驗(yàn)雖然寶貴，但其本身也存在一定的局限性，若在教學(xué)中僅憑經(jīng)驗(yàn)教學(xué)，數(shù)學(xué)教學(xué)就變成了簡單的機(jī)械重復(fù)，勢必影響學(xué)生思維能力和學(xué)習(xí)能力的提升. 在實(shí)踐教學(xué)中，經(jīng)常會(huì)出現(xiàn)這樣的情況：教師將重難點(diǎn)和易錯(cuò)點(diǎn)內(nèi)容“反復(fù)講、重復(fù)講”，以幫助學(xué)生理解和消化，同時(shí)預(yù)防學(xué)生犯錯(cuò);但在考試中發(fā)現(xiàn)，對于教師“反復(fù)講、重復(fù)講”的內(nèi)容，學(xué)生解題時(shí)依然會(huì)犯錯(cuò)，究其根源就是過程的缺失，并沒有讓學(xué)生將知識(shí)學(xué)懂學(xué)會(huì). 因此，教學(xué)中教師切勿將自己的經(jīng)驗(yàn)強(qiáng)加給學(xué)生，應(yīng)帶領(lǐng)學(xué)生經(jīng)歷一些過程，從而讓學(xué)生將自己的感悟逐漸轉(zhuǎn)化為學(xué)習(xí)的內(nèi)驅(qū)力，以此提升學(xué)習(xí)能力.

筆者以“認(rèn)識(shí)三角形”第2課時(shí)為例，帶領(lǐng)學(xué)生共同經(jīng)歷知識(shí)的形成過程，讓學(xué)生在參與中有所感悟、有所提升.

教學(xué)實(shí)錄

1. 明晰研究對象

師：上節(jié)課我們已經(jīng)學(xué)習(xí)了三角形的概念，明晰了三角形的表示方法和計(jì)數(shù)方法，現(xiàn)在請大家結(jié)合圖1思考如下問題.

若BC邊上有一動(dòng)點(diǎn)P，那么

（1）當(dāng)P運(yùn)動(dòng)到什么位置時(shí)，線段AP平分∠BAC呢？

（2）當(dāng)P運(yùn)動(dòng)到什么位置時(shí)，線段AP平分△ABC的面積呢？

（3）當(dāng)P運(yùn)動(dòng)到什么位置時(shí)，線段AP的長最短呢？

雖然三角形相關(guān)知識(shí)是學(xué)生剛接觸的內(nèi)容，但對于對稱、三角形面積等相關(guān)知識(shí)學(xué)生并不陌生，因此對于以上問題教師讓學(xué)生獨(dú)立思考，尋求解決問題的方法.

師：問題（1）誰來說一說？

生1：對于問題（1），若線段AP所在的直線為∠BAC的對稱軸時(shí)，此時(shí)線段AP平分∠BAC.

師：很好，你們認(rèn)同嗎？（學(xué)生紛紛點(diǎn)頭）

師：對于問題（2）呢？

生2：根據(jù)三角形的面積公式，若BP=CP，即點(diǎn)P為線段BC的中點(diǎn)時(shí)，線段AP能平分△ABC的面積.

師：很好. 問題（3）呢？

生3：當(dāng)AP⊥BC時(shí)，此時(shí)線段AP的長最短.

師：大家說得都很好，不過以上線段該如何確定呢？又存在怎樣的數(shù)量關(guān)系和性質(zhì)呢？

設(shè)計(jì)意圖? 教學(xué)中，從學(xué)生的認(rèn)知出發(fā)，以問題為鋪墊引出主題，這樣有利于調(diào)動(dòng)學(xué)生參與的積極性，激發(fā)學(xué)生的求知欲.

2. 借助畫圖形成各線段的概念

師：對于問題（1）中的動(dòng)點(diǎn)P，你認(rèn)為應(yīng)該如何確定呢？

生4：可以通過折疊的方法確定.

生5：可以用量角器測量后確定.

師：很好，請大家任意畫一個(gè)三角形，選擇適合的方法做一做.

學(xué)生動(dòng)手操作，教師巡視操作結(jié)果，待操作完成后，教師讓學(xué)生展示操作結(jié)果并陳述操作過程.

師：現(xiàn)在我們一起研究一下，看看問題（2），點(diǎn)P的位置該如何確定？

生6：與上面的操作方法基本相同，也可以通過折疊法和測量法來確定.

師：很好，現(xiàn)在大家畫一個(gè)三角形體驗(yàn)一下，選擇合適的方法確定點(diǎn)P.

（本環(huán)節(jié)以學(xué)生動(dòng)手操作為主，教師預(yù)留一定的時(shí)間讓學(xué)生動(dòng)手操作，并讓學(xué)生進(jìn)行示范展示）

師：接下來思考一下，問題（3）中的點(diǎn)P該如何確定呢？

（學(xué)生借助折疊法和三角尺確定了點(diǎn)P，通過動(dòng)手操作對以上三條線段有了清晰的認(rèn)識(shí)，為接下來探究各線段的數(shù)量關(guān)系做好鋪墊）

師：以上線段在今后的學(xué)習(xí)中會(huì)經(jīng)常用到，為了便于交流，我們有必要給這些線段起一個(gè)名字，你們認(rèn)為怎么命名會(huì)更方便呢？

設(shè)計(jì)意圖? 對于線段的命名，教師改變了傳統(tǒng)的照本宣科，這樣在教師的指導(dǎo)下，通過互動(dòng)交流最終確認(rèn)名稱并形成相應(yīng)的概念. 雖然互動(dòng)交流會(huì)花費(fèi)一定的時(shí)間，但是通過交流讓學(xué)生參與其中，會(huì)使抽象的概念變得更加生動(dòng)化，更易于學(xué)生理解和接受.

3. 探究區(qū)別與聯(lián)系，明晰數(shù)量關(guān)系

師：想一想三角形有幾條角平分線呢？

生齊聲答：3條.

師：很好，中線和垂線呢？

生齊聲答：3條.

師：三角形的角平分線與角的平分線相同嗎？（學(xué)生思考片刻）

生7：不同，前者為線段，后者為射線.

師：很好，那么三角形的高線和垂線呢？

生8：也不同，前者為線段，后者為直線.

師：很好，雖然有些概念表面上看似乎相同，但是其本質(zhì)及所代表的意義可能有所不同，在學(xué)習(xí)時(shí)不能只關(guān)注表面，而要善于關(guān)注問題的本質(zhì).

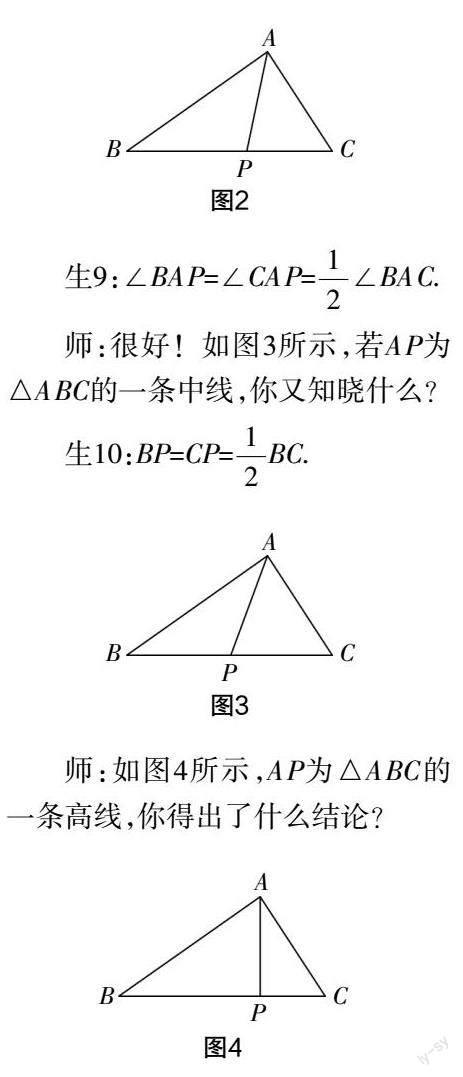
師：如圖2所示，若AP為△ABC的一條角平分線，你可以得出怎樣的數(shù)量關(guān)系？

生9：∠BAP=∠CAP=∠BAC.

師：很好！如圖3所示，若AP為△ABC的一條中線，你又知曉什么？

生10：BP=CP=BC.

師：如圖4所示，AP為△ABC的一條高線，你得出了什么結(jié)論？

生11：若AP為△ABC的一條高線，則AP⊥BC.

生12：∠APB=∠APC=90°.

師：根據(jù)以上的等量關(guān)系，是否可以說明“垂直”“直角”與“90°”屬于同一概念呢？（學(xué)生陷入沉思）

生13：雖然根據(jù)三角形的高線得到了以上等量關(guān)系，但是并不能說明三者相同，它們不屬于同一概念范疇，“垂直”是從位置關(guān)系上進(jìn)行的表達(dá)，“90°”則是從數(shù)量關(guān)系上進(jìn)行的表述，而“直角”是從幾何圖形上進(jìn)行的表達(dá).

師：說得非常好，理解得很到位，其中蘊(yùn)含著“數(shù)”與“形”之間的一種對應(yīng)關(guān)系.

設(shè)計(jì)意圖? 對于以上線段所對應(yīng)的數(shù)量關(guān)系是教學(xué)的一個(gè)重點(diǎn)，教師放慢速度，與學(xué)生一同探究其中蘊(yùn)含的等量關(guān)系及數(shù)學(xué)思想，便于學(xué)生更好地理解概念，為后面應(yīng)用概念解決問題奠基.

4. 自主探究，挖掘“共點(diǎn)”秘密

師：剛剛我們只是畫出了一條三角形的角平分線，現(xiàn)在請大家剪一個(gè)任意三角形，利用折疊法將該三角形的三條角平分線都畫出來，仔細(xì)觀察這三條角平分線，看看它們是否存在什么關(guān)系.

（剛剛學(xué)生已經(jīng)動(dòng)手操作過，同時(shí)又進(jìn)行了示范，因此很快就畫出了三條角平分線）

師：你們有什么發(fā)現(xiàn)？

生14：我發(fā)現(xiàn)三條角平分線相交于同一點(diǎn).

師：很好！現(xiàn)在請大家按照以上步驟分別畫出三條中線，看看它們有何關(guān)系.

（問題給出后，學(xué)生積極操作，很快得出了同樣的結(jié)論，即三角形的三條中線也相交于同一點(diǎn)）

師：我們研究了三角形的角平分線和中線，接下來該研究什么呢？

生齊聲答：三角形的高線.

師：很好. 現(xiàn)在請大家按照以下步驟進(jìn)行操作：

（1）分別畫出銳角三角形ABC、直角三角形DEF和鈍角三角形PQR;

（2）分別畫出這三個(gè)三角形的三條高線;

（3）觀察這三個(gè)三角形三條高線的關(guān)系;

（4）比較這三個(gè)三角形三條高線的交點(diǎn)位置.

（學(xué)生操作，教師巡視，在巡視中發(fā)現(xiàn)有部分學(xué)生在繪制鈍角三角形的三條高線時(shí)存在一些問題，教師給予了單獨(dú)指導(dǎo)）

師：請大家說一說有什么發(fā)現(xiàn).

生15：與前面的兩個(gè)結(jié)論相同，三條高線也相交于同一點(diǎn).

師：它們交點(diǎn)的位置呢？

生16：銳角三角形ABC三條高線的交點(diǎn)在其內(nèi)部;直角三角形DEF三條高線的交點(diǎn)是其頂點(diǎn);鈍角三角形PQR三條高線的交點(diǎn)在其外部.

師：與你們的結(jié)果一致嗎？（學(xué)生點(diǎn)頭表示贊同）

師：很好！剛剛大多數(shù)同學(xué)是利用三角板畫高線，如果利用折疊法可以畫高線嗎？

生17：可以. （學(xué)生示范）

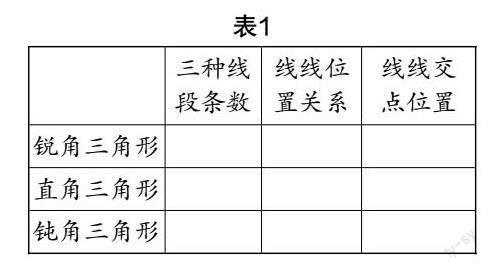
師：結(jié)合以上動(dòng)手操作結(jié)果，請大家完成表1.

教師先讓學(xué)生獨(dú)立完成表1，接下來組織學(xué)生交流反饋，最后教師進(jìn)行點(diǎn)評，完善表格的填寫.

師：大家回憶一下，“共點(diǎn)”的結(jié)論我們是如何發(fā)現(xiàn)的？

生18：折疊和畫圖.

師：很好，畫圖在發(fā)現(xiàn)幾何結(jié)論、證明幾何結(jié)論中都有著重要的應(yīng)用，以上結(jié)論就是借助畫圖獲得的，后面我們會(huì)通過推理的方法進(jìn)行證明，同學(xué)們課后也可以嘗試推理證明.

設(shè)計(jì)意圖? 在教學(xué)中，教師組織學(xué)生通過折疊、畫圖、觀察、總結(jié)等數(shù)學(xué)活動(dòng)最終完成了三角形“三線”知識(shí)體系的建構(gòu). 表面上看以上探究過程只是簡單的操作，但是其中蘊(yùn)含著重要的數(shù)學(xué)思想方法，如分類討論等. 在教學(xué)中，教師應(yīng)多鼓勵(lì)學(xué)生去操作、去觀察、去總結(jié)歸納，進(jìn)而通過親身經(jīng)歷發(fā)現(xiàn)數(shù)學(xué)規(guī)律，掌握數(shù)學(xué)研究方法，以此提升學(xué)生的數(shù)學(xué)學(xué)習(xí)興趣.

5. 恰當(dāng)練習(xí)，助力知識(shí)內(nèi)化

師：相信通過以上探究，大家已經(jīng)對“三線”有了清晰的認(rèn)識(shí)，現(xiàn)在看看以下問題該如何求解. （教師用PPT展示例1）

例1? 如圖5所示，在△ABC中，AD是△ABC的高線，AE是△ABC的角平分線. 已知∠BAC=80°，∠C=40°，求∠DAE的度數(shù).

師：思考一下，想要求∠DAE的度數(shù)，我們需要知道什么呢？

生19：已知∠BAC=80°，如果知道∠DAC和∠EAC的度數(shù)就可以求出∠DAE了.

師：這兩個(gè)角如何求呢？

生20：已知AE是△ABC的角平分線，又∠BAC=80°，可知∠EAC=40°. AD是△ABC的高線，于是∠ADC=90°，又∠C=40°，所以∠DAC=50°.

師：很好，這樣我們就容易得出∠DAE=10°.

師：現(xiàn)在給大家3分鐘時(shí)間，將以上計(jì)算過程書寫完成.

設(shè)計(jì)意圖? 借助簡單的問題讓學(xué)生初步體驗(yàn)知識(shí)的應(yīng)用，通過“用”強(qiáng)化認(rèn)知. 另外，師生交流得到∠DAE=10°后，教師又給學(xué)生一定的時(shí)間完成計(jì)算過程的書寫，以此規(guī)范解題過程，避免解題時(shí)因過程缺失或書寫不規(guī)范而失分.

師：對于例1的運(yùn)算大家都是信手拈來的，可見大家對新知已經(jīng)有了深刻的認(rèn)識(shí). 接下來我們一起探究一下，看看例2該如何求解. （教師用PPT展示例2）

例2? 如圖6所示，在△ABC中，點(diǎn)D，E，F(xiàn)分別為三邊的中點(diǎn). 設(shè)△ABC的面積為S，求△DEF的面積（用S表示）.

例2較例1的難度略有提升，教師沒有急于幫助學(xué)生進(jìn)行分析講解，而是預(yù)留一定的時(shí)間讓學(xué)生獨(dú)立思考，確認(rèn)解題思路，為接下來更好地合作交流奠定基礎(chǔ).

師：由點(diǎn)F是BC的中點(diǎn)，連結(jié)AF，你能夠得到什么？

生21：S=S=S=S.

師：依據(jù)是什么？

生21：等底同高的兩三角形面積相等.

師：很好. 在△AFC中，點(diǎn)E為AC邊的中點(diǎn)，連結(jié)EF，能夠得到什么？

生22：同理可知S=S=S=S.

師：很好，由此可知S=S. △ADE和△DBF的面積分別是多少呢？（學(xué)生思考片刻）

生23：同理可求△DBF的面積為S. 連結(jié)CD，可求得△ADE的面積也為S.

師：很好，這樣我們求得△DEF的面積是多少呢？

生齊聲答：S.

接下來教師預(yù)留時(shí)間讓學(xué)生完善以上的計(jì)算過程，這樣一方面可以幫助學(xué)生規(guī)范解題過程，另一方面可以給基礎(chǔ)較弱的學(xué)生一定的時(shí)間理解和消化，從而實(shí)現(xiàn)全面進(jìn)步.

師：結(jié)合圖6，請大家思考一下，DE與BC存在什么樣的關(guān)系？

生24：平行.

師：說一說理由.

生24：我是通過觀察得出的，應(yīng)該可以證明.

師：很好，觀察是一種直觀猜想，往往能夠?yàn)樘骄刻峁┓较颍贿^其具有一定的主觀性，若想證明該結(jié)論成立需要進(jìn)一步推理. 大家推理一下，DE∥BC是否成立呢？

生25：成立. 根據(jù)以上計(jì)算過程可知S=S，過點(diǎn)D和點(diǎn)E分別作△DBF和△FCE的高線，由底相等、面積相等，可得高線的長相等，于是點(diǎn)D，E到BC的距離相等，故DE∥BC.

師：很好，其實(shí)仔細(xì)觀察圖6還能得出許多結(jié)論，這里我們就不一一探究了，請大家課后思考一下，看看還有哪些發(fā)現(xiàn).

設(shè)計(jì)意圖? 完成例2的計(jì)算后，教師在此基礎(chǔ)上引導(dǎo)學(xué)生進(jìn)一步探索，得到了DE∥BC，由此可以推廣至EF∥AB，DF∥AC. 這樣通過問題的擴(kuò)展既有助于發(fā)散學(xué)生的思維，又為接下來學(xué)生學(xué)習(xí)三角形中線的性質(zhì)及定理做好鋪墊. 數(shù)學(xué)學(xué)習(xí)的過程更多的是一種自我發(fā)現(xiàn)和自主探究的過程，為此在日常教學(xué)中教師要改變單一的“就題論題”，多引導(dǎo)學(xué)生去發(fā)現(xiàn)和探究，以此促進(jìn)學(xué)生自主學(xué)習(xí)能力的提升.

6. 課堂小結(jié)，反思提升

課堂小結(jié)是數(shù)學(xué)教學(xué)的重要一環(huán)，教學(xué)中教師要預(yù)留一定的時(shí)間指導(dǎo)學(xué)生進(jìn)行總結(jié)和歸納，便于學(xué)生更好地把握本節(jié)課的重難點(diǎn)，厘清數(shù)學(xué)知識(shí)的研究方法，提煉出數(shù)學(xué)思想方法，從而通過總結(jié)歸納將活動(dòng)經(jīng)驗(yàn)逐漸轉(zhuǎn)化為學(xué)習(xí)能力，在掌握知識(shí)的基礎(chǔ)上認(rèn)清問題的本質(zhì)，提升教學(xué)有效性.

教學(xué)反思

有時(shí)部分教師在數(shù)學(xué)教學(xué)中表現(xiàn)得過于功利，忽視了結(jié)果形成與應(yīng)用的實(shí)質(zhì)性思維過程，從而影響了全面、和諧的教學(xué)目標(biāo)的落實(shí)，影響了學(xué)生核心素養(yǎng)的發(fā)展，顯然這有悖于教育初衷，不利于學(xué)生發(fā)展.

在本節(jié)課教學(xué)中，教師以學(xué)生熟悉的三角形為載體，通過教師適度引導(dǎo)和學(xué)生自主建構(gòu)共同經(jīng)歷了三種線段產(chǎn)生的過程. 在此過程中，學(xué)生通過動(dòng)手折、動(dòng)手畫既體驗(yàn)了數(shù)學(xué)知識(shí)形成的過程，又感悟了蘊(yùn)含其中的數(shù)量關(guān)系和運(yùn)動(dòng)的觀點(diǎn)，還提煉出了重要的思想方法，不僅揭示了相近概念之間的區(qū)別與聯(lián)系，而且在探索中掌握了數(shù)學(xué)研究方法. 另外，在教學(xué)過程中，教師既從全局出發(fā)引導(dǎo)學(xué)生經(jīng)歷知識(shí)生成、發(fā)展、應(yīng)用的全過程，又不忘一些細(xì)節(jié)的處理，如書寫規(guī)范、小結(jié)、反思等，促進(jìn)了學(xué)生知識(shí)與技能的發(fā)展，使核心素養(yǎng)的培養(yǎng)得以落實(shí).

總之，教學(xué)中教師要從學(xué)生學(xué)情出發(fā)，關(guān)注教學(xué)過程，關(guān)注“三維目標(biāo)”的落實(shí)，為學(xué)生綜合能力全面提升助力.