基于EFPI-FBG 結構的光纖復合傳感器研究

劉冬冬 王 偉 王昆鵬 劉 彬

(1.中國人民解放軍92493 部隊,葫蘆島 125001;2.西安航天動力試驗技術研究所,西安 710100;3.沈陽黎明航空發動機集團有限公司,沈陽 110000;4.哈爾濱工程大學信息與通信工程學院,哈爾濱 150001)

1 引言

實時有效的壓力原位測量在諸多領域都有重要應用前景,如在發動機狀態監測領域,通過壓力信號可及時有效地判斷發動機喘振、燃燒穩定性、循環疲勞等問題[1]。常規壓電、壓阻式敏感器件在發動機運行的高溫場景下,無法穩定開展測試工作,時常出現失效或者損壞現象。隨著光纖傳感技術的不斷發展,光纖傳感器件展現出體積小、耐高溫、抗電磁干擾等諸多優勢[2],可以有效填補傳統敏感器件在惡劣環境下的缺點和不足。膜片式光纖法布里珀羅（F-P）干涉傳感器就是其中的典型代表,近些年獲得了廣泛的研究和關注[3,4]。

1997 年,Kim Myung Gyoo 采用MEMS 工藝研制了一種氮化硅和石英復合薄膜的光纖壓力傳感器,其傳感單元尺寸達到8×8 mm2時,靈敏度可增加1.57 rad／kPa[5]。2005 年,Denis Donlagic 提出的基于SiO2薄膜的光纖EFPI 壓力傳感器可實現（0～1）MPa范圍的壓力測量,分辨率為300 Pa[6]。2019 年,北京理工大學的趙琴琴以硅與特種玻璃為基本單元,使用MEMS 工藝制作光纖壓力傳感器,可實現（0～1）MPa 范圍的壓力測量[7]。在膜片式光纖EFPI 壓力傳感器中,膜片在壓力作用下發生變形,從而引起F-P 腔長發生變化,進而引起F-P 干涉譜的變化,通過檢測干涉譜的變化即可實現對壓力的測量。但在實際應用中,傳感器工作環境的溫度變化將引起材料尺寸和材料熱光系數發生變化,即同樣引起F-P 腔的干涉譜發生變化。因此,傳統EFPI 壓力傳感器存在溫度壓力交叉敏感問題。一種解決方法是進行壓力測量的同時實現對溫度的測量,從而實現溫度影響的消除[8]。因此,在某些需要雙參數測量領域,這一方法得到了較大的關注。

在本文中,研究了一種串聯式EFPI-FBG 結構的壓力—溫度復合傳感器。通過在EFPI 結構的引導光纖上引入FBG 結構,實現對壓力和溫度參數的測量。采用熔融石英材料構建壓力傳感器的敏感單元,提高了傳感器的穩定性,對傳感器的溫度和壓力響應進行了測量,并對試驗結果進行了詳細的討論。研究結果表明,該類型傳感器在溫度壓力雙參數測量中具有廣闊的應用前景。

2 EFPI-FBG 復合傳感器工作原理

2.1 EFPI-FBG 復合傳感器光學原理

入射光Iin進入光纖后,首先通過FBG 傳感結構,其反射光信號為I1,則

式中:fFBG——FBG 結構的反射譜。通過FBG 的透射光I2可表示為

透射光I2從光纖端面出射后,入射到膜片內表面反射,隨后再次耦合進入光纖中,形成干涉光譜I3為

式中:fEFPI——EFPI 結構的反射譜。

I3折返至FBG 傳感結構后,產生透射光I4為

I4與I1疊加,形成最終的出射干涉光譜Iout表示為

式中:R1——FBG 的峰值反射率;λFBG——FBG 的中心波長;c——反射峰的寬度大小;R2——引導光纖進入F-P 腔端面的反射率;R3——F-P 腔敏感膜片的反射率;L——F-P 腔長;λ——入射光的波長。

2.2 EFPI-FBG 復合傳感器結構

所采用的EFPI-FBG 復合傳感器由膜片層、支撐層1、支撐層2、支撐層3、石英管和光纖光柵構成,如圖1 所示。

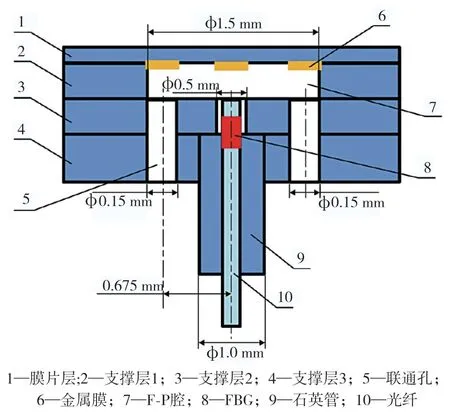
圖1 復合結構光纖傳感器基本結構示意圖Fig.1 Basic structure diagram of composite structure optical fiber sensor

膜片層、支撐層1、支撐層2、支撐層3 的材料均為熔融石英玻璃。采用相同材料的好處是可以避免熱膨脹系數不同帶來的應力不匹配,從而提高傳感器的性能穩定性。作為壓力敏感結構的膜片層厚度為100 μm,支撐層1 和支撐層2 厚度為300 μm,支撐層3 厚度為500 μm。支撐層1 中間的通孔尺寸（?1.5 mm）決定了壓力敏感膜片的有效直徑,從而決定了傳感器的壓力靈敏度。支撐層2 提供石英毛細管的阻擋作用,其中間通孔（?1.5 mm）用于通過光纖結構;支撐層3 提供石英毛細管的支撐,其中間通孔直徑為1 mm,與所采用的石英毛細管直徑相匹配。引導光纖經由石英管固定,光纖端面和膜片的內表面之間組成F-P 腔結構,在靠近光纖端面處刻寫FBG 結構。在支撐層2 和支撐層3 同時加工了兩個對稱的圓形聯通孔（?0.15 mm）結構,聯通孔中心距支撐層中心0.675 mm,用于連通F-P 腔和外部大氣。

2.3 EFPI-FBG 復合傳感器壓力敏感機理

采用邊緣固定的圓形平板作為壓力敏感膜片。假設敏感膜片半徑為R,厚度為d,其楊氏模量為E,則在均勻壓力P作用下,膜片中心受迫形變量σ0可以表示為

式中:v——膜片材料的楊氏模量。所采用的熔融石英材料尺寸為d=100 μm,R=0.75 mm,計算可得其膜片中心位置的壓力靈敏度約為0.8 μm／MPa。

2.4 EFPI-FBG 復合傳感器溫度敏感機理

外界溫度發生變化時,熱光效應及熱膨脹效應會改變FBG 傳感結構的光柵周期和有效折射率,促使中心波長產生漂移現象。其偏移量滿足

式中:λFBG——中心波長;ΔλFBG——中心波長變化量;Λ——光柵周期;ΔΛ——光柵周期變化量;ne——有效折射率;Δne——有效折射率變化量;α——熱膨脹系數;β——熱光系數;ΔTFBG——外界溫度變化量。因此,光纖光柵的溫度靈敏度系數可表示為KT=α+β。常溫下,普通石英材質的摻鍺光纖熱膨脹系數α=0.5×10-6／℃、熱光系數β=8.3×10-6／℃,則KT=8.8×10-6／℃,在本文中,λFBG=1 550 nm,對應溫度靈敏度理論值為13.6 pm／℃。

利用公式（5）進行仿真,得到傳感器干涉譜信號如圖2 所示,假設波長的有效區間范圍為（1 520～1 565）nm,對FBG 而言,R1=90%,λFBG=1 550 nm,3 dB 帶寬為0.3 nm;對于F-P 結構而言,R2=R3=4%,L=300 mm。可以發現,其反射譜明顯由兩部分組成,分別是用于壓力測量的雙光束干涉區域和用于溫度測量的FBG 區域。

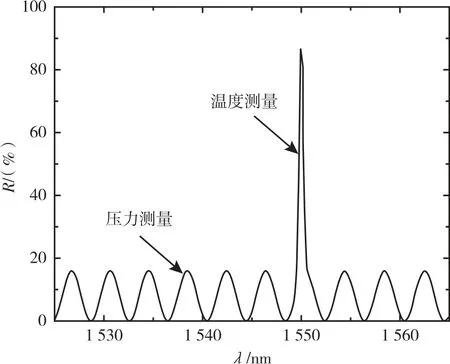
圖2 EFPI-FBG 復合傳感器干涉譜仿真信號Fig.2 EFPI-FBG composite sensor interference spectrum simulation signal

在實際情形中,EFPI-FBG 復合傳感器的腔長變化ΔL和中心波長的變化ΔλFBG同時受到外界壓力變化ΔP及溫度ΔT變化的影響,因此,它們之間滿足

式中:A11——F-P 腔的壓力靈敏度;A12——F-P 腔的溫度交叉靈敏度;A21——FBG 的壓力交叉靈敏度;A22——FBG 的溫度靈敏度。對于特定的傳感器,上述四個參數可以通過試驗進行校準。在測量得到F-P 腔的腔長變化和FBG 的中心波長變化后,可以計算得到外界的壓力和溫度變化。

3 EFPI-FBG 復合傳感器加工

EFPI-FBG 傳感單元制作流程如圖3 所示,步驟為:（1）定制三塊不同規格的石英基片a1、b1、c1,并將表面進行清潔處理;（2）采用機械刻蝕工藝分別在基片上加工對應的通孔結構,得到a2、b2、c2;（3）采用飛秒激光將三層結構焊接成支撐結構e;（4）制作特殊規格的石英敏感膜片d,將其與支撐結構e 焊接牢固,組成與外部聯通的結構f;（5）在石英膜片內表面,采用電子束蒸鍍的方法制作金屬銀增反層,得到g 結構;（6）從背板插入石英插芯并固定后（h）,插入預先刻寫完成的FBG 單模光纖進行高溫固化,完成傳感單元i 的制備。圖4（a）為飛秒激光鍵合工藝制備完成的傳感器敏感單元。圖4（a）中的插圖是利用掃面電鏡測量得到的鍵合區域,可以發現石英層之間焊接的區域實現了良好的鍵合;而未焊接的部分有空隙存在,這正是石英片上彩虹狀條紋產生的原因。圖4（b）為完成的傳感單元實物。

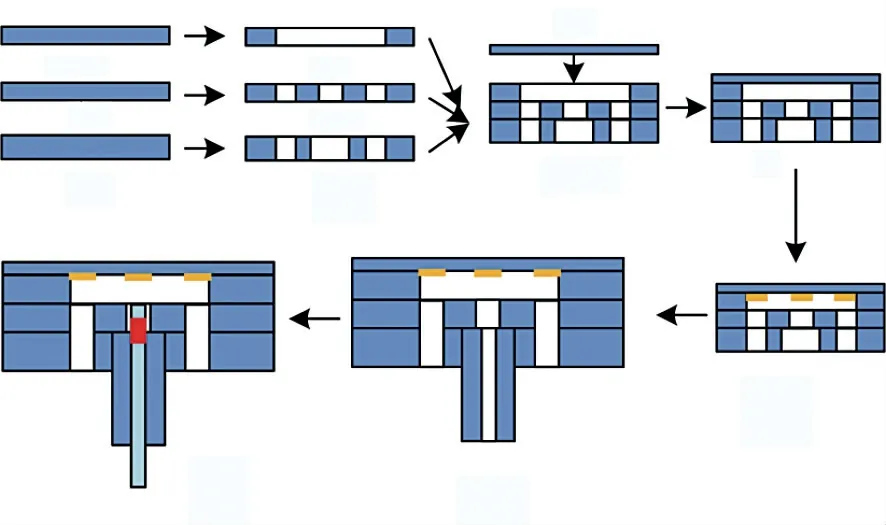
圖3 EFPI-FBG 傳感單元制作流程示意圖Fig.3 Schematic diagram of EFPI-FBG sensing unit manufacturing process

圖4 制備完成的傳感單元實物圖Fig.4 Prepared physical drawing of sensing unit

4 光纖EFPI-FBG 復合傳感器性能測試

光纖傳感器測試系統如圖5 所示。解調系統由寬帶激光器（LSB-ASE-C,OPEAK,波長為1 530～1 560 nm）、環形器、待測光纖傳感器、光譜分析儀（AQ6370C,YOKOGAWA）和測試計算機組成。激光器寬帶信號經環形器進入光纖傳感器,其反射光經環形器后入射到光譜分析儀,計算機對采集的干涉譜數據進行解算。右側虛線框內為測試用設備,電熱板（溫度控制最大允許誤差為±1℃）用于對光纖傳感器的溫度響應進行測試,壓力罐、精密調壓閥（IR2020-02BG,最大允許誤差為±0.2% FS）及氮氣罐用于對光纖傳感器進行壓力測試。精密調壓閥的壓力調整范圍為（0～0.8）MPa。電熱板的加熱區間是50℃～300℃。需要說明的是,由于條件限制,所采樣的溫度和壓力控制單元的控制誤差會不可避免地影響傳感器性能,導致測量結果出現偏差。在測試過程中,需要通過延長溫度和壓力穩定時間以及多次測量的方式盡可能降低其影響。在傳感器的后續研究中,還應采用標準設備對傳感器性能進行標定。

圖5 光纖傳感器測試系統示意圖Fig.5 Composition diagram of optical fiber sensor test system

4.1 干涉譜信號及初始腔長

利用圖5 所述裝置進行測量,得到常溫、常壓狀態下的干涉譜,如圖6 所示。與仿真結果不同的地方在于FBG 的反射譜附近出現了較多的毛刺現象,其可能的原因是FBG 的有效區域同光纖端面相隔較近,FBG 區域同光纖端面的反射光之間發生了寄生干涉現象。當采樣點數較少時,該現象消失。

圖6 光纖傳感器干涉光譜測量結果Fig.6 Measurement results of interference spectrum of optical fiber sensor

分析可知,圖2 和圖6 中雙光束干涉條紋的相鄰兩個波峰或波谷之間的相位差為2π,因此可以計算F-P 腔的腔長Lcav為

式中:λ1和λ2——分別為干涉條紋相鄰兩個波谷（或波峰）處的波長值。取λ1=1 530.956 nm,λ2=1 535.772 nm,計算可得傳感器的初始腔長為244.102 μm。

對于干涉譜中特定某個波峰或者波谷信號而言,根據公式（6）可知,其波長值將隨著F-P 腔長的變化而變化。F-P 腔長的相對變化量ΔLcav與波峰或者波谷處波長的相對變化量Δλ滿足

因此,根據測量得到干涉譜中特定波峰或者波谷位置的波長相對變化量,可以計算得到腔長的相對變化量,該方法稱為單峰測量法。

利用光譜儀的峰值提取功能,可以直接讀取得到FBG 的中心波長為1 549.932 nm。將此結果作為傳感器在常溫常壓下的初始狀態。

4.2 EFPI-FBG 傳感器壓力響應測試結果

首先,對加工得到傳感器的壓力穩定性進行測試。將壓力保持在0.6 MPa 處,每隔1 min 采集一次光譜數據,測試結果如圖7 所示。在測試過程中,光譜采集區間設置為1 525～1 575 nm,采集點數為12 501。可見,傳感器光譜重復性良好。將1 538 nm處的光譜信號放大,可以發現其波長只偏移了約30 pm。由于光譜的偏移有可能來自于所施加的壓力自身的不穩定,因此,可以認為加工得到的壓力傳感器具有良好的穩定性。

圖7 0.6 MPa 作用下的傳感器穩定性測試結果Fig.7 Sensor stability test results under action of 0.6 MPa

對傳感器的壓力響應進行測試。將傳感器安裝在壓力罐中,從常壓（0 MPa）開始,以0.1 MPa 為步長,逐漸加壓至0.8 MPa,然后再以相同步長降壓至0 MPa。重復3 次,在每個壓力點處都記錄一次光譜數據,測試結果如圖8 所示。可以發現,在升壓過程中的干涉譜信號發生漂移現象。為了更好的觀察F-P 腔光譜的偏移,將1 535～1 540 nm 波長范圍內的干涉譜信號進行放大,如圖8 中虛線框中子圖（縱坐標已轉換為對數形式）所示,可以明顯看出光譜紅移的效果。利用單峰測量法,通過監測波谷處波長的變化,即可得到腔長的變化值。

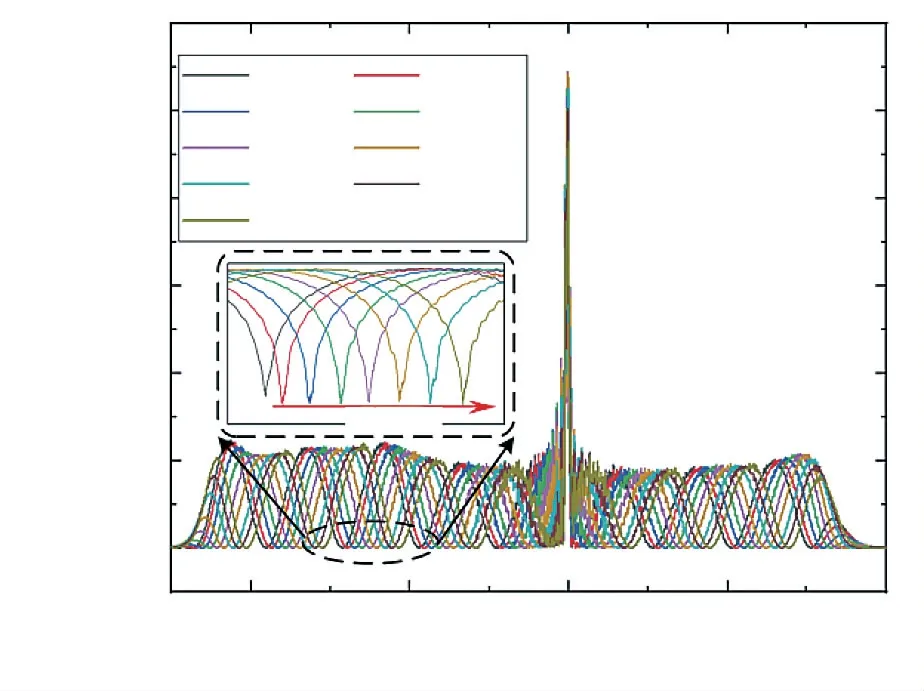
圖8 升壓作用下傳感器響應測試結果Fig.8 Sensor response test results under boost

升降壓過程中0.6 MPa 處的光譜信號及其局部放大圖如圖9 所示。可以發現,光譜信號具有較高的重復性。將1 538 nm 波谷處的光譜放大后可以發現此時波長差值不超過0.166 nm。利用單峰追蹤法,可以得到在此壓力處的腔長變化值不超過26.2 nm。

圖9 三次升降壓作用過程中傳感器重復性測試結果Fig.9 Repeatability test results of sensor during three pressure rise and fall

三次循環測試后EFPI 腔長隨壓力變化的趨勢如圖10 所示,圖中同時標出了測試結果的均值及其線性擬合結果。可以得到測量腔長動態范圍輸出為0.569 μm。參考《GB／T 15478-2015 壓力傳感器性能試驗方法》中規定的重復性定義,對傳感器的壓力響應重復性進行計算。三次壓力升降過程中,最大標準差為0.009 8 μm,取重復性系數為2,則壓力測試的重復性為3.44%。計算可得壓力傳感部分最大的非線性誤差為0.021 μm,線性度為3.56%;其遲滯誤差出現在0.5 MPa 處,計算可得此時對應的遲滯誤差為1.27%。傳感器最大允許誤差由重復性誤差、非線性誤差和遲滯誤差共同決定,計算可得所實現的傳感器最大允許誤差為4.12% Fs。相比現有的傳感器,所實現的傳感器最大允許誤差尚不理想。根據計算過程可知,傳感器的重復性和非線性誤差均較大,其可能的原因包括所用測試設備自身的重復性和準確性,同時也來自于所采用的傳感器腔長解調算法。根據斜率可得傳感器的壓力靈敏度A11為-0.729 μm／MPa。實際測量得到的傳感器壓力靈敏度小于理論值,可能的原因在于膜片的厚度、中間孔的直徑等存在加工誤差。

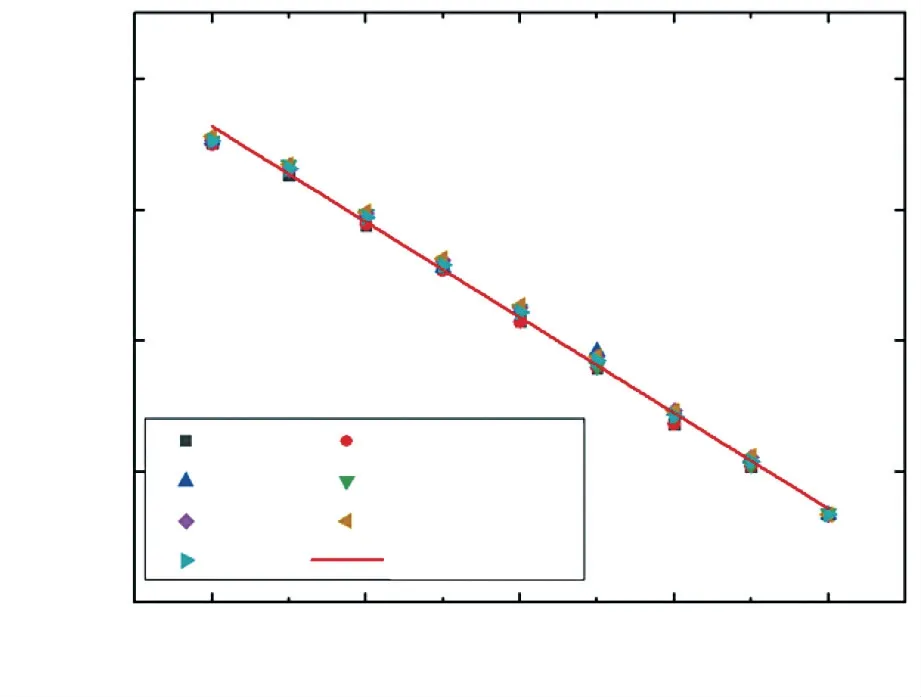
圖10 EFPI-FBG 復合壓力響應測試結果Fig.10 EFPI-FBG composite pressure response measurement results

雖然FBG 的封裝結構使其免于受到應力的影響,但根據公式（5）可知,FBG 的中心波長同時也受到F-P 腔長的調制。因此,FBG 中心波長對壓力變化的敏感情況進行了測試,結果如圖11（a）所示。測試結果表明,壓力的不斷升高使測試樣品FBG 中心波長呈現漸大趨勢。壓力和溫度之間的擬合結果如圖11（b）所示,其擬合曲線斜率即FBG 中心波長的壓力靈敏度為0.071 nm／MPa,表明FBG 的中心波長受到了F-P 腔長的調制。

圖11 FBG 中心波長隨壓力變化測試結果Fig.11 Test results of FBG central wavelength varying with pressure

4.3 EFPI-FBG 復合傳感器溫度響應測試結果

將傳感器置于加熱板上,改變其工作溫度。測試溫度范圍為50℃～200℃,每次數據記錄間隔25℃（穩定30 min）。保持大氣壓狀態,進行不間斷升降溫測試,將一次升降溫作為一組測試行程,共進行三組,測試結果如圖12 所示,其FBG 的中心波長隨溫度變化趨勢如圖中虛線框內所示。可以看出,溫度的升高可使中心波長不斷增加。

圖12 FBG 反射譜中心波長隨溫度變化測量值Fig.12 Measured value of central wavelength of FBG reflection spectrum varying with temperature

畫出三次測試結果的平均值及對應的線性擬合結果,如圖13 所示。FBG 在三次升降溫環節中的滿量程最大輸出為1.558 nm。同樣參考壓力傳感器的重復性概念對FBG 測量結果的重復性進行表征。三次正反行程測量中,正向（0.021 nm）和反向（0.048 nm）最大重復性誤差均出現在175℃處,計算可得該點的標準差為0.02 nm。取重復性系數為2,則溫度測試重復性為2.57%。通過擬合計算,溫度傳感部分的最大非線性誤差為0.027 nm,則可得線性度為1.73%。擬合結果的皮爾遜系數為0.999,表明FBG 的中心波長同溫度之間存在良好的線性關系,擬合曲線的斜率表明FBG 傳感器的溫度靈敏度為0.009 nm／℃。

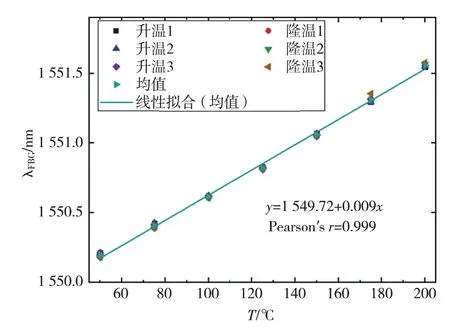
圖13 光纖傳感器溫度傳感重復測試數據結果Fig.13 Repeated test data results of optical fiber sensor temperature sensing

由于材料熱膨脹等原因,溫度變化會影響F-P腔腔長,從而影響壓力測量。因此,將F-P 腔腔長對溫度變化敏感情況進行了測試,結果如圖14 所示。可見,溫度的升高會使F-P 腔腔長逐漸變大。而當溫度升高之后腔長的離散性增加,其可能的原因是傳感器封裝中所采用的高溫膠性質不穩定。在后續的研究中,將采用具有更高性質的無機膠結構或進行激光焊接。測試結果中,擬合曲線的皮爾遜系數為0.986,體現出高度線性相關性,此項交叉敏感影響不可忽略。擬合曲線斜率表明,F-P 腔腔長受溫度變化影響約為22 nm／℃。

圖14 F-P 腔腔長與溫度變化的關系曲線Fig.14 Relationship curve between cavity length and temperature of F-P cavity

根據上述測試結果,可以得到得EFPI-FBG 復合傳感器的靈敏度矩陣關系式為

通過該矩陣關系式,可以由FBG 中心波長與F-P腔腔長變化直接計算得到壓力和溫度變化量,較好地解決了工程實際應用的快速測量問題。然而,從實際應用角度來說,矩陣中的相關系數A12和A21應盡可能趨近于0,從而降低交叉敏感影響,這也為后續深化研究提供了方向。

5 結束語

研究了一種基于EFPI-FBG 串聯結構的光纖復合傳感器。利用EFPI 結構實現對于壓力信號的測量,利用FBG 結構實現對于溫度信號的測量。傳感器整體結構為熔融石英構成,并采用飛秒激光焊接的方式進行傳感器的封裝。通過分析傳感器的工作原理,搭建解調裝置,對制作的EFPI-FBG 傳感器結構進行測試與分析。傳感器膜片結構的壓力靈敏度約為-0.729 μm／MPa,其F-P 腔的溫度交叉靈敏度為0.022 μm／℃。FBG 結構的溫度靈敏度為0.009 nm／℃,其壓力交叉靈敏度為0.071 nm／MPa。所研究的EFPI-FBG 復合傳感器有望應用于需要壓力—溫度雙參數測量的領域。