孔系自參考位置度最小區(qū)域的一般化判別方法

秦玲 唐哲敏 程彬彬

摘??要：評(píng)定孔系自參考位置度時(shí)，沒(méi)有一般化的判別方法來(lái)裁定某個(gè)算法構(gòu)造或找到的誤差邊界是否滿(mǎn)足最小區(qū)域條件。針對(duì)這一問(wèn)題，研究基于邊界點(diǎn)的孔系自參考位置度最小區(qū)域一般化判別方法。分析了孔系的測(cè)點(diǎn)集與誤差邊界的相對(duì)空間關(guān)系，建立了孔系位置度最小區(qū)域模型；分析了最小區(qū)域判別邏輯的基本數(shù)理形式及其基本推論；建立邊界點(diǎn)的基本運(yùn)動(dòng)矩陣，并將最小區(qū)域的判別邏輯問(wèn)題轉(zhuǎn)化為等效的基于矩陣的一般化判別方法。最后通過(guò)一個(gè)實(shí)例驗(yàn)證了提出的孔系自參考位置度最小區(qū)域一般化判別方法。

關(guān)鍵詞：判別方法??位置度??孔系??自參考??誤差評(píng)定

中圖分類(lèi)號(hào)：TH161?????文獻(xiàn)標(biāo)識(shí)碼：A

A?Generalized?Discrimination?Method?for?the?Minimum?Zone?of?Self-Reference?Positional?Tolerance?of?the?Pattern?of?Holes

QIN?Ling1??TANG?Zhemin2*?CHENG?Binbin1

（1.?Guilin?Institute?of?Information?Technology，?Guilin，?Guangxi?Zhuang?Autonomous?Region，?541004?China;

2.?Guilin?University?of?Electronic?Technology，?Guilin，?Guangxi?Zhuang?Autonomous?Region，?541004?China）

Abstract：?When?evaluating?the?self-reference?positional?tolerance?of?the?pattern?of?holes，?there?is?no?generalized?discrimination?method?to?determine?whether?an?algorithm?construction?or?found?error?boundary?meets?the?condition?of?the?minimum?zone?or?not.?In?view?of?this?problem，?a?generalized?discrimination?method?for?the?minimum?zone?of?the?self-reference?positional?tolerance?of?the?pattern?of?holes?based?on?boundary?points?is?studied.?This?paper?analyzes?the?relative?spatial?relationship?between?the?measure?point?set?and?the?error?boundary?of?the?pattern?of?holes，?establishes?the?model?of?the?minimum?zone?of?the?positional?tolerance?of?the?pattern?of?holes，?analyzes?the?basic?mathematical?form?and?its?basic?inference?of?the?discriminant?logic?of?the?minimum?zone，?establishes?the?basic?motion?matrix?of?boundary?points，?transforms?the?discriminant?logic?problem?of?the?minimum?zone?into?an?equivalent?matrix-based?generalized?discrimination?method，?and?finally?uses?an?example?to?verify?the?proposed?generalized?discrimination?method?for?the?minimum?zone?of?the?self-reference?positional?tolerance?of?the?pattern?of?holes.

Key?Words：Discrimination?method;?Positional?tolerance;??Pattern?of?holes;??Self-reference;??Error?evaluation

孔系自參考位置度誤差是機(jī)械零部件的一項(xiàng)重要幾何誤差，通常用于保障以孔系安裝定位的零件的可裝配性及裝配精度，在相關(guān)標(biāo)準(zhǔn)中的嚴(yán)格評(píng)定方法是最小區(qū)域法[1-2]。幾何誤差最小區(qū)域的幾何判別條件比較復(fù)雜，國(guó)標(biāo)和ISO給出了給定方向上的兩條平行直線、兩個(gè)平行平面及圓柱的共計(jì)十余條幾何判別準(zhǔn)則，但并未列舉孔系位置度誤差的最小區(qū)域判別準(zhǔn)則。

為了減少形狀誤差的判別條件款項(xiàng)，丁喜波等和熊有倫從不同角度提出了基于幾何學(xué)的統(tǒng)一判別方法[3-5]，統(tǒng)一了各類(lèi)形狀誤差的判別，但具體操作和計(jì)算仍較復(fù)雜，因此，目前幾何誤差的最小區(qū)域判別方法大多與具體評(píng)定算法相關(guān)。Ameta?G、肖歡等利用T-MAP等方法構(gòu)造的變動(dòng)域凸包，可以借助計(jì)算幾何方法枚舉所有“頂點(diǎn)”的誤差區(qū)域并找出其中最小值，即判別方法為數(shù)值上的“區(qū)域最小”[6-7]，這類(lèi)方法能準(zhǔn)確判定最小區(qū)域，但不適合測(cè)點(diǎn)較多的情況。自適應(yīng)虛擬量規(guī)法、旋轉(zhuǎn)投影法等基于被測(cè)要素的幾何特性來(lái)構(gòu)造邊界并搜索大小更合適的包容邊界，直至滿(mǎn)足最小區(qū)域的幾何判別條件[8-9]。閔浩晨、李新、LUO?J、王生懷等分別利用牛頓法、二分法等傳統(tǒng)優(yōu)化方法和差分進(jìn)化算法、混合教與學(xué)算法等智能優(yōu)化算法進(jìn)行幾何誤差評(píng)定，這些優(yōu)化算法的判別方法通常為兩次迭代間步長(zhǎng)或函數(shù)值的變化較小[10-13]；當(dāng)出現(xiàn)爭(zhēng)議時(shí)，這類(lèi)方法仍需要采用幾何判別方法裁定。

綜上所述，在經(jīng)常需要處理大量測(cè)點(diǎn)數(shù)據(jù)的當(dāng)下，還缺乏一種一般化的、程式化的最小區(qū)域判別方法，以便在出現(xiàn)評(píng)定爭(zhēng)議時(shí)裁定算法是否找到了最小區(qū)域。本團(tuán)隊(duì)近期研究了若干類(lèi)型幾何誤差最小區(qū)域的一般化判別方法，通過(guò)分析邊界點(diǎn)與誤差區(qū)域之間的相對(duì)空間關(guān)系，建立邊界點(diǎn)的基本分析矩陣，嘗試解決了圓柱度、空間直線度誤差的一般化判別方法[14-15]。

孔系位置度誤差是機(jī)械零部件中典型、重要且比較復(fù)雜幾何誤差，為解決其最小區(qū)域判別問(wèn)題，本文研究其基于邊界點(diǎn)矩陣的一般化的、程式化的判別方法。分析了圓柱測(cè)點(diǎn)集與最小區(qū)域邊界之間的空間關(guān)系以及最小區(qū)域成立條件的數(shù)理邏輯形式，并利用邊界點(diǎn)集矩陣的性質(zhì)提出一種最小區(qū)域的一般化判別方法。最后，通過(guò)一個(gè)評(píng)定實(shí)例驗(yàn)證了提出的孔系位置度一般化判別方法。

1?孔系位置度包容區(qū)域模型

1.1?孔系測(cè)點(diǎn)集與包容區(qū)域的相對(duì)方位

孔系位置度誤差包容區(qū)域是保持理想方向、位置的若干直徑相同的圓（柱），且每個(gè)圓（柱）都包容著相應(yīng)的孔心；孔系位置度誤差值為構(gòu)造的最小圓（柱）的大小。如圖1所示，當(dāng)孔系中各孔的位置不由其它幾何要素定義時(shí)，各孔位置的參考關(guān)系完全由自身決定，這時(shí)，孔系位置度是自參考的位置度。孔系自參考位置度通常用于保障以孔系安裝定位的零部件的可裝配性及裝配精度。

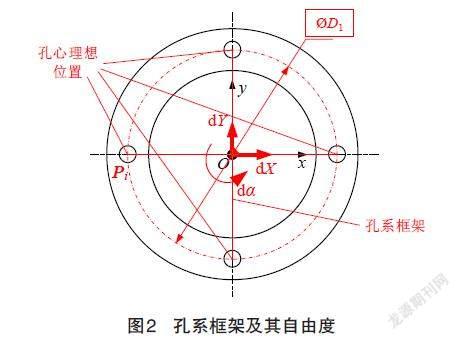
如圖2所示，構(gòu)造孔系自參考位置度包容區(qū)域時(shí)，可以先建立XOY平面坐標(biāo)系，在坐標(biāo)系上建立評(píng)定孔系位置度的孔系框架。對(duì)于孔系自參考位置度而言，孔系框架的幾何形狀是固定的，但方向、位置沒(méi)有外部參考物，因此，孔系框架是可以浮動(dòng)的，具有在XOY平面內(nèi)的兩個(gè)平移自由度dX、dY和繞原點(diǎn)的轉(zhuǎn)動(dòng)dα。理想孔心可以描述為被測(cè)孔心Pi的集合{Pi|Pi=（Xi，Yi），i=1，2，…}。

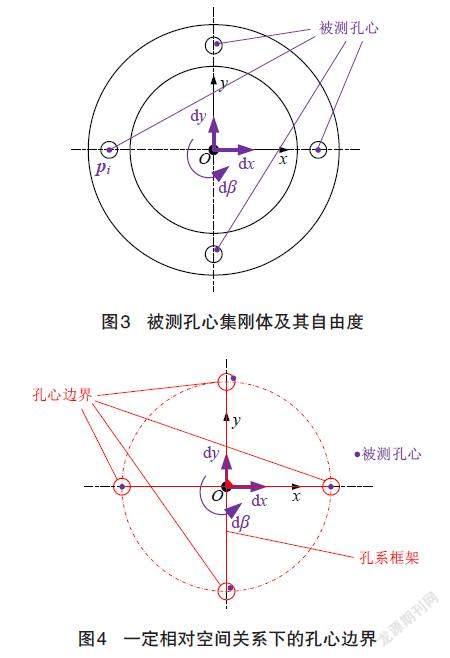
如圖3所示，作為零部件的組成部分，各被測(cè)孔心可以視為剛體上的若干固定點(diǎn)，它們之間的相對(duì)位置是固定的；因?yàn)樽詤⒖嘉恢枚裙钜?guī)范沒(méi)有直接定義測(cè)點(diǎn)與參考系之間的關(guān)系，所以被測(cè)孔心集剛體{pi|pi=（xi，yi），i=1，2，…}也可以相對(duì)于XOY平面、相對(duì)于孔系框架浮動(dòng)，被測(cè)孔心集剛體{pi}自由度方向?yàn)檠豿、y軸的平動(dòng)dx、dy和繞原點(diǎn)的轉(zhuǎn)動(dòng)dβ。

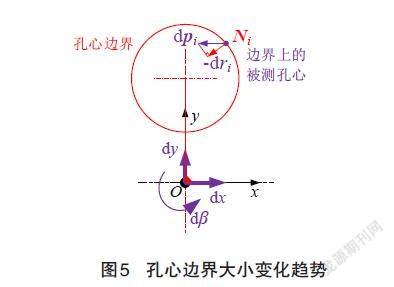
如圖4所示，孔系框架、被測(cè)孔心集剛體都是可以浮動(dòng)的，當(dāng)它們處于某個(gè)相對(duì)空間關(guān)系時(shí)，可以根據(jù)各被測(cè)孔心到孔系框架上相應(yīng)理想點(diǎn)的距離的最大值，作出相應(yīng)的孔心邊界。一定空間相對(duì)關(guān)系下，測(cè)點(diǎn)pi到孔系框架上相應(yīng)理想點(diǎn)Pi的距離為ri=|Pi-pi|，孔心邊界的半徑D=2max?ri。

孔系自參考位置度的值應(yīng)當(dāng)為孔系框架和被測(cè)孔心集剛體浮動(dòng)過(guò)程中孔心邊界直徑的最小值Dmin。顯然，取決于孔系框架和被測(cè)孔心集剛體之間的相對(duì)空間位置，兩者只需要保持一個(gè)運(yùn)動(dòng)、一個(gè)靜止即可。為便于分析計(jì)算，本文令孔系框架保持靜止，令被測(cè)孔心集剛體運(yùn)動(dòng)。

當(dāng)按自由度方向調(diào)整被測(cè)孔心集剛體時(shí)，被測(cè)孔心pi的方位變化趨勢(shì)dpi如公式（1）和圖3所示。

其中：Rdβ為測(cè)點(diǎn)繞原點(diǎn)O逆時(shí)針旋轉(zhuǎn)的坐標(biāo)變換矩陣，E2×2為單位矩陣；自由度調(diào)整量極小，因此sin?dβ≈dβ，cos?dβ≈1，dβ·dβ≈0。

1.2?孔心邊界的變化趨勢(shì)

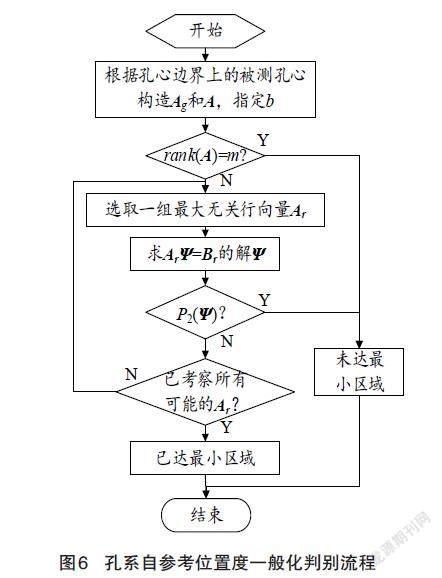
孔系框架和被測(cè)孔心集剛體有相對(duì)方位變化趨勢(shì)時(shí)，孔心邊界的大小變化趨勢(shì)僅受與孔心邊界接觸的被測(cè)孔心影響。如圖5所示，被測(cè)孔心pi到理想孔心Pi距離的變化趨勢(shì)dri，是dpi在孔心邊界法向Ni=[（Xi-xi）/ri，（Yi-yi）/ri]T上的投影，即dri=-dpi·Ni。將dpi表達(dá)式公式（1）代入投影公式，可以得到dri的代數(shù)表達(dá)式，如公式（2）所示：

為便于分析，可以將公式（2）中pi自由度運(yùn)動(dòng)趨勢(shì)合記為運(yùn)動(dòng)趨勢(shì)向量Ψ=[dx，dy，dβ]T，Ψ的系數(shù)合記為運(yùn)動(dòng)系數(shù)向量Ai，如公式（3）所示。

將Ai、Ψ代入公式（2），可以得到dri的線性向量表達(dá)式，如公式（4）所示。

記G={g}為與孔心邊界接觸的被測(cè)孔心序號(hào)集，則孔心邊界變化趨勢(shì)dR=min?drg。代入公式（4），可以得到dR的向量表達(dá)式，如公式（5）所示。

2?孔系自參考位置度最小區(qū)域的表達(dá)

2.1?2 孔系自參考位置度最小區(qū)域的邏輯形式

孔系自參考位置度的最小區(qū)域可以一般性地描述為：被測(cè)孔心剛體與孔系框架間的相對(duì)方位已調(diào)整至最佳，相對(duì)方位發(fā)生任意改變時(shí)，在孔心邊界上至少存在一個(gè)被測(cè)孔心使孔心邊界不會(huì)更小。據(jù)此可以建立最小區(qū)域判別的基本邏輯形式，如公式（6）所示，其中，h∈G。

公式（6）是對(duì)于運(yùn)動(dòng)趨勢(shì)向量Ψ的“求證”形式，不便于直接分析其是否成立。其互斥的否命題形式如公式（7）所示，是對(duì)于運(yùn)動(dòng)趨勢(shì)向量Ψ的“求解”形式，有利于進(jìn)行下一步數(shù)學(xué)分析。因此，本文建立基于公式（7）的最小區(qū)域判別：如果公式（7）成立，則孔心邊界不是最小區(qū)域，否則，孔心邊界是最小區(qū)域。

記A=[…，AgT，…]T為孔心邊界上被測(cè)孔心集的運(yùn)動(dòng)系數(shù)矩陣，b=[…，drg，…]T為運(yùn)動(dòng)常數(shù)項(xiàng)，則公式（7）等價(jià)于公式（8）。

2.2?基于邏輯表達(dá)式的一般化判別方法

設(shè)孔心邊界上被測(cè)孔心數(shù)目為m，rank（A）=r，則Ag共有m個(gè)，A共有m行。當(dāng)rank（[A，b]）=rank（A）=r時(shí)，AΨ=b總是有解，即，公式（8）總是成立，孔心邊界不是最小區(qū)域。下面討論rank（[A，b]）>r時(shí)公式（8）的成立條件。

記B=[…，b，…]T，則公式（7）中的不等式組{AgΨ<b}在任意給定超平面AΨ=B上的基本解集Fj={Ψ}j不超過(guò)Cmr個(gè)，相關(guān)定義如下：

定義1：在AΨ=B中任選r個(gè)線性無(wú)關(guān)的運(yùn)動(dòng)系數(shù)向量Ag、對(duì)應(yīng)的drg及常數(shù)項(xiàng)b，分別集合成矩陣Ar、常數(shù)項(xiàng)br及常數(shù)項(xiàng)Br；線性方程組ArΨ=Br的解集Fj={Ψ}j就是不等式組{Au，vΨ<b}在超平面AΨ=B上的一個(gè)基本解集；其余的運(yùn)動(dòng)系數(shù)向量Ag及對(duì)應(yīng)的drg分別集合成矩陣As和常數(shù)項(xiàng)bs，s∪r=G。

由公式（11）可知，可以先求解方程ArΨ=Br的一個(gè)解Ψ，然后考察Ψ是否滿(mǎn)足P2（Ψ），即可判斷相應(yīng)的基本解集Fj={Ψ}是否為有效基本解集。

如果Ψ滿(mǎn)足P2（Ψ），則公式（8）成立，即公式（7）成立，孔心邊界并非最小區(qū)域；如果Cmr個(gè)ArΨ=Br的特解Ψ都不滿(mǎn)足P2（Ψ），則Cmr個(gè)ArΨ=Br的任意解Ψ都不滿(mǎn)足P2（Ψ），則公式（8）恒不成立，即公式（7）不成立而公式（6）成立，孔心邊界是最小區(qū)域。

綜上所述，孔系自參考位置度的最小區(qū)域統(tǒng)一判別方法的基本流程如圖6所示。

3?實(shí)例驗(yàn)證

本節(jié)以仿真法蘭盤(pán)的一組測(cè)點(diǎn)數(shù)據(jù)為對(duì)象，用優(yōu)化法評(píng)定仿真孔系的自參考位置度，并用本文提出的方法辨別優(yōu)化法是否準(zhǔn)確構(gòu)建了自參考位置度的最小區(qū)域，以驗(yàn)證提出的判定方法。

3.1?仿真法蘭盤(pán)的自參考位置度評(píng)定

本例根據(jù)法蘭盤(pán)孔系公差規(guī)范（圖7）用Matlab對(duì)法蘭盤(pán)孔系進(jìn)行仿真，每個(gè)孔16個(gè)仿真點(diǎn)，如圖8所示；測(cè)點(diǎn)原始數(shù)據(jù)可以通過(guò)編輯部或作者免費(fèi)咨詢(xún)獲取。

擬合得到8個(gè)孔的仿真中心pi后，可以用優(yōu)化法求解孔系自參考位置度，如公式（12）所示；優(yōu)化求解方法為Matlab?R2021a自帶的fminucon函數(shù)。

在MATLAB?R2014a中，自編程序求解得到仿真法蘭盤(pán)的自參考位置度為0.045mm，構(gòu)成與最小區(qū)域邊界接觸的仿真孔心的序號(hào)為1、3、5、6，如表1所示。

3.2?評(píng)定結(jié)果的判別

基于提出的判別方法，對(duì)表1中的評(píng)定結(jié)果進(jìn)行判別，判斷優(yōu)化法是否滿(mǎn)足最小區(qū)域條件。將位于孔心邊界上的仿真孔心的最終位置代入公式（3），可以求出運(yùn)動(dòng)系數(shù)向量Ai及運(yùn)動(dòng)系數(shù)矩陣A，如公式（14）所示。

指定m=4個(gè)b=-1，并將其集合為b=[b，b，b，b]T=[-1，-1，-1，-1]T。因?yàn)閞ank（[A，b]）=4>rank（A）=3，所以需要選取不超過(guò)Cmr=C43=4個(gè)Ar并檢驗(yàn)基本解的有效性。本例借助MATLAB?2014R內(nèi)置函數(shù)“nchoosek”在A的4個(gè)行向量中選取3個(gè)行向量。

以第一組為例，選取A的前3行為Ar，并將第4行向量視為As；選取Br=[b，b，b]T=[-1，-1，-1]T。用Matlab?2014R內(nèi)置函數(shù)“＼”求得ArΨ=Br的解Ψ。因?yàn)锳4Ψ=-0.0993>-1，P2（Ψ）不成立，所以基本解集（單元素集）F1=Ψ*并不是有效基本解集。

依次檢驗(yàn)4組Ar對(duì)應(yīng)的基本解集，發(fā)現(xiàn)并不存在有效基本解集。因此，優(yōu)化法求得的位置度孔心邊界滿(mǎn)足最小區(qū)域條件，孔系的自參考位置度誤差為0.045mm。

4?結(jié)語(yǔ)

分析了孔系被測(cè)孔心集剛體與孔心框架之間的相對(duì)空間關(guān)系；基于數(shù)理邏輯、線性方程組和不等式組理論，分析了孔系自參考位置度誤差的最小區(qū)域的判別條件，并給出了相關(guān)線性矩陣及流程圖。提出的判別方法由程式化的運(yùn)算、條件選擇構(gòu)成，是一種程式化的、一般化的代數(shù)判別方法，可以在出現(xiàn)評(píng)定爭(zhēng)議時(shí)裁定算法是否找到了最小區(qū)域。

用優(yōu)化法評(píng)定了一個(gè)仿真法蘭盤(pán)的孔系自參考位置度誤差，用提出的方法檢驗(yàn)了優(yōu)化法的評(píng)定結(jié)果。提出的判別方法識(shí)別了優(yōu)化法求得的最小區(qū)域，具備最小區(qū)域判別的能力。

該文推導(dǎo)了孔系自參考位置度誤差最小區(qū)域的一般化判別方法，其中運(yùn)用的自由度、法向量、數(shù)理邏輯、線性理論等也適合其他形狀的最小區(qū)域評(píng)定。未來(lái)可以參考該文方法繼續(xù)研究輪廓度等形狀、方向和位置誤差的最小區(qū)域判定。

參考文獻(xiàn)

• AMETA?G，SINGH?G，DAVIDSON?JK，?et?al.Application?of?T-MAPS?for?Composite&nbsp;Position?Tolerance?for?Patterns?of?Features[C].ASME?International?Design?Engineering?Technical?Conferences/Computers?and?Information?in?Engineering?Conference（IDETC/CIE?2017），2017，1：V001T02A014.