一維慢速烤燃模型點火點位置及其溫度的理論計算

張坤, 智小琦, 肖游, 王帥

(1.中北大學 機電工程學院, 山西 太原 030051;2.中國兵器裝備集團自動化研究所有限公司 智能制造事業部, 四川 綿陽 621000;3.湖北航天化學技術研究所 航天化學動力技術重點實驗室, 湖北 襄陽 441003)

0 引言

研究彈藥在熱環境中的響應特性對彈藥在壽命期的安全使用具有重要意義。因為彈藥無論是受熱刺激、強電磁輻射或二者的綜合作用,最終導致彈藥響應的均是因含能材料受熱后的自持反應所致。目前,模擬彈藥受熱刺激作用的研究方法主要是快速烤燃和慢速烤燃。快速烤燃模擬彈藥在大火作用下的響應特性,慢速烤燃模擬彈藥在暗火作用下的響應特性。研究手段主要采用試驗和仿真技術。試驗方法主要采用北大西洋公約組織標準化協定STANAG 4240(快速烤燃試驗)和STANAG 4382(慢速烤燃試驗),試驗研究內容包括彈藥尺寸[1-2]、約束條件[3-4]、裝藥密度及間隙[5-6]、含能材料配方[7]、熔鑄炸藥點火機理[8]以及緩釋結構特性[9]等對彈藥響應溫度、響應烈度的影響研究,已達到既深又廣的程度;仿真研究與試驗研究既相輔相成又互相補存和促進,能獲得點火時刻的溫度及其梯度、點火點位置、點火前壓力[10]、內部機理的分析[11-12]及點火后的瞬時響應特性[13]等內容。其中關于點火后的含能材料自持反應特性的仿真研究軟件,目前只有美國ALE3D軟件和Uintah軟件。

從上述情況可見,研究彈藥的熱刺激,無論從試驗還是仿真都取得了很大的成就。但是關于純理論研究點火點位置和點火溫度的文章,目前鮮有報道,而理論研究是彈藥熱刺激研究不可或缺的內容,是對熱爆炸理論的完善和補存,具有重要的意義。本文擬采用疊加原理和分離變量方法,首次將炸藥非反應性熱傳導與自熱反應熱傳導拆分,以一維炸藥模型為基礎,研究慢速烤燃的溫度分布及點火點位置的解析解,分析點火點位置的一維變化規律,以期為烤燃研究奠定理論基礎。

1 一維數學理論模型

1.1 理論推演的假設

為簡化理論計算,需對炸藥的烤燃過程作如下假設:

1)炸藥為凝聚炸藥,炸藥在加熱過程中不發生相變;

2)彈體外壁均勻升溫,升溫速率為固定值;

3)忽略殼體與炸藥間的接觸熱阻;

4)炸藥的熱導率、比熱容、密度均為恒值;

5)炸藥活化能、指前因子、反應熱均為常數;

6)炸藥按照零階動力學定律分解。

1.2 慢速烤燃一維模型

炸藥的熱傳導方程用式(1)[14]描述:

(1)

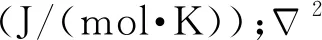
(2)

當則炸藥厚度L=2δ,其中δ為厚度值的一半。則一維無限平板模型的熱傳導可用式(3)來描述:

(3)

式中:α為熱擴散系數,且α=λ/ρc;S(x,t)為熱傳導方程的源項,用式(4)表示:

(4)

式(3)的定解條件如下:

1)初始條件:T(x,0)=Tr,其中Tr為初始溫度;

2)邊界條件:T(±δ,t)=κt+Tr,其中κ為升溫速率。

2 求解

2.1 溫度場的拆分

當沒有化學反應時,炸藥熱傳導問題的解析解即非反應性熱傳導比較容易求解。但是,具有化學反應的熱傳導方程即反應性熱傳導是極難獲得解析解的。為進一步求解熱傳導方程式(3),需要用到疊加原理[15],將原問題T(x,t)分解為非反應性熱傳導項Tt(x,t)和自熱反應熱傳導項Ts(x,t)兩個子問題。其中非反應熱傳導式為

(5)

式(5)相應的定解條件如下:

1)初始條件:Tt(x,0)=Tr;

2)邊界條件:Tt(±δ,t)=κt+Tr。

自熱反應熱傳導的方程如下:

(6)

式(6)的定解條件如下:

1)初始條件:Ts(x,0)=0;

2)邊界條件:Ts(±δ,t)=0。

則原方程(式(3))的解T(x,t)可通過T(x,t)=Tt(x,t)+Ts(x,t)求得。

2.2 非反應性熱傳導問題的求解

式(5)的熱傳導子問題不包含自熱源項,即屬于沒有化學反應的惰性情況下的熱傳導問題。由于變量x、t相互獨立,使用分離變量法[16]將Tt(x,t)寫為

Tt(x,t)=X(x)U(t)

(7)

式中:X(x)為位置x的函數;U(t)為時間t的函數。

將式(7)代入式(5),有如下等式:

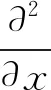
(8)

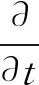
(9)

式中:k為常數。

式(8)根據邊界條件Tt(±δ,t)=κt+Tr,通過Strum-Liouville理論求解有

Xn(x)=Cnsin[nπ(-x+δ)/(2δ)]

(10)

式中:Cn為常數,X0(x)=C0;固有值λn=nπ,n=0,1,2,3,…。

對式(9)求解,有

Un(t)=Bne(-απ2n2t)/4δ2

(11)

式中:Bn為常數。

則非反應性熱傳導方程式(5)的通解為

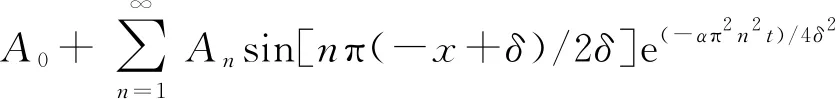
(12)

式中:An為常數,且對于Tt(x,t)解函數首項Tt0(x,t)有Tt0(x,t)=A0。

代入初始條件Tt(x,0)=Tr,進一步求得非反應性熱傳導方程的精確解Tt(x,t)為

(13)

隨著時間t的不斷增加,無窮級數項將逐漸減小,非反應性熱傳導所產生的溫度分布將逐漸穩定。其中初始溫度Tr作為常數項,不影響非反應性熱傳導所產生的溫度分布。

2.3 自熱反應熱傳導問題的求解

對于式(6)的自熱反應熱傳導問題,非齊次項(即源項)為Arrhenius方程,直接求解是相當復雜的。通過進一步將源項S(x,t)泰勒展開:

(14)

當自熱反應產生的溫度Ts小于非反應性熱傳導溫度Tt的1%時,源項S(x,t)可取泰勒展開式首項近似代替,作近似后的自熱反應熱傳導方程如下:

(15)

式中:

(16)

對于式(15)的求解,采用分離變量法[17]。將Ts(x,t)、S(x,t)分別按固有函數展開為Dn(t)、Sn(t),于是有

(17)

式中:

(18)

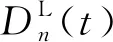
(19)

再將其反變換后,則有

(20)

這樣,可解得自熱反應熱傳導方程的解Ts(x,t)為

Ts(x,t)=

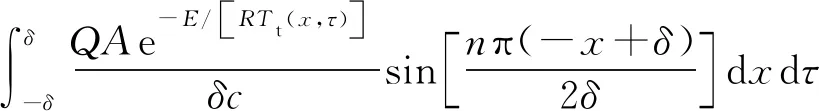
(21)

觀察解的結構,不難發現式(21)中Ts(x,t)包含Arrhenius溫度積分,直接求出其精確的結果極其困難[18]。但Ts(x,t)中常數顯然不影響對其最高溫度所在位置的求解,即指數前因子A、反應熱Q不影響自熱反應熱傳導溫度最高值所在位置,進而不影響炸藥在烤燃中的點火點位置。隨著升溫速率κ的增加,炸藥兩側升溫加快,則點火點位置向邊界移動。

3 慢速烤燃試驗

3.1 試驗設計

設計尺寸為φ75 mm×295 mm烤燃彈,殼體材料選用45號鋼,兩端帶螺紋的端蓋連接,端蓋和殼體壁厚均為5 mm。內部裝藥為甘肅銀光化學工業集團有限公司生產的RDX炸藥,單節藥柱直徑為57.4 mm,長度為47.5 mm,共6節,藥柱總長285 mm,長徑比為5,裝藥密度為1 610 kg/m-3。

為獲得烤燃試驗過程中,炸藥內部的溫度的變化情況,在每節藥柱中間刻槽埋入φ1 mm的上海自動化儀表股份有限公司生產的WRNK191型鎧裝電偶(精度為0.1 K,熱響應時間≦3 s)。藥柱與藥柱之間以及藥柱與熱電偶之間均采用蟲膠漆粘接固定。熱電偶的溫度測點由上至下編號1～5號,兩相鄰測點及邊緣測點至端面的間距均為47.5 mm,溫度測點位置如圖1所示。由于采用等長壓制藥柱試驗,無法獲得其他位置的溫度情況。

圖1 溫度測點的位置示意圖Fig.1 Location of temperature measuring points

試驗彈試驗前狀態如圖2所示。試驗采用圓柱形保溫箱進行加熱,試驗裝置如圖3所示。

圖2 試驗彈體Fig.2 Tested ammunition

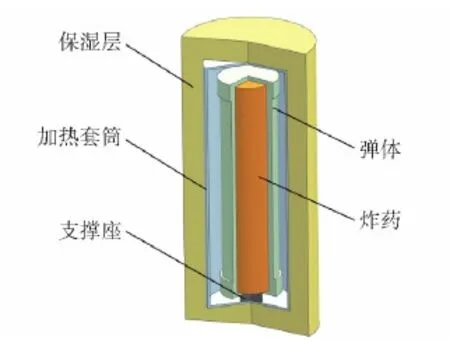
圖3 慢速烤燃試驗裝置Fig.3 Slow-cook test setup

使用日本島電公司生產的MR13溫控儀對烤燃彈外壁進行升溫控制,并使用美國Fluke公司的1586A多路測溫儀采集各測點的溫度數據,采樣周期為1 s。從室溫305 K開始,以3.3 ℃/h的固定速率升溫,直至烤燃彈發生響應。

3.2 試驗結果

試驗藥柱中5支熱電偶和外壁1支熱電偶在點火時刻的測量結果如表1所示,試驗中各測點溫度變化曲線如圖4所示。由于炸藥內部的自熱反應隨溫度的升高而逐漸加劇,臨近響應時,各測點的溫度迅速升高。從5條測溫曲線可見,藥柱的兩側1號和5號熱電偶測得的溫度最高,3號點測得的溫度最低,可見點火區域位于藥柱兩側,點火時外壁溫度為468.9 K。

表1 點火時刻熱電偶的測量結果

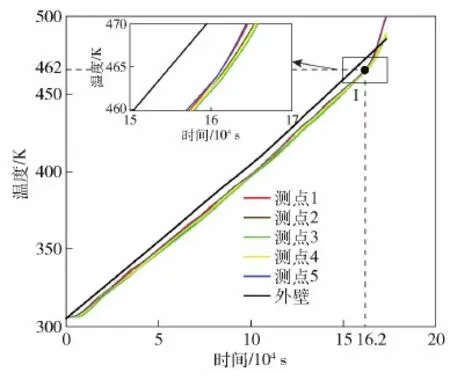
圖4 溫度變化曲線Fig.4 Temperature history curves

烤燃彈響應后,試驗點產生較深的彈坑,加熱套筒與烤燃彈殼體完全碎裂。由于試驗在野外溝壑中進行,響應后僅回收到少部分碎片,如圖5所示。根據響聲及以往同種炸藥的烤燃試驗情況,綜合判斷烤燃彈的響應等級為爆轟。

圖5 試驗結果Fig.5 Test results

4 算例及驗證

4.1 檢驗理論與試驗的一致性

為檢驗理論與試驗的一致性,以試驗藥柱為例,利用表2中的物性參數和動力學參數,對式(21)的解析解進行計算。

表2 RDX炸藥物性參數和動力學參數

對于任意長圓柱,單從徑向或軸向考慮,傳熱均屬于一維問題,僅考慮徑向傳熱時,因溫度沿縱軸均勻分布,沒有區別。而單考慮軸向傳熱時,因溫度分布不均勻,能體現出位置的差別。同理,僅考慮自熱兩個方向也均屬于一維問題,故對藥柱軸向的溫度分布進行計算[19]。

已知炸藥厚度 、初始溫度為305 K、升溫速率κ=3.3 ℃/h。使用Maple數學軟件[20]和Clenshaw-Curtis正交方法[21]求解,控制無窮級數的舍入誤差不大于0.1%。理論解的藥柱沿軸線方向的部分溫度值如表3所示。

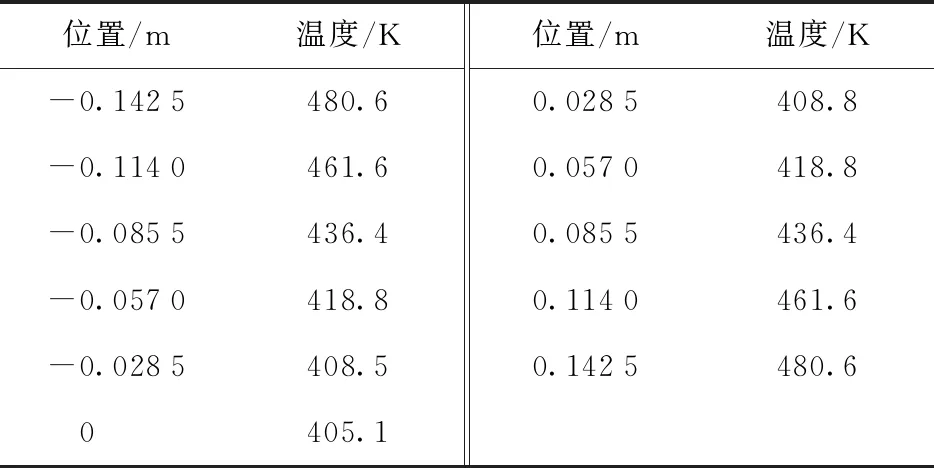
表3 沿軸線方向的溫度值

外壁溫度為484.6 K時,理論解與測點測量值的溫度分布如圖6所示。各測點測量得到的溫度分布趨勢與理論解的溫度分布趨勢相符,但是由于試驗值是三維結果,而理論僅是一維結果,因此兩曲線的彎曲程度有所不同(即對于試驗藥柱,沿軸向的傳熱屬于一維問題[19])。

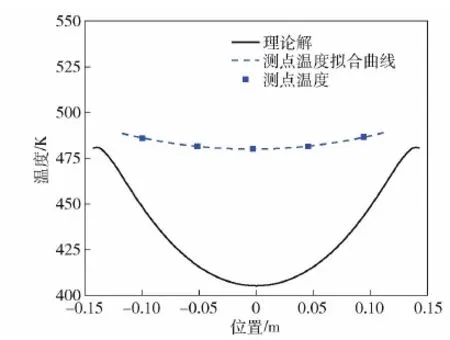
圖6 溫度分布Fig.6 Temperature distribution

為直觀地比較理論解的相對溫度分布與試驗測得的相對溫度分布,將圖6中試驗測得的溫度值、理論解中截取與試驗測量范圍(-0.095～0.095 m)對應區間的溫度值,再根據各自的溫度幅值分別作如下歸一化處理:

(22)

式中:xN為歸一化后的溫度值;xi為歸一化前的溫度值;xmax為歸一化前數據中的最高溫度值;xmin為歸一化前數據中的最低溫度值。通過歸一化將試驗測得的溫度值、理論解與試驗對應位置的溫度值映射到0～1之間,得到各個位置的相對溫度分布,如圖7所示。理論解各個位置的溫度之間的比例與試驗結果一致,即理論解的相對溫度分布與試驗測得的相對溫度分布相符,進一步驗證了理論解的溫度分布的正確性。

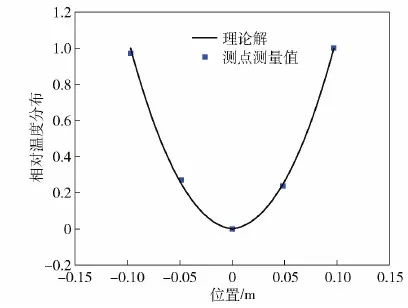
圖7 相對溫度分布Fig.7 Relative temperature distribution

4.2 數值驗證

為進一步驗證理論解的正確性,使用數值方法對解析解式(21)進行驗證。Suceka[22]對熱傳導方程式(1)進行了有限差分近似。對于無限大平板而言,關于位置x的偏導數可以通過以下差分來近似:

(23)

式中:Δx為將厚度為L的炸藥被均勻分為n份后的寬度;上下標用于區分網格對應的時間和位置,上標j為時間序列,下標i為位置序列。

對時間t的偏導數進行同樣的有限差分近似:

(24)

式中:Δt為時間增量。

使用有限差分替代熱傳導方程式(1)中的偏導數,即得到炸藥熱傳導離散方程:

(25)

同理,建立非反應性熱傳導離散方程如下:

(26)

對于式(25)與式(26)具有相同定解的條件如下:

通過式(25)可以獲得任意時刻炸藥內部的溫度分布;將式(25)與式(26)同時刻的溫度結果作差,即可獲得該時刻炸藥自熱反應熱傳導的溫度分布。

以上兩種顯式方法的穩定性由空間步長和時間步長的比值決定。對于熱傳導方程,如果滿足以下穩定條件[23],則該方法是穩定的:

(27)

穩定性條件保證了有限差分解的穩定性,該條件僅在炸藥分解緩慢的情況下,能保證解的精確性。對于慢速烤燃,點火時自熱反應產生的熱量很低,故適用于該判據。

計算選取RDX炸藥為研究對象,計算中使用的物性參數和動力學參數的值如表2所示,炸藥厚度、初始溫度Tr為305 K、升溫速率κ=3.3 ℃/h。代入以上參數,對熱傳導離散方程式(25)、熱傳導離散方程式(26)賦予初始條件與邊界條件,以時間增量Δt=1 s循環迭代離散方程(即j+1時刻的溫度分布由j時刻的溫度分布計算得出),并將各個時刻的溫度分布進行輸出。

點火點的溫度變化如圖8所示。在D點(加熱時間約為177 000 s時)發生點火,自熱反應逐漸加劇,溫度不再可控,進而發生響應。

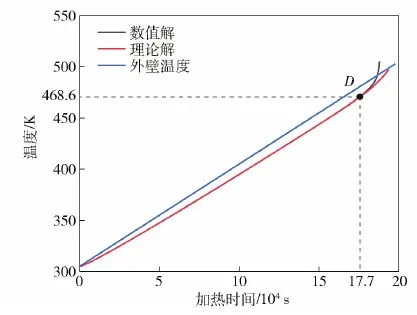
圖8 點火點溫度的理論解與數值解Fig.8 Theoretical and numerical results of the temperature of ignition point

炸藥點火溫度的理論計算結果與采用文獻[22]方法的數值解具有良好的匹配度,理論計算值為468.8 K;數值計算值為468.6 K,誤差不超過1%。

點火時刻(外壁溫度為480.7 K時),炸藥總體溫度(即非反應性熱傳導溫度與自熱反應熱傳導溫度之和)分布與僅自熱反應所產生的溫度分布如 圖9 所示,點火點位置位于炸藥兩側,與試驗結果相符。總體溫度分布主要受升溫邊界的影響,由于點火前達到分解能壘的分子數很少,自熱反應所產生的溫度較低。自熱反應所產生的溫度的理論計算結果與數值解相比,最大誤差為8.8%(誤差主要來自于式(14)對源項的近似處理);自熱反應溫度最高值所在位置的計算結果與數值解相比,最大誤差不超過1%。

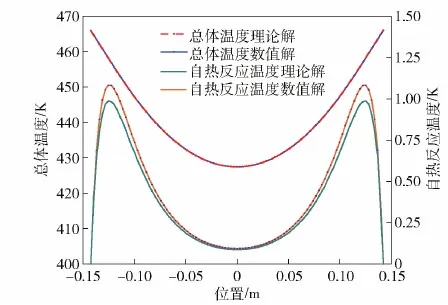
圖9 炸藥厚度L=0.285 m時的理論計算結果與數值計算結果Fig.9 Theoretical and numerical results with explosive thickness L=0.285 m

5 結果與討論

自熱反應溫度最高值的位置是由炸藥自熱反應與邊界的熱散失共同作用的結果。圖10為不同厚度條件下,炸藥自熱反應溫度最高值隨時間的變化情況。由圖10可見,隨著時間的增加,自熱反應溫度最高值所在的相對位置(即|x/δ|)將趨于穩定,直至發生點火。

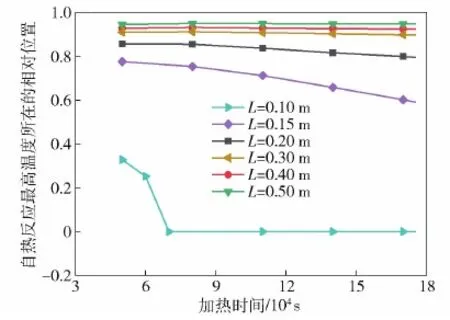
圖10 不同厚度炸藥自熱反應溫度最高值所在的相對位置Fig.10 Relative location of the maximum value point of self-heating reaction temperature of explosiveswith different thicknesses

在炸藥厚度較薄的情況下,自熱反應溫度最高位置將迅速移動至中心;隨著炸藥厚度L的增加,位置移動的相對量逐漸減小,當炸藥厚度L>0.3 m時,從50 000 s直至發生點火,自熱反應溫度最高位置的相對移動量不大于2%。顯然可以認為在烤燃試驗進行到一定時間之后,溫度相對分布趨于穩定,自熱反應溫度最高值位置隨時間不再發生改變,直至點火。這樣,可以通過理論計算,預則最高溫度及其所在位置,為降低響應等級的結構設計提供便利。

點火時,自熱反應溫度最高值所在位置至邊界的距離變化如圖11所示。當炸藥厚度L>0.3 m時,隨著炸藥厚度的進一步增加,自熱反應溫度最高值所在位置至邊界的距離變化不大于2%,且最高值所在位置至邊界的距離逐漸趨于穩定。即隨著炸藥厚度的增加,邊界的熱散失條件逐漸成為影響點火點位置的重要因素。

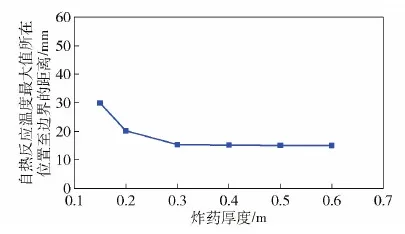
圖11 自熱反應溫度最高值所在位置至邊界的距離Fig.11 Distance from the maximum value point of self-heating reaction temperature to boundary

當炸藥厚度L>0.3 m時,從邊界至中心的自熱反應溫度梯度如圖12所示,隨著炸藥厚度的增加,點火點附近的自熱反應溫度梯度趨于恒定。隨著炸藥厚度的增加,自熱反應溫度分布的規律相似。

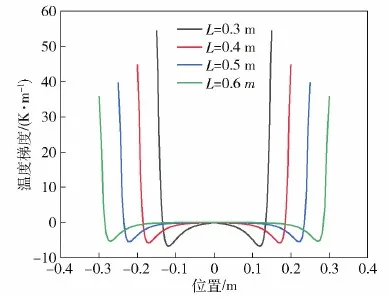
圖12 炸藥邊界到中心的自熱反應溫度梯度Fig.12 Temperature gradient of self-heating reaction from boundary to center of explosives

6 結論

本文通過理論解析的方法研究一維凝聚炸藥慢速烤燃的點火點位置及點火溫度。得出以下主要結論:

1)將炸藥非反應性熱傳導與反應性熱傳導拆分,通過理論方程及計算可得出慢烤條件下一維凝聚炸藥內部的溫度分布情況及點火點位置,并與試驗及數值計算結果進行對比,驗證了理論方程及計算的正確性。

2)通過理論計算可得到一維炸藥點火時刻僅自熱反應所產生的溫度分布和自熱反應溫度最高值所在位置;獲得點火時刻一維凝聚炸藥溫度最高值所在位置及溫度梯度沿厚度的變化規律。為烤燃試驗點火溫度及位置的預測提供了可靠的理論依據。