循環加載下復合推進劑的非線性熱粘彈性本構模型①

童 心,許進升,李 博

(1.中國船舶科學研究中心,無錫 214082;2.南京理工大學 機械工程學院,南京 210094)

0 引言

以固體火箭發動機為動力的空空導彈在完整的壽命期內一般要經歷運輸、貯存、掛飛、機動飛行和自主飛行等階段,在長途運輸以及掛機飛行過程中的振動頻率高達幾千赫茲,作為導彈動力裝置的固體火箭發動機也隨之產生高頻振動,發動機內的復合推進劑藥柱隨著振動載荷的作用會發生疲勞熱耗散,導致的溫度驟升和熱軟化效應對發動機的安全性有著顯著影響。

由于粘合劑大分子間的纏結、相互吸引以及化學作用,再加上粘合劑分子與填充顆粒間的物理和化學吸附,復合推進劑內部形成了多尺度、多相互作用的多網絡結構,力學行為可用非線性粘彈性理論來進行描述。PARK等[1]建立了含損傷熱粘彈性本構模型,利用折算時間將不同溫度下的材料函數統一至參考溫度下,隨后HA等[2]將模型拓展為三維形式,HINTERHOELZL等[3]完整地提出了相關的數值算法,將其應用于有限元軟件Abaqus,成功地模擬了端羥基聚丁二烯(HTPB)推進劑在單軸和多軸復雜應力條件下的力學響應。張永敬等[4]通過HTPB推進劑蠕變回復實驗來擬合了Schapery非線性本構模型的參數,通過與線性粘彈性本構計算的結果和實驗數據對比,證明了Schapery非線性本構模型能夠很好反映復合推進劑的力學響應。

復合推進劑作為一種溫度敏感的顆粒填充類聚合物,其力學表現受到變形中能量耗散的影響,能量耗散的宏觀表現是變形過程中自身溫度上升[5]。然而,目前大多數非線性粘彈性本構模型的研究仍集中于單純力學狀態的解釋與預測,對變形過程中的能量耗散及其影響則關注較少。在高應變率、交變加載等動態條件下,熱交換的特征時間比載荷作用時間大幾個數量級,由機械功轉化而來的熱能帶來較大的溫升,因而材料因變形而生熱的性質(自熱效應)不容忽視,在這些情況下必須考慮力學耗散引起的熱源。由于復合推進劑特殊的組成與結構,這種自熱現象在高應變率沖擊加載和高頻率循環加載下尤為顯著。在熱力學框架下,材料的時效變形行為本質上是一種非平衡演化過程,在熱力學理論框架下建立的本構模型與守恒定律相一致,具有嚴格的熱力學背景和理論基礎,不僅滿足熱力學基本定律,還能表征材料內部的不可逆能量耗散過程和材料的熱力學狀態、性質[6-8],對熱力耦合狀態有直觀的描述[9]。RODAS等[10]提出了適用于丁苯橡膠有限變形的非線性粘彈性本構模型,以不可逆熱力學內變量理論為基礎,引入了Helmholtz自由能,并構建了內變量的演化方程,很好地模擬了丁苯橡膠低周疲勞的生熱現象。KRAIRI等[11]將總應變分解為粘彈性應變、熱應變和粘塑性應變,結合時溫等效原理,在不可逆熱力學框架下將MILED等[12]的粘彈-粘塑性等溫本構模型拓展為非等溫形式,發展了熱粘彈-粘塑性本構模型,并在熱塑性聚合物的有限元仿真中進行了完全耦合形式的熱力分析。SHEN等[13]進行了類似工作,模型為熱彈-粘塑性本構模型。目前,關于復合推進劑循環加載下的自熱效應未見相關報道。

為了精確描述復合推進劑循環加載下的熱力耦合特性,本文基于不可逆熱力學理論建立了適用于復合推進劑的非線性熱粘彈性本構模型,并通過實驗驗證了模型和數值算法的正確性,本構模型成功表征了復合推進劑在不同加載模式下的非線性力學行為和自熱效應,為高能固體聚合物的熱力學表征提供參考。

1 本構模型的構建

1.1 非線性熱粘彈性本構模型

高分子聚合物材料的力學行為通常具有高度的時間和環境依賴性。Schapery基于不可逆熱力學原理,通過引入應力或應變相關標量,使粘彈性模型非線性化,并滿足熱力學基本定律。因此,該模型也被稱為熱力學本構模型。在Schapery模型的基礎上,提出以下非線性熱粘彈性本構模型：

(1)

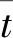
(2a)

(2b)

式中aT為時間-溫度等效因子;am為時間-濕度等效因子;aa為時間-老化等效因子。

若濕度等環境因素保持恒定,可認為am=aa=1。本文認為復合推進劑屬于各向同性的均質材料,滿足連續介質力學的基本假設,因此有

Cve(t,σ)=2G(t,σ)Idev+3K(t,σ)Ivol

(3)

其中,Idev為四階偏斜張量;Ivol為四階體積張量;G(t,σ)和K(t,σ)分別為剪切模量和體積模量,具有Prony級數的形式：

(4)

本構模型的關鍵是選擇合適的非線性粘彈性應力函數g1(σ)和g2(σ),它們是構成模型的非線性元素。HAJ-ALI等[14]曾采用多項式形式的應力函數,該函數雖考慮了應力的影響,但函數的參數繁多,難以準確獲取。此外,MULIANA等[15]也提出了具有指數形式的非線性函數,但他們所提出的本構模型未應用于循環加載實驗。此外,這些模型中函數參數對最終結果的影響不明確。為了克服上述不足,提出具有指數函數形式的非線性應力函數：

(5)

其中,k1、m1、k2、m2和C2為待求參數;σ0為線性粘彈性極限應力,是區分線性粘彈性與非線性粘彈性應力的臨界值;σvM為von Mises等效應力,其表達式為

(6)

(7)

綜上可知,g1(σ)和g2(σ)是關于應力歷史的函數,也是關于時間t的函數。

1.2 產熱方程

材料的循環屬于不可逆的熱力學過程,伴隨著能量的耗散,并導致材料自身溫度場發生變化。為了描述材料的熱力耦合特性,需要建立能量平衡方程。一般情形下,Clausius-Duhem不等式為

(8)

式中q為熱流矢量;ψ為Helmholtz自由能;S為熵;T為溫度;φ為能量耗散率;φmec為由于外部機械載荷引起的能量耗散率;φT為熱耗散率。

結合熱力學第一定律可得到：

(9)

因此,產熱方程為

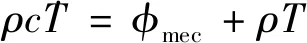
(10)

式中 ?包括熱彈性源與內耦合源;φmec為固有耗散轉化為熱能,即自熱效應。

自熱效應在高速沖擊和高頻循環載荷下具有重要的意義。若?和φmec均為0,式(10)變為非熱力耦合的溫度平衡方程,即溫度場不受材料本構關系的影響。根據Fourier定律,熱流矢量表示為

q=-κ·T

(11)

式中κ為導熱張量,若導熱是各向同性的,則κ=κl,κ為熱導率。

在無外部熱源的情況下,rext=0,式(3)變為

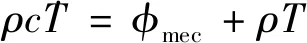
(12)

式(12)表明,在無外部熱源作用時,材料在循環過程中的溫度變化主要受熱彈性響應、非彈性響應和熱傳遞(熱傳導、與環境的熱對流及熱輻射)三方面的影響。與非彈性耗散源相比,熱彈性效應對試件表面溫度變化的影響很有限,僅僅引起溫度的微小波動;對處于粘彈性變形的復合推進劑而言,內部結構改變不涉及相變,因而內耦合源也可以忽略[16]。

綜上所述,在關于復合推進劑能量耗散的分析中,可認為?≈0。

1.3 能量耗散

線性熱粘彈性本構模型能量耗散φtve的表達式為

φmec=φtve

(13)

其中,φ和m均為松弛函數,反映了溫度因素的影響。若溫度的變化幅度不大,材料力學特性受溫度變化的影響較小,可假設φ和m均為0,則有

(14)

該式與等溫條件下線性粘彈性本構模型推導的能量耗散表達式相似,因而：

(15)

式中si和σHj為應力的粘性部分。

LéVESQUE等[17]已經證明,建立本構模型時在Schapery模型中引入不同的非線性函數依然滿足熱力學基本定律,且不對Clausius-Duhem不等式產生影響。因此,非線性粘彈性本構模型中的能量耗散采用了和線性模型一致的計算公式。

2 本構模型的二次開發

為模擬聚合物循環過程中的熱力耦合,有限元仿真主要采用了下列兩種方法：

(1)將材料受載后的自熱視為內部熱源,通過有限元軟件子程序的拓展,先進行力學分析,然后將計算而來的內部熱源應用到溫度場的求解中[18-19]。RIAHI等[20]、SONG等[21]和LUO等[22]針對不同聚合物材料進行了相關研究。

(2)建立準確可靠的本構模型,通過熱力學基本定律,可以從本構模型中獲取能量耗散的表達式,從而在有限元分析中同時求解熱學和力學問題[23]。依此方法,針對具體研究對象選取適當的自由能函數形式,引入適當的內變量來描述不可逆變形過程中的材料內部微結構的變化,即可獲得材料的本構關系,然后就可以從能量平衡方程中推導出熱力學變形過程中的溫度控制方程[24]。

為了實現完全耦合形式的熱力分析,本文選擇第二種方法。

2.1 數值算法

應力表達式為σ(t)=s(t)+σH(t)l,其中：

(16)

其中,s∞(t)和σH∞(t)為彈性部分;si(t)和σHj(t)為粘性部分,它們的表達式如下：

(17)

根據gi(σ)的表達式,gi(σ)也是關于t的函數,為了簡化,記gi(t)≡gi(σ(t))。給定時間增量[tn,tn+1],則tn+1時的應力偏量s∞(t)為

(18)

si(tn+1)為

(19)

為了獲得應力更新方程,令

(20)

由于t=tn+1時應力是未知的,因而gi(tn+1)也是未知的。若時間增量步Δt很小,可以忽略非線性函數在這一時間區間內的變化,作出以下假設：g1(tn+1)≈g1(tn)、g2(tn+1)≈g2(tn)。應力偏量部分可簡化為

(21)

其中

(22)

同樣地,對于應力的球量部分,應力更新方程為

(23)

(24)

其中

(25)

綜合可得

(26)

其中

(27)

Jacobian矩陣定義為

(28)

2.2 非線性模型子程序

Abaqus擁有用戶材料子程序,可方便地對材料本構模型進行二次開發,在高聚物力學特性的數值模擬中得到了廣泛的應用。本文選擇UMATHT與UMAT聯合使用來實現完全耦合的熱力分析。在時間增量步中,UMAT通過狀態變量“rpl”(rpl的值即為式(12)中的φmec)存儲積分點處由于機械加載引起的能量耗散。UMATHT提供了熱流矢量,定義了材料的熱本構關系,根據產熱方程求解熱傳遞問題。圖1是執行子程序的流程圖。

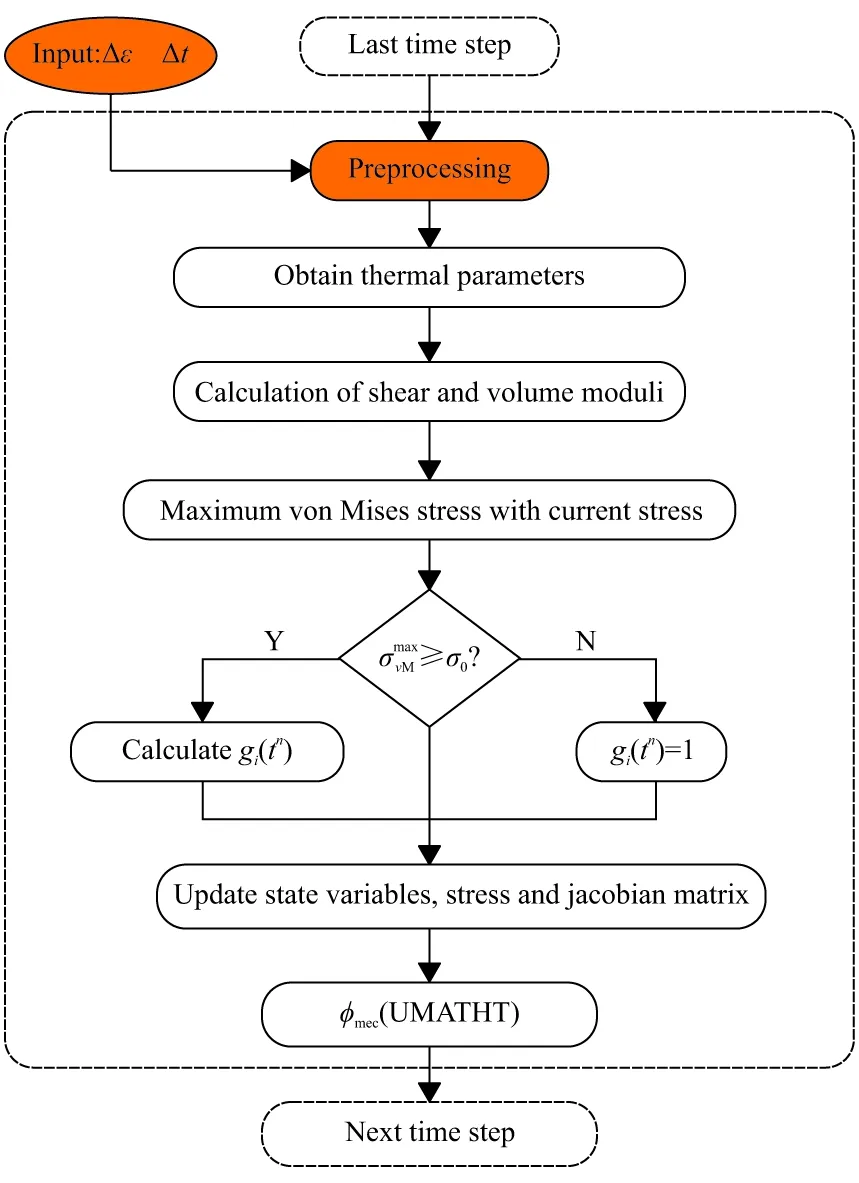
圖1 子程序UMAT和UMATHT流程圖Fig.1 Flowchart of UMAT and UMATHT

由于復合推進劑是對溫度敏感的材料,應力場和溫度場相互影響,因而本文采取了完全耦合的熱力分析方法。在完全的熱力耦合分析中,耦合方程的矩陣表達式為

(29)

式中 Δu和Δθ分別為位移增量和溫度增量;Kij為分矩陣;Ru和Rθ分別為力學和熱學殘余向量。

3 仿真結果與分析

模型參數的獲取方法見文獻[25]。利用HTPB推進劑單軸拉伸實驗和應變控制的單軸循環實驗對本構模型的仿真結果進行驗證,試驗材料、設備和試驗流程的具體說明可參考文獻[26],在此不再贅述。仿真時物理模型的幾何形狀與尺寸與真實啞鈴型試件一致,邊界條件與實驗一致,試件的一端固定,另一端施加位移載荷,見圖2,選擇試件標距段中部作為分析區域。環境溫度根據實驗要求設定。試件與環境之間為自然對流換熱,試件表面的熱邊界條件為

圖2 Abaqus/CAE中試件邊界條件示意圖Fig.2 Schematic diagram of boundary conditions of the specimen in Abaqus/CAE

q=-h(Ts-T∞)n

(30)

式中h為試件與環境之間的對流換熱系數;Ts為試件表面溫度;T∞為環境溫度;n為表面的法線方向。

3.1 單軸加載

聯合使用子程序UMAT和UMATHT,以模擬復合推進劑由于機械載荷引起的自熱效應,探討其對復合推進劑力學響應的影響。在自熱效應的有限元仿真中,UMATHT中的導熱系數和比熱容是常數,不隨溫度變化而變化。HTPB推進劑試件與空氣之間的對流換熱系數h設置為10 W/(m2·K)。

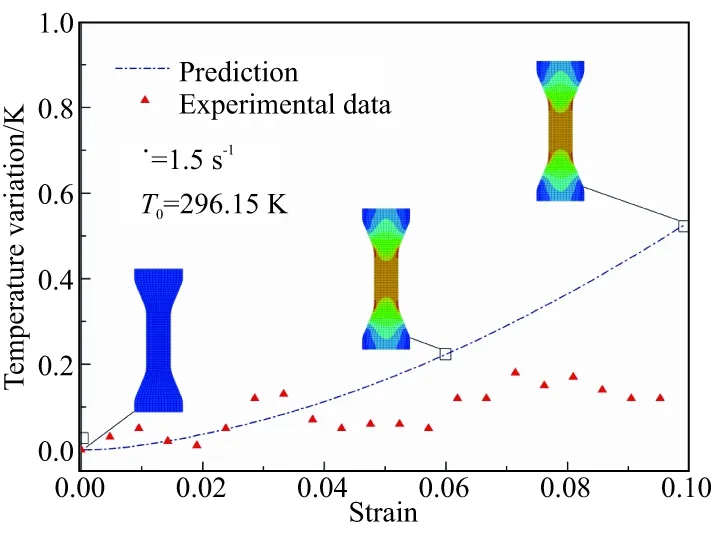
圖3 單軸拉伸實驗中的自熱效應Fig.3 Self-heating effect in uniaxial tensile test

圖4顯示了自熱效應對于單軸應力-應變關系的影響,未考慮自熱效應的預測曲線是在等溫條件下獲取的。由于能量耗散導致了溫升,HTPB推進劑受熱而軟化,因此預測的應力整體偏小。

圖4 自熱效應對單軸應力-應變關系的影響Fig.4 Effect of self-heating on uniaxial tensile stress-strain relations

為反映自熱效應與應變率之間的關系,還進行了常溫下其他應變率下的仿真,見圖5。隨著應變率的提高,外載荷做功越劇烈,能量耗散越來越多,自熱效應也越來越顯著。該發現揭示了高聚物材料變形中自熱效應的應變率相關性,為了更精確地描述材料的力學性能,建立本構模型時需根據變形與加載速率等條件考慮材料自身溫度的改變。對復合推進劑而言,在高應變率加載的大應變情形下,自熱效應較顯著[27]。

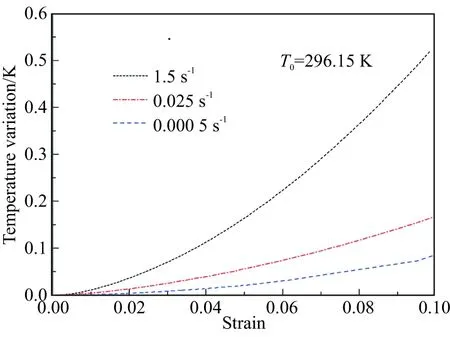
圖5 不同應變率下的自熱效應Fig.5 Self-heating effect under various strain rates

3.2 循環加載

為了明確自熱效應對循環行為的影響,隨后對受循環加載的HTPB推進劑試件進行了完全熱力耦合形式的有限元仿真。圖6是試件加載過程中典型的溫度云圖(加載條件為f=50 Hz,εa=0.03)。可見,試件的標距段的溫度由于材料力學耗散而升高,軸向(與試件加載平行的方向)上存在溫度梯度,這與實驗觀測一致。圖6中還給出了中心區域截面的溫度云圖,截面核心溫度與邊緣溫度相差極小,因而可認為試件內部實現了溫度平衡,各空間點的溫度趨向一致,溫度場在這一截面是均勻分布的,這也進一步證明了此前實驗分析中利用表面溫度表征HTPB推進劑力學性能的合理性。

圖6 循環加載中試件典型的溫度云圖Fig.6 Typical temperature contour of the specimen in cyclic loading

采用對稱建模可以減少工作量,既不影響計算結果又可提升計算效率。由于需要同時使用兩個子程序,考慮試件的對稱性,在后續的仿真中選取試件的一半進行分析。從文獻[28]可知,由于HTPB推進劑力學性質的溫度相關性,自熱效應引起的溫升影響著HTPB推進劑動態應力-應變關系的預測。本文進行了多種加載條件下的自熱效應模擬,得到了試件標距段表面溫度隨時間的變化,結果見圖7。

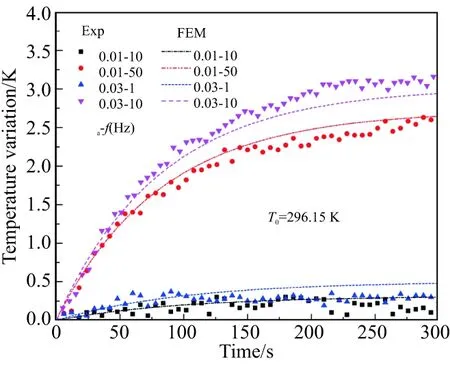
(a)Strain amplitude 0.01～0.03

由圖7可見,由于開始時試件和環境的溫差較小,對流過程中熱量損失也比較少,試件的產熱速率大于試件和環境的熱交換率,因而溫度在一段時間逐漸上升;隨著循環時間的增加,試件表面溫度與環境溫度通過熱對流而達到平衡,表面溫度保持相對穩定的狀態。綜上,仿真預測結果與實驗中測得的溫升較吻合,驗證了本構模型和數值算法的正確性。

圖8給出了不同仿真條件下循環應力-應變關系的對比圖。可以發現,與不考慮自熱效應相比,滯回圈的斜率降低,表明力學性能已受到自身溫度升高的影響。在熱力耦合分析中,考慮自熱效應后,滯回圈的形狀與實驗結果更為吻合,非線性熱粘彈性本構模型的預測精度得到提高,表明計及自熱效應的熱力耦合型本構模型能更準確地描述HTPB推進劑的循環力學行為。

為了定量評估模型的預測效果,計算了滯回圈斜率的誤差,見圖9。由圖9可知,模型的預測與實驗之間的誤差均在10%以內,表明與文獻[28]相比,本構模型的預測能力得到了提高,有力佐證了自熱效應在本構模型應用中的重要性。

(a)f=10 Hz,εa=0.01 (b)f=1 Hz,εa=0.03 (c)f=10 Hz,εa=0.03

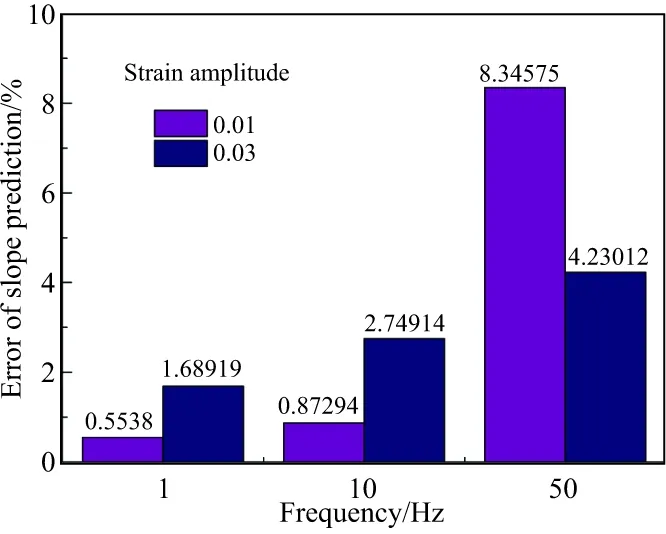
圖9 滯回圈斜率的預測誤差Fig.9 Prediction errors of the slope of the hysteresis loop

4 結論

(1)對于循環加載下的復合推進劑,自熱效應較單軸加載狀態更顯著(最大溫升為15 K),需要在本構模型中加以考慮。

(2)自熱效應對復合推進劑的力學行為有著直接影響,與不考慮自熱效應相比,循環加載下應力-應變滯回圈的斜率降低,其力學性能的劣化受到自熱效應的直接影響。

(3)本構模型成功表征了復合推進劑在不同加載模式下的非線性力學行為和自熱效應,模型預測的滯回圈斜率與實驗之間的誤差均在10%以內。該研究為高能固體聚合物的熱力學表征提供了參考。