一類綜合控制系統的動態輸出反饋H∞控制器設計

孫 鳳 琪

(吉林師范大學 數學與計算機學院,吉林 四平 136000)

控制理論在數學、計算機科學以及工程學等領域應用廣泛[1-3].在控制系統中,輸出測量只能局部反應受控系統信息而不能全局實施系統鎮定,從而影響實際控制效果,利用靜態和動態輸出反饋H∞控制可有效解決該問題,對時滯、奇異攝動和不確定性綜合存在的系統性輸出反饋H∞控制器設計已引起人們廣泛關注[4-5].輸出反饋H∞控制是在H∞空間通過某些性能指標的無窮范數優化而獲得控制器的一種控制方法,廣泛應用于控制工程等領域[6-8].文獻[7-9]設計了帶有記憶的動態輸出反饋H∞控制器以及新的切換規則,為不確定多時滯線性切換系統的理論研究提供了更多可能性,但未考慮奇異攝動性; 文獻[10-11]設計了狀態反饋非脆弱H∞控制器,設計方法復雜,該方法需引入較多的矩陣變量,使計算量較大,推理過程繁瑣,且未引入矩陣工具箱手段,不便于實際應用; 文獻[12-13]研究了廣義系統以及時變時滯狀態下的動態輸出反饋H∞控制器設計問題,但僅針對時滯控制系統,所得的結果受限.

本文在此基礎上,對具有奇異攝動、不確定性和時變時滯的綜合控制系統進行輸出反饋H∞控制器設計,運用Lyapunov穩定性理論和矩陣分析理論,選取適當的交叉項界定法,推出滿足H∞性能指標的動態輸出反饋H∞控制器設計新方法,所得結果具有較低的保守性.最后用數值算例驗證結論的可行性.

1 無記憶動態輸出反饋H∞控制器設計

考慮如下具有控制輸入和干擾輸入的不確定性時變時滯奇異攝動控制系統

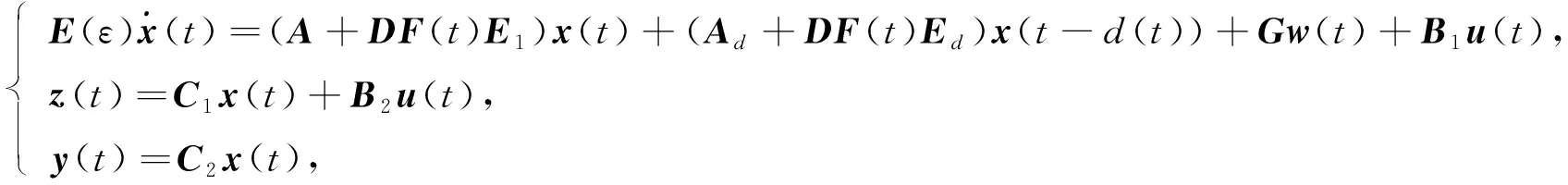
(1)

(2)

τ,μ為已知的實常數,F(t)∈i×j為具有Lebesgue可測元的適當維數的不確定矩陣,其不確定性滿足范數有界條件

FTF≤I.

(3)

設計無記憶動態輸出反饋H∞控制器

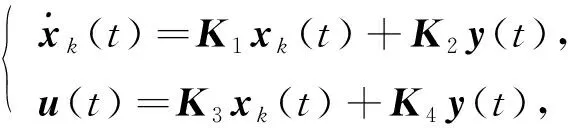
(4)

其中xk∈nk為控制器狀態,nk為控制器階數,r≤nk≤n,K1,K2,K3,K4為待確定控制器的參數矩陣,則閉環系統為

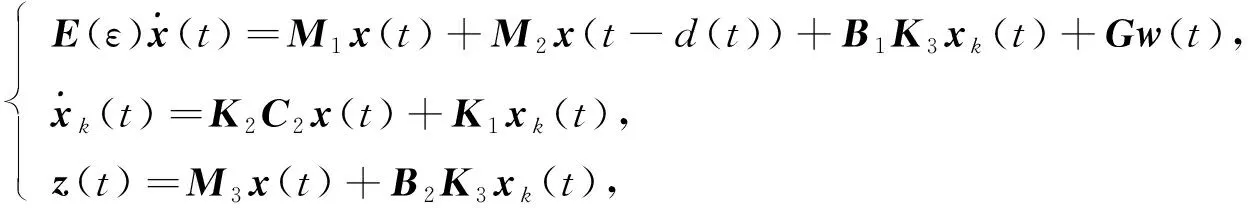
(5)

其中M1=A+DF(t)E1+B1K4C2,M2=Ad+DF(t)Ed,M3=C1+B2K4C2.

下面在時滯依賴情形下,設計無記憶動態輸出反饋H∞控制器(4),即對給定的性能指標γ>0,若閉環系統(5)滿足如下條件:

1) 當w(t)=0時,系統是漸近穩定的;

2) 在零初始條件下,?w(t)∈L2[0,∞)從外部干擾w(t)到被調輸出z(t)傳遞函數的H∞范數滿足Gzw(s)<γ,即‖z(t)‖2<γ‖w(t)‖2,則系統(1)是漸近穩定的,且滿足給定的H∞性能指標.

本文所有定理均在滿足文獻[14]的引理2.1條件下成立.

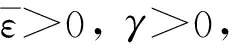
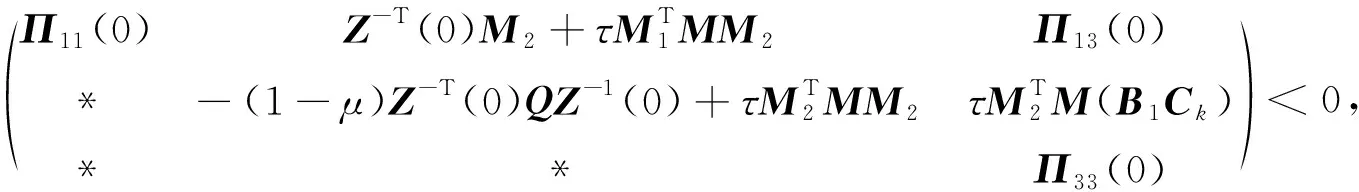
(6)

(7)

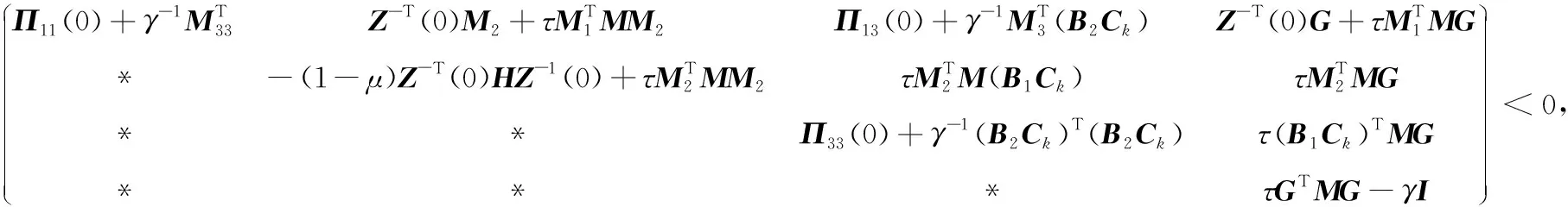
(8)

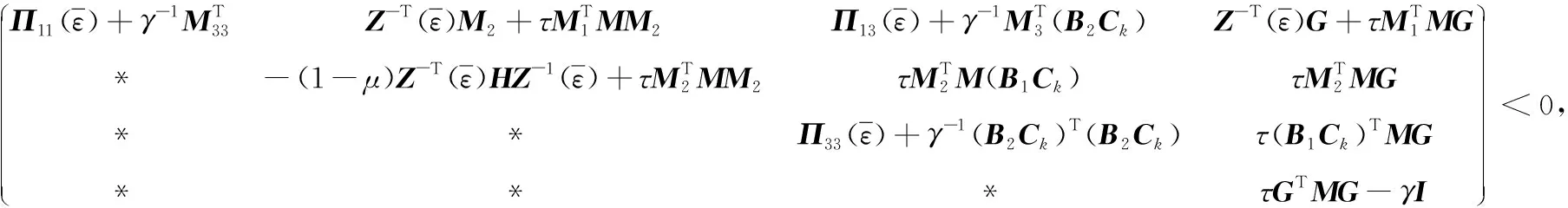
(9)

其中

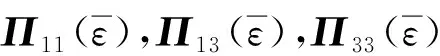
證明: 不妨假設w(t)=0,構造新的依賴控制器狀態的Lyapunov-Krasovskii(L-K)泛函

V(x(t))=V1(x(t))+V2(x(t))+V3(x(t))+V4(x(t)),

其中

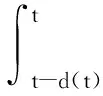
Q,M,H為待定適當維數的正定對稱矩陣,則V(x(t))>0.

將V(x(t))沿系統(1)的任意軌跡進行微分,由文獻[14]引理2.5可知,存在適當維數的矩陣P,對稱陣N和R,使得

由于

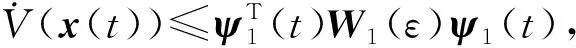
其中

當w(t)≠0時,同理可證

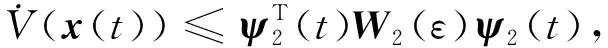
其中

其中

故

其中

(10)

矩陣不等式(10)<0關于未知變量γ,Ak,Bk,Ck,Dk,H,Q,M,N,P,R和Z(ε)是非線性的,進行線性化處理后,可得如下線性化定理.

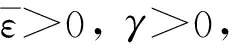
其中

Ω11(0)=ZT(0)AT+(B1K4)T+AZ(0)+B1K4+Q-N+ηDDT,

Ω15(0)=ZT(0)AT+(B1K4)T+ηDDT,

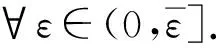
注1定理2是在構造新的Lyapunov泛函基礎上進行研究的,考慮的系統是綜合控制系統,可采用不同的交叉項界定,進而推出更優越的穩定性判據.

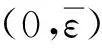
2 記憶動態輸出反饋H∞控制器設計

對系統(1),設計記憶動態輸出反饋H∞控制器為

其中xk∈nk為控制器狀態,nk為控制器階數,r≤nk≤n,Ak,Bk,Ck1,Ck2,Dk1,Dk2為待確定控制器的參數矩陣,則閉環系統變為

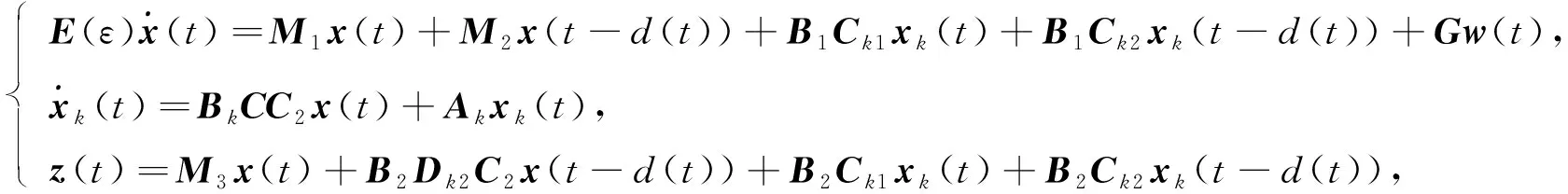
(11)

其中M1=A+DF(t)E1+B1Dk1C2,M2=Ad+DF(t)Ed+B1Dk2C2,M3=C1+B2Dk1C2.

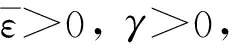
其中

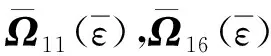
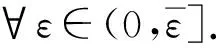
類似于定理2的證明過程,故略.

3 算 例

考慮文獻[15]中的數值算例

其中

取H∞性能指標γ=1.1,小于文獻[15]中的H∞性能指標γ=1.561 7.為與文獻進行對比,考慮系統不含輸出的情形.在奇異攝動系統(1)中,令

對于時滯,假設其滿足

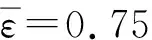
Z1=0.326 9,Z2=0.223 7,Z3=0.014 7,Z4=0.005 9,Z5=-0.038 8,η=0.172 4,

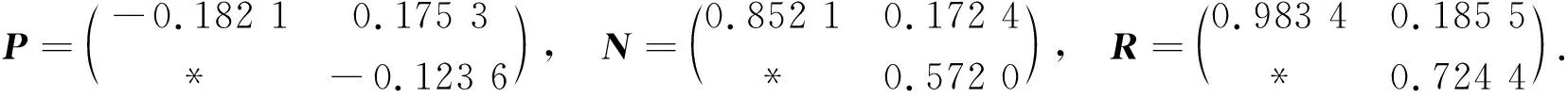
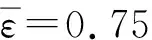
綜上,本文對具有時變時滯、魯棒性和奇異攝動的綜合控制系統進行輸出反饋H∞控制器設計,在構造含有攝動相關的L-K泛函基礎上,設計了新的無記憶和記憶動態輸出反饋H∞控制器.通過對比現有文獻,所得的結果具有較低的保守性[15-17],適用于標準和非標準情形,可為H2/H∞控制、H∞濾波以及電力系統等領域的控制問題提供理論參考[18-20].