小學數學運算一致性的教學理解

【摘 要】《義務教育數學課程標準（2022年版）》將數的認識與數的運算進行了整合，對數與運算的教學提出了新的要求。加深對數概念的一致性、運算意義的關聯性、數與運算的整體性、算理和算法的一致性、運算規律的共通性的教學理解，將有助于教師把握新課標精神，引導學生探索運算一致性，促進學生加強知識間的相互聯系，從而使學生形成更為整體而結構化的數學知識。

【關鍵詞】小學數學；運算教學；數的運算；運算一致性

【中圖分類號】G623.5? 【文獻標志碼】A? 【文章編號】1005-6009（2023）14-0024-04

【作者簡介】劉久成，揚州大學（江蘇揚州，225002）教育科學學院教授，博士生導師，主要研究方向：數學課程與教學論研究。

培養小學生的運算能力是歷次課程改革不容回避的問題，重視發展學生的運算能力，是我國數學教學的特色所在。然而，從教材和教學的實際來看，認數始終作為運算的前提條件，不同數的認識有不同的背景和獨特的方法。比如，整數（指自然數）強調計數，小數注重聯系現實生活，分數強調等分事物。數的運算也有各自的算理，對整數、小數、分數的算法也進行了不同的歸納。總之，算理未能凸顯數的意義和本質，算法之間也缺乏聯系。

《義務教育數學課程標準（2022年版）》提出課程內容要進行結構化整合，把“數的認識”與“數的運算”整合為“數與運算”這一個主題，包括整數、小數、分數的認識及其四則運算。如此，溝通了數的概念與數的運算之間的關聯，有助于學生從整體上理解數與運算的知識和方法，感悟數與運算之間的密切聯系，體會數的運算本質上的一致性，也將促進學生數感、符號意識、運算能力、推理意識等核心素養的提升。如何理解落實這一新的要求，引導學生對運算一致性進行探索，促進學生加強知識間的相互聯系和對數學本質的認識，從而使其形成更為整體而結構化的數學知識呢？筆者認為，可以從以下幾個方面著手展開探索。

一、數概念的一致性

數量來自對事物（事件、物體）量的表達，而數正是對數量抽象化的結果。小學生所認識的數主要是整數、分數和小數，這些都是對現實世界事物數量的抽象，對它們的認識是學習數學最重要的基礎。

數的形成經歷了一個漫長的過程，從實物符號記數到象形符號記數，再到數字符號記數。記數方法也多種多樣，如采用加減法原則的羅馬數字記數制、采用位值原則的阿拉伯數字記數制等。采用位值原則的十進制計數法由于只要1、2……9、0十個數字以及計數單位就能表示任意大小的數而被普遍采用。可以說，十進制計數法是數學史上無與倫比的光輝成就。從數的構造來看，計數單位是構造數的基礎，也是認數的關鍵，有了計數單位，同一個數字出現在不同的數位上就表示不同大小的數。

認識整數時，1～9的認識比較容易，10的認識就相對比較困難。9加1是十個1，十個1是1個“十”，1個“十”如何表示呢？用1來表示就會與1個“一”相混淆，如果用太多符號表示也不方便，這時人們想到用“10”來表示。十位上的“1”表示1個“十”，個位上的“0”表示沒有，是用來占位的。這樣，學生能感受到十進制計數法的特點，認識到位置值的重要性以及“0”占位的必要性。隨著認數的擴大，由一個一個地數到十個十個地數、百個百個地數……學生感受到記數的過程就是計數單位的創造過程，計數單位的重要性也就凸顯出來了。

分數的產生來源于多方面的需要，分數不僅可以比較大小，而且具有運算功能。認識分數時，分數的計數單位（也就是分數單位）同樣是表示分數的關鍵。任何一個分數都是若干個分數單位的累加。分數單位雖有大小之分，但不是十進制，也沒有明確的倍數關系，教材和教學對此都強調不夠，以至于學生認識不到分數也有計數單位。

小數是基于十進分數定義的，具有十進位制的特點，可以與整數一起構成一個完整的位值制系統。每一個整數或小數的大小，不僅取決于表示它的數字符號，還取決于這些數字符號所在的位置值，即它的計數單位。

因此，計數單位是構造數的共同基礎，整數、小數、分數都可以看作計數單位的“組裝”，認識數的核心在于認識計數單位，計數單位的統領作用是數概念的一致性所在。

二、運算意義的關聯性

數概念是運算的基礎，通過運算不僅能反映引進數的價值，而且可以加深對數概念的理解。集合論是現代數學的基礎，自然數的四則運算都可以基于集合的基數理論和序數理論進行定義。

在基數理論中，自然數的加法的和是指兩個不相交的有限集合A、B的并集C的基數；自然數的減法的差是指一個有限集合A與其子集B的差集C的基數；自然數的加法與減法的結果都可以通過數數獲得，既可以數并集與差集中元素的個數，也可以在集合A的基數上繼續數出b個1來，或者在集合A的基數上往回數出b個1來。“一”是最基本的計數單位，這一點小學生容易理解，小學數學教材中通常也是這樣幫助學生理解加減法意義的。

自然數的乘法同樣可以用集合的基數來定義。兩個有限集合A、B的基數分別是a、b，由A中取一個元素u，B中取一個元素v，組成一個有序數對（u、v），所有這樣的有序數對構成的集合稱為A和B的笛卡爾乘積集合A×B（也叫直積集合A×B），其基數就是a與b的積。在小學數學教材里，乘法是用“同數連加”的方法來定義的，其實兩者可以統一起來。比如，3+3+3+3按同數連加表示成3×4或4×3，也可以表示成每排有3個○，共4排，形象地表示成一個方陣，這就形成了笛卡爾乘積集合。

自然數的除法是指把有限集合C（基數c）恰好分成a個有相同基數b的子集B，記作c÷b=a。分成a個有相同基數b的子集，表明從c中連續減去a個b，所以除法又可以看作“同數連減”。小學數學教材中除法的引入通常結合分東西，“每份分得同樣多，可以分成幾份？”就運用了除法的集合意義。這樣理解除法比較直觀，具有可操作性，也利于學生感受除法的實際價值。

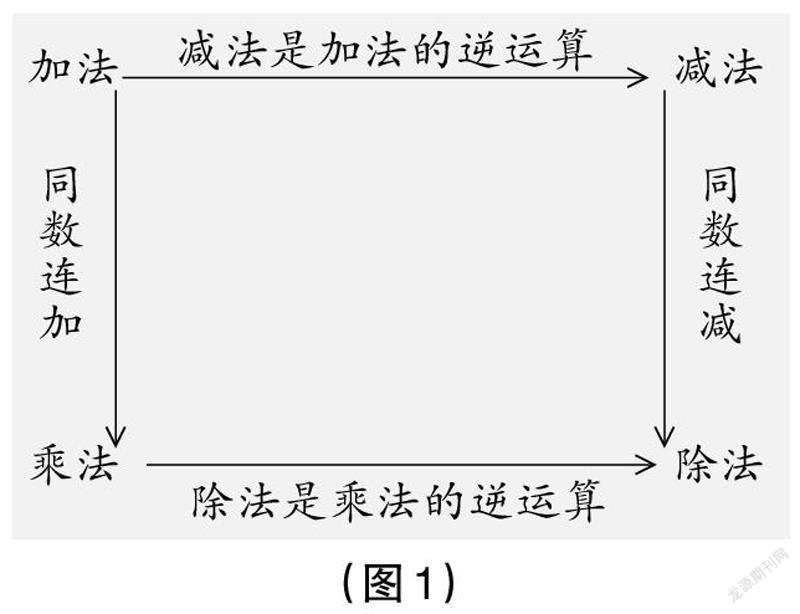
數的運算從更抽象的層面都可以看作集合A×A到A的對應，也就是對于集合A×A中的序偶（a₁，a₂），集合A中都有唯一確定的元素a與之對應，我們就說集合A上定義了一種運算。這也反映了數的運算在高階抽象層面上的一致性。小學數學中所說的運算，是指定義在整數、小數、分數集合上的運算，包括加法、減法、乘法和除法四則運算，也稱算術運算。它們之間的關系可以通過下圖1簡單加以表明。可見，減法和乘法是在加法的基礎上衍生出來的，除法既可以看作同數連減的簡便運算，也可以看作乘法的逆運算，所以，加法是其他三種運算的基礎。

從集合的序數意義出發，也可以給出自然數四則運算的定義。由于基數意義下的四則運算相對直觀，易于理解，通常為小學數學教材所采用。

三、數與運算的整體性

首先，我們必須看到數與運算密切相關，數失去運算也就沒有意義了。數的認識包括數的表達與數的大小，整數、小數的表達有賴于記數符號和位值概念，任何一個整數或小數都是不同計數單位的數相加的結果，而每一個位置上的數又都是該數字值與其位置值的積，如個位上的3是3×1的積，十位上的3是3×10的積，百位上的3是3×100的積。因此，整數或小數的認識離不開運算。同樣，任何一個分數也都可以看作由幾個分數單位相加得到的，如3/5是3個1/5相加的結果，這可以通過圖形直觀來說明。數的大小也與運算有關，如在自然數的認識中，通過自然數的“直接后繼”（+1）得到后續自然數，這便在定義自然數時給出了自然數的加法。隨著認數增大，出現更大的計數單位“十”“百”“千”“萬”等。不難看出，整數、小數的加減法本質上是相同計數單位的數的累加與遞減；分數相加減時，從分數的意義出發，需要統一分數單位。因此，無論是整數、小數還是分數的認識，都與運算密不可分。

其次，數的認識與運算分別是陳述性知識與程序性知識。教育心理學研究表明，陳述性知識是學習程序性知識的前提條件，程序性知識的形成會促進新的陳述性知識的掌握。因此，單純教學數的概念意義不大。有學者指出，只向學生傳授陳述性知識是遠遠不夠的，必須把陳述性知識的教學與程序性知識的訓練有機結合起來。［1］學習四則運算必須通過理解算理達到掌握算法，而對算理的理解必須依據對數的意義和運算意義的理解，就像整數、小數和分數相加減，都要歸結為相同計數單位（分數單位）上的數相加減。讓學生從數的意義和計數單位的視角理解算理，建立起概念性知識和程序性知識的聯系，有助于他們形成整體性的知識結構。

四、算理和算法的一致性

審視歷次教學大綱或課程標準，都強調算理、算法的重要性。算法是指在解相同類型的計算或問題的時候，按照一定的計算方法和步驟總能得到結果的程序。［2］算理則是指說明這種程序的合理性或理論依據。

在小學數學四則運算中，整數加減法強調相同數位對齊，小數加減法強調小數點對齊，分數加減法則強調分母相同才能直接相加減。其中，算法的一致性是明顯的，也就是要求相同計數單位的數才能直接相加減。其算理在于，整數、小數、分數的四則運算本質上都是對計數單位進行運算，加減法表現為對計數單位的累加或遞減，由于乘法是“同數連加”，除法是“同數連減”，作為加減法的高級運算，乘除法仍然可以看作對計數單位的累加或遞減，在算理上是一致的。從另一個角度來看，比如，整數乘法也可以通過將乘數拆分成不同計數單位的數的和，再依據運算律進行運算，如24×3=（2×10+4×1）×（3×1）=（2×3）×（10×1）+（4×3）×（1×1）。也就是計數單位上的數與計數單位上的數相乘，計數單位與計數單位相乘，再把相同計數單位上的數合起來。這樣的橫式展示了整數乘法的算理，小數乘法、分數乘法以及除法運算的算理也可以類似說明。不過，如此說明需要以運算律和有關運算性質為基礎，適合在中高年級的適當階段或單元復習整理時進行概括，這也是新課標在第二、三學段的“教學提示”中提出要求的原因所在。

五、運算規律的共通性

規律是指事物之間內在的必然聯系。整數、小數和分數的四則運算有許多規律性知識，比如，加法交換律、結合律，乘法交換律、結合律、分配律，乘法運算中積的變化規律，除法運算的商不變性質等，將它們加以聯系和貫通，有助于學生加深對運算意義及運算規律的本質認識，并進行有效遷移。

比如，在整數運算中總結出來的加法交換律、加法結合律、乘法交換律等，隨著數域的擴大，常常直接拿來使用，一般不進行說理或證明。其實這正是讓學生感受和理解算法一致性的素材。比如，整數乘法交換律對于分數乘法而言同樣適用，我們可以結合圖形直觀稍作說明：1/3×1/4，可以表示先分一個矩形的1/3，再分其中的1/4；也可以表示先分這個矩形的1/4，再分其中的1/3。由此可見，1/3×1/4=1/4×1/3是相等的。對此，學生是不難理解的。

再如，商不變的性質是在整數除法中總結出來的重要規律，不僅可以用于整數除法運算的簡化，也適用于小數除法和分數除法運算，在整數、小數和分數除法中具有共通性，這一點不難理解。此外，商不變的性質在除法、分數、比中也具有共通性。我們知道，除法、分數、比這三個概念的來源不同，除法是作為乘法的逆運算引進的，在已知積和一個因數時求另一個因數；分數通常為了表示平均分時部分與整體的關系，或者說表示除法運算的結果；比實際上是把兩個量進行比較，以一個量去衡量另一個量，當兩個量的順序調換時，就會得到另一個比。三者的概念有一定區別，但它們又聯系密切，可以從“測量”的角度加以統一。當用一條較短的線段a去測量另一條較長的線段b時，如果測量三次剛好量盡，我們可以說：線段b的長與線段a的長的比是3∶1；用除法運算來說就是線段b中包含有3個線段a；用分數來說就是線段b的長是3份而線段a的長只占1份，線段a的長是線段b的長的1/3，或者說，線段b的長是線段a的長的3/1。由于這三個概念可以表達同一件事，具有共通性，相應地，除法的商不變性質、分數的基本性質、比的基本性質也就可以統一起來。如果把分數線和比號看作除號，那么分數的基本性質、比的基本性質和除法的商不變性質就是一致的。即除法中的被除數和除數，分數中的分子和分母，比的前項和后項，都同時乘或除以一個相同的數（0除外），其結果不變。這種一致性還體現了數學中“變中不變”的思想，從運動和變化中發現不變的因素，從看似不同的事物中尋找共同的特征，是數學學習的重要方法。

【參考文獻】

［1］張大均.教育心理學［M］.北京：人民教育出版社，2004：148.

［2］張奠宙，孔凡哲，黃建弘，等.小學數學研究［M］.北京：高等教育出版社，2009：292.