艦載機通用質量特性指標論證

祝華遠，李軍亮，張陜輝，郭 森

(1. 海軍航空大學青島校區，山東 青島 266041；2. 北京質遠恒峰科技有限公司，北京 100010)

0 引 言

通用質量特性指標是裝備壽命周期管理的重要對象，貫穿于裝備論證、設計、生產、使用和退役報廢的各個階段。通用質量特性指標研究包括指標論證、分配、驗證與評估等多項內容，其管理水平直接影響武器裝備的作戰效能發揮[1–3]。在裝備綜合保障的體系中，作戰需求牽引著裝備的發展和運用、保障系統的設計與運行，而保障系統則會影響裝備系統的作戰效能發揮。從本質上講，通用質量特性指標論證與優化，是在把握裝備作戰任務要求的基礎上，對裝備各項性能和保障系統設計的論證與優化，通用質量特性指標評估是對保障對象和保障系統及其適用性的度量，是指標論證與優化的重要手段。因此，通用質量特性指標論證的科學性與評估的準確性對于裝備發展論證、迭代設計、作戰使用等有著重要作用。

艦載機作為航母編隊的主要戰斗單元，其作戰效能的發揮對航母體系的影響至關重要。但影響艦載機作戰適用性的因素較多，艦載機在使用過程中受到惡劣的自然環境和苛刻的平臺環境影響，存在2 項主要矛盾：一是高可靠要求與高故障率之間的矛盾[4–8]，二是快速出動能力與強艦基約束之間的矛盾。前者主要指高溫、高鹽、高濕的海洋環境易導致艦載機機體和機載產品發生故障與艦載機高可靠要求之間的矛盾；后者主要體現在艦面有限空間約束、母艦多自由度運動與艦載機保障作業流程復雜、保障強度高之間的矛盾。為了解決這兩項矛盾，就需要在裝備設計之初對裝備的各項通用質量特性指標進行科學論證，從而以各項指標為依據規劃裝備全系統全壽命周期的管理工作。

目前通用質量特性指標論證與優化方法主要有解析和建模仿真兩類。解析方法主要有經典的概率統計模型、模糊評判、貝葉斯分析等[7]；建模仿真方法主要有系統動力學、離散事件、智能體仿真等[8–11]。解析方法主要針對單一指標的設計與分析，如在可靠性指標設計過程中如何將整機級可靠性指標向系統級、分系統級或者關鍵部件分配等。仿真方法可以實現多指標一體化論證，基于裝備的總體效能要求對可靠性、維修性、保障性指標與作戰性能等的統一論證，可根據仿真結果進行單項、多項指標的靈敏度分析，從而對指標在閾值范圍內進行調整優化，這是以后指標論證與優化的主要趨勢。但是目前在工程實踐中，指標論證的頂層輸入不夠明確，即型號作戰任務要求向裝備作戰性能與通用質量特性指標轉化的定量分析方法不夠完善。雖然近些年來，越來越重視裝備的體系貢獻率，但還不能將裝備體系貢獻率與裝備通用質量特性論證的映射關系清晰表述[12]。體系貢獻率涉及諸多不確定性因素，因為構成裝備體系的各系統之間存在涌現性、非線性、隨機性等特點，制約到裝備體系貢獻的度量與評估。

針對上述問題，設計面向作戰任務的艦載機通用質量特性指標論證流程，構建論證模型和優化模型，并結合算例，說明設計方法的可行性，從而提高論證科學性與精確性。

1 面向作戰任務的艦載機通用質量特性指標論證

隨著新型艦載機結構一體化、輕質化和隱身化等要求的提升，機載產品集成化、模塊化、可測化的水平增強，要求新型艦載機具備可靠性高、故障自診斷能力強、環境適應性好、易于維護保障的特性，保證較高的作戰適用性和艦機適配性。但艦載機在使用過程中受到自然環境、平臺環境、保障系統等諸多因素的影響，保障作業過程中充斥著不確定性和隨機性。為了提高艦載保障作業效率，提高艦載機的出動能力、任務可靠性和任務持續性，必須基于系統工程思想開展艦載機通用質量特性指標論證。

以航母編隊和多機種艦載機的作戰任務要求為頂層輸入，以先進保障理論和技術體系為驅動，深入分析艦基保障平臺和艦載機自身的結構與性能特征，明確艦載機的保障需求，論證艦機一體化的保障性指標體系。包括體系級、系統級和資源級指標（如使用可用度、任務成功率、出動架次率、平均延誤時間、資源利用率等）以及各指標的性能閾值，根據指標要求進一步明確保障系統各要素的設計要求，如保障設備、信息系統、艦面接口數量、布局等的設計，從而做到艦機保障力量運用一體化、保障資源配置優化、信息資源共享化[1,8]。艦載機保障性指標論證總體流程如圖1 所示。

圖 1 艦載機保障指標論證流程Fig. 1 Demonstration process of carrier-based aircraft support indicators

2 基于離散事件的艦載機保障過程建模

對艦基環境下艦載機使用與維修保障過程進行抽象描述，客觀真實地構建由飛行任務和隨機故障驅動的保障活動流程以及保障作業模型。艦載機的綜合保障工作主要涉及了2 類作業[1,8]：1）使用保障作業，如起降、調運、電氣液保障、彈藥保障等專項作業；2）維修保障作業：包括預防性維修與修復性維修作業。完成以上內容需構建出下列基本模型：不同機型艦載機（艦載戰斗機、直升機、固定翼預警機等）的任務模型、飛機平臺模型（艦載機的基本構型、RMS 要求等）、活動網絡圖模型、保障資源模型和輔助優化模型等，其概念模型如圖2 所示。

圖 2 艦載機保障流程建模的基本內容Fig. 2 The basic content of carrier-based aircraft support process modeling

在此基礎上，基于離散事件建模的原理，采用ILSBox-Designer 軟件構建各類子模型。

2.1 任務模型

任務模型用于對作戰單元中裝備所需執行的任務進行建模，其以作戰與訓練想定、裝備使用方案為建模對象，以適當的形式表現任務發生、任務時序、任務之間邏輯關系、任務結構等內容，模型中包括裝備數量、任務時間、任務強度等。

2.2 裝備模型

裝備模型用于對裝備種類、數量、構型以及各功能單元的通用質量特性數據進行建模，是描述裝備及其組成單元特性的模型。

2.3 保障資源模型

保障資源模型以表單方式對人員、備件、設備等保障資源進行建模，描述保障資源的種類、數量、庫存、供應及使用機制等。

2.4 保障組織模型

保障組織包括了基層級，中繼級和庫房等站點和相互間的保障關系。

2.5 保障活動模型

保障過程模型使用活動網絡圖技術，將裝備使用維護過程中的各類工作進行建模，支持裝備的使用保障、修復性維修保障、預防性維修保障等保障活動的構建。

3 面向保障效能的保障指標優化

在艦面作業空間、保障資源等各類約束下，需要對艦載機進行專項使用保障或維修保障，從而為執行作戰任務做好準備。艦載機保障過程是一個確定性與隨機性相結合的動態過程，具有動態與不平衡的特征，保障過程中涉及到多架艦載機、多種保障資源在多個作業階段、多個保障站點之間的有效協調[8,10]。針對保障指標的確定性和保障過程與保障環境的隨機性與不確定性，綜合運用解析與離散事件仿真方法構建艦載機保障指標論證的技術框架，根據仿真結果對保障要素的靈敏度進行分析，并適當調整保障系統的配置，實現保障資源的精確化與保障作業活動的快速化。

圖3 給出了通用的優化仿真基本框架，在具體建模過程中，需要根據描述的方法構建出具體的裝備模型、保障資源模型、保障活動網絡模型等，然后根據具體的任務要求建立相應的優化模型，并結合仿真結果對影響保障效能的因子進行靈敏度分析，進一步合理確定保障指標閾值范圍，也就是優化指標的解空間，不同優化模型可以采取不同的優化算法。

圖 3 基于離散事件艦載機保障指標優化Fig. 3 Optimization of carrier-based aircraft support indicators based on discrete events

4 算例分析

4.1 考慮隨機故障的某型艦載機保障指標評估與優化

在作戰任務明確的情況下，故障是驅動艦載機維修保障的主要事件。為了充分滿足艦載機在惡劣服役環境下的可靠性要求，算例1 主要研究任務周期內可靠性指標對機群保障效能的影響，從而給出基于保障效能約束的可靠性指標優化方法。假設某機群有16 架艦載機，任務周期持續時間60 d，每架飛機的出動準備時間為60 min，任務取消時間為30 min，每次任務須出動2 架飛機，每飛行日固定任務時間為7:00～17:00，間隔2 h 出動一次。分析機群在任務周期內的使用可用度、任務成功率等指標，判斷是否達到規定要求，若不滿足規定要求則進行調整優化。

根據給定的建模方法，基于ILSBox-Designer軟件進行仿真，首先構建型號艦載機模型、構型模型以及任務模型。

構建各種基本模型后，設定仿真參數：仿真次數1000 次，仿真總時間60 d，置信度水平0.95，裝備調度方式為壽命梯次優先。

仿真結束后，相關保障指標的仿真結果如表1所示。

表 1 仿真結果展示Tab. 1 the simulation result

根據仿真結果可知，2 項機群保障效能指標均不滿足規定要求。在裝備保障系統能力滿足保障要求的情況下，裝備故障是影響使用可用度和任務成功率的主要因素。追溯仿真過程的故障信息，各系統在任務期內的故障次數和占比分別如圖4 所示。

圖 4 某型艦載機各系統的故障占比分布Fig. 4 The distribution of fault proportion of each system of a certain type of carrier-based aircraft

可知，氧氣系統的故障占比最高，為28.89%，總共發生了11 次。統計出機群的任務時間，將各項數據代入式（1）可得該系統的平均故障間隔時間為97 h。

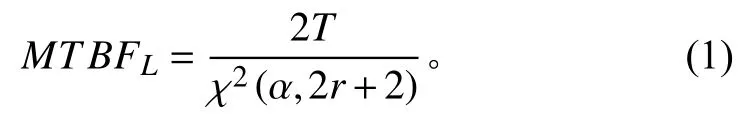
式中：MT BFL為平均故障間隔時間MTBF 單側置信下限，h；T為累積工作時間，h；r為累積責任故障數；α為選定的顯著性水平，α =0.2。

針對國軍標中定義的使用可用度和任務成功率的有限適用性問題，丁定浩[2]在時域維重新推導了戰備完好性參數及其定義，其中使用可用度的定義如下式：

式中：ta=tm+tr；tm為 無故障工作時間；tr為維修時間；γFD為故障檢測率。

任務成功率模型如下式：

式 中，λ ≈1/MT BF。

分析可知，可以根據平均故障間隔時間來調整系統的可靠性設計參數，前提是可靠性參數能夠滿足式（3）和式（2），即滿足以下優化模型：

在滿足式（5）約束條件的前提下，可得系統的MTBF為124 h 時，滿足上述要求，因此可按照該要求對系統進行設計和改型。

4.2 考慮故障預測率的某型機通用質量特性指標評估優化

隨著先進傳感器技術、網絡技術和智能算法的不斷進步，先進艦載機主要采取自主保障模式，故障診斷與預測能力是其中的一項核心能力[13]。因此，在該算例中重點考慮故障預測率對艦載機保障效能指標的影響。假設任務持續時間60 d，每架飛機的出動準備時60 min，取消時間為30 min，每次出動2 架飛機。裝備具備故障預測功能，故障預測率指標分別設置為（0, 0.2, 0.4, 0.6. 0.8, 1.0）。試判斷任務周期內該產品的使用可用度是否大于0.9，任務成功率是否大于0.8。

仿真次數1000 次，仿真總時間60 d，置信度水平0.95，裝備調度方式為壽命梯次優先。

在不同的故障預測率下，任務周期內的保障效能指標見表1，2 項指標基本滿足要求，只有在故障預測率為0 時，單機的任務成功率達不到指標要求。根據分析結果可知，當預測率為（0.2,0.4,0.6.0.8,1.0）時，均滿足任務成功率要求。

仿真模型仿真過程比較復雜，可以較好的刻畫保障過程的不缺性與隨機性，但是很難獲得系統解析模型，只能得到一些離散點的仿真結果，如圖5 和圖6所示。如果將故障預測率設置為連續變量時，仿真時間將會大幅度增加。在獲得復雜系統仿真結果的基礎上，使用代理模型是工程中比較常見的技術手段，其可以根據仿真結果得到簡單的解析模型進行定量分析和迭代。代理模型有多項式擬合、擬合響應面法、支持向量機、神經網絡法等，崔利杰證明了多項式擬合算法在基于離散事件的保障流程仿真中有較好的適用性[11]。在此，設置擬合度大于95%的要求，可得單機在不同故障預測率下的代理模型。

圖 5 故障預測率對使用可用度的靈敏度仿真Fig. 5 Sensitivity simulation of failure prediction rate to operation availability

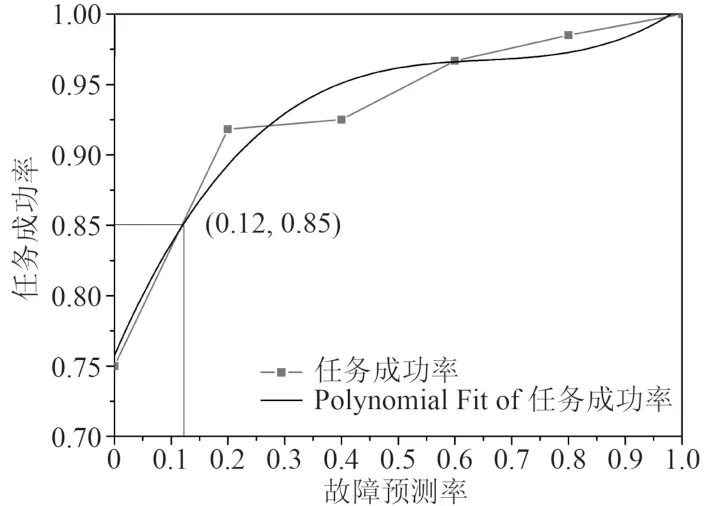
圖 6 故障預測率對任務成功率的靈敏度仿真Fig. 6 Sensitivity simulation of failure prediction rate to mission success rate

使用基于多項式擬合的代理模型，擬合精度約束為0.95，擬合度為0.97，多項式參數分別為：a0=0.975,a=0.0325,b=?0.0582,c=0.052。

使用基于多項式擬合的代理模型，擬合精度約束為0.95，擬合度為0.9，多項式參數分別為：a0=0.75，a=0.92545,b=?1.39，c=0.71。

分析可知，當預測率達到0.12 時可以滿足使用可用度和任務成功率要求，比設定的0.2 的預測率要求要低。在工程中受到產品設計、制造成本等的影響，不同指標精度對應的經濟性必然不同，因此在仿真模型的基礎上使用代理模型可以得到更為精確的數值解，進一步優化通用質量特性指標。

5 結 語

結合艦載機的使用特性，提出艦載通用質量特性指標論證的一般流程，綜合運用解析和離散事件仿真的方法構建了指標論證的基本模型，并基于ILSBox-Designer 軟件進行了仿真。2 個算例分別對故障率和故障預測率的靈敏度進行了評估與優化，結果表明設計方法科學可行，有較好的工程應用性。

雖然研究過程中算例設置比較簡單，但可為復雜工程系統的指標論證與評估提供一種思路。對大型復雜系統，則需要嵌入優化算法，提高仿真效率，如強化學習算法等。

在研究過程中對于裝備經濟性影響沒有解析，后續可以考慮引入裝備的各種成本模型，更為系統地論證裝備的保障指標。