監測信號遲滯對燃氣輪機轉速控制的影響

趙智斌，蔣金生，羅易洲，王 輝，王子楠，劉培軍

(1. 江蘇大學 能源與動力工程學院，江蘇 鎮江 121013；2. 國家管網集團聯合管道有限責任公司西部分公司，新疆 烏魯木齊 830000；3. 中國科學院 工程熱物理研究所，北京 100190)

0 引 言

隨著我國碳達峰碳中和戰略的實施，燃氣輪機將在我國工業系統中發揮重要的作用[1]。由于燃氣輪機監測設備長期需要在高溫、高壓的惡劣環境下工作，監測信號的失真不可避免[2]，進而會造成燃氣輪機控制偏離預期，從而對燃氣輪機整體運行穩定性和安全性造成嚴重的影響[3]。

燃氣輪機監測設備常見問題主要包括監測信號丟失、測量值超限、信號干擾波動，以及監測信號遲滯等。其中，監測信號丟失及測量值超限主要由傳感器內部元器件或接線電纜故障造成[4–6]，盡管這類信號問題會導致燃氣輪機機組跳閘停機等事故[7–9]，但在燃氣輪機控制系統中這類監測故障易于辨識并可實現精確定位和保護。監測設備信號干擾主要由運行環境電磁干擾引發，會造成監測數據的非正常尖峰、脈動[10]，從而造成燃氣輪機工作不穩定，可以通過加強線纜屏蔽及濾波等方法來抑制這一問題。監測信號遲滯問題可能由傳感器測量元器件感應速率慢、監測信號傳輸速率、傳感器精度誤差等多方面因素引發，在所有監測設備問題中最不易快速辨識和調控。存在監測信號遲滯時，對于基于多監測信號進行綜合判斷的燃氣輪機燃料量及轉速目標量，往往與燃氣輪機實際控制需求產生偏差，造成燃氣輪機性能達不到預期甚至會在起動過程中造成冷熱懸掛問題。

本文通過Matlab/Simulink 仿真平臺搭建工業燃氣輪機仿真模型、監測信號遲滯模型和燃料量控制算法，主要研究監測信號遲滯對燃氣輪機轉速控制的影響規律及監測信號在不同遲滯程度時PID 控制參數對燃氣輪機轉速控制性能的影響規律。

1 仿真模型的構建

為復現燃氣輪機監測信號遲滯現象，基于Matlab/Simulink 建立監測信號遲滯模型、燃氣輪機模型和轉速控制邏輯，并將三者進行了耦合，構成具有監測信號遲滯功能的數字仿真系統[11]。建立的具有監測信號遲滯功能的數字仿真系統基本結構如圖1 所示。

圖 1 具有監測信號遲滯功能的數字仿真系統Fig. 1 Digital simulation system with monitoring signal hysteresis function

1.1 燃氣輪機模型

燃氣輪機模型采用機理建模法[11–13]進行建模，包含壓氣機、燃燒室、動力透平等部件，主要用于模擬提供燃氣輪機在控制系統控制下的監測反饋信號。

1.2 轉速控制邏輯

燃料量是改變燃氣輪機運行狀態的最主要控制變量，通過改變燃料量可以控制燃氣輪機完成加速或減速動作。

控制邏輯模塊主要包含燃料量控制算法和優選環節，用于接收燃氣輪機模型提供的監測信號，計算出燃料量，并經優選環節將燃料量反饋給燃氣輪機模型。為消除燃料量初始值對數字仿真模型迭代結果的影響，對燃料量進行最小值限制，保證數字仿真模型迭代計算的準確性。

1.2.1 燃料量控制算法

由于PID 控制是最早實用化的控制算法，現在仍然是控制系統中應用最為普遍的一種控制規律。它所涉及的算法和控制結構簡單，實際經驗以及理論分析都表明，這種控制規律對許多工業過程進行控制時，一般都能得到較為滿意的控制效果[14]。因此本文采用PID 控制調控燃料量實現燃氣輪機的轉速控制。

燃料量控制采用比例積分運算（PI 控制），與傳統的積分環節不同，本文采用可變積分增益系數進行積分環節的構建。

式中：Wfx為燃料量差值，x為代入的不同控制變量；KP為比例增益系數；KI為積分增益系數；?為限制條件值或控制變量的目標值與當前狀態值的偏差；Wf為經優選環節后反饋的燃料增量；τ為已運行的控制邏輯運算次數。

1.2.2 優選環節

如圖2 所示，燃料量調節輸出的優選環節采用最小值選取原則，具體包含4 個控制變量，分別為燃氣發生器轉速調節（PID_GG）、壓氣機出口壓力安全控制燃料量限制（PID_P3）、壓氣機出口溫度安全控制燃料量限制（PID_T3）、最大燃料量限制（PID_WMAX），其中燃氣發生器轉速為主控制變量，其余3 路為限制條件，保證所選取的燃料量滿足燃氣輪機運行需求。

圖 2 燃料量優選邏輯Fig. 2 Fuel quantity optimization logic

1.3 監測信號遲滯模型

為達到監測信號每隔一定時間傳輸一次真實數據的遲滯效果，在監測信號輸出模塊之后增加零階保持模塊，并補充速率轉換模塊，保證采樣時間一致。零階保持模塊的采樣時間為遲滯時間，可根據需求設置為0.1 s 和0.2 s 等。

零階保持模塊是一種按照恒指規律外推的保持模塊，具有將當前采樣時刻的信號值保持到下一個采樣時刻的功能。其原理如下式：

式中：T為遲滯時間；t為采樣時刻；U(t)為當前采樣時刻的信號值；U(nT)為上一采樣時刻的信號值。

2 監測信號遲滯的影響分析

2.1 調節時間

調節時間是反映控制系統響應速度的指標。其定義為控制系統受到外界擾動作用后，被控變量由之前的穩定狀態轉變到新的穩定狀態所經歷的最短時間。理論上調節時間為無限長，在實際應用中，只要被控變量進入新的穩態值±5%或±2%范圍內，且不在超出該范圍時所需的最短時間作為該控制系統的調節時間。

調節時間的計算方式如下式：

式中：tS為調節時間；t2為被控變量由初始平衡態到達新的平衡態的時刻；t1為被控變量初始平衡態向新的平衡態轉變的時刻。

2.2 轉速遲滯的影響

為獲得轉速遲滯對燃氣輪機轉速控制的影響，以轉速遲滯時間T_GG為變量進行計算，計算結果如圖3 所示。可知，隨著T_GG的增大轉速控制呈現2 種特性。轉速曲線的階梯式變化趨勢更為明顯，到達目標轉速的調節時間逐漸增長。另一方面，轉速曲線隨T_GG增大時所呈現的階梯式變化趨勢，表明監測信號遲滯模型具有良好的監測信號遲滯的復現能力，為研究監測信號遲滯對轉速控制的影響提供了必要保證。

圖 3 存在轉速遲滯的轉速曲線Fig. 3 Speed curve with speed hysteresis

由于存在轉速遲滯時，轉速控制所呈現的特性均會嚴重影響燃氣輪機正常運行。如圖4 所示，與無遲滯的燃料量曲線相比，存在轉速遲滯時燃料量曲線產生了不同程度的振蕩，且T_GG越小振蕩越明顯。這種燃料量劇烈波動的情況在實際運行過程中所引起的轉速波動遠大于數字仿真所展示的現象。

圖 4 存在轉速遲滯的燃料量曲線Fig. 4 Fuel quantity curve with speed hysteresis

當轉速存在遲滯時，每個遲滯周期的轉速為恒定值，此時轉速調節可以看成存在多次階躍的轉速調節。每次階躍均需要進行燃料量調節，以保證所供應的燃料量滿足轉速需求。如圖5 所示，當T_GG較小時，轉速控制階躍次數多、間隔時間短、且由于積分項的耦合作用，導致燃料量調節輸出振蕩，燃料量優選環節混亂，燃料量波動大且供應不足，使得燃氣發生器轉速未能到達調節目標。

圖 5 T_GG=0.2 s 的燃料量調節輸出Fig. 5 Fuel quantity regulation output with T_GG=0.2 s

隨著T_GG的增大，轉速階躍次數減少，間隔時間增大，燃料量優選環節趨于正常，燃料量趨于穩定，使得燃氣發生器轉速趨于調節目標。因此對轉速信號的采集上傳時間應該嚴格要求，且應嚴格控制在100 ms 以內。

2.3 壓力遲滯的影響

為獲得壓力遲滯對轉速控制的影響，以壓力遲滯時間T_P3 為變量進行計算，計算結果如圖6 所示。由圖6(a)可知，隨著T_P3 的增大，燃氣發生器轉速的穩態值逐漸減小；由圖6(b)可知，調節時間與T_P3 成正比例關系，且T_P3 小于0.2 s 時，調節時間與無遲滯時的調節時間接近，因此壓力遲滯應嚴格控制在200 ms以內。

圖 6 存在壓力遲滯的轉速曲線和調節時間曲線Fig. 6 Speed curve and regulation time curve with pressure hysteresis

如圖7 所示，與無遲滯的燃料量調節輸出曲線相比，存在遲滯的燃料量調節輸出曲線呈現出階梯式變化趨勢。產生階梯式變化趨勢的原因在于，燃料量優選結果在PID_P3 和PID_WMAX 之間交替變換，導致燃料量計算值偏小，燃氣發生器轉速升速減緩，調節時間增長。

圖 7 存在壓力遲滯的燃料量調節輸出Fig. 7 Fuel quantity regulation output with pressure hysteresis

2.4 溫度遲滯的影響

為獲得溫度遲滯對轉速控制的影響，以溫度遲滯時間T_T3 為變量進行計算，計算結果如圖8 所示。由圖8(a)可知，隨著T_T3 的增大，轉速曲線基本重合；由圖8(b)可知，無論T_T3 如何變化，調節時間無明顯改變，因此溫度遲滯對轉速控制的影響較小。

圖 8 存在溫度遲滯的轉速曲線和調節時間曲線Fig. 8 Speed curve and regulation time curve with temperature hysteresis

如圖9 所示，與無遲滯的燃料量調節輸出曲線相比，存在溫度遲滯時，僅有PID_T3 呈現階梯式變化趨勢，且并未改變燃料量優選結果，由此可見，溫度遲滯對轉速控制的影響極小。

圖 9 存在溫度遲滯的燃料量調節輸出Fig. 9 fuel quantity regulation output with temperature hysteresis

3 控制參數與壓力遲滯耦合分析

3.1 壓力遲滯與比例增益系數耦合的影響

為獲得壓力遲滯與比例增益系數KP耦合對轉速控制的影響，選取變量為T_P3 和KP，計算結果如圖10 所示。可知，轉速控制存在2 個特性。調節時間與KP成反比例關系，且KP大于0.5 時，調節時間趨于恒定值；隨著T_P3 的增大，增大KP對調節時間的影響減弱。

圖 10 T_P3 和KP 耦合時的調節時間曲線Fig. 10 Adjustment time curve when T_P3 and KP are coupled

為探究T_P3 和KP耦合時對轉速控制產生前述影響的原因，從燃氣發生器轉速和燃料量調節輸出的角度進行分析，如圖11 和圖12 所示。

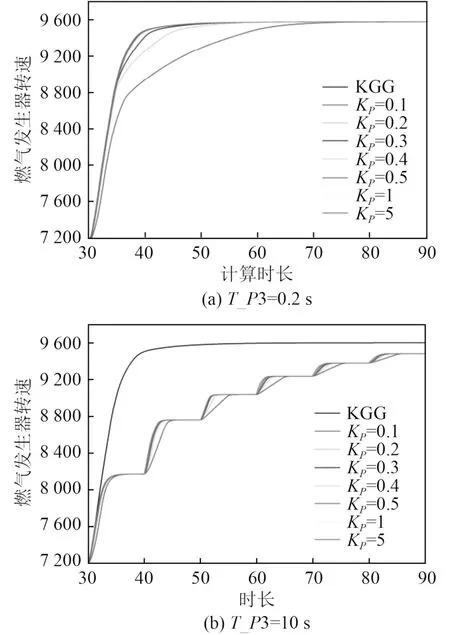
圖 11 固定T_P3 且改變KP 時的轉速曲線Fig. 11 Speed curve when fixing T_P3 and changing KP

圖 12 T_P3 和KP 耦合時的燃料量調節輸出Fig. 12 Fuel quantity regulation output when T_P3 and KP are coupled

1）首先從保持T_P3 恒定，改變KP的角度進行分析：由圖11 可知，隨著KP的增大，燃氣發生器轉速趨近于無遲滯時的轉速；由圖12 可知，隨著KP的增大，燃料量調節輸出增大，燃料量優選結果由PID_P3 逐漸轉變為PID_GG 和PID_WMAX 之間交替選擇，使得轉速控制效果更佳，燃氣發生器轉速趨于調節目標，調節時間減小。

2）結合壓力遲滯對轉速控制的影響規律，對T_P3 和KP耦合時轉速控制的變化趨勢展開分析。當T_P3 較小時，燃料量調節輸出雖然存在波動，但其對燃料量優選結果的干擾較小，KP大于0.4 時轉速曲線與無遲滯的轉速曲線基本重合，與圖6(a)中T_P3=0.2 s時的轉速曲線相比，增大KP可以提升轉速控制性能；當T_P3 較大時，受壓力遲滯的影響，燃料量調節輸出的階梯式變化極為明顯，對燃料量優選結果的干擾較大，燃料供應不足，調節時間增大，且增大KP基本無變化。

綜上所述，當燃氣輪機存在壓力遲滯現象時，可通過增大KP的途徑提升轉速控制性能；當T_P3 較小時，增大KP對轉速控制性能的提升較為明顯；當T_P3 較大時，增大KP對轉速控制性能無明顯提升。

3.2 壓力遲滯與積分增益系數耦合的影響

為獲得壓力遲滯與積分增益系數KI耦合對轉速控制的影響，所選取變量為T_P3 和KI，計算結果如圖13所示。可知，轉速控制存在2 個特性：調節時間與KI成正比關系，且KI小于0.95 時，調節時間趨于恒定值；隨著T_P3 的增大，改變KI對調節時間影響減弱。

圖 13 T_P3 與KI 耦合時的調節時間曲線Fig. 13 Adjustment time curve when T_P3 and KI are coupled

為探究T_P3 和KI耦合時對轉速控制產生前述影響的原因，采用與T_P3 和KP耦合影響相同的分析方法進行分析，如圖14 和圖15 所示。分析結果如下：

圖 14 固定T_P3 且改變KI 時的轉速曲線Fig. 14 Speed curve when fixing T_P3 and changing KI

圖 15 T_P3 和KI 耦合時的燃料量調節輸出Fig. 15 Fuel quantity regulation output when T_P3 and KI are coupled

與KP對轉速控制的影響原因基本一致，主要表現為：隨著KI的減小燃料量調節輸出增大，燃料量優選結果由PID_P3 逐漸轉變為PID_GG 和PID_WMAX 之間交替選擇，且更加接近無遲滯時的優選結果，使得燃氣輪機轉速控制效果更佳，轉速升速率增大，調節時間減小；當T_P3 較小時，減小KI有利于提升轉速控制性能；當T_P3 較大時，減小KI的對轉速控制基本無影響。

4 結 語

通過Matlab/Simulink 建立具有監測信號遲滯功能的數字仿真系統，進行轉速遲滯、壓力遲滯和溫度遲滯對燃氣輪機轉速控制效果的影響及PID 控制參數與監測信號遲滯耦合對燃氣輪機轉速控制的影響研究。所得結論如下：

1）轉速遲滯和壓力遲滯是燃氣輪機轉速控制的主要影響因素，且轉速遲滯的影響大于壓力遲滯，溫度遲滯對燃氣輪機轉速控制無影響；

2）為提升燃氣輪機轉速控制的可靠性和穩定性，轉速遲滯時間應控制在100 毫秒級以內，壓力遲滯時間應控制在200 毫秒級以內；

3）在監測信號遲滯較小時，增大比例增益系數KP和減小積分增益系數KI有利于提升燃氣輪機轉速控制性能，但隨著監測信號遲滯時間的增大，改變PID 控制參數對燃氣輪機轉速控制性能的提升效果逐漸減弱，甚至消失。