“三招”學好冪的運算性質

康海芯

冪的運算性質是整式乘法運算的重點內容之一，也是學習的難點。為幫助同學們學好冪的運算性質，本文將從三個方面加以分析，供同學們學習時參考。

一、明確不同類型冪的運算性質的相同點與不同點

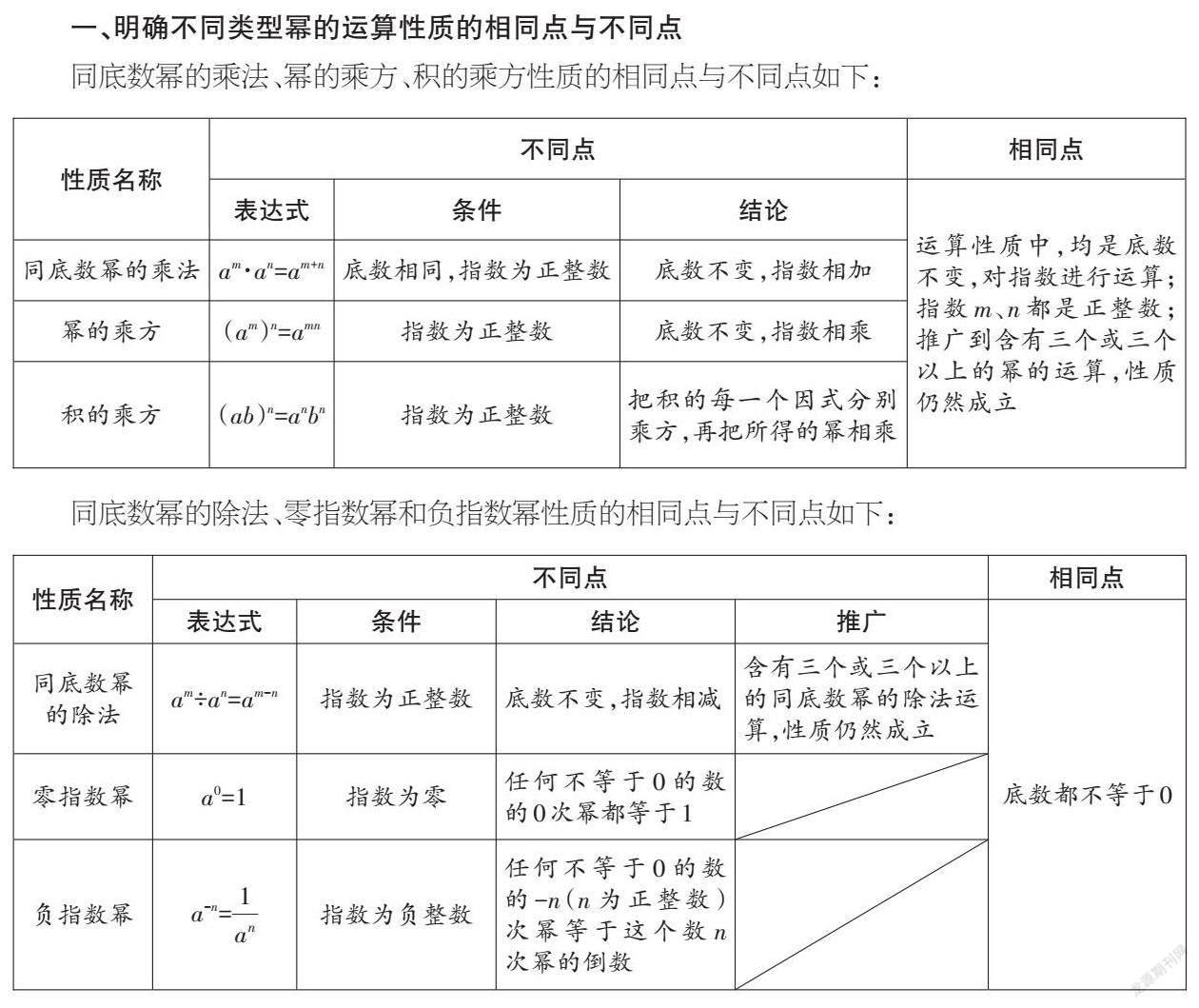
同底數冪的乘法、冪的乘方、積的乘方性質的相同點與不同點如下：

同底數冪的除法、零指數冪和負指數冪性質的相同點與不同點如下：

二、領悟冪的運算性質中字母的內涵

同底數冪的乘法、冪的乘方中的字母a，積的乘方中的字母a、b，既可以表示任意的數，也可以表示單項式或多項式；在同底數冪的除法、零指數冪或負指數冪的運算性質中，底數可以是不等于0的單項式，也可以是不等于0的多項式。底數是多項式時，應看作一個整體。

如計算（x-y）·［（x-y）3］3·（x-y）2，通常把（x-y）看作底數，先運用冪的乘方性質，然后運用同底數冪的乘法運算性質進行計算，可以得到（x-y）·（x-y）9·（x-y）2=（x-y）12。

三、遠離冪的運算中“想當然”的錯誤

學習冪的運算性質時，我們首先應該弄清楚每個運算性質的產生或推導過程，不能只是被動地記憶公式。被動地記憶，我們只能記住它的外形，不能理解性質的本質，當出現與外形類似的公式時，容易與其他性質相互混淆而出現錯誤。

例如，計算（m-n）3·（n-m）2，許多同學容易出現“原式=（m-n）3·［-（m-n）2］=-（m-n）5”這樣的錯誤。（n-m）2的底數（n-m）換成-（m-n）時，全式應該換成［-（m-n）］2，而不應該等于-（m-n）2。我們把（x-y）n（n為正整數）化成底數為（y-x）的式子時，要根據指數n的奇偶性來判斷結果。當n為奇數時，（x-y）n=-（y-x）n；當n為偶數時，（x-y）n=（y-x）n。

其次，我們在運算時，要“識別”每道題運算的類型，包括符號、字母和指數，“聯想”到對應的運算性質，尤其要注意領悟不同類型的冪的運算的區別與聯系，避免出現不加思考、隨意套用運算法則的情形。……