局部頻率測量數據驅動的電力系統功率缺額在線評估方法

唐 震, 郝麗花, 馮 靜

(1. 國網山西省電力公司 電力科學研究院,太原 030001; 2. 中國電力科學研究院有限公司,北京 100192)

維持系統頻率穩定是保障電力系統安全穩定運行的重要前提,其本質是保持系統有功功率實時平衡[1].然而在新型電力系統中,可再生能源滲透率不斷增加,一方面由于以電力電子器件為接口的新能源發電替代了一部分以同步發電機為主的常規電源,使得系統慣量水平顯著降低[2-3];另一方面,新能源發電具有較大的不確定性,在系統動態過程中極易產生較大的功率缺額,從而導致頻率偏移超出安全范圍,嚴重威脅系統頻率穩定[4].

新型電力系統具有較低慣量,受到擾動而產生較大功率缺額時系統頻率會快速下降,從擾動開始至頻率下降到最低點所需時間極短,一般為幾秒鐘.因此需要在產生功率缺額后的幾秒鐘內采取相應的控制措施,快速注入所缺功率,以維持頻率在安全范圍內.但由于同步發電機受機械約束條件限制,其響應速率已無法滿足新型電力系統頻率穩定性要求.隨著電力電子設備、現代通信技術和同步測量技術的快速發展,新型調頻手段逐漸成熟,為解決上述難題提供了技術支撐[5-7].例如,在電力系統發生較大功率缺額時,一方面可以利用風力機和光伏發電的頻率控制技術,在低頻事件下釋放備用功率;另一方面可以利用儲能系統響應速度快、跟蹤功率能力強等優點,快速控制雙向功率.利用電力電子器件的快速響應能力可以有效減少新型電力系統擾動后的功率缺額.因此,快速和準確評估功率缺額是增強新型電力系統頻率穩定性的重要前提.

同步測量技術在電力系統的廣泛應用為實時監測頻率變化情況提供了現實基礎,大批學者圍繞系統功率缺額評估方法展開了深入研究.例如,文獻[8]在汽輪機經典發電機模型下,推導得到電力系統頻率變化率與有功功率缺額之間的數學關系,該方法利用擾動發生時刻的慣量中心(Center of Inertia, COI)頻率變化率計算系統功率缺額,但未討論COI頻率變化率的獲取方法.文獻[9]采用了非遞歸牛頓型算法對各臺同步發電機頻率進行濾波處理,得到較為精確的系統COI頻率,從而在發電機慣量已知的前提下,基于轉子運動方程計算得到系統的功率缺額值.文獻[10-11]在此基礎上考慮了擾動初期電壓偏移對負荷有功變化的影響,提出一種計及負荷靜態模型的功率缺額計算方法.

然而,上述基于數學模型的功率缺額評估方法存在以下兩方面問題:① 上述方法中,獲得系統COI頻率需要通過多個相量測量單元(Phase Measurement Units, PMUs)同步測量每臺發電機的頻率,并進行廣域通信,因此存在可靠性差、通信延遲等問題;② 這些方法都是在系統慣量和擾動發生時刻已知的情況下對功率缺額進行評估,然而在新型電力系統中,系統慣性常數呈現復雜的非線性時變特征,實時慣量難以獲取.盡管近年來許多學者[12-14]結合負荷側和發電機側信息在系統慣量實時評估方面開展了大量研究,但仍存在過于依賴精細化模型和適應性差等問題.

因此,針對問題①,本文提出了一種無需通信的系統COI頻率估算方法,僅需測量局部頻率信息,即可近似得到系統的COI頻率曲線,且精度與基于同步測量的方法相當,有效避免了通信延遲,提高了系統功率缺額的評估速度.此外,隨著人工智能技術的快速發展,深度學習方法已經成為開展電力系統領域預測分析的有力工具.在此基礎上,針對問題②,考慮深度卷積神經網絡(Deep Convolutional Neural Network,DCNN)能夠充分捕獲鄰近時間點的頻率信息、長短期記憶(Long-Short Term Memory,LSTM)網絡可充分挖掘全時間段頻率數據之間隱含的時序關系,提出一種新的基于DCNN-LSTM復合神經網絡模型的電力系統功率缺額評估方法.該方法無需預知系統慣性常數及建立復雜的數學模型,利用DCNN和LSTM充分挖掘連續時間點的頻率數據與功率缺額間的關聯信息,從而實現快速和準確評估電力系統功率缺額.

1 基于局部頻率測量的電力系統COI頻率估算方法

在發生擾動后,電力系統的頻率響應將依次經歷慣量響應、一次響應和二次響應3個階段[15].慣量響應一般體現在擾動發生后的短暫時刻,同步發電機儲存的旋轉動能將自發釋放,維持功率平衡,從而降低系統頻率變化率.

單臺同步發電機的旋轉動能通常被歸一化為慣性常數H,定義為額定轉速下儲存的旋轉動能與同步發電機額定容量的比值,即

(1)

式中:EG為發電機旋轉動能;S為發電機的額定容量;J為轉動慣量;wm為發電機額定轉速.

對于包含M臺互聯同步發電機的大型電力系統,根據系統整體慣量守恒,將所有具有慣性貢獻的發電機等效為一臺同步發電機,則系統的等效慣性常數可以表述為

(2)

式中:Hi、Si分別為第i臺發電機的慣性常數、額定視在功率.

同步發電機的轉子運動方程表示當系統發生擾動導致同步發電機機械功率和電磁功率不平衡時,轉子轉速的動態變化及頻率偏移與功率不平衡之間的關系,可廣泛應用于基于暫態頻率的功率缺額評估以及頻率控制的設計和調節等,表示如下:

(3)

式中:δ為同步發電機的功角;f為測量得到的發電機頻率;fm為發電機額定頻率;Pm、Pe分別為同步發電機的機械功率和電磁功率;df/dt為發電機頻率的時間變化率.

由式(2)、(3)可知,通過對擾動后系統頻率變化率進行準確測量或者估計,可以計算得到系統發生擾動時的功率缺額.

然而對于大型電力系統來講,在暫態過程中,各機組轉速各不相同,導致在不同母線測得的頻率也不相同[16].因此,通常使用慣性中心頻率變化來描述系統頻率響應過程,其表達式為

(4)

式中:fi為第i臺發電機的頻率.由式(4)可知,要計算得到電力系統的COI頻率變化曲線,不僅需要同步測量系統中每臺發電機的頻率,還需要可靠的通信網絡將測量到的各個頻率傳送到控制中心.由于存在通信延遲和測量誤差,所以此種COI頻率計算方法難以用于實時在線評估.

因此,提出一種無需通信的擾動后系統COI頻率估計方法.該方法可以實現在不需要廣域頻率監測的情況下,僅基于測量的某臺發電機頻率來估算得到系統COI的頻率變化曲線.具體說明如下:對于經典的兩機系統,可近似將每臺發電機以一等值電抗和該電抗后的電動勢來代表,負荷為恒定阻抗,其網絡模型如圖1所示.圖中:X表示發電機的等值電抗;R表示發電機的等值電阻;U1、U2為兩臺同步發電機的內電勢幅值;δ1、δ2為兩臺同步發電機的功角.

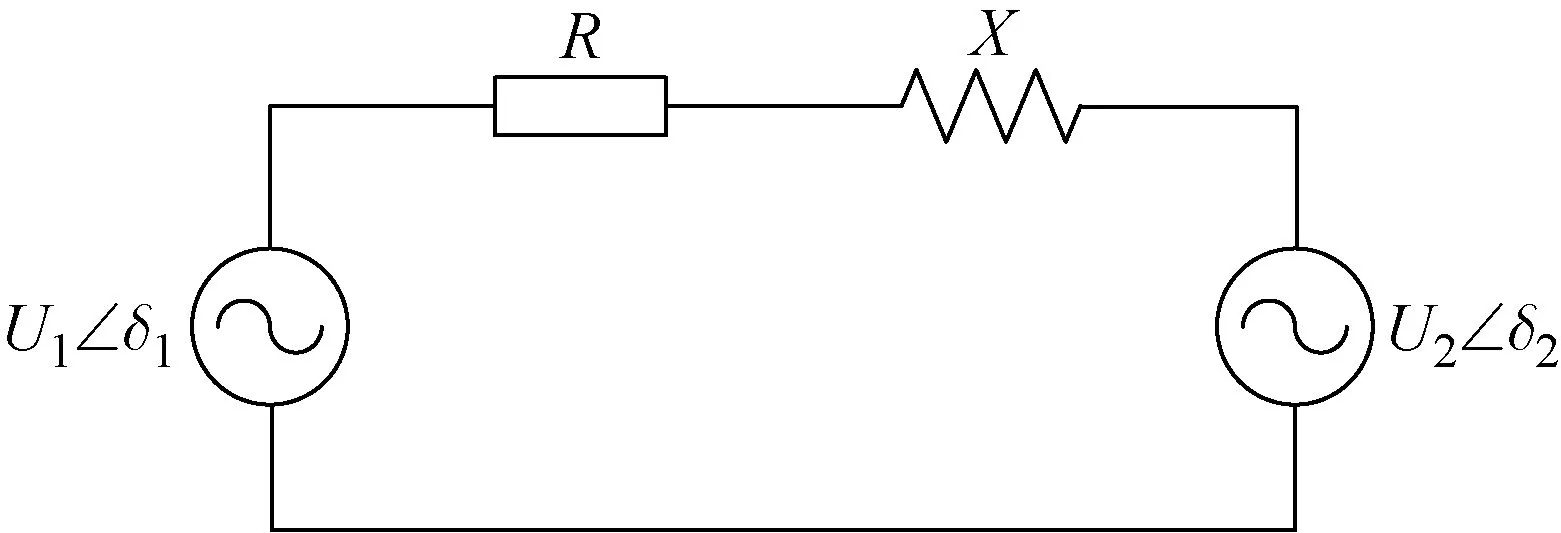
圖1 經典兩機系統模型圖

兩臺發電機的功率特性分別為

(5)

式中:Pe1、Pe2分別為兩臺發電機的電磁功率;Y12為兩臺發電機電動勢之間的互導納(G12+jB12),G12和B12分別為兩臺發電機間的電導與電納;|Y12|為Y12的模值;G11、G22為節點1、2的自電導;δ12為兩臺發電機之間的轉子角差值,即δ1-δ2;β12=arctan(G12/B12).

由于發電機的機械功率在擾動發生后的短時間內是不變的,因此將式(2)關于時間t求微分可得:

(6)

結合式(5)可得:

(7)

由式(3)、(7)可知,當發電機頻率對時間的二階導數變為0,此時f1=f2=fCOI,即各臺發電機頻率相同,測量點發電機頻率的拐點恰好位于COI頻率曲線上.因此可以利用該性質,將測量點頻率的拐點依次相連,得到的分段線性曲線可以近似代替兩機系統的COI頻率變化曲線, 如圖2所示.圖中:SG1表示發電機1;p.u. 表示標幺值.

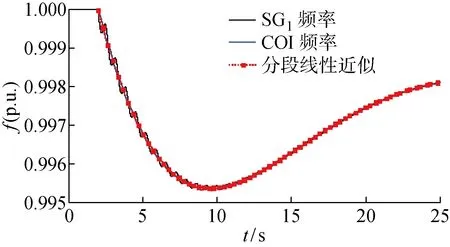
圖2 兩機系統受擾后的頻率響應

通過對實際多機系統的大量數值仿真實驗可以看出,將上述兩機系統推導得到的性質應用在多機系統中,所得到的分段線性近似頻率曲線與測量得到的COI頻率曲線依然近似相等.

2 基于DCNN-LSTM的電力系統功率缺額評估模型

針對系統頻率與功率缺額之間的數學關系過于復雜(高階非線性方程)且計算量過大等問題,提出一種基于DCNN-LSTM的電力系統功率缺額評估方法,提高模型的估算速度和精度,實驗具體過程如圖3所示.

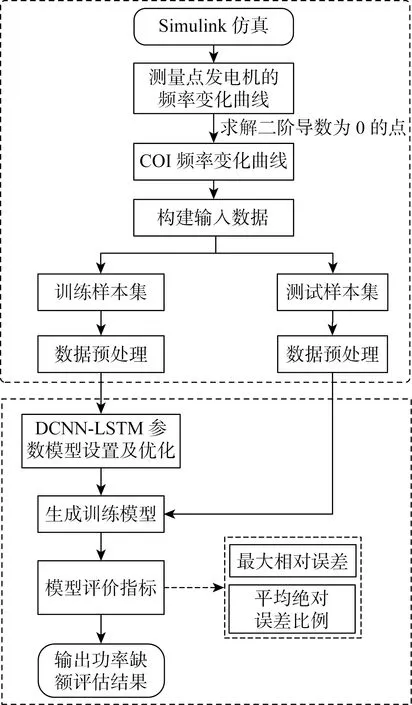
圖3 基于DCNN-LSTM的電力系統功率缺額建模過程

2.1 實驗流程與仿真模型介紹

試驗在Intel(R)Core(TM)i5-1135G7 CPU @ 2.40 GHz的Inter Corporation環境上運行,使用Python3.6編譯環境,并采用tensorflow2.8的深度學習架構.共計 2 000 組有效數據,并將其按9∶1的比例分為訓練樣本集和測試樣本集,其中 1 800 組數據作為訓練集,輸入到DCNN-LSTM訓練模型中進行訓練,另外200組作為測試集驗證模型,從而進行系統功率缺額評估.

利用同步發電機原理進行IEEE-39節點系統仿真得到實驗數據集,仿真環境為MATLAB/Simulink.該系統是新英格蘭地區高壓輸電系統的簡化模型,網絡結構如圖4所示.其中發電機1是外部電網等效發電機,發電機2是平衡發電機,且發電機2～10采用自動調壓器和調速器,WT1、WT2、WT3為3臺風力發電機組,BESS1、BESS2為兩個儲能系統,PV1、PV2為兩臺太陽能光伏發電機組.當系統發生較大擾動產生功率缺額后,WT、PV及BESS可以迅速釋放有功功率,以維持頻率穩定性.

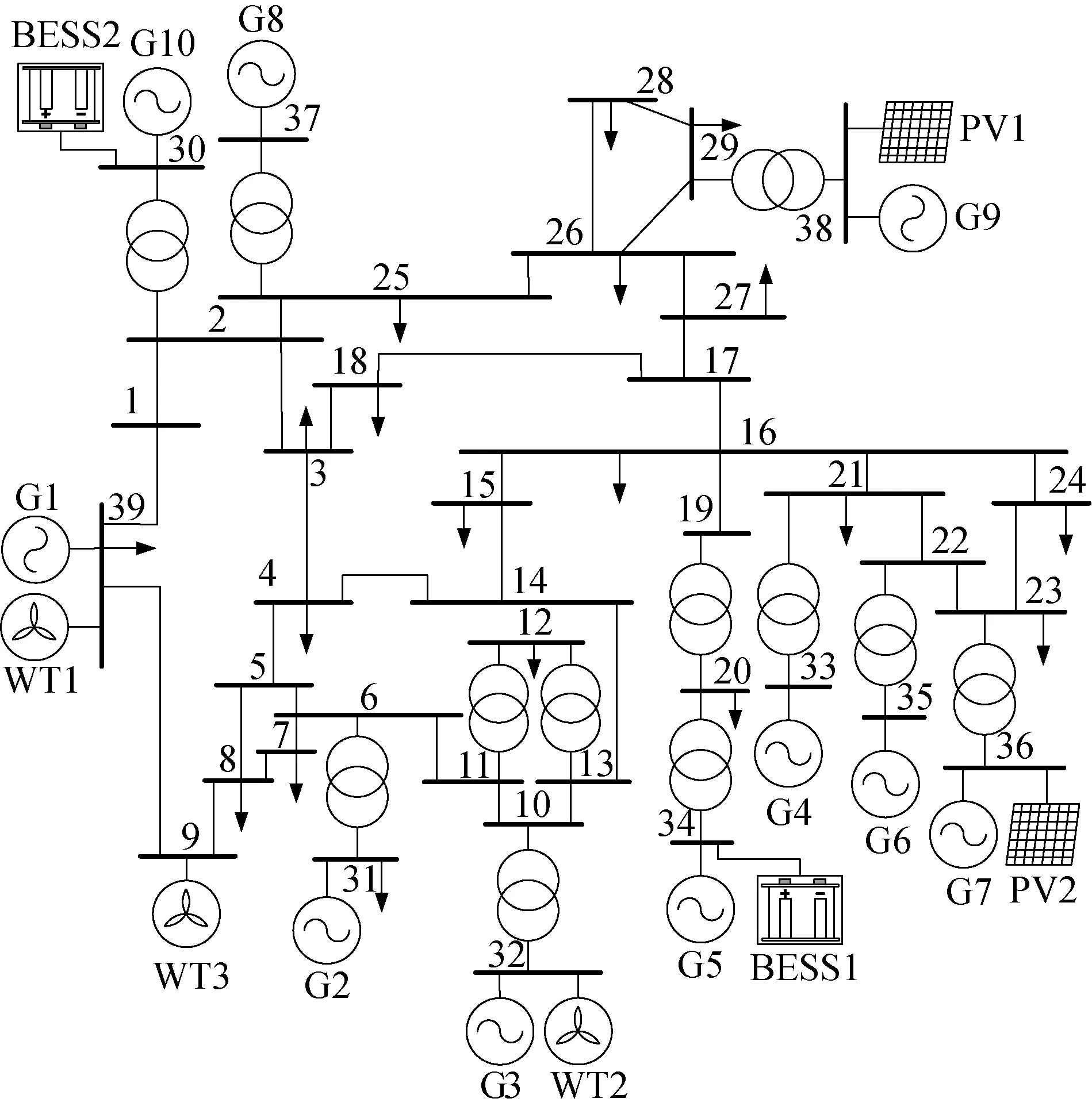
圖4 新英格蘭10機39節點測試系統

2.2 樣本數據集的構建及預處理

系統功率缺額評估需要構建科學合理的特征量作為樣本數據集.首先通過改變仿真系統中功率缺額的大小,并基于廣域測量技術得到測量點某臺發電機的頻率變化情況;然后基于式(3)～(7)推導得到的性質,運用有限差分法求解離散數據二階導數為0的點,并將這些拐點依次相連,估算得到系統COI頻率變化曲線;此外,每隔0.1 s對COI頻率變化數據采樣一次,得到50組具有相同時間間隔的頻率變化數據,從而構建一組尺寸大小為50×1的原始輸入特征數據,而其對應的輸出層標簽為改變的系統功率缺額值;最后,通過改變系統功率缺額的大小和測量點發電機的標號,反復進行 2 000 次實驗得到相應的 2 000 組有效數據,從而構建得到一維輸入數據樣本集.

系統COI頻率變化數據的差異分布范圍很大,因此需要對其進行數據預處理,即采用數據歸一化的方法,將輸入數據的特征映射到[0, 1]區間,從而達到提高訓練效率及評估精度的目的[17].其數學表達式為

(8)

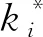
2.3 DCNN-LSTM模型架構設計

為了從上述構建的具有時間序列特征的頻率測量數據樣本中提取關鍵信息,首先采用多個CNN卷積核形成多個特征提取器,使用了大小為1×5的卷積核以充分捕捉鄰近幾個時間點的頻率關聯信息,如頻率的變化率、拐點等.因此,卷積神經網絡是從整體長時間序列的較短頻率片段中提取有效的關聯特征,其傳播過程可參考文獻[18].

由于所輸入的頻率數據在時間維度上存在整體相關性,所以在功率缺額預測過程中,僅依靠CNN模型難以捕獲全時間段的關聯信息.考慮到遞歸神經網絡LSTM的輸出不僅取決于當前的輸入值,而且還取決于在此之前的數據,即可以實現將時間序列作為一個整體輸入到網絡中進行訓練.因此將DCNN提取的特征傳輸到LSTM,利用LSTM來挖掘全時間段頻率數據之間的高度相關特性,從而提高功率缺額預測的準確性.LSTM的傳播過程可參考文獻[19].

設計一種用于在線精確評估擾動后功率缺額的DCNN-LSTM復合神經網絡架構,如圖5所示.所提DCNN-LSTM復合神經網絡架構的詳細參數如表1所示.

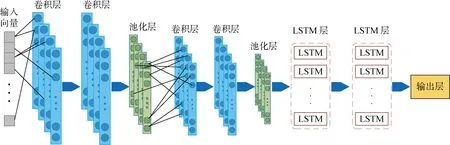
圖5 DCNN-LSTM網絡結構圖

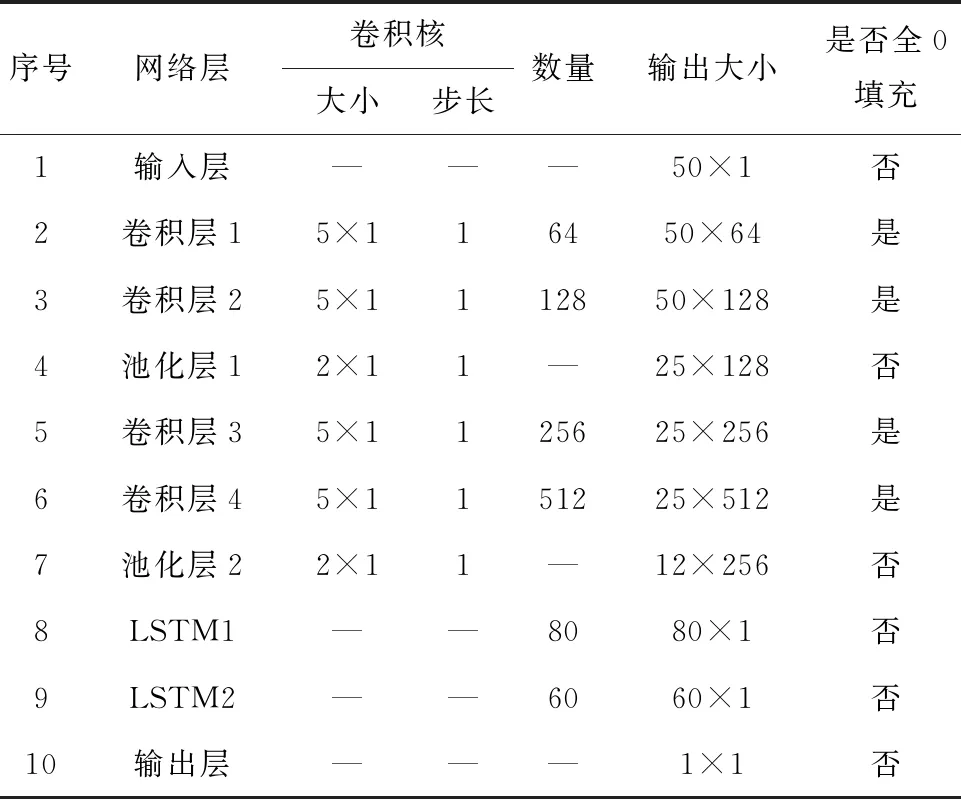
表1 DCNN-LSTM詳細參數

2.4 DCNN-LSTM模型訓練

在網絡的訓練過程中,損失函數的選擇對于衡量模型在訓練數據集上的性能至關重要.因此本文采用Huber損失函數,表達式如下:

(9)

式中:y為真實值;y′為模型的預測值.

為取得更好的計算效率,在模型訓練策略中采用Adam梯度下降法作為優化器[20].此外,使用批標準化和Dropout兩種方法消除神經網絡模型訓練過程中的過擬合現象,提升DCNN-LSTM復合神經網絡的泛化性能[21].

2.5 模型評價指標

為評估本文所提方法與CNN、LSTM等其他算法的預測準確性,算例仿真中選取平均絕對誤差百分比(Mean Absolute Percentage Error,MAPE)及最大相對誤差(Maximum Relative Error,MRE)作為預測效果的評價標準,表達式分別為

(10)

(11)

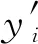
3 算例仿真分析

3.1 所提基于局部頻率測量數據的電力系統COI頻率估算方法的精度分析

本算例基于Simulink所構建的10機39節點系統,通過大量仿真實驗可以觀測到:由于系統內各發電機的機間存在機電振蕩模態,所以測量點發電機頻率圍繞系統COI頻率上下波動,且兩條頻率曲線的交點幾乎與發電機頻率曲線的拐點重合.因此將測量點發電機頻率的拐點依次相連所得到的分段線性近似COI頻率曲線與系統COI頻率曲線差別并不大,具體如圖6所示.

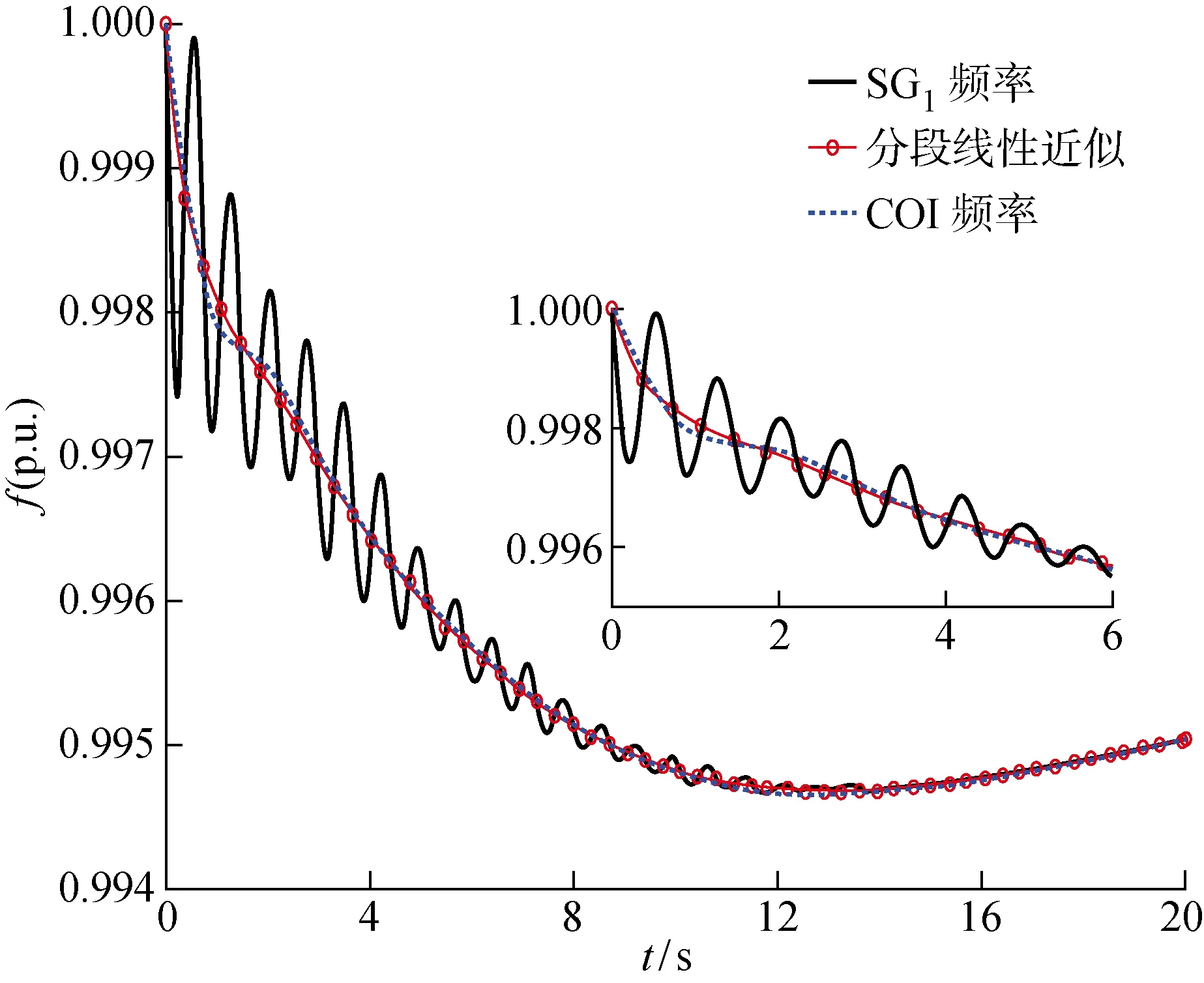
圖6 10機39節點系統受擾后的頻率響應

為了方便進行對比,對圖6差別相對較大的1～3 s內數據每隔0.1 s進行采樣,可得20組數據,分別編號1,2,…,20.進一步可得實際COI與近似COI頻率對比圖與頻率相對誤差變化圖,分別如圖 7(a)、7(b)所示.圖中:ER表示相對誤差.

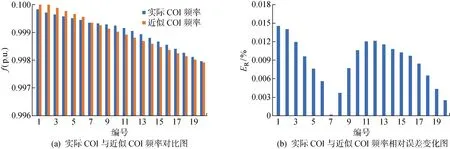
圖7 頻率誤差分析圖

由圖7可知,得到的近似COI頻率與實際COI頻率最大相對誤差為 0.014 5%,平均相對誤差為 0.008 7%.以上分析說明,將上述兩機系統推導得到的性質應用在多機系統中,所得到的分段線性近似COI頻率曲線具有很好的精確度,即與測量得到COI頻率曲線近似相等.同時,也從側面充分驗證了本文所提電力系統COI頻率估算方法具備無需廣域頻率監測技術的優勢,有效減少了對通信裝備的依賴度,為后文實現在秒級的時間尺度下快速評估功率缺額提供了技術支撐.

3.2 最優超參數下功率缺額評估情況

在表1所示網絡結構參數的基礎上,經過DCNN-LSTM模型訓練后,可得本文所提方法下測試集樣本數據的MAPE和MRE分別控制在2.74%和11.4%以內,預測值與實際值的偏差較小.其測試集樣本數據的誤差分布情況及系統功率缺額估算曲線和實測曲線對比情況,分別如圖8(a)、8(b)所示.圖中:N表示功率缺額的數值;N′表示測試集樣本數量;E表示誤差.

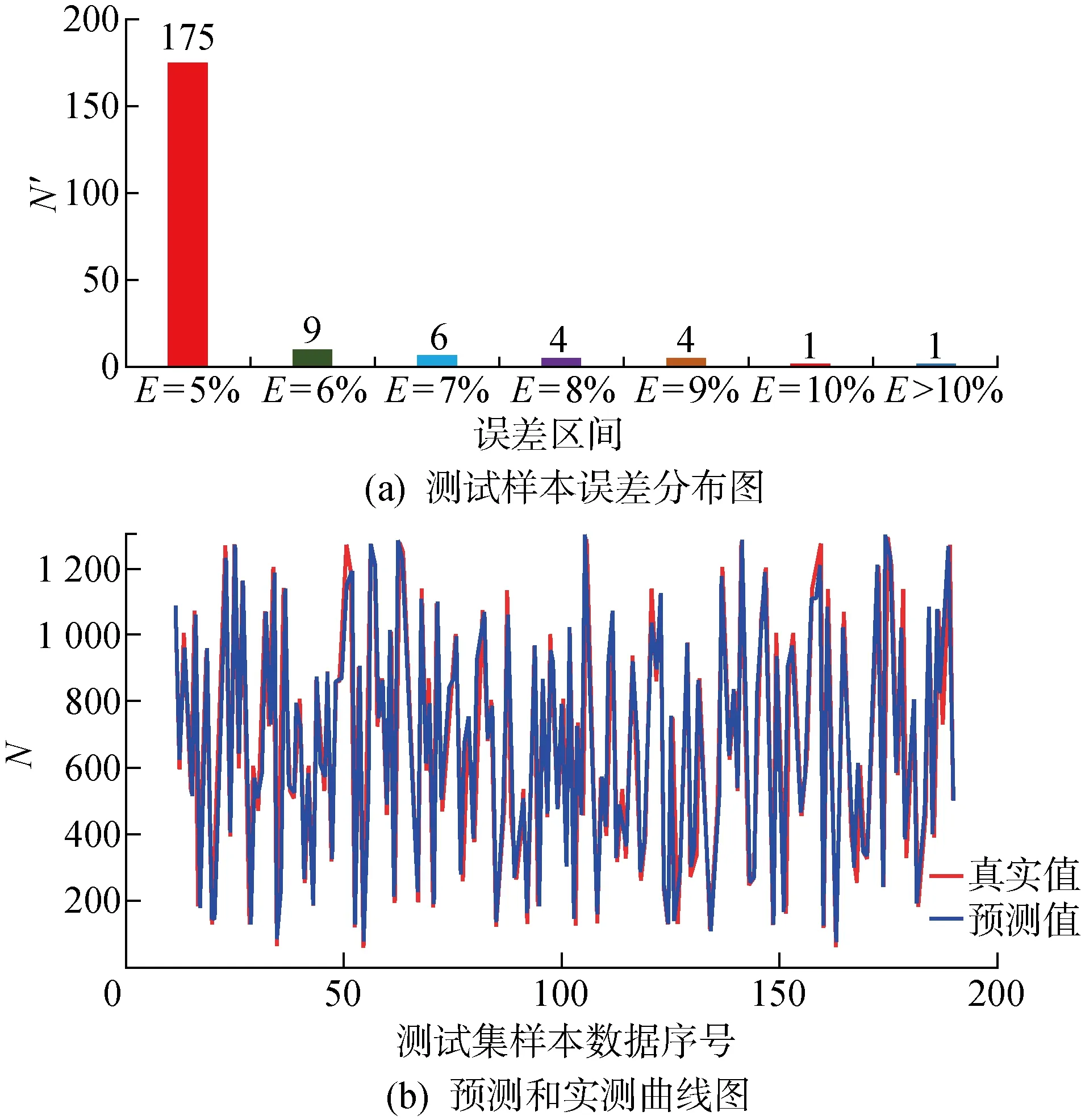
圖8 基于DCNN-LSTM的電力系統功率缺額評估結果

由圖8分析可知,200個測試樣本數據集中,87.5%以上的樣本數據控制在5%誤差以內,有99%測試樣本誤差保持在10%以內,因此所提方法可以準確評估擾動后的系統功率缺額.

3.3 不同系統功率缺額評估方法對比

根據式(2)可知,利用每臺同步發電機的慣性時間常數可計算得到電力系統的等值慣性常數,在此基礎上,結合式(3)以及系統COI頻率變化率即可計算得到系統擾動后的功率缺額[8],在此記該方法為方法1.因此對方法1、反向傳播(BP)、CNN、LSTM、CNN-LSTM等5種方法下測試集樣本數據的MAPE、最小相對誤差(NRE)、MRE、E、測試時間等各項評價指標進行對比分析,如表2所示.

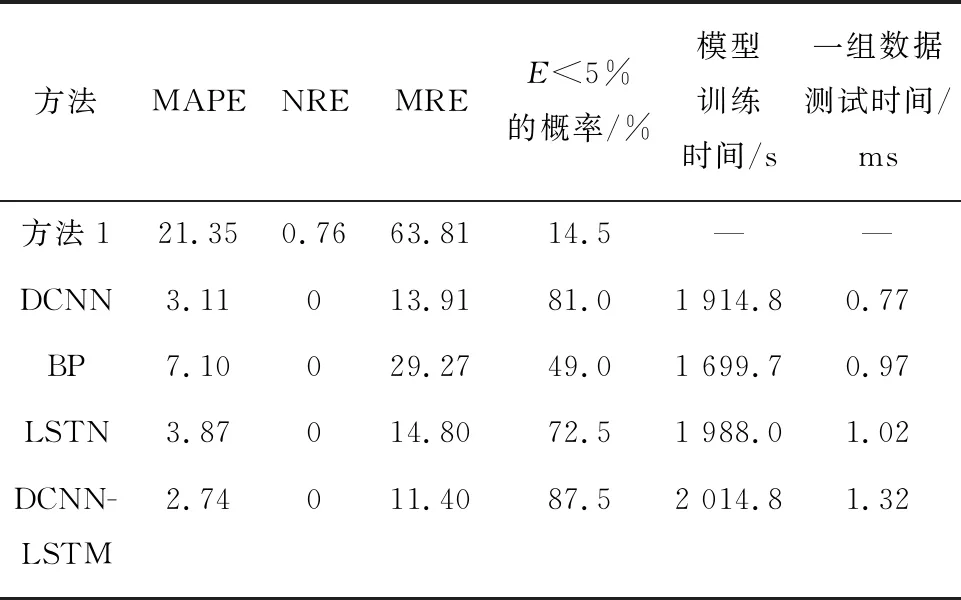
表2 不同方法下功率缺額評估結果

由表2可知,盡管DCNN-LSTM、BP等深度學習方法模型訓練時間均長達0.5 h左右,但在實際應用中,這些方法采用“離線訓練、在線預測”的框架,即在離線階段,策略模型使用梯度下降算法迭代更新深度神經網絡的參數,當模型經過訓練后,可實現快速在線計算.因此,DCNN-LSTM、BP等模型訓練時間上的巨大差異并不影響功率缺額的在線評估.此外,由于本文提出的利用局部測量頻率數據的COI頻率估算方法避免了廣域通信帶來的延時,可以較快獲取COI頻率,并且DCNN-LSTM預測時間僅為1.32 ms,可以完全滿足在線預測的速度要求,同時其預測精確度又高于其他方法,所以所提基于DCNN-LSTM的系統功率缺額方法能夠快速、準確地預測擾動后系統的功率缺額.

上述5種方法下測試集樣本數據的真實值y與預測值y′的分布情況、誤差區間分布情況分別如圖9、圖10所示.

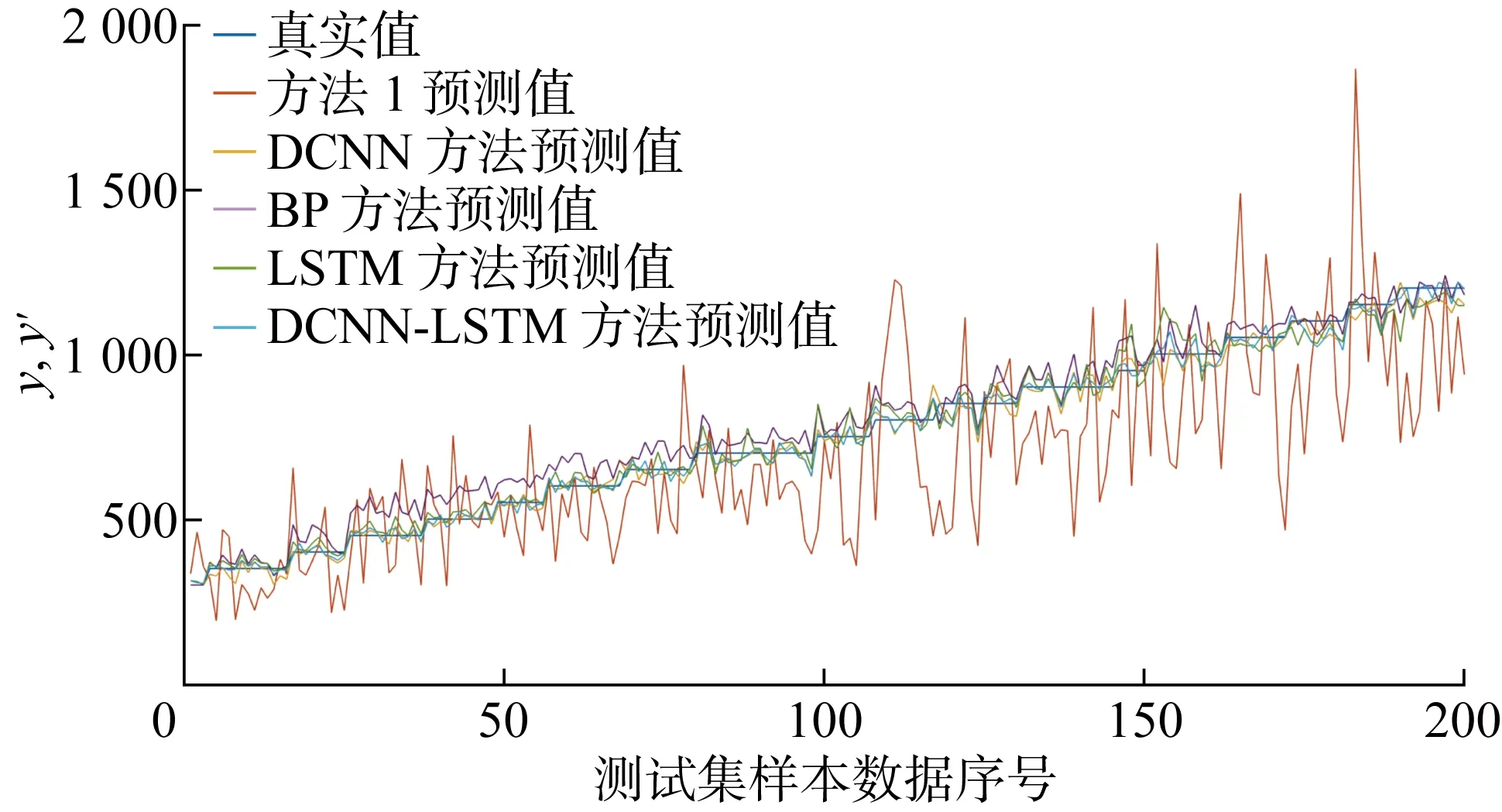
圖9 不同方法下的測試集數據真實值與預測值分布圖

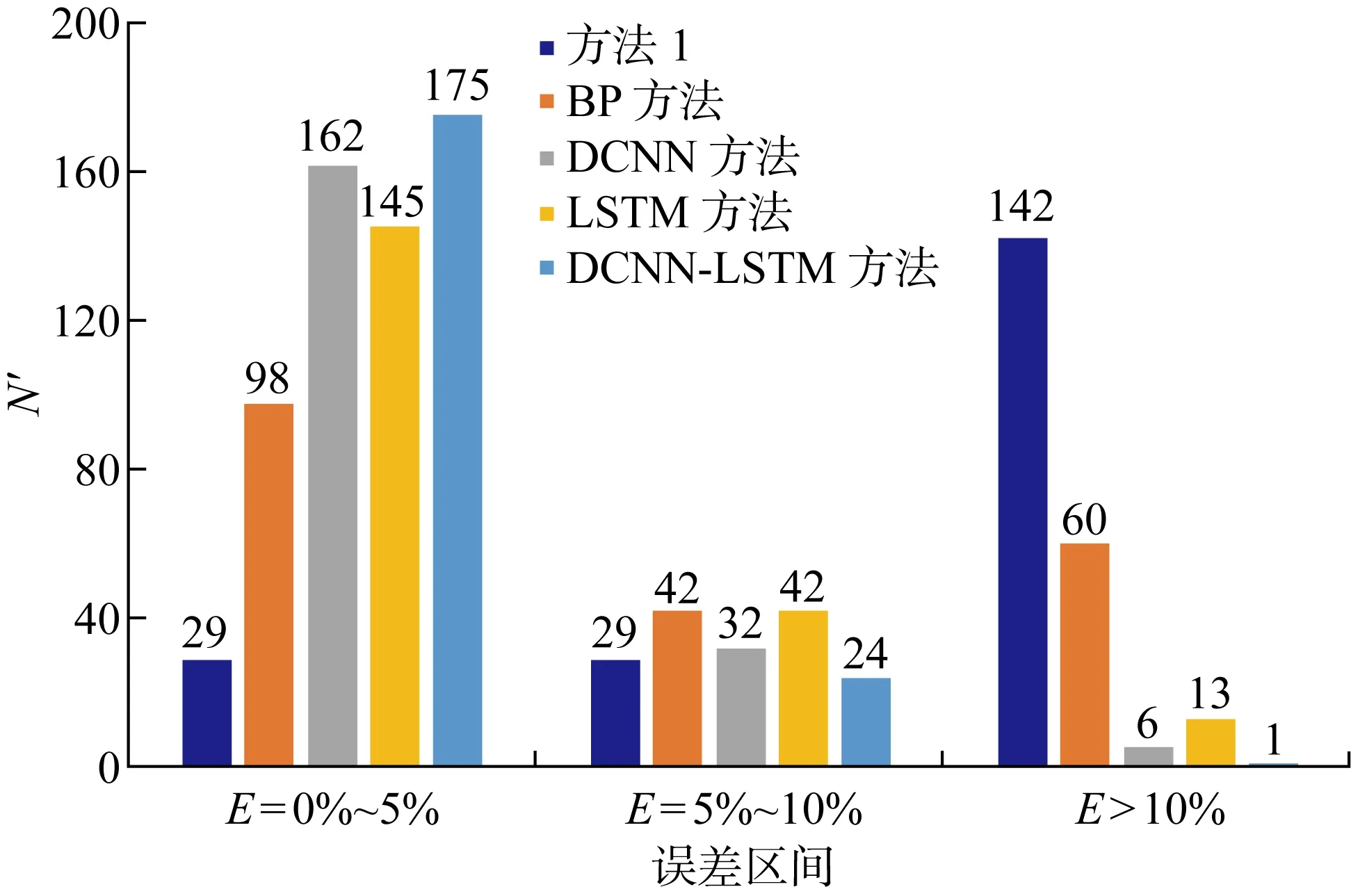
圖10 不同方法下的測試集數據誤差分布區間圖

由表2、圖9分析可知,方法1的評估結果與實際功率缺額值存在較大誤差,其主要因為方法1必須基于擾動發生初始時刻的頻率變化率以及系統實際的慣量常數,利用轉子運動方程計算得到有功功率缺額,然而在系統運行過程中通常具體擾動發生時刻未知,使得較難準確計算出擾動發生瞬間的頻率變化率;但基于數據驅動的人工智能算法,通過對系統COI頻率變化等輸入數據的提取,可以較為精確地預測到擾動后所需的有功功率缺額,從而更有助于電力系統運行人員在事故發生后采取適當的調頻措施.此外,結合圖10可知,DCNN-LSTM模型與DCNN、LSTM相比,樣本測試集誤差在5%以內的數據分別增多13、30個,誤差在10%以上的數據分別減少5、12個,具有更高的預測精確度,這是因為本文所提模型結合了CNN和LSTM的優點,可以更全面地挖掘頻率數據之間的時序特征,從而能夠更精確地表達功率缺額與頻率數據間的非線性關系.

4 結論

在利用測量點發電機的頻率變化估算得到系統COI頻率變化曲線的基礎上,提出一種基于DCNN-LSTM新型電力系統功率缺額評估的新方法,試驗結果表明:

(1) 所提出的COI頻率變化曲線估算方法實現的精度與COI頻率同步測量方法相當,且無需通信,為功率缺額的在線評估提供了技術支持.

(2) 基于DCNN-LSTM的系統功率缺額評估方法由局部頻率測量數據驅動,不依賴系統功率缺額和頻率變化之間的物理模型,能充分挖掘系統功率缺額與頻率數據時序特征之間的相關性.因此將該方法運用于系統功率缺額在線評估時,不僅速度快,而且測試結果精確度高.