追本溯源，攻破易混點

文／韓志琴

函數是初中數學的核心知識，是中考必考內容。一次函數、反比例函數、二次函數是這部分內容的“主角”。從概念到圖像，從性質到應用，從它們之間的關系到它們與其他知識之間的關系，內容錯綜復雜，方法靈活繁多。現將常見的易混點舉例并分析。

一、函數的概念

例1函數y=（m2-m）x2+mx+m+1，若該函數為一次函數，求m的值；若該函數為二次函數，求m的值。

【解析】若該函數為一次函數，得解得m=1。

若該函數為二次函數，則只要考慮二次項前面的系數m2-m≠0 即可，于是解得m≠0且m≠1。

【點評】同學們在解答有關函數表達式問題時，要厘清函數概念，不能模糊不清，否則會導致錯誤。

二、函數的增減性

例2已知點（-3，y1）、（-1，y2）、（1，y3）在下列某一個函數圖像上，且y3＜y1＜y2，那么這個函數是（ ）。

【解析】根據函數增減性，由函數圖像上三個點的橫、縱坐標的大小關系，推測函數類型。選項A 是一次函數，當k＞0 時，函數值y隨x的增大而增大，應有y1＜y2＜y3，故排除。選項B 是二次函數，對稱軸是y軸，所以當x=1或x=-1 時，y2=y3，故排除。選項C 和D 都是反比例函數，根據反比例函數的性質：當k＞0 時，在每一象限內，y隨x的增大而減小；當k＜0 時，在每一象限內，y隨x的增大而增大，k=3＞0，故y2＜y1，故選項C 排除。所以正確選項是D。

【點評】對于選項C 和D，我們還可以借助函數圖像，如圖1、圖2，既能提高正確率，又能感受到數形結合的魅力，提高直觀想象的能力。當然作為選擇題，我們也可以用賦值法代入計算得出正確答案。

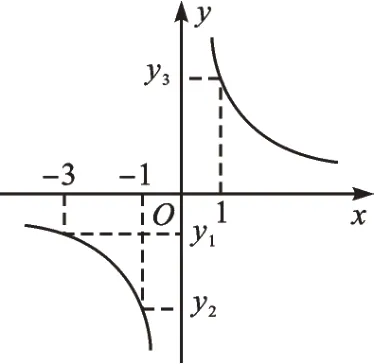
圖1

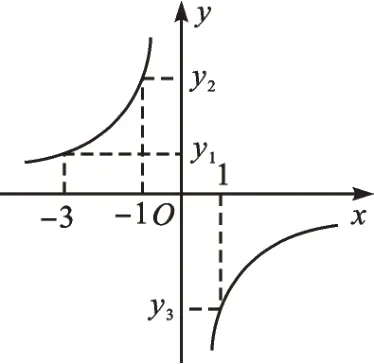
圖2

三、函數的最值

（2）已知一次函數y=kx+b（k≠0），當3≤x≤5 時，對應的函數值為-4≤y≤-2，則函數表達式為________。

【解析】本題需要考慮函數的增減性對點坐標產生的影響，然后用待定系數法求函數表達式。對于一次函數，當k＜0 時，函數y隨自變量x的增大而減小，當k＞0 時，y隨x的增大而增大，所以本題存在兩種可能：①當x=3 時，y=-2，當x=5 時，y=-4，即圖像過點（3，-2）、（5，-4），則一次函數表達式是y=-x+1；②當x=3 時，y=-4，當x=5 時，y=-2，即圖像過點（3，-4）、（5，-2），則一次函數表達式是y=x-7。我們還可以借助圖像很清晰地得出兩種情況（如圖3、圖4）。

圖3

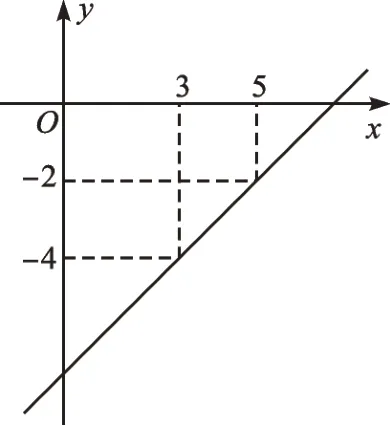
圖4

（3）已知二次函數y=-（x-h）2（h為常數），當自變量x的值滿足2≤x≤5時，與其對應的函數值y的最大值為-1，則h的值為_____。

【解析】由二次函數y=-（x-h）2（h為常數）可知頂點坐標為（h，0），圖像開口向下，當x=h時，函數值ymax=0，不符合題意。由此可見，h不在2≤x≤5的范圍內，所以要分類討論。當h＜2 時，由圖5 可知，當x=2 時，函數值y取最大值，有-（2-h）2=-1，解得h1=1，h2=3（舍去）；當h＞5 時，函數值y取最大值，有-（5-h）2=-1，解得h3=6，h4=4（舍去）。綜上可知，h的值為1或6。

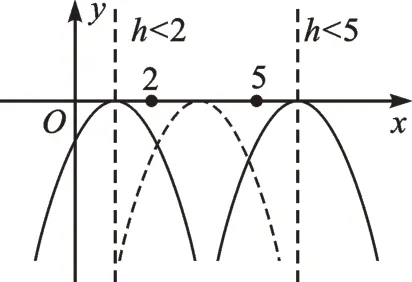
圖5