基于數學抽象素養的高中數學教學研究

武玨 陳艷紅

摘要：《普通高中課程標準》中清晰地指出了六大數學與核心素養，六大數學核心素養之首是數學抽象素養。而向量有著幾何和代數的相結合的身份，向量的理論和方法是解決其他學科：例如向量為物理學研究的重要工具。基于以上背景，本文選擇在抽象素養培養方面具有代表性的平面向量的概念作為研究載體，系統研究數學抽象素養在課堂中的落實問題。

關鍵詞：數學 抽象素養 平面向量概念

一、平面向量知識地位與作用

向量的地位在整個數學體系中非常重要。幾何學為高中數學課程的幾大主線之一，向量的引入為解決傳統綜合幾何問題提供了新的思路，給學生的解題帶來了便利。2017 年頒布的《普通高中中數學課程標準》提出了數學學科核心素養的概念，必修課程包括五個主題，平面向量及其應用在幾何與代數中。

二、新舊課標對高中平面向量的概念要求

新課標提出要理解平面向量的基本要素。大小和方向是平面向量的基本要素，務必要與有向線段的三要素大小、起點和方向進行辨別。此次新《課標》中明確提出這一點，想必是為了讓學生認清平面向量與有向線段的區別與聯系，并進一步給出自由向量的概念。

三、高中數學“平面向量實際背景及基本概念”教材分析

（一）平面向量的概念來自于物理學“力”及生活中“位移”的抽象

史寧中在《數學思想概論》指出抽象深度大概可以分為簡約階段、符號階段和普適階段這三個階段。張勝利，孔凡哲在史寧中教授提出的抽象深度的三個階段的基礎上進一步將數學抽象劃分為四個層次：實物層面、半符號層面、符號層面、形式化層面抽象。比較這些步驟的異同點，認為實物層面抽象和半符號層面抽象屬于史寧中教授提出的簡約階段。根據教材中所出示的抽象過程，可以得出向量的概念是基于物理學中的“力”抽象而成的。

牛頓最開始用的有向線段代表向量，是為了更好地表達力、速度、位移等物理學中基本的要素。在本質上，力的概念包括三個基本要素：力的作用點、力的方向和力的大小。能夠同時表達這三個要素的數學符號就是向量：力的起點用作用點表示，力的方向用箭頭表示，力的大小用長度表示。但在抽象的過程中，史寧中在《高中數學教學的核心問題——數形結合與數學模型》中提出在數學中向量是自由的；物理學或實際應用中，矢量是限定的，矢量的起點尤其重要，因為它是力的作用點。由此得知，這是屬于抽象方式中的“弱抽象”，減弱物理中“力”的特殊性，舍去對象的“作用點”這一特征而僅抽取大小和方向來加以概括，形成比原對象“力”更為普遍、更為一般的“向量”對象的一種抽象方法。

四、教學目標

（一）知識與技能

1.了解向量的物理背景。

2.采用類比的方式，將物理中用有向線段表示力的大小和方向來掌握向量的表示方式，了解物理中矢量與向量間的區別。

3.掌握零向量、單位向量這兩個特殊的向量的概念，學會辨別共線向量、相等向量以及相反向量。

（二）過程與方法

通過生活中的位移舉例子，在熟悉的現實世界中抽象出向量的概念，掌握向量的表示方法。

（三）情感態度與價值觀

1.通過觀察生活實例，在抽象出平面向量的概念過程中來提升學生的數學抽象素養。

2.培養學生對數學學科的探究精神。

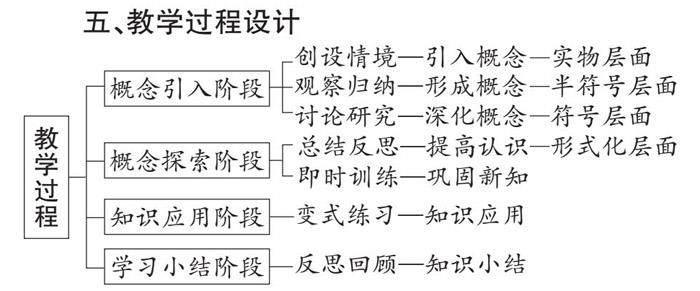
五、教學過程設計

（一）創設情境——引入概念

實物層面抽象：通過“位移”和“力”抽象出向量的概念

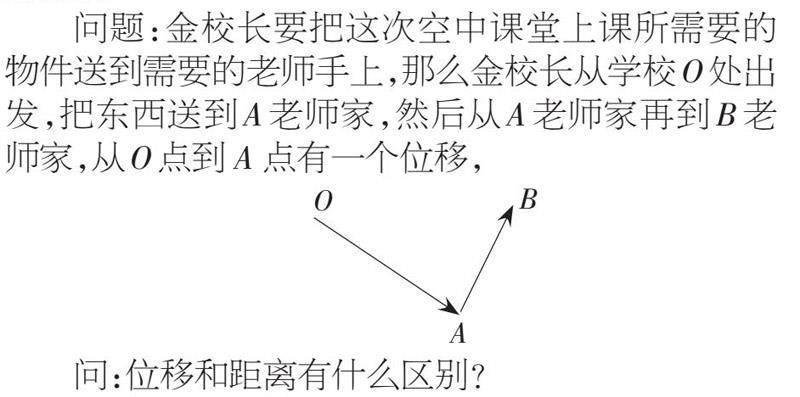
問題：金校長要把這次空中課堂上課所需要的物件送到需要的老師手上，那么金校長從學校O處出發，把東西送到A老師家，然后從A老師家再到B老師家，從O點到 A 點有一個位移，

[A][O][B] 問：位移和距離有什么區別？

學生預設：位移具有方向，而距離沒有方向。

（設計意圖：讓學生在生活中去發現位移和距離之間的區別和聯系，引導學生用數學的眼光看世界。

（二）觀察歸納——形成概念

半符號層面抽象：類比數字的由來提出提煉共性、總結概念

問題：現實世界中同學們還發現是否有既有大小又有方向的量嗎？請同學們舉例說明，并相互討論這些量是如何體現大小的方向？

學生預設：學生能容易地舉出重力、浮力、作用力等物理中學過的量。

（設計意圖：掌握抽象概念中豐富的實例，幫助學生提煉共性，初步認識概念的，為下一步的更進一步抽象概括做預備。）

教師：在物理學科中，這些既有大小又有方向的量統稱矢量；在數學中如長度、時間等這些只有大小有方向的量統稱標量。由同學們的思考和舉例可知，現實世界中有只有大小沒有方向的量，也有既有大小又有方向的量。類似于從一棵樹、一朵花中抽象出“1”這個大小的數，數學中對位移、力既有大小又有方向的量進行抽象形成一種新的量——向量。

（三）討論研究——深化概念

符號層面抽象：得到向量概念數學符號語言表達（幾何表達）

老師：那么向量可以如何表示呢？請按照要求畫出物體所受到的“力”學生活動：借助物理情境，借助物理背景進行研究。學生很容易找到各力的大小和方向。

老師：現在，只研究其具體的大小和方向，能觀察出什么呢？

學生預設：具體物體可抽象出成點的概念，力可抽象成有向線段的概念。

老師：初中時學過線段可以用AB、a 表示，有向線段應該怎樣表示呢？數學上規定了一種比較形象的表示方法，記做：AB，或者用[a→]表示，注意AB和BA不是同一個向量。

（設計意圖：學生已經知道線段的表示方法，有向線段在線段的基礎上加上一個箭頭即可，類比實數大小的表示，得到向量大小的表示方式。）

老師：由相等向量的概念可以得出，它的方向和模確定一個向量。由此，同學們可以用有向線段來表示數學中的向量，那么向量就等同于有向線段嗎？向量和物理學中的“力”有什么區別？

總結：向量沒有起點，而有向線段有起點，力也有作用點，但是向量只有“大小和方向”兩個要素，力這是舍棄了“力”中的作用點抽象而成的。

（四）總結反思——提高認識

形式化層面抽象：向量概念的系統化和普適化。

1.向量的模

問題：向量能比較大小嗎？

老師：向量有大小這樣的屬性，大小是可以比較的，但是方向卻無法比較大小。實數的大小用絕對值表示，于此進行類比，[AB]記作AB的模。

2.零向量和單位向量的認識

問題：同學們，在我們學習的數中，哪些實數比較特殊？

老師：數字0、1 比較特殊。你能說出這兩個數字特殊的理由嗎？

學生預設：在實數中，0正數和負數的分界點；1 時常作為“單位”，起到了至關重要的作用。

（設計意圖：通過類比實數的方法得處向量有關的概念，提升學生的類比思維。）

老師：同學們思考類比特殊實數是否能得出特殊向量呢？

學生預設：認為零向量的長度是 0，單位向量的長度是 1，最為特殊，引出單位向量和零向量。

（設計意圖：這表明他們已經在把向量集與實數集作類比。以梳理邏輯出發，從內在聯系進行原理型抽象，自然會想到零向量、單位向量的特殊性。）

（設計意圖：通過問題驅動的方式設計教學活動，突出了學生在課堂上的主體地位。學生經歷完整的數學抽象，再從具體到抽象再到概括的過程。）

六、總結鞏固——知識小結

教師引導學生自主總結本節課所學習的向量的概念、幾個特殊的向量、向量之間的關系等相關知識。教師總結概念抽象的過程：觀察實例、提煉共性、總結概念、得到概念數學符號語言表達、建立完整的體系。