基于低增益LESO的有機(jī)廢液焚燒系統(tǒng)控制算法研究

李艷 王鑫 胡振 戴慶瑜

摘?要：有機(jī)廢液焚燒過(guò)程存在強(qiáng)耦合、強(qiáng)干擾、非線性、不確定性等問(wèn)題導(dǎo)致以數(shù)學(xué)模型為基礎(chǔ)的控制策略較難取得良好的控制效果.LADRC可利用LESO對(duì)以上因素進(jìn)行估計(jì)并補(bǔ)償，但當(dāng)觀測(cè)帶寬受限時(shí)會(huì)導(dǎo)致LESO觀測(cè)能力不足，從而使得控制效果不佳.針對(duì)以上問(wèn)題，本文對(duì)LADRC進(jìn)行改進(jìn)，首先將實(shí)際系統(tǒng)轉(zhuǎn)化為積分串聯(lián)形式的理想系統(tǒng)，然后分別將控制信號(hào)作用于理想系統(tǒng)和實(shí)際系統(tǒng)并得出二者的輸出偏差，再采用PI控制器對(duì)其進(jìn)行補(bǔ)償，彌補(bǔ)了因低增益LESO觀測(cè)能力不足導(dǎo)致控制效果欠佳的缺陷.將改進(jìn)后的LADRC應(yīng)用于有機(jī)廢液焚燒系統(tǒng)，仿真結(jié)果表明改進(jìn)后的LADRC采用低增益LESO不僅能有效解決以上所描述的有機(jī)廢液焚燒過(guò)程中存在的各控制難點(diǎn)，并且相較傳統(tǒng)的LADRC具有更好的階躍跟蹤能力、抗干擾性和魯棒性.

關(guān)鍵詞：廢液焚燒；LADRC控制；低增益LESO；PI補(bǔ)償；蒙特卡洛實(shí)驗(yàn)

中圖分類號(hào)：TP273

文獻(xiàn)標(biāo)志碼： A

文章編號(hào)：2096-398X（2023）04-0143-08

Abstract：The organic waste liquid incineration process has problems such as strong coupling，strong interference，non-linearity，uncertainty，etc.，which makes it difficult to achieve good control effects for control strategies based on mathematical models.LADRC can use LESO to estimate and compensate for the above factors，but when the observation bandwidth is limited，it will lead to insufficient LESO observation ability，which makes the control effect poor.This article improves LADRC.First，the actual system is transformed into an ideal system in integral series，and then the control signal is applied to the ideal system and the actual system to obtain the output deviation of the two，and then the PI controller is used to compensate it，it makes up for the defect of poor control effect due to insufficient observation ability of low-gain LESO.Applying the improved LADRC to the organic waste incineration system，the simulation results show that the improved LADRC using low-gain LESO can not only effectively solve the control difficulties in the organic waste incineration process described above，but also has better step tracking ability，anti-jamming and robustness than the traditional LADRC.

Key words：waste liquid incineration；LADRC control；low gain LESO；PI compensation；monte carlo experiment

0?引言

隨著醫(yī)藥、化工等行業(yè)的用水量和排放量的不斷增加，有機(jī)廢液對(duì)環(huán)境造成的污染日益嚴(yán)重，因此需要將有機(jī)廢液無(wú)害化處理后排放.對(duì)于濃度高、成分復(fù)雜、沒(méi)有回收價(jià)值的有機(jī)廢液通常采用焚燒的方法進(jìn)行處理［1］.影響廢液焚燒效果及焚燒過(guò)程安全的關(guān)鍵參數(shù)有爐膛溫度、煙氣含氧量及爐膛負(fù)壓，而這三個(gè)變量之間存在嚴(yán)重的耦合.另外，廢液成分會(huì)隨時(shí)間變化，導(dǎo)致廢液熱值變化較大，因此廢液焚燒過(guò)程具有干擾頻繁、時(shí)變、非線性、不確定性等特征，從而使得以數(shù)學(xué)模型為基礎(chǔ)的控制方法和傳統(tǒng)PID控制均難以取得良好的控制效果.

LADRC能夠?qū)⒛Ｐ椭形唇５牟糠帧⑼獠繑_動(dòng)和耦合視為“總擾動(dòng)”，通過(guò)觀測(cè)器實(shí)時(shí)對(duì)其進(jìn)行觀測(cè)并補(bǔ)償［2，3］，可有效解決有機(jī)廢液焚燒過(guò)程中存在的以上問(wèn)題.但線性擴(kuò)張狀態(tài)觀測(cè)器的觀測(cè)能力會(huì)受到帶寬的限制，當(dāng)觀測(cè)器的帶寬選擇較小時(shí)會(huì)出現(xiàn)觀測(cè)準(zhǔn)確性下降的問(wèn)題［4］.高志強(qiáng)等在文獻(xiàn)［5，6］中指出通過(guò)提高擴(kuò)張狀態(tài)觀測(cè)器的帶寬來(lái)解決此類問(wèn)題.但在實(shí)際應(yīng)用中，高帶寬意味著高成本，并且高帶寬會(huì)使得系統(tǒng)的穩(wěn)定性下降，對(duì)外界干擾更為敏感，因此上述問(wèn)題不能僅僅依靠提高帶寬來(lái)解決.

對(duì)于帶寬受限的問(wèn)題，文獻(xiàn)［7］提出改變誤差估計(jì)值的增益，相當(dāng)于閉環(huán)系統(tǒng)增加了一個(gè)一階微分環(huán)節(jié)，減小擾動(dòng)觀測(cè)的相位滯后程度，提高狀態(tài)觀測(cè)器的實(shí)時(shí)觀測(cè)能力，通過(guò)仿真驗(yàn)證其控制效果良好；文獻(xiàn)［8］ 提出采用并聯(lián)型 LESO 結(jié)構(gòu)進(jìn)行控制，以期望獲得更優(yōu)秀的擾動(dòng)觀測(cè)性能，經(jīng)過(guò)仿真驗(yàn)證效果控制效果良好；文獻(xiàn)［9］采用慣性環(huán)節(jié)對(duì)對(duì)象的延遲特性進(jìn)行補(bǔ)償，并針對(duì)自抗擾控制參數(shù)難調(diào)整的問(wèn)題采用模糊規(guī)則進(jìn)行調(diào)整，仿真驗(yàn)證具有較好的魯棒性.

本文針對(duì)LESO帶寬受限的問(wèn)題，為方便工程實(shí)現(xiàn)，對(duì)LADRC進(jìn)行改進(jìn)［10］：采用低增益LESO對(duì)擾動(dòng)進(jìn)行觀測(cè)，將忽略掉干擾的實(shí)際模型視為理想模型，使用參數(shù)相同的線性自抗擾控制器分別對(duì)理想模型和實(shí)際模型進(jìn)行控制，并采用PI控制器對(duì)兩者輸出的偏差進(jìn)行補(bǔ)償.將改進(jìn)后的LADRC應(yīng)用于有機(jī)廢液焚燒系統(tǒng)的控制中，通過(guò)MATLAB仿真驗(yàn)證其有效性.

1?焚燒過(guò)程數(shù)學(xué)模型

本研究團(tuán)隊(duì)面向有機(jī)廢液焚燒過(guò)程采用機(jī)理法進(jìn)行建模，通過(guò)實(shí)際數(shù)據(jù)的驗(yàn)證結(jié)果來(lái)看，所建立的數(shù)學(xué)模型能夠滿足控制系統(tǒng)設(shè)計(jì)的需要［11］.

焚燒過(guò)程傳遞函數(shù)矩陣的具體表達(dá)式為：

式（1）中：Tg表示爐膛溫度，WO2表示煙氣氧含量，Pg表示爐膛負(fù)壓，Wc表示天然氣流量，Wa表示送風(fēng)量，Wg表示引風(fēng)量，Wf表示廢液流量.

式（1）中傳遞函數(shù)矩陣為非對(duì)角線矩陣，說(shuō)明三條控制回路之間存在強(qiáng)耦合；其次，廢液流量和成分的變化會(huì)對(duì)三者產(chǎn)生較大的影響，因此，焚燒過(guò)程存在強(qiáng)時(shí)變干擾；另外，廢液焚燒過(guò)程包含一系列的物理、化學(xué)變化，整個(gè)過(guò)程存在強(qiáng)非線性和時(shí)變性，而且以上數(shù)學(xué)模型是忽略掉一些非線性因素而得到的，存在未建模的部分.

2?線性自抗擾控制器設(shè)計(jì)及誤差分析

2.1?線性自抗擾控制器的設(shè)計(jì)

線性自抗擾控制技術(shù)將多輸入多輸出系統(tǒng)控制回路之間的耦合視為擾動(dòng)，經(jīng)過(guò)補(bǔ)償后等效為多個(gè)單輸入單輸出的系統(tǒng)進(jìn)行控制［12］.

本文以壓力-引風(fēng)量通道為例進(jìn)行研究，根據(jù)傳遞函數(shù)可知此通道為二階系統(tǒng)，可以用微分方程表示為：

式（5）中：z1，z2，z3分別表示輸出的估計(jì)值，輸出微分的估計(jì)值和“總擾動(dòng)”的估計(jì)值.β01，β02，β03為L(zhǎng)ESO的增益值，可以通過(guò)調(diào)節(jié)參數(shù)改變觀測(cè)器的觀測(cè)能力.圖1給出線性自抗擾控制器的結(jié)構(gòu)圖，圖2給出壓力-引風(fēng)量通道的模擬結(jié)構(gòu)圖.

由式（15）可知：只有觀測(cè)器帶寬ωo→∞時(shí)，觀測(cè)誤差才會(huì)趨于零.這與工程實(shí)際應(yīng)用中ωo不能夠無(wú)限制增大相悖.

采用MATLAB對(duì)爐膛壓力-引風(fēng)量通道施加y=sint的干擾信號(hào)，分析觀測(cè)器的觀測(cè)能力，不同ωo的擾動(dòng)觀測(cè)信號(hào)如圖3所示.當(dāng)觀測(cè)器的帶寬ωo較小時(shí)，觀測(cè)器會(huì)出現(xiàn)幅值衰減和相位滯后的問(wèn)題，觀測(cè)器很難跟蹤到實(shí)際的擾動(dòng)，而當(dāng)觀測(cè)器的帶寬ωo取得較大值時(shí)，觀測(cè)器可以取得較好的跟蹤效果，甚至帶寬取值足夠大時(shí)，觀測(cè)所得信號(hào)與實(shí)際擾動(dòng)信號(hào)重合，但在初始時(shí)刻，觀測(cè)誤差會(huì)隨著ωo的增大而增大，如圖3所示.

因此，通過(guò)仿真實(shí)驗(yàn)也說(shuō)明增益較小的擴(kuò)張狀態(tài)觀測(cè)器所觀測(cè)擾動(dòng)的誤差較大.

3?改進(jìn)線性自抗擾控制器設(shè)計(jì)及分析

3.1?改進(jìn)線性自抗擾控制器的設(shè)計(jì)

針對(duì)前文提出的傳統(tǒng)LADRC的觀測(cè)器在帶寬較小時(shí)觀測(cè)誤差較大的問(wèn)題，結(jié)合PI控制的原理，對(duì)傳統(tǒng)LADRC控制器進(jìn)行了改進(jìn)，改進(jìn)后的結(jié)構(gòu)框圖如圖4所示.其中虛線框內(nèi)為傳統(tǒng)LADRC的基本結(jié)構(gòu)，包含線性誤差反饋控制律（LSEF）和線性擴(kuò)張狀態(tài)觀測(cè)器（LESO）.

傳統(tǒng)LADRC控制量u由偏差信號(hào)及其微分和擾動(dòng)估計(jì)值線性組合而成，當(dāng)LESO的帶寬取值較小時(shí)，觀測(cè)器難以準(zhǔn)確估計(jì)擾動(dòng)信號(hào)，系統(tǒng)難以達(dá)到所需要的控制效果.改進(jìn)后的LADRC采用低增益LESO對(duì)擾動(dòng)進(jìn)行估計(jì)，其估計(jì)值和實(shí)際值會(huì)有偏差，即實(shí)際模型不能被等效為理想模型.當(dāng)控制量均為u0時(shí)，實(shí)際模型的輸出和理想模型的輸出也存在偏差.本文將實(shí)際模型與理想模型的輸出偏差通過(guò)PI控制器補(bǔ)償?shù)娇刂屏縰中，改善了控制效果.

3.2?改進(jìn)線性自抗擾控制器的穩(wěn)定性分析

根據(jù)線性自抗擾控制技術(shù)的思想，外部干擾信號(hào)、回路之間的耦合及建模過(guò)程中忽略的部分都被定義為總擾動(dòng)，通過(guò)LESO和PI控制器進(jìn)行補(bǔ)償，那么原本多變量系統(tǒng)的第三條回路可以被等效為圖5所示的單回路系統(tǒng)，因此只需對(duì)此單回路系統(tǒng)的穩(wěn)定性進(jìn)行證明.

由圖6整理可得：

上述的結(jié)構(gòu)變換簡(jiǎn)化了改進(jìn)型LADRC的穩(wěn)定性證明.根據(jù)勞斯判據(jù)可以得出系統(tǒng)穩(wěn)定時(shí)參數(shù)的取值范圍［17，18］，從理論上來(lái)講，勞斯表中第一列系數(shù)均為正即可保證系統(tǒng)穩(wěn)定的同時(shí)求得參數(shù)范圍，而在實(shí)際中，一般情況會(huì)首先選取參數(shù)ωc和ωo，將其代入閉環(huán)特征方程，求得特征多項(xiàng)式，再依據(jù)勞斯表判斷系統(tǒng)的穩(wěn)定性.

4?仿真分析

式（8）和（11）提出的線性自抗擾控制器參數(shù)整定方法是針對(duì)二階對(duì)象設(shè)計(jì)的，而文獻(xiàn)［19］提出典型的工業(yè)控制對(duì)象都可以采用二階線性自抗擾控制器進(jìn)行控制，因此本文數(shù)學(xué)模型的前兩條通道也采用二階線性自抗擾控制器進(jìn)行控制.

為驗(yàn)證改進(jìn)后LADRC的控制性能，選取PID控制和傳統(tǒng)的LADRC控制作為對(duì)照，其中LADRC控制與PI-LADRC控制的參數(shù)一致，根據(jù)帶寬法進(jìn)行整定，首先選擇ωo=5ωc，此時(shí)需要調(diào)節(jié)的參數(shù)僅為ωc.逐步增大ωc，直到噪聲影響難以承受導(dǎo)致系統(tǒng)輸出波動(dòng)時(shí)，停止調(diào)節(jié)ωc；逐步減小ωo至系統(tǒng)輸出恢復(fù)穩(wěn)定，再次調(diào)節(jié)ωc，依次循環(huán)調(diào)節(jié)，直到滿足控制要求.PI-LADRC控制的PI補(bǔ)償器參數(shù)按照經(jīng)驗(yàn)法進(jìn)行整定；PID控制的參數(shù)整定根據(jù)臨界震蕩法（Z-N法）進(jìn)行整定，具體參數(shù)見表1所示.

4.1?階躍響應(yīng)及解耦效果驗(yàn)證

為驗(yàn)證三種控制方式的階躍響應(yīng)效果和解耦能力.在t=0 s、150 s和300 s時(shí)分別對(duì)溫度、氧含量以及壓力回路單獨(dú)施加幅值為1、2、3的單位階躍信號(hào).各回路的輸出響應(yīng)曲線如圖7所示.

觀察分析圖7的輸出曲線，三種控制方案的輸出都能夠穩(wěn)定在設(shè)定值，所以三種控制方案均具有良好的跟蹤能力，但采用PID控制存在較大的超調(diào)量和調(diào)節(jié)時(shí)間，而LADRC控制和PI-LADRC控制沒(méi)有超調(diào)量，調(diào)節(jié)時(shí)間較小.當(dāng)分別向三條通道施加設(shè)定值時(shí)，PID控制的解耦能力差，難以取得令人滿意的解耦效果.LADRC控制的解耦能力優(yōu)于PID控制，但與PI-LADRC控制存在一定的差距.

為了使PI-LADRC控制的效果更有說(shuō)服力，分別對(duì)三種控制策略下的超調(diào)量（σ%）和調(diào)節(jié)時(shí)間（ts）進(jìn)行計(jì)算，計(jì)算結(jié)果如表2所示.

4.2?抗擾效果對(duì)比驗(yàn)證

在廢液焚燒的過(guò)程中控制系統(tǒng)可能出現(xiàn)執(zhí)行器誤動(dòng)作的現(xiàn)象，且廢液燃燒時(shí)的熱值實(shí)時(shí)變化，因而有必要衡量控制器的抗擾能力.

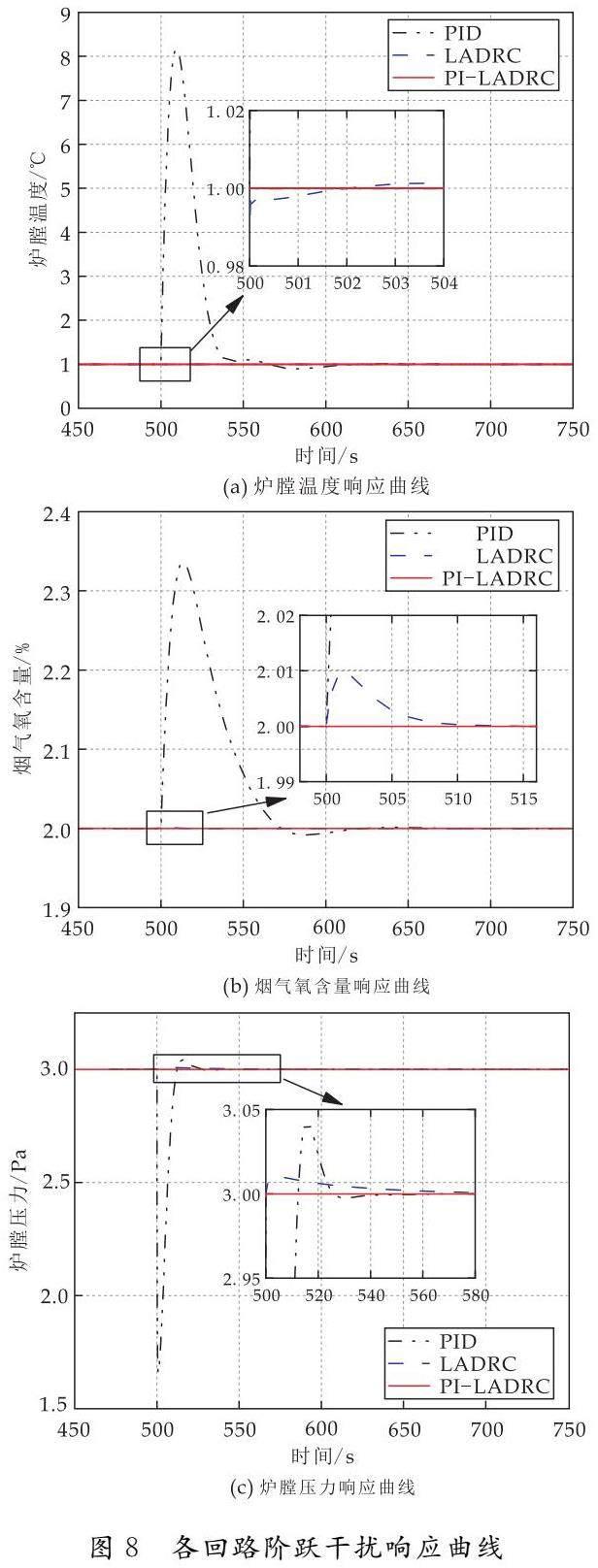
若執(zhí)行器出現(xiàn)誤動(dòng)作的現(xiàn)象，可以將其等效為回路出現(xiàn)一個(gè)階躍擾動(dòng)信號(hào)，因此需要在上述實(shí)驗(yàn)的基礎(chǔ)上研究控制器抗階躍干擾的能力，當(dāng)t=500 s時(shí)，分別向三條通道施加幅值為1的階躍信號(hào)作為干擾，各回路的階躍干擾響應(yīng)曲線如圖8所示.

由圖8的響應(yīng)曲線可知，以階躍信號(hào)作為干擾，PID控制下各回路響應(yīng)曲線均出現(xiàn)了大幅突變，LADRC控制下各回路響應(yīng)曲線也出現(xiàn)了不同程度的變化，但比PID控制效果優(yōu)秀，而采用PI-LADRC控制時(shí)各回路響應(yīng)曲線未出現(xiàn)明顯變化，這說(shuō)明PI-LADRC控制對(duì)于階躍信號(hào)干擾具有更好的抗擾能力.

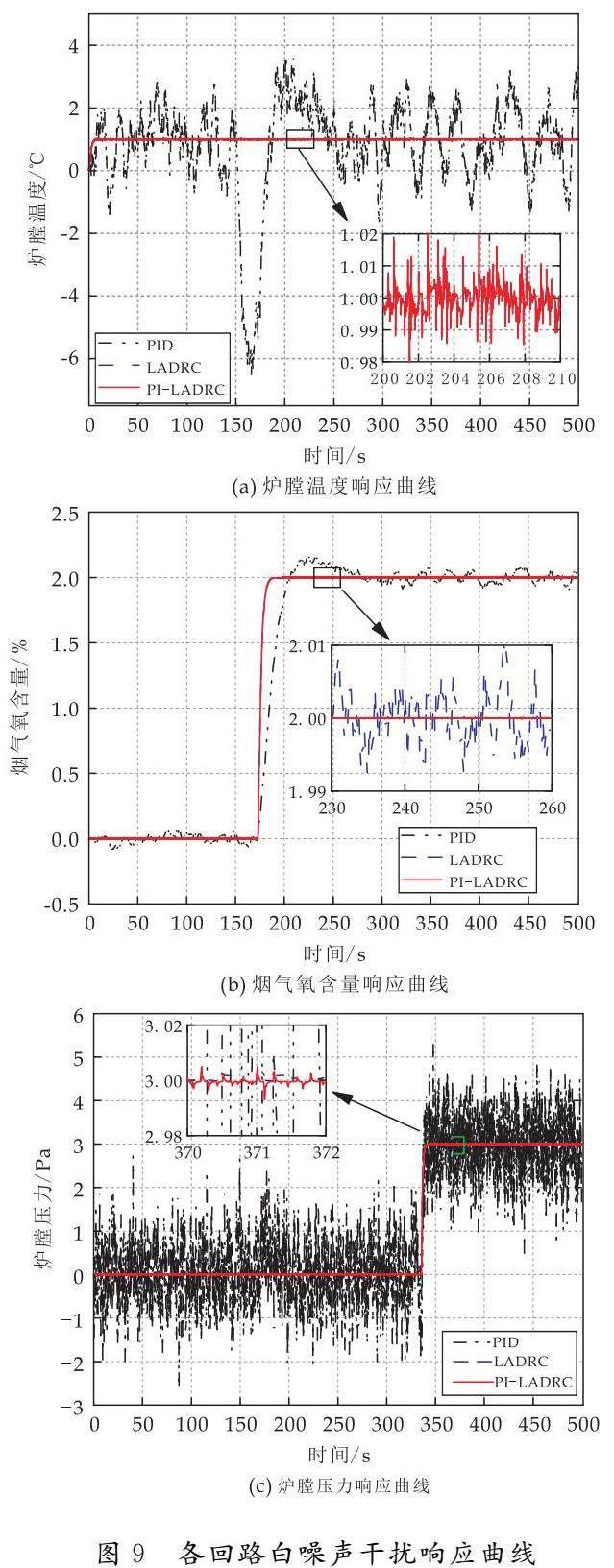
熱值的變化會(huì)對(duì)系統(tǒng)的抗擾能力產(chǎn)生影響，而熱值變化可以視為白噪聲信號(hào)，因此在t=0時(shí)刻加入擾動(dòng)信號(hào).各回路加入白噪聲干擾信號(hào)后的響應(yīng)曲線如圖9所示.

根據(jù)圖9的響應(yīng)曲線，加入白噪聲干擾信號(hào)后，PID控制受到白噪聲的干擾，導(dǎo)致控制回路的輸出出現(xiàn)了不同程度的失真，LADRC控制受白噪聲的影響較小，而PI-LADRC控制相較于LADRC控制所受的影響更小，并且能夠更加快速的恢復(fù)穩(wěn)定狀態(tài).

4.3?魯棒性對(duì)比分析

本文采用蒙特卡洛實(shí)驗(yàn)驗(yàn)證控制器的魯棒性，以4.1節(jié)的實(shí)驗(yàn)為基礎(chǔ)，在保持仿真條件和控制參數(shù)不變的情況下，分別對(duì)主通道傳遞函數(shù)分母的最高次項(xiàng)增加或減少10%的參數(shù)攝動(dòng)以及向主通道增加慣性環(huán)節(jié)（1/0.01s+1）來(lái)模擬模型失配情況.實(shí)驗(yàn)結(jié)果的參數(shù)攝動(dòng)具體變化為：[SX（]-（46.484s+28.63）[]（6.3±0.63·i）s2+36.97s+5.72[SX）]，其中i=0，1，2，…，7，8.不同控制策略在模型失配情況下的控制曲線如圖10～12所示.性能指標(biāo)統(tǒng)計(jì)表3給出在蒙特卡洛實(shí)驗(yàn)下三種控制方案對(duì)于三條通道調(diào)節(jié)時(shí)間和超調(diào)量變化的范圍.

根據(jù)圖10～12和表3，采用三種控制方案對(duì)爐膛溫度、煙氣氧含量和爐膛壓力進(jìn)行控制，發(fā)生相同的參數(shù)攝動(dòng)時(shí)，PID控制的超調(diào)量和調(diào)節(jié)時(shí)間遠(yuǎn)大于LADRC控制和PI-LADRC控制，LADRC控制的調(diào)節(jié)時(shí)間大于PI-LADRC控制.

PID控制的點(diǎn)集分布在整個(gè)區(qū)域內(nèi)，LADRC控制和PI-LADRC控制的點(diǎn)集分布在較小的區(qū)域，且PI-LADRC控制分布的范圍更小.這說(shuō)明與?PID控制方案和LADRC控制方案相比，PI-LADRC控制在設(shè)定值跟蹤方面的魯棒性更強(qiáng).

5?結(jié)論

針對(duì)LADRC控制帶寬受限問(wèn)題，本文通過(guò)理論推導(dǎo)和仿真分析驗(yàn)證了LESO的帶寬和觀測(cè)誤差之間存在矛盾，提出了以低增益LESO為基礎(chǔ)的PI-LADRC控制技術(shù)，通過(guò)仿真驗(yàn)證，PI-LADRC控制在觀測(cè)器帶寬取值較小的情況下能夠解決焚燒過(guò)程存在的強(qiáng)耦合、時(shí)滯、強(qiáng)干擾等問(wèn)題，相比于傳統(tǒng)PID控制和LADRC控制具有更強(qiáng)的解耦能力、抗干擾能力和魯棒性能.

參考文獻(xiàn)

［1］ 鐘?璟，韓光魯，陳?群.高鹽有機(jī)廢水處理技術(shù)研究新進(jìn)展［J］.化工進(jìn)展，2012，31（4）：920-926.

［2］ 韓京清.從PID技術(shù)到“自抗擾控制”技術(shù)［J］.控制工程，2002，9（3）：13-18.

［3］ 韓京清.自抗擾控制技術(shù)［J］.前沿科學(xué)，2007（1）：24-31.

［4］ 李?杰，齊曉慧，夏元清.線性/非線性自抗擾切換控制方法研究［J］.自動(dòng)化學(xué)報(bào)，2016，42（2）：202-212.

［5］ 高志強(qiáng).自抗擾控制思想探究［J］.控制理論與應(yīng)用，2013，30（12）：1 498-1 510.

［6］ Gao Zhiqiang.Scaling and bandwidth-parameterization based controller tuning［C］//Proceedings of the 2003 American Control Conference.Colorado，USA：IEEE，2003：4 989-4 996.

［7］ 顧?健，艾?勇，單?欣.線性擴(kuò)張狀態(tài)觀測(cè)器的改進(jìn)及在空間光通信粗跟蹤的應(yīng)用［J］.紅外與激光工程，2016，45（3）：263-270.

［8］ 郭海宇，楊俊友，張曉光.永磁同步電梯門機(jī)改進(jìn)型自抗擾控制策略［J］.哈爾濱工業(yè)大學(xué)學(xué)報(bào)，2018，50（9）：191-198.

［9］ 杜?鳴，牛玉廣，潘翔峰，等.基于改進(jìn)型模糊線性自抗擾控制器的SCR脫硝系統(tǒng)優(yōu)化控制［J］.動(dòng)力工程學(xué)報(bào)，2021，41（9）：743-748，757.

［10］ Jin H，Liu L，Lan W，et al.On stability and robustness of linear active disturbance rejection control：A small gain the orem approach［C］// Proceedings of the 36th Chinese Control Conference.Dalian，China：IEEE，2017：3 242-3 247.

［11］ 李?艷，胡?振，魚?晨，等.面向控制的廢液焚燒過(guò)程的建模與分析＼[J/OL＼].控制工程：1-9＼[2023-07-02＼].https：//doi.org/10.14107/j.cnki.kzgc.20200916.

［12］ 李鵬威，王?京.平整軋制多變量系統(tǒng)的線性自抗擾解耦控制［J］.武漢科技大學(xué)學(xué)報(bào)，2019，42（5）：339-342.

［13］ 吳?丹，趙?彤，陳?懇.快速刀具伺服系統(tǒng)自抗擾控制的研究與實(shí)踐［J］.控制理論與應(yīng)用，2013，30（12）：1 534-1 542.

［14］ 陳增強(qiáng)，鄭月敏，孫明瑋，等.含發(fā)電速率約束的三區(qū)域互聯(lián)電力系統(tǒng)自抗擾控制［J］.哈爾濱工程大學(xué)學(xué)報(bào)，2020，41（9）：1 312-1 319.

［15］ 黃?宇，王佳榮.水輪機(jī)調(diào)速系統(tǒng)的線性自抗擾優(yōu)化控制［J］.系統(tǒng)仿真學(xué)報(bào)，2016，28（12）：3 033-3 040.

［16］ 袁?東，馬曉軍，曾慶含，等.二階系統(tǒng)線性自抗擾控制器頻帶特性與參數(shù)配置研究［J］.控制理論與應(yīng)用，2013，30（12）：1 630-1 640.

［17］ 付?瑩，李冰玉，郭繼寧.基于線性自抗擾控制的高頻真空感應(yīng)爐溫度控制［J］.中國(guó)鑄造裝備與技術(shù)，2020，55（3）：48-53.

［18］ 金輝宇，劉麗麗，蘭維瑤.二階系統(tǒng)線性自抗擾控制的穩(wěn)定性條件［J］.自動(dòng)化學(xué)報(bào)，2018，44（9）：1 725-1 728.

［19］ 黃?宇，張偉婷，金秀章.SCR脫硝系統(tǒng)的線性自抗擾串級(jí)控制研究［J］.中國(guó)電機(jī)工程學(xué)報(bào)，2018，38（18）：5 518-5 526.

【責(zé)任編輯：蔣亞儒】

基金項(xiàng)目：陜西省科技廳重點(diǎn)研發(fā)計(jì)劃項(xiàng)目（2023-YBGY-277）; 陜西省咸陽(yáng)市重點(diǎn)研發(fā)計(jì)劃項(xiàng)目（L2022ZDYFSF047）

作者簡(jiǎn)介：李?艷（1972—），女，四川樂(lè)山人，副教授，研究方向：工業(yè)自動(dòng)化、智能檢測(cè)與智能控制