自旋張量-動量耦合作用下自旋1玻色-愛因斯坦凝聚體的調制不穩定性

李冠強 唐勁羽 彭娉 竹有章 牛海波

摘?要：研究了自旋張量-動量耦合作用下自旋1玻色-愛因斯坦凝聚體（BEC）中連續波態的調制不穩定性.借助于擾動頻率和波數之間的色散關系，研究發現系統的調制不穩定性可以用六個不等價的分支來充分描述.進一步分析表明，在給定拉曼耦合強度和原子-原子相互作用強度下，動量空間中調制不穩定增長率分布關于k=0是對稱的，并可用若干不同的不穩定帶來表征.本文也計算了在相同參數條件下自旋-軌道耦合自旋1 BEC中調制不穩定的增長率，并與前者的結果進行了比較.除了不同的譜帶數目和譜帶強度外，具有自旋-軌道耦合BEC的調制不穩定性實際上只與三個不等價的分支有關，這源于它與具有自旋張量-動量耦合BEC系統的單粒子哈密頓量的不同對稱性.這些結果不僅有助于人們理解系統基態的非線性動力學性質，而且有助于對系統中可能存在的非線性激發進行系統分析.

關鍵詞：玻色-愛因斯坦凝聚；自旋張量-動量耦合；自旋-軌道耦合；調制不穩定性

中圖分類號：O474

文獻標志碼： A

文章編號：2096-398X（2023）04-0195-08

Abstract：The modulation instabilities of continuous-wave states in spin-1 Bose-Einstein condensates under spin tensor-momentum couplings are investigated.With the help of the dispersion relation between perturbation frequency and wavenumber，we find that the modulation instability of the system can be adequately described by six unequal branches.Further analysis shows that，for a given Raman coupling strength and atom-atom interaction strength，the modulation instability growth rate distribution in momentum space is symmetric about k=0?and can be characterized by several different instability bands.We also calculate the growth rate of modulation instability in spin-orbit coupled spin-1 Bose-Einstein condensates under the same parameter conditions and compare with the former results.Besides the different number of bands and band intensities，the modulation instability of Bose-Einstein condensates with spin-orbit coupling is actually only related to three unequal branches，which stem from its different symmetries of the single-particle Hamiltonian of a spin-tensor-momentum coupled BEC system.These results not only contribute to the understanding of the nonlinear dynamic properties of the ground state，but also to the analysis of possible nonlinear excitations in the system.

Key words：Bose-Einstein condensate; spin tensor-momentum coupling; spin-orbit coupling; modulation instability

0?引言

超冷原子氣體的玻色-愛因斯坦凝聚體（BEC）由于其純凈性和可控性成為量子模擬的理想平臺［1，2］.在實驗上，超冷氣體中原子之間的相互作用可以通過費什巴赫共振技術來進行調節［3］.單組分和多組分BEC中物質波的非線性相干結構和動力學特性是展現這種技術的優良范例［4］.由于實現了超低溫費米氣體BCS-BEC渡越的幺正極限，使得探索強關聯效應和超冷分子物理的性質成為了可能［5，6］.用于捕獲超低溫氣體的光學晶格的出現在這種可控性方面又向前邁進了一步［7］.對傳統凝聚態物理及其相關領域中的許多現象和效應，如超流-莫特絕緣轉變［8］和Anderson局域化［9］，人們也已經借助超冷原子平臺進行了大量研究并做出重新理解.

由于超冷原子人工規范場可以在實驗上實現，使得在最近發展的拓撲量子物質和非平衡動力學過程中推廣新的概念和構想變得更加靈活［10，11］.通過原子與兩束激光的相互作用，原子的自旋和軌道運動可以耦合在一起，形成中性玻色原子中的自旋-軌道耦合（SOC）［12，13］.具有SOC作用BEC的研究為發現非零動量的平面波相和條紋相等奇異態提供了新的機會［14］.同時，各種SOC的新變種，包括自旋-軌道角動量耦合［15-17］和自旋張量-動量耦合（STMC）［18，19］，被提出用于研究新的物理機制.磁條紋孤子的研究進展［20］和亮孤子［21］也顯示出STMC項所具有的非平庸特性.

如果關注具有STMC作用BEC的基態穩定性和物質波的動力學，目前還存在一個需要解決的基本問題.這就是連續波態對小擾動的調制不穩定性，它引發了常數振幅連續波向具有調制振幅態的動力學轉換［22］.任何非線性系統的調制不穩定特性不僅決定了系統中非線性激發的種類，而且影響著系統的動力學演化特性，包括基態的壽命.在實驗中，人們證實了調制不穩定性是孤波和孤波陣列形成的必要機制［23-25］.單組分BEC的調制不穩定性只存在于原子-原子間為吸引的相互作用情形中［26，27］.對于雙組分BEC，必須滿足相分離條件才能誘導出調制不穩定性［28，29］.對于均勻條件下的自旋1超冷氣體，鐵磁凝聚體是動力學不穩定的，它會自發演化為多疇結構，與動力學穩定的反鐵磁凝聚體形成明顯差別［30-34］.人們也在自旋1/2系統中研究了帶SOC作用BEC的調制不穩定性［35-37］，發現不穩定性與無SOC作用BEC的結果有很大的不同.SOC項的加入極大地改變了BEC的不穩定性條件，使BEC的不穩定性不僅表現在具有吸引原子間的相互作用中，而且也表現在具有排斥性質的原子間相互作用中.同時，人們研究了調制不穩定性在自旋1 BEC中的推廣，并通過考慮密度-密度和自旋交換相互作用，揭示了系統更加豐富的不穩定結構［38］.最近，調制不穩定性在偶極量子氣體的BEC［39］和量子液滴系統中得到了研究［40，41］，使得人們對量子氣體的奇異狀態有了新的認識.

本文研究了拉曼耦合作用下具有自旋張量-動量耦合的自旋1 BEC的調制不穩定性質.在等效一維幾何模型中，利用平均場框架對調制不穩定性進行分析.結果表明，具有STMC和SOC作用自旋1 BEC的調制不穩定性表現出非平庸的性質，將導致系統中奇異的非線性激發和復雜動力學的出現.本文結構安排如下：

第一部分描述了具有STMC和SOC作用自旋1 BEC的理論模型.在第二部分中，通過連續波的線性穩定性分析，給出了調制不穩定性的理論分析過程，解析推導了擾動的頻率與波數之間的色散關系，并引入了不穩定性的增長速率，來定量地描述系統出現不穩定性的程度.在第三部分中，通過計算增長速率在動量空間的分布，討論了拉曼耦合和原子間有效相互作用對調制不穩定性的影響.通過與具有SOC作用的BEC在相同參數條件下的調制不穩定性進行比較，得到了一些新的結果.最后，在第四部分給出簡短的討論和本文的結論.

1?理論模型

本文的研究基于對超冷玻色氣體BEC中實現STMC的理論方案［18］.具有波數kR的三束激光在自旋1 BEC的三個超精細自旋態之間產生了兩個拉曼躍遷，兩個躍遷沿x方向具有相同的反沖動量2kR.在具有SOC的BEC中，兩個拉曼躍遷中沿x方向被轉移的反沖動量為±2kR［13］.這一過程使得具有STMC作用BEC的單粒子哈密頓量與具有SOC作用BEC的單粒子哈密頓量完全不同.具有STMC作用BEC的哈密頓量包括兩個亮態帶（與具有SOC作用自旋1/2 BEC相同）和一個暗態中間帶.中間帶最小值與兩個亮態的最小值非常接近，這能極大地改變系統的基態.超冷原子氣體中STMC效應與原子間的非線性相互作用相結合，為產生具有高對比度和長可調周期的新型動力學條紋相提供了機會［18］.

具有STMC作用自旋1 BEC的動力學由如下方程來給出［18，21］：

所有這些系數均由系統的初始密度以及參數ΩR和g來確定.

一般情況下，方程（10）的解析解是很難得到的，但是其數值解總是可以求解的.色散方程的解決定著系統調制不穩定的性質.本文發現對具有STMC的自旋1 BEC來說，色散方程具有六個不相同的根，代表了調制不穩定中六個不等價的分支.Ω虛部的存在性意味著連續波是調制不穩定的.空間調制微擾將隨著時間指數式增長.系統的不穩定增長率（IGR），定義為χm≡|Im（Ωm）|（m=1，2，3，4，5，6），給出調制不穩定程度的定量描述.顯然，調制不穩定增長率χm作為波數k的函數，可以被系統的參數ΩR和g進行調節.

3?主要結果

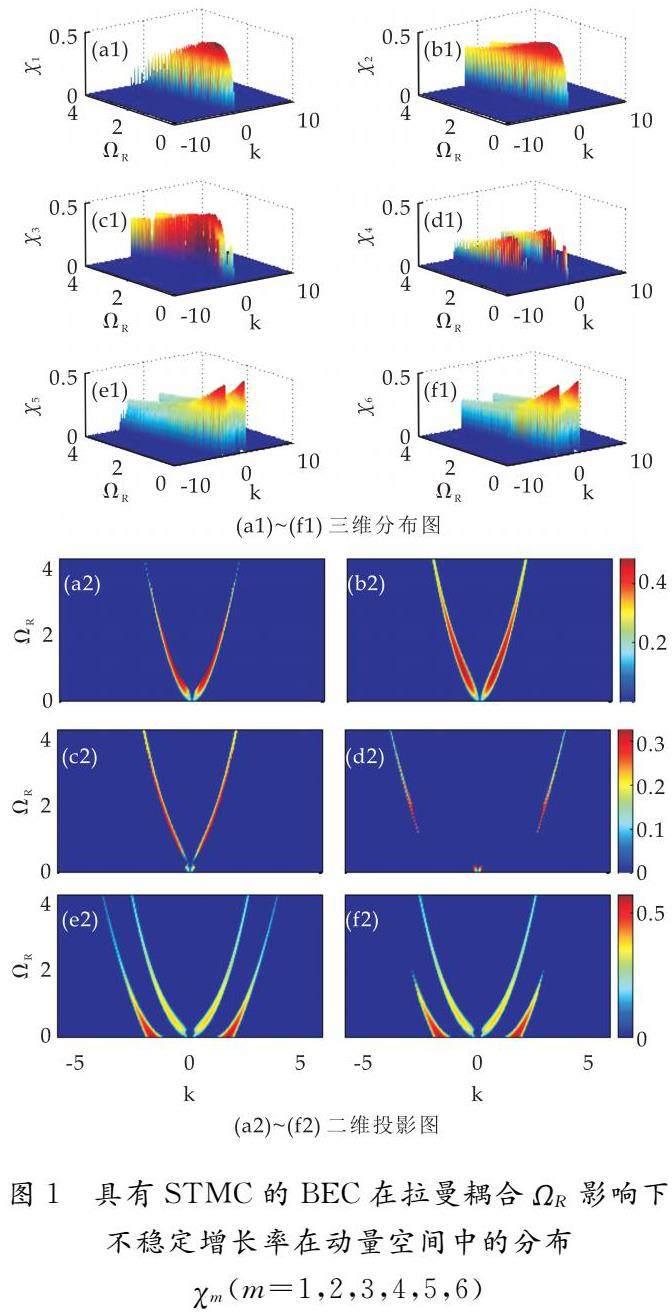
本部分給出本文的主要計算結果.圖1描述了固定原子間相互作用但改變拉曼耦合強度時，具有STMC作用BEC中連續波態的調制不穩定增長率χm在動量空間中的分布情況.原子間有效相互作用g=1.0.首先，本文發現動量空間中調制不穩定增長率關于k=0的分布是對稱的.在方程（9）形式的激發下，動量-k處基態的不穩定性與動量k處的不穩定性相伴隨出現并且具有相同的不穩定性質.±k處同時出現動量不穩定性表明該系統很容易產生條紋型的非線性激發.

圖1（a1）～（f1）所示的六種分布代表了六種不等價不穩定性分支.每個分支都具有雙峰或多峰結構.這六個分支中，每一個分支通過峰的強度和分布與其它分支相區別.為了表示方便，圖1（a2）～（f2）給出了三維分布對應的二維投影圖.在每個分支中，對給定的原子-原子間排斥相互作用強度（g>0），不穩定增長率在（k，ΩR）平面上的分布被分為數對不同的帶.

很明顯，在圖1（a2）～（d2）中，僅存在一對不穩定帶，而在圖1（e2）、（f2）中分別存在分布于k<0和k>0處的兩對不穩定帶.不同的對具有不同的分布和強度.不穩定性發生在整個拉曼耦合強度范圍（ΩR∈［0.5］），不穩定增長率隨著ΩR的增加而減小.當ΩR較大時，調制不穩定出現的時間會更長［24］.

為了進行比較，在相同參數條件下具有SOC作用自旋1 BEC的相應結果如圖2所示.可以看出，兩種情況下不穩定性的分布非常不同.對于SOC作用的BEC，在不穩定增長率χ1和χ2，χ3和χ4以及χ5和χ6的六種分布中，實際上只有三個不等價的分支.不僅如此，三個分支中不穩定帶的對數分別是1、3和4，說明具有STMC的BEC與具有SOC的BEC在調制不穩定性上有顯著差異.這種差異源于具有STMC和SOC作用BEC的單粒子哈密頓量中4ixF2z和4ixFz項所決定的不同對稱性.單粒子哈密頓量對STMC作用BEC具有自旋旋轉對稱性，對SOC作用BEC具有自旋旋轉和宇稱聯合對稱性［21］.拉曼耦合作用下的結果與圖1相似，不穩定性的強度隨著ΩR的增加而減小.

對于單組分BEC，調制不穩定性只存在于原子-原子間為吸引的相互作用系統中［26，27］.對于雙組分BEC，只要相分離條件滿足，則會出現不穩定性［28，29］.具有吸引相互作用的BEC（g<0）中更容易出現不穩定.圖3給出了考慮吸引原子間相互作用BEC連續波態的不穩定增長率χm（k，ΩR）的分布.原子間有效相互作用g=-1.0.研究發現，在具有STMC作用BEC的不穩定分布中，原子間的相互作用在吸引和排斥時存在較大的差異.在圖3中，前兩個分支的不穩定帶對數在圖3（a2）、（b2）中為1，在圖3（c2）、（d2）中為2，在圖3（e2）、（f2）中為3.不穩定增長率分布中，接近k=0的不穩定帶相比于具有排斥原子作用的情形更寬，意味著不穩定性更易發生在具有吸引相互作用的情形中.同時，吸引相互作用情形中更大的不穩定增長強度顯示不穩定將發生在相對更短的時間內.

在這種情況下，除了系統存在三個不同的分支外，圖4（a2）、（b2）給出的第一分支中不穩定帶的對數是1，圖4（c2）、（d2）描述的第二分支中不穩定帶的對數是3，圖4（e2）、（d2）中描述的第三個分支中不穩定帶的對數是5.最接近k=0的兩個分支比其它強度更大.無論如何，不管是具有STMC的BEC還是具有SOC的BEC，我們都有理由認為在相同條件下的吸引相互作用更有利于調制不穩定的出現.

圖5給出拉曼耦合強度ΩR=1.0時具有STMC作用BEC不穩定增長率χm（k，g）的分布.圖6給出了具有SOC作用BEC相似的結果.

結果顯示，具有STMC作用BEC的不穩定分布中存在6個不等價分支，而具有SOC作用BEC的不穩定分布中存在3個不等價分支.具有STMC作用BEC中除圖5（a）給出的第一個分支外，g<0情形下其它分支的條帶對數都大于g>0的情形，這從圖5（b）～（f）中可以看出.g<0時不穩定帶的強度隨著|g|的增加而增強.這一結果并不局限于k=0附近，而且可以拓展到更大的動量k.在圖6中，g>0和g<0時不穩定帶的對數相同，不穩定增長率的最大值隨著|g|的增加而急劇增加.

4?結論

綜上所述，本文對具有STMC作用自旋1 BEC的調制不穩定性進行了線性穩定性分析.系統的不穩定性質是由連續波的擾動色散關系決定的，連續波的不穩定性有六個不等價分支.對于每個分支，不穩定增長率在三維情況下的分布為雙峰或多峰結構，而在二維投影圖上則以一對或數對不穩定帶的形式表現出來.這些帶在零波數的兩側對稱分布.正動量和負動量同時出現不穩定表明，系統中具有條紋形狀的非線性結構易于激發.在相同的條件下，對具有SOC作用BEC的調制不穩定性進行了類似的研究.具有SOC作用BEC的調制不穩定分布實際上可以用三個不等價的分支來描述.多帶結構的不穩定分布會導致系統產生具有高次諧波的非線性激發和復雜動力學.對于具有STMC和SOC作用的BEC，在考慮拉曼耦合的整個區域內，調制不穩定性都會發生.不穩定強度隨著拉曼耦合強度的增加而減小，意味著調制不穩定發生時間隨著拉曼耦合強度的增加而變長.原子間相互作用越強，越容易觀測到調制不穩定性.無論是具有STMC還是具有SOC作用BEC，在同等條件下具有吸引相互作用要比排斥相互作用系統更有利于產生不穩定.上述結果反映了自旋1 BEC中由SOC和STMC以及原子間的相互作用誘導的調制不穩定的獨特性質，這些結果將促進對具有SOC和STMC作用BEC性能的進一步實驗研究.

參考文獻

［1］ Dalfovo F，Giorgini S，Pitaevskii L P，et al.Theory of Bose-Einstein condensation in trapped gases［J］.Review of Modern Physics，1999，71（3）：463-512.

［2］ Gross C，Bloch I.Quantum simulations with ultracold atoms in optical lattices［J］.Science，2017，357（6 355）：995-?1 001.

［3］ Chin C，Grimm R，Julienne P，et al.Feshbach resonances in ultracold gases［J］.Review of Modern Physics，2010，82（2）：1 225-1 286.

［4］ Kevrekidis P G，Frantzeskakis D J，Carretero Gonzalez R.Emergent nonlinear phenomena in Bose-Einstein condensates：Theory and experiment［M］.Verlag Berlin：Springer Publisher Services，2008.

［5］ Chen Q，Stajic J，Tan S，et al.BCS-BEC crossover：From high temperature superconductors to ultracold superfluids［J］.Physics Report，2005，412（1）：1-88.

［6］ Giorgini S，Pitaevskii L P，Stringari S.Theory of ultracold atomic fermi gases［J］.Review of Modern Physics，2008，80（4）：1 215-1 274.

［7］ Morsch O，Oberthaler M.Dynamics of Bose-Einstein condensates in optical lattices［J］.Review of Modern Physics，2006，78（1）：179-215.

［8］ Greiner M，Mandel O，Esslinger T，et al.Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms［J］.Nature，2002，415：39-44.

［9］ Jendrzejewski F，Bernard A，Muller K，et al.Three-dimensional localization of ultracold atoms in an optical disordered potential［J］.Nature Physics，2012，8：398-403.

［10］ Dalibard J，Gerbier F，Juzeliūnas G，et al.Artificial gauge potentials for neutral atoms［J］.Review of Modern Physics，2011，83（4）：1 523-1 543.

［11］ Cooper N R，Dalibard J，Spielman I B.Topological bands for ultracold atoms［J］.Review of Modern Physics，2019，91（1）：015 005.

［12］ Lin Y J，Jimenez Garcia K，Spielman I B.Spin-orbit-coupled Bose-Einstein condensates［J］.Nature，2011，471：83-86.

［13］ Campbell D L，Price R M，Putra A，et al.Magnetic phases of spin-1 spin-orbit-coupled Bose gases［J］.Nature Communications，2016，7：10 897.

［14］ Wang C J，Gao C，Jian C M，et al.Spin-orbit-coupled spinor Bose-Einstein condensates［J］.Physical Review Letters，2010，105（16）：160 403.

［15］ DeMarco M，Pu H.Angular spin-orbit coupling in cold atoms［J］.Physical Review A，2015，91（3）：033 630.

［16］ Sun K，Qu C，Zhang C.Spin-orbital-angular momentum coupling in Bose-Einstein condensates［J］.Physical Review A，2015，91（6）：063 627.

［17］ Chen H R，Lin K Y，Chen P K，et al.Spin-orbital-angular momentum coupled Bose-Einstein condensates［J］.Physical Review Letters，2018，121（11）：113 204.

［18］ Luo X W，Sun K，Zhang C W.Spin-tensor-momentum-?coupled Bose-Einstein condensates［J］.Physical Review Letters，2017，119（19）：193 001.

［19］ Hu H，Hou J P，Zhang F，et al.Topological triply degenerate points induced by spin-tensor-momentum couplings［J］.Physical Review Letters，2018，120（24）：240 401.

［20］ Zhao L C，Luo X W，Zhang C W.Magnetic stripe soliton and localized stripe wave in spin-1 Bose-Einstein condensates［J］.Physical Review A，2020，101（2）：023 621.

［21］ Sun J，Chen Y Y，Chen X，et al.Bright solitons in a spin-tensor-momentum-coupled Bose-Einstein condensate［J］.Physical Review A，2020，101（5）：053 621.

［22］ Zakharov V E，Ostrovsky L A.Modulation instability：The beginning［J］.Physica D：Nonlinear Phenomena，2009，238（5）：540-548.

［23］ Al Khawaja U，Stoof H T C，Hulet R G，et al.Bright soliton trains of trapped Bose-Einstein condensates［J］.Physical Review Letters，2002，89（20）：200 404.

［24］ Nguyen J H V，Luo D，Hulet R G.Formation of matter-wave soliton trains by modulational instability［J］.Science，2017，356（6 336）：422-426.

［25］ Everitt P J，Sooriyabandara M A，Guasoni M，et al.Observation of a modulational instability in Bose-Einstein condensates［J］.Physical Review A，2017，96（4）：041 601（R）.

［26］ Theocharis G，Rapti Z，Kevrekidis P G，et al.Modulational instability of Gross-Pitaevskii-type equations in 1+1 dimensions［J］.Physical Review A，2003，67（6）：063 610.

［27］ Salasnich L，Parola A，Reatto L.Modulational instability and complex dynamics of confined matter-wave solitons［J］.Physical Review Letters，2003，91（8）：080 405.

［28］ Kasamatsu K，Tsubota M.Multiple domain formation induced by modulation instability in two-component Bose-Einstein condensates［J］.Physical Review Letters，2004，93（10）：100 402.

［29］ Kasamatsu K，Tsubota M.Modulation instability and solitary-wave formation in two-component Bose-Einstein condensates［J］.Physical Review A，2006，74（1）：013 617.

［30］ Zhang W X，Zhou D L，Chang M S，et al.Dynamical instability and domain formation in a spin-1 Bose-Einstein condensate［J］.Physical Review Letters，2005，95（18）：180 403.

［31］ Pu Z G，Zhang J，Yi S，et al.Magnetic-field-induced dynamical instabilities in an antiferromagnetic spin-1 Bose-Einstein condensate［J］.Physical Review A，2016，93（5）：053 628.

［32］ Doktorov E V，Rothos V M，Kivshar Y S.Fulltime dynamics of modulational instability in spinor Bose-Einstein condensates［J］.Physical Review A，2007，76（1）：013 626.

［33］ Tasgal R S，Band Y B.Sound waves and modulational instabilities on continuous-wave solutions in spinor Bose-Einstein condensates［J］.Physical Review A，2015，91（1）：013 615.

［34］ Bhat I A，Mithun T，Malomed B A，et al.Continuous-?wave solutions and modulational instability in spinor condensates of positronium［J］.Journal of Physics B：Atomic，Molecular and Optical Physics，2018，51（4）：045 006.

［35］ Ozawa T，Pitaevskii L P，Stringari S.Supercurrent and dynamical instability of spin-orbit-coupled ultracold Bose gases［J］.Physical Review A，2013，87（6）：063 610.

［36］ Ahmad Bhat I，Mithun T，Malomed B A，et al.Modulational instability in binary spin-orbit-coupled Bose-Einstein condensates［J］.Physical Review A，2015，92（6）：063 606.

［37］ Bhuvaneswari S，Nithyanandan K，Muruganandam P，et al.Modulation instability in quasi two dimensional spin-orbit coupled Bose-Einstein condensates［J］.Journal of Physics B：Atomic，Molecular and Optical Physics，2016，49（24）：245 301.

［38］ Li G Q，Chen G D，Peng P，et al.Modulation instability of an spin-1 Bose-Einstein condensate with spin-orbit coupling［J］.Journal of Physics B：Atomic，Molecular and Optical Physics，2017，50（23）：235 302.

［39］ Ferrier Barbut I，Wenzel M，Schmitt M，et al.Onset of a modulational instability in trapped dipolar Bose-Einstein condensates［J］.Physical Review A，2018，97（1）：011 604（R） .

［40］ Otajonov S R，Tsoy E N，Abdullaev F K.Modulational instability and quantum droplets in a two-dimensional Bose-Einstein condensate ［J］.Physical Review A，2022，106（3）：033 309.

［41］ Mithun T，Maluckov A，Kasamatsu K，et al.Modulational instability，inter-component asymmetry，and formation of quantum droplets in one dimensional binary Bose gases［J］.Symmetry，2020，12：174.

［42］ Li D，Huang L，Peng P，et al.Experimental realization of spin-tensor momentum coupling in ultracold Fermi gases［J］.Physical Review A，2020，102（1）：013 309.

【責任編輯：陳?佳】

基金項目：國家自然科學基金項目（11405100）；陜西省科技廳自然科學基金項目（2020 JM-507，2019JM-332）；陜西科技大學博士科研啟動基金項目（2018BJ-02，2019BJ-58）; 西安交通大學城市學院校級研究專項（KCSZ01025）

作者簡介：李冠強（1983—），男，甘肅莊浪人，副教授，博士，研究方向：超冷原子物理、量子模擬、非線性物理與拓撲物理