立體幾何“動態”之折疊問題
■胥子伍
立體幾何中常求一些固定不變的點、線、面的位置關系,若給靜態的立體幾何問題賦予“活力”,滲透了“動態”的點、線、面元素,在點、線、面運動變化的幾何圖形中,探尋點、線、面的位置關系或進行有關角與距離的計算,立意會更新穎、更靈活,能很好地培養同學們的空間想象能力。
一、折疊之軌跡問題
例1如圖1,在正四棱錐S-ABCD中,E是BC的中點,點P在側面△SCD內及其邊界上運動,并且總是保持PE//平面SBD。
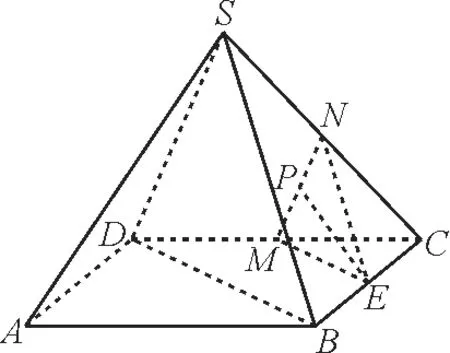
圖1
則動點P的軌跡與△SCD組成的相關圖形最有可能是( )。
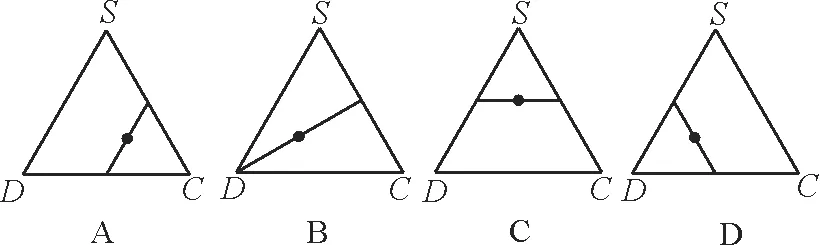
解:分別取CD,SC的中點M,N。
因為E是BC的中點,所以EM//BD,EN//SB。因為EM,EN?平面SBD,BD,SB?平面SBD,所以EM//平面SBD,EN//平面SBD。
又因為EM∩EN=E,EM,EN?平面EMN,所以平面EMN//平面SBD,所以當P在線段MN上移動時,PE?平面EMN,此時能保持PE//平面SBD,則動點P的軌跡與△SCD組成的相關圖形符合選項A。應選A。
點評
變量的變化引發空間位置關系的變化,將一些變化的線與角合理轉化,集中到一個平面內,則可將空間的“動態”問題轉化為平面的“動態”問題,再利用平面幾何知識加以解決。本題利用線面平行、面面平行,在動態問題中提煉一些不變的“靜態”的量,建立“不變量”與“動點”之間的關系,從而確定動點的軌跡。
二、折疊之范圍問題
例2在如圖2 所示的長方形ABCD中,AB=2,BC=1,E為DC的中點,F為線段EC(端點除外)上一動點。現將△AFD沿AF折起,使平面AFD⊥平面ABCF,得到如圖3所示的四棱錐。在平面ABD內過點D作DK⊥AB,垂足為K。設AK=t,則t的取值范圍是_____。
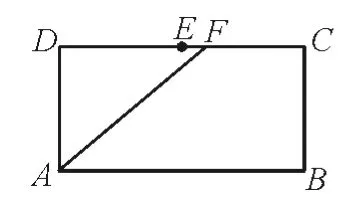
圖2
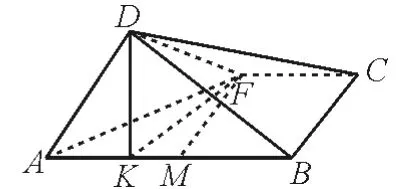
圖3
解:過點F作FM⊥AB,交AB于點M。設FC=x,0<x<1,則MF=BC=1,MB=FC=x。易知AK<AD=1。因為AB=2,所以點K一定在點M的左邊,則MK=2-t-x。在Rt △ADK中,DK2=1-t2,在Rt△FMK中,FK2=1+(2-t-x)2。

點評
“動”與“靜”是相對的,在運動變化過程中,要善于尋找或構造與之相關的一些不變因素,建立變量與不變量的有機統一體。本題是一個動態的翻折問題,需要同學們發現其中不變的垂直關系,從而得出相關變量間的關系,最終轉化成函數的值域問題求解。
三、折疊之最值問題
例3設矩形ABCD(AB>BC)的周長為定值2a,把△ABC沿AC向△ADC折疊,AB折過去后交DC于點P,如圖4,則下列說法正確的是( )。

圖4
A.矩形ABCD的面積有最大值
B.△APD的周長為定值
C.△APD的面積有最大值
D.線段PC有最大值


點評
一般地,位于“折痕”同側的點、線、面間的位置和數量關系不變,而位于“折痕”兩側的點、線、面間的位置關系會發生變化;對于不變的關系應在平面圖形中處理,而對于變化的關系則要在立體圖形中解決。
感悟與提高
已知菱形ABCD的邊長為1(如圖5),∠BAD=60°,對角線AC與BD交于點O。將菱形ABCD沿對角線BD折成平面角為θ的二面角(如圖6),若θ∈[60 °,120°],則折后點O到直線AC距離的最值是( )。
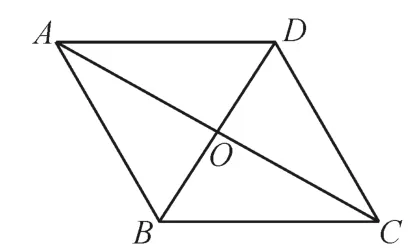
圖5

圖6


