聚焦立體幾何中的動態(tài)問題
■童昌立
立體幾何的動態(tài)問題的實質(zhì)是數(shù)學建模問題,解這類問題,需要有較強的空間想象能力和化歸處理能力。對于動態(tài)立體幾何問題,如果能努力探尋運動過程中“靜”的一面,動中求靜,往往能以靜制動。
題型1:截面問題
例1如圖1,用一個平面去截直三棱柱ABCA1B1C1,分別交A1C1,B1C1,BC,AC于點E,F,G,H。若A1A>A1C1,則截面的形狀可以為____。(把你認為可能的結(jié)果的序號填在橫線上)

圖1
①一般的平行四邊形,②矩形,③菱形,④正方形,⑤梯形。
解析
由ABC-A1B1C1為直三棱柱,可知平面A1B1C1//平面ABC。因為截面過平面A1B1C1、平面ABC,所以交線EF//HG。當FG不與B1B平行時,此時截得的EH不平行于FG,則四邊形EFGH為梯形;當FG//B1B時,此時截得的EH//FG,且FG⊥EF,則四邊形EFGH為矩形。答案為②⑤。
點評
熟記平面圖形的性質(zhì)是解題的關(guān)鍵。
題型2:角度問題
例2設異面直線a,b所成的角為30°,經(jīng)過空間一點O有且只有兩條直線與異面直線a,b成等角θ,則θ的取值范圍為_____。
解析
如圖2,過O作a1//a,b1//b,則a1,b1所成的角,即為異面直線a,b所成的角。
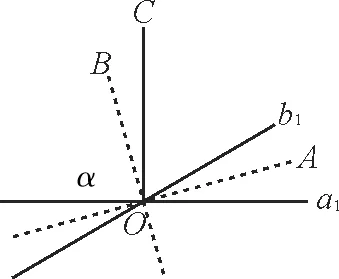
圖2
記a1,b1確定一個平面為α,過O作OC⊥α,過O作直線OA和直線OB分別平分a1,b1形成的兩個對頂角。
當過O的直線在平面AOC內(nèi)旋轉(zhuǎn)時,與a1,b1所成的角為θ,且15°≤θ≤90°;當過O的直線在平面BOC內(nèi)旋轉(zhuǎn)時,與a1,b1所成的角為θ,且75°≤θ≤90°。
結(jié)合對稱性可知,若經(jīng)過空間一點O有且只有兩條直線與異面直線a,b成等角θ,則θ的取值范圍為15°<θ<75°。
點評
兩條異面直線所成角的范圍是0°<θ≤90°。
題型3:平行問題
例3如圖3所示,在正四棱柱ABCDA1B1C1D1中,E,F,G,H分別是棱CC1,C1D1,D1D,DC的中點,N是BC的中點,點M在四邊形EFGH及其內(nèi)部運動,則點M只需滿足條件_____時,就有MN//平面B1BDD1。(請?zhí)钌夏阏J為正確的一個條件即可,不必考慮全部可能情況)
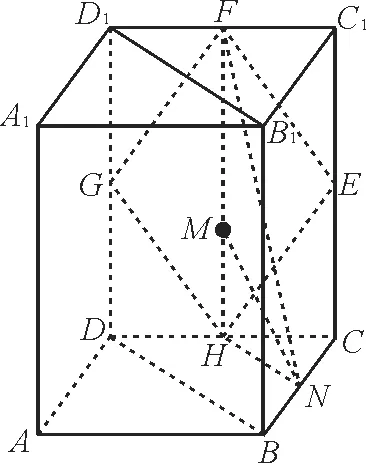
圖3
解析
由題意得FH//DD1,HN//BD,FH∩HN=H,DD1∩BD=D,所以平面FHN//平面B1BDD1。只需M∈FH,則MN?平面FHN,這時MN//平面B1BDD1。
故滿足條件的點M在線段FH上(或點M與點H重合)。
點評
本題屬于開放性問題,解題的關(guān)鍵是證明MN//平面B1BDD1。
題型4:垂直問題
例4如圖4所示,在棱長為1的正方體ABCD-A1B1C1D1中,點E是 棱BC的 中點,點F是棱CD上的動點。試確定點F的位置,使得D1E⊥平面AB1F。
解析
當點F為CD的中點時,D1E⊥平面AB1F。
因為A1B⊥AB1,A1D1⊥AB1,又A1D1∩A1B=A1,所以AB1⊥平面A1BCD1。因為D1E?平面A1BCD1,所以AB1⊥D1E。
因為DD1⊥平 面ABCD,所 以DD1⊥AF。又AF⊥DE,所以AF⊥平面D1DE,所以AF⊥D1E。又AF∩AB1=A,所以D1E⊥平面AB1F。故當點F是CD的中點時,D1E⊥平面AB1F。
點評
本題主要考查線面垂直的判定與性質(zhì)。探求滿足條件的點的問題,一般可考慮特殊情況,如線段的中點,三等分點等。
題型5:軌跡問題
例5如圖5,已知線段AB垂直于定圓O所在的平面,B,C是☉O上的兩個點,H是點B在AC上的射影,當點C運動時,點H運動的軌跡是( )。

圖5
A.圓 B.直線 C.線段 D.三角形
解析
過點B作☉O的直徑BD,連接CD,AD,則BC⊥CD。
過點B作BE⊥AD于點E,連接EH。因為AB⊥平面BCD,所以AB⊥CD。因為BC⊥CD,且AB∩BC=B,所以CD⊥平面ABC,所以CD⊥BH。
又BH⊥AC,且AC∩CD=C,所以BH⊥平面ACD,所以BH⊥AD,BH⊥HE。
注意到過點B與直線AD垂直的直線都在同一平面內(nèi),于是結(jié)合點B,E的位置,可知當點C運動時,點H的運動軌跡是以BE為直徑的圓。應選A。
點評
立體幾何中的軌跡問題,涉及的知識點較多,需要熟記直線、圓、球等幾何圖形的性質(zhì)。
感悟與提高

圖6


