巧借“補(bǔ)形”思維，妙解立體幾何問題

■孫海鷹

利用“補(bǔ)形”思維這一橋梁,可以使數(shù)學(xué)的思維方法更加活躍、簡(jiǎn)捷,應(yīng)用起來更加靈活、多樣,能有效培養(yǎng)同學(xué)們思維的靈活性、獨(dú)創(chuàng)性。利用“補(bǔ)形”思維可以把空間立體幾何中的一些不規(guī)則形體、不熟悉形體、殘缺形體補(bǔ)成相應(yīng)的規(guī)則形體、熟悉形體、完整形體等,對(duì)解決問題起到化繁為簡(jiǎn)、一目了然的作用,使得數(shù)學(xué)思維更加靈活,數(shù)學(xué)知識(shí)結(jié)構(gòu)更加完整、充實(shí),數(shù)學(xué)思想方法更加完美。

一、還原補(bǔ)形法

例1為了給數(shù)學(xué)家帕西奧利的《神圣的比例》畫插圖,列奧納多·達(dá)·芬奇繪制了一些多面體,圖1 所示的多面體就是其中之一。它是由一個(gè)正方體沿著各棱的中點(diǎn)截去八個(gè)三棱錐后剩下的部分,這個(gè)多面體的各棱長(zhǎng)均為2,則該多面體外接球的體積為( )。

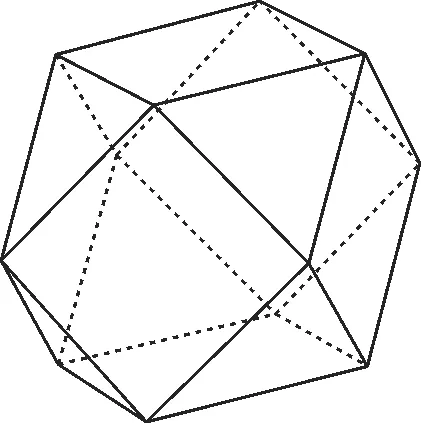
圖1

A.16π B.8π

分析：對(duì)于此類空間立體幾何中的不規(guī)則形體——多面體,直接處理起來有較大的難度,可借助空間幾何體的還原補(bǔ)形法,把該多面體進(jìn)行還原補(bǔ)形為正方體,結(jié)合補(bǔ)形前后對(duì)應(yīng)圖形中相關(guān)元素的位置關(guān)系與變化情況,進(jìn)行合理分析與運(yùn)算。

解：結(jié)合圖1,把該多面體進(jìn)行還原補(bǔ)形為正方體,如圖2所示。

圖2

點(diǎn)評(píng)

還原是回歸問題本質(zhì)的一種邏輯推理方式。在解決一些空間幾何體問題中,合理回歸,完整地進(jìn)行還原與補(bǔ)形是解題的關(guān)鍵。在處理空間幾何體的還原補(bǔ)形時(shí),要注意回歸的簡(jiǎn)單幾何體與“補(bǔ)”上去的小幾何體之間要素的聯(lián)系與圖形之間的變化,正確構(gòu)建相互之間的關(guān)系,不要出現(xiàn)添加或遺漏。

二、聯(lián)系補(bǔ)形法

例2已知正三棱錐P-ABC,點(diǎn)P,A,B,C都在半徑為3的球面上,若PA,PB,PC兩兩相互垂直,則球心到截面ABC的距離為_____。

分析：此類不同空間幾何體間(正三棱錐與球)的聯(lián)系問題,需要進(jìn)行合理補(bǔ)形,將正三棱錐與球這兩種不同的空間幾何體聯(lián)系在一起,使得問題的處理直觀易懂,從而便于分析與計(jì)算。

解：由于正三棱錐的側(cè)棱PA,PB,PC兩兩互相垂直,故以PA,PB,PC為棱補(bǔ)成正方體,如圖3所示。

圖3

球心O為正方體的體對(duì)角線PD的中點(diǎn),且PO= 3,則正方體的棱長(zhǎng)為2。

點(diǎn)評(píng)

尋找聯(lián)系是構(gòu)建不同數(shù)學(xué)元素之間的橋梁。在空間立體幾何問題中,抓住不同空間幾何體之間的聯(lián)系,合理補(bǔ)形(如三條側(cè)棱兩兩互相垂直,可補(bǔ)形為正方體或長(zhǎng)方體),使得問題更加直觀易求。

三、對(duì)稱補(bǔ)形法

例3如圖4所示,在斜截圓柱中,已知圓柱的底面直徑為40cm,母線最短與最長(zhǎng)的分別為50cm,80cm,則該斜截圓柱的體積V=____。

圖4

分析：此類空間幾何體中的殘缺形體,屬于不太規(guī)則的空間幾何體,直接求解無從下手,可借助空間幾何體的幾何特征進(jìn)行合理的對(duì)稱補(bǔ)形,將題設(shè)條件中的斜截圓柱按斜截面吻合對(duì)接,補(bǔ)全為一個(gè)完整的圓柱,再利用圓柱的體積公式求解。

解：將題設(shè)條件中的斜截圓柱按斜截面吻合對(duì)接,補(bǔ)全為一個(gè)完整的圓柱(即斜截圓柱進(jìn)行翻轉(zhuǎn)對(duì)接)。

點(diǎn)評(píng)

對(duì)稱是數(shù)學(xué)中的一種重要關(guān)系,也是充分展示數(shù)學(xué)美的一種表現(xiàn)形式。在解決空間幾何體問題時(shí),對(duì)于一些特殊的殘缺形體,要善于發(fā)現(xiàn)圖形中的對(duì)稱關(guān)系與幾何特征,借助相同圖形之間的對(duì)稱補(bǔ)形法進(jìn)行化歸與轉(zhuǎn)化,對(duì)空間想象能力的提升很有幫助。

編者的話：“補(bǔ)形”思維解決立體幾何問題,是整體思想的一種具體體現(xiàn),可將不規(guī)則的、陌生的、復(fù)雜的幾何體補(bǔ)成規(guī)則的、熟悉的、簡(jiǎn)單的幾何體(如常見的長(zhǎng)方體、正方體、平行六面體、圓柱等),在所補(bǔ)成的空間幾何體中研究原幾何體的有關(guān)元素的位置關(guān)系、空間角或空間距離的計(jì)算等,從而實(shí)現(xiàn)問題的順利解決。這類問題,能全面考查數(shù)學(xué)基礎(chǔ)知識(shí)、基本技能、基本思想、基本活動(dòng)經(jīng)驗(yàn)這“四基”的落實(shí)情況,以及發(fā)現(xiàn)問題、提出問題、分析問題和解決問題能力的培養(yǎng)與提升。

感悟與提高

若三棱錐P-ABC中最長(zhǎng)的棱PA=2,且各面均為直角三角形,則此三棱錐外接球的體積是_____。

提示:根據(jù)題意,可把該三棱錐補(bǔ)成長(zhǎng)方體,如圖5 所示,則該三棱錐的外接球即為該長(zhǎng)方體的外接球。易得外接球的半徑,所以該三棱錐外接球的體積

圖5