基于星間鏈路的星座相對構型保持方法

楊盛慶，吳敬玉，朱文山，鐘超

1．上海航天控制技術研究所，上海 201109

2．上海市空間智能控制技術重點實驗室，上海 201109

隨著航天科學技術的發展，航天任務日趨復雜。傳統的大衛星受自身軌道運動和地球自轉運動造成的時空約束，單個衛星難以實現全球性的實時觀測或通訊功能，小衛星星座應運而生。隨著小衛星發射入軌和全球組網成本的降低，國外SpaceX、OneWeb、亞馬遜等商業航天公司都相繼提出了低軌星座計劃，通過低軌巨型星座提供全球覆蓋的寬帶通信服務[1］。

星座的種類繁多，根據功能不同，有通訊、導航、測繪等。根據所處軌道劃分，有靜止軌道[2］、傾斜中軌道、大橢圓軌道[3］、近地極軌道[4］等。星座發展的初期，研究內容主要針對星座的軌道設計，設計目標包括星座的構型最優[5-6］、星座的覆蓋特性最優等[7-8］。在星座構型確定的基礎上進行星座構型保持，首先需要解明航天器在自然受攝狀態下的相對運動特征。文獻[9］研究了地球非球形引力攝動下，各航天器初值偏差引起的星座構型演化問題。文獻[10］基于線性化的相對運動方程，實現了J2項攝動作用下近距離星座的相對運動控制。文獻[11］針對地球非球形引力攝動，提出了主動偏置半長軸和傾角來補償升交點赤經和沿跡角漂移量的方法。大氣阻力是影響近地航天器運動的一項重要攝動項，大氣阻力的積累效果會致使軌道衰減，改變航天器的軌道角速度。星座內航天器由于面質比的差異，所受大氣阻力的攝動影響存在差異，會導致軌道面內的平均半長軸產生偏差，進而使航天器之間的相位差偏離標稱值。文獻[12-13］分析單個航天器軌道在大氣阻力影響下的變化特性，提出通過改變航天器迎風面，進行同一圓軌道上2 個航天器之間的相位調整。此外，雖然日月引力攝動屬于保守力，但對中高軌道和太陽同步軌道的影響較為明顯。日月引力攝動的長期積累，會產生軌道傾角的偏差。文獻[14］針對中高軌道上的Walker 星座所受的各項攝動，研究了星座構型的攝動補償法，提出了星座構型數值微分修正法。文獻[15］針對低軌大規模Walker 星座構型設計了一套控制仿真系統。綜上所述，航天器在軌受攝運動復雜，軌道面內和軌道面外運動存在耦合。

星座構型保持是一個復雜的多體運動控制問題，需要設計合理高效的軌道控制策略。一般來講，星座軌道面內的相對構型保持主要處理面質比差異導致的平均半長軸差異和相位差漂移。星座軌道面外相對構型保持主要處理地球非球型引力、大氣阻力、日月引力攝動聯合引起的軌道面長期變化。文獻[16］提出星座的構型保持可以采用絕對位置保持或相對構型保持控制策略。絕對位置保持要求單星的星下點軌跡按嚴格固定的網格運行，單星位置保持在隨星座構型一起運動的控制盒內，通過絕對位置的保持來實現星座構型保持。文獻[17］提出使用公開的兩行軌道根數對國外星座控制策略進行分析，重點分析了銥星、一網、星鏈星座的控制規律。文獻[18-19］采用網格分割的方法，提出了基于絕對位置保持的Walker 星座和玫瑰星座構型保持方法。絕對位置保持具有控制方法簡單的特征，但是絕對位置保持的目標狀態難以在星上自主確定，需要地面輔助確定絕對位置保持的目標軌道。而且，絕對位置保持的星座構型剛性強，控制需要完全補償大氣阻力導致的星座軌道衰減，相應的控制代價更大。與之相反，相對構型保持理論上僅需補償面質比差異導致的衰減偏差，能夠使星座中所有航天器趨同于一致的速率衰減，從而減少控制代價。

星座相對構型保持的核心問題，是要構造一類基于局部測量信息的控制方法。基于局部鏈路的巨型星座構型保持屬于分布式控制方法，相較于星座的整體優化方法（集中式控制，優化變量多、計算代價大），分布式控制更有利于在軌自主保持的實現。一致性控制方法能夠根據需求，兼容集中式或分布式控制，較好地實現多個體系統的協同控制，已應用到多個航天器的編隊協同[20］和姿態協同控制[21］。文獻[22］基于星座內航天器相對運動，介紹了十字型、星型鏈路的星座構型特征。利用圖論刻畫多個體系統拓撲結構并應用一致性控制方法，是實現星座相對構型保持控制的一種有效手段。文獻[23-24］分別結合航天器和導彈力學系統，利用拓撲結構設計了多體系統的分布式協同控制方法。不同于局部的平面拓撲，星座構成一個閉環的網絡，閉環星座的拓撲結構及其一致性控制有效性仍有待進一步研究。星座的軌道多要素聯合保持控制，屬于多參數耦合的非線性動力學系統，還要考慮動力學系統的高階形式[25］。為了提升高階一致性的控制效率，文獻[26］介紹了一種基于PID 控制參數設計的一致性控制方法。本文針對自然攝動下軌道運動特性，提出了星座相對構型保持的一致性控制方法。考慮到攝動導致的相對運動變化率較小，為了便于工程應用，可以考慮采用定周期控制，將相對構型保持控制轉變為一個離散一致性控制問題[27-28］。

本文針對低軌巨型星座，分析了星座多個體系統不同的星間鏈路連接方式及其閉環網絡特征，提出了不同幾何拓撲結構及其相應的圖論構造方法。針對航天器的受攝運動特征，分析了巨型星座軌道面內平均半長軸和相位差的漂移情況。針對星座內航天器平均半長軸和相位差變化的特征，構造了相應的離散二階一致性控制算法。

1 星座的幾何拓撲結構與鏈路圖

1.1 星間鏈路的幾何拓撲結構

星座的相對構型保持可視為多星系統的一致性控制，考慮到建立星間鏈路的空間約束和效費比，假設只在軌道面內的相鄰衛星和相鄰軌道面之間的“鄰位”衛星之間建立星間鏈路，每顆衛星獲取的群體信息是局部的。對于確定構型的星座，相鄰衛星和“鄰位”衛星之間的相位控制目標是明確的。

星間鏈路的有效距離，以過地心大圓的相位差形式表述

式中：Re表示地球半徑；a表示衛星軌道的半長軸；ΔM表示星間的平近點角之差。以軌道高度540 km 的軌道為例，能夠建立星間鏈路的最大相位差為45°。使用下標表示衛星編號，相鄰衛星間的相對升交點赤經ΔΩij和相對緯度幅角Δuij取值ΔΩij≈Δuij≈40o，形成如圖1 所示的十字型鏈路星座。星座共計81 個航天器，包含9 個軌道面，每個軌道面內9 個航天器，相鄰航天器的相位差40°，相鄰軌道面之間“鄰位”航天器的相位差為40°。圖中對航天器進行了編號，整個星座形成閉環的網絡。通過標識圖形形狀、標色和編號聯合，來區分圖中形成閉合圖的邊界和頂點的情況。藍色正方形表示軌道面內形成閉環的邊界航天器、綠色菱形表示不同軌道面形成閉環的邊界航天器、六邊形為2 個邊界的交點航天器。

圖1 星座的十字型鏈路拓撲結構Fig.1 Constellation topology with cruciform structure links

取ΔΩij≈20o，航 天 器i和 航 天 器j位 于 相 鄰軌道面時Δuij≈20o，航天器i和航天器j位于同一軌道面時Δuij≈40o。星座共計162 個航天器，包含18 個軌道面，每個軌道面內9 個航天器，相鄰航天器的相位差40°，相鄰軌道面之間“鄰位”航天器的相位差為20°。根據星間鏈路的不同建立方式，可以定義叉字型鏈路（如圖2 所示）和星型鏈路的星座（如圖3 所示），航天器標示的圖形形狀、標色和編號原則同上文。

圖2 星座的叉字型鏈路拓撲結構Fig.2 Constellation topology of cross structure links

圖3 星座的星字型鏈路拓撲結構Fig.3 Constellation topology with star structure links

1.2 基于幾何拓撲結構的局部鏈路圖

使用局部鏈路圖描述星座的幾何拓撲結構，且默認建立星間鏈路的航天器的信息鏈路雙向傳遞。如圖4 所示，建立星座的局部拓撲結構。其中，星型鏈路根據局部的相對位置關系可以定義左側軌道面上方/下方、相同軌道面上方/下方、右側軌道面上方/下方。

圖4 星座的局部拓撲結構Fig.4 Local topology of constellation

假設星座共計N個軌道面，每個軌道面內M個航天器。為了建立拓撲結構對應的Laplacian矩陣，需要對星座內航天器進行編號。定義軌道面序號和軌道面內序號組合(n，m)到一維計數的映射f：(n，m)→k，滿足k=(n-1)M+m。

同理，定義g：k→(n，m)，滿足

具有星間鏈路的航天器之間

觀察到星座的拓撲結構中，形成閉環結構的共用點特征，需要對邊界進行特殊處理。

對于軌道面序號

利用上述局部拓撲構造方法和航天器編號規則分析圖3 所示的星型鏈路星座，圖5 為該星座內部的鏈路狀態，是Laplacian 矩陣的圖形化表述，展示了巨型星座中局部鏈路的稀疏性。圖中鏈路狀態為1 表示具備星間鏈路，0 表示不具備星間鏈路。表1 為該星座中局部鏈路的示例。

圖5 星字型星座的鏈路狀態Fig.5 Inter-satellite connections in star structure constellation

表1 星字型星座內鏈路示例Table 1 Examples of inter-satellite connections in star structure constellation

根據上述編號規則，生成Laplacian 矩陣，并計算相應的矩陣特征值。如圖6 所示，不同拓撲結構的Laplacian 矩陣，隨著星間鏈路數量的增加，特征值負數根在絕對值大的區域分布更加密集，多個體系統的一致收斂性更好。

圖6 不同拓撲結構的Laplacian 矩陣特征值Fig.6 Eigenvalues of Laplacian matrix for different topology structures

2 星座的相對構型保持

2.1 軌道的動力學方程

低軌衛星在軌運動主要受到地球引力場、日月引力、大氣阻力等攝動影響。由J2項攝動、大氣阻力引起的平均軌道根數的長期變化率為

式中：e為偏心率；i為軌道傾角；Ω為升交點赤經；ω為近地點幅角；M為平近點角；n為軌道角速度；J2為引力場J2項參數；CD為大氣阻力參數；A為航天器迎風面積；m為航天器質量；ρ為大氣密度。軌道面內的星座構型保持主要針對軌道根數的平均半長軸和平近點角，針對星座內航天器面內構型產生的長期漂移的根源，即大氣阻力和面質比差異導致的軌道衰減速率、軌道角速度不一致，控制平均軌道半長軸可以實現星座軌道面內的構型保持。

2.2 星座相對構型保持的一致性控制

多個體系統的二階一致性控制，其一般形式可以描述為[25］

式中：ξi表示個體i運動的狀態量；ζi表示個體i運動的一階狀態量；gij為多個體系統之間的關聯參數；kij為一致性控制算法中不同鏈路對應的控制調節參數。

軌道面內的星座的構型保持控制以平均半長軸和平近點角作為控制的狀態量，要求控制目標實現平均半長軸的一致、實現平近點角的目標狀態一致。

式中：ΔM*ij根據星座拓撲情況定義。以星型鏈路星座為例，ΔM*ij取值為±20o和±40o。考慮到拓撲結構的幾何對稱性，假設控制參數取常值kij=k時，

軌道面內的星座構型保持，可以轉化為二階一致性控制

式中，參數γ的合理確定是實現二階一致性控制的關鍵。式（9）可轉化為

利用泰勒展開

工程實踐中，控制往往采用定周期控制形式。構造二階一致性控制的離散形式[27］

3 數值實驗

3.1 星座構型的受攝運動

數學實驗采用軌道高度為540 km 的太陽同步軌道，星座采用162 個航天器組成的星字型鏈路構型。采用上文所述編號方式，軌道面1 的降交點地方時取0 時，后續軌道面均勻分布。每個軌道面內第1 個航天器的緯度幅角根據幾何拓撲結構定義，取值為

使用MATLAB 驅動軌道積分器進行巨型星座的軌道積分，如圖7 所示。積分器采用式（5）所述的軌道動力學和四階龍格庫塔積分算法，軌道積分器的接口函數中軌道位置相關輸入項為平近點角，需要由緯度幅角轉換為平近點角。

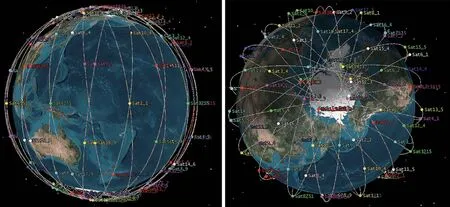
圖7 星座的三維視圖Fig.7 Three dimensional vision of constellation

模擬星座實際在軌存在的面質比差異，以0.005 m2/kg 為基準面質比。如表2 所示，針對軌道面序號和軌道面內序號組合(n，m)生成隨機數，使得每個航天的面質比在基準面質比的基礎之上，進行±20%的浮動變化。大氣密度隨著太陽活動的低年、中年或高年特征而變化。

表2 基準面質比基礎之上的星間差異Table 2 Difference between satellites based on typical mass-area ratio

根據文獻[29］所述大氣密度表，采用太陽活動中年的大氣密度為基準，對軌道高度進行擬合插值得到540 km 軌道高度的平均大氣密度，約為ρ=7.2×10-13kg/m3。取CD=2.2，根據式（5）中半長軸的變化率公式，該軌道上航天器的平均半長軸日衰減約36 m。軌道受攝運動90 天，星間半長軸偏差累積量最大值達到1 000 m，平近點角偏差累積量最大值達到60°，如圖8和圖9所示。

圖8 大氣阻力下自由漂移90 天的平近點角偏差Fig.8 Relative mean anomaly axis excursion in 90 days with air drag

圖9 大氣阻力下自由漂移90 天的半長軸偏差Fig.9 Relative semi-major axis excursion in 90 days with air drag

本文中二階一致性控制仿真采用沖量式控制。根據高斯攝動方程，對于半長軸的控制，連續推力的弧段積累就能基本實現沖量式控制的等效效果。連續推力和沖量式控制的區別在于對偏心率矢量的影響。工程應用中，可以考慮定周期時間點附近的特殊點對稱弧段實施連續推力控制，避免或減小連續推力對偏心率矢量產生的弧段效應。

3.2 星座構型的一致性控制效果

仿真驗證星座構型的一致性控制效果，定周期控制的間隔設置為1 天，仿真90 天。設置控制參數設置(k，γk)=(0.2，6 000)。基于星座相對構型保持的一致性控制，星間半長軸偏差控制在( -5 m，5 m)范圍內，平近點角偏差控制在標稱值附近( -0.1o，0.1o)范圍內，如圖10 和圖11 所示。相對構型保持控制主要消除面質比差異導致的衰減不一致，并非完全補償大氣阻力造成的軌道衰減。如圖12 所示，星座中162 顆衛星以1 天1 次的控制頻率進行半長軸調整，離散一致性控制過程中的控制代價以半長軸控制量形式表述。每顆星的控制量與其面質比相關，控制趨于穩定后，半長軸形式的控制量均＜10 m。相較于絕對位置保持補償平均半長軸36 m 日衰減量，相對構型保持的控制代價更小。

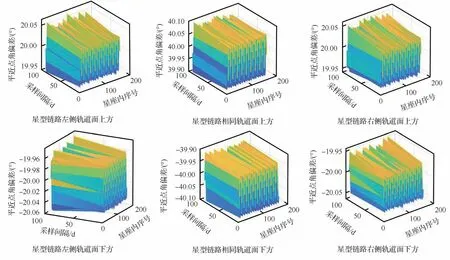
圖10 相對構型保持控制下90 天的平近點角偏差Fig.10 Relative mean anomaly axis in 90 days with relative-configuration maintenance

圖11 相對構型保持控制下90 天的半長軸偏差Fig.11 Relative semi-major axis in 90 days with relative-configuration maintenance

圖12 星座相對構型保持的控制量統計（半長軸控制量形式）Fig.12 Statistics on control cost of relative configuration maintenance in forms of semi-major axis

4 結 論

巨型星座中航天器受空間攝動作用，星座構型長期演化會造成偏差累積漂移現象，需要進行星座構型保持控制。傳統的絕對位置保持方法，星上難以匯集星座整體信息以生成目標軌道，必須由地面介入規劃。隨著星座規模的日趨擴大，未來星座構型保持的發展方向將圍繞基于局部信息的分布式相對構型保持方法。相較于傳統的絕對位置保持方法補償軌道衰減，相對構型保持只需補償面質比差異造成的衰減差異，控制代價更小。

星座在空間中形成一個閉環的拓撲結構，根據星間鏈路的連接情況，本文提出了不同幾何拓撲結構及其相應的圖論構造方法。針對星座軌道面內航天器平均半長軸和相位差變化的特征，構造了相應的離散二階一致性控制算法。后續工程應用，需要高精度軌道根數瞬平轉換算法來保障半長軸的確定精度或者使用相對相位的漂移量估計星間的半長軸偏差。此外，星座構型保持面臨軌道面內運動的相對半長軸和相對相位保持、軌道面外運動的相對升交點赤經保持等問題。由于日月引力對軌道傾角的長期項和周期項影響，結合J2項導致軌道面內運動、軌道面外運動的耦合特性，其力學問題的解析形式仍有待進一步研究。其本質是控制對象的動力學復雜度提升，本文闡述的星座拓撲結構和二階一致性控制方法仍可沿用。