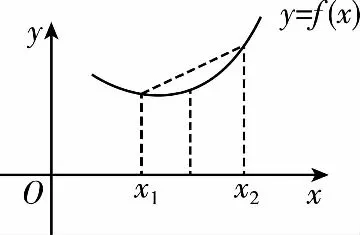
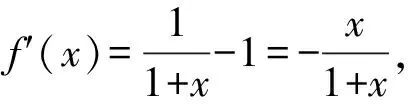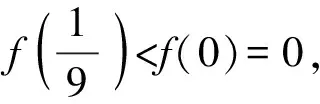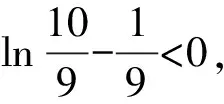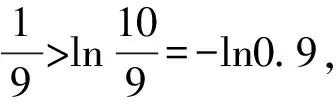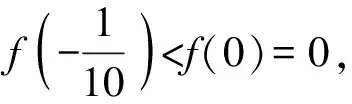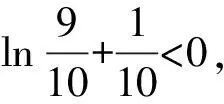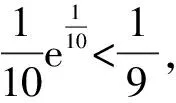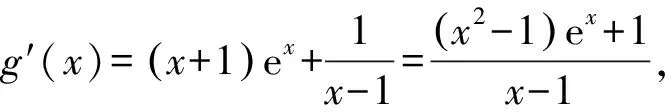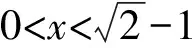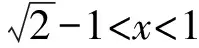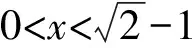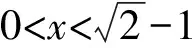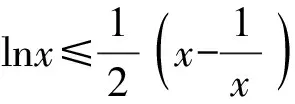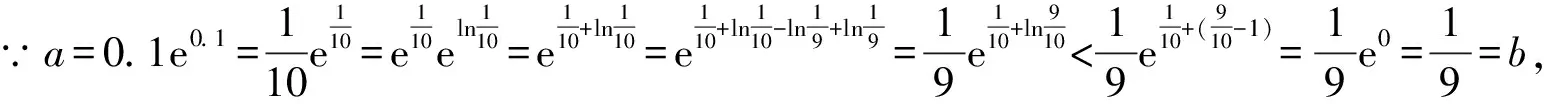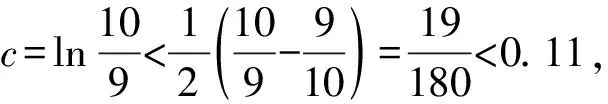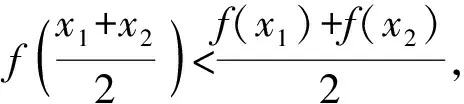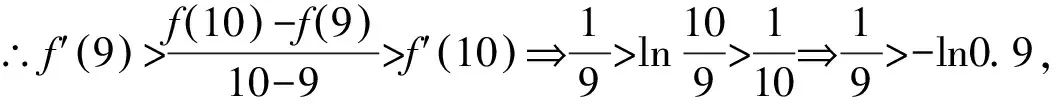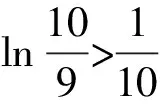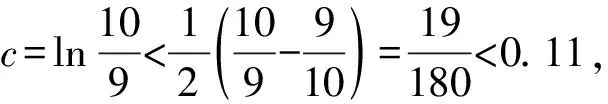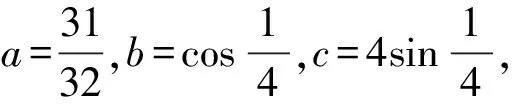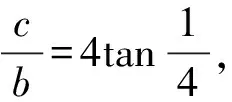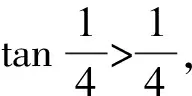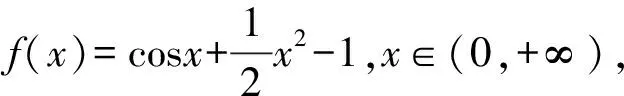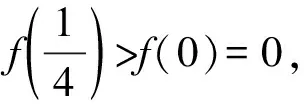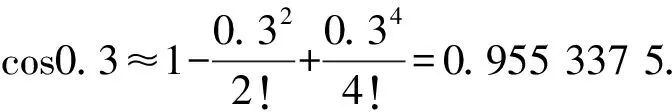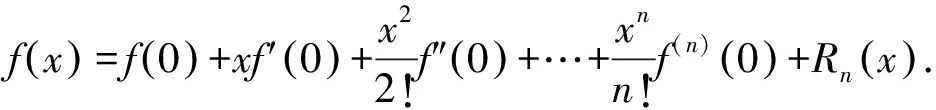數學試題中的隱數學文化
——以2022年數學新高考Ⅰ卷第7題為例

來 偉 王 莉

(1.安徽省蚌埠第二中學; 2.安徽省滁州市第二中學)

新高考進入了無綱時代,2022年的數學試題,突出了試題的創新性,優化了試卷的結構,變換了提問的方式,改變了試題結構,增加了試題的新穎性和靈活性,促使學生運用知識解決新問題的能力.返溯2020年,2021年,2022年以及新高考八省適應性訓練的一致性和差異性,規律性可能是未來高考的命題趨勢,差異性是高考釋放的信息,這要求我們更新觀念,查缺補漏,新高考倒逼教學改革.

近幾年的高考數學中,關于以導數為背景的比較大小的題目,出現頻率較高,試題著重考查了學生構造函數,運用不等式,對課本擴展的知識和二級結論掌握程度的綜合體現.這些題目往往有著高等數學的背景,使壓軸題更具新意,增加了試題的難度和區分度,本文通過2022年高考試題的例題分析,借鑒高等數學的知識,開闊學生的數學思維寬度,以期提高數學思維力.

下面我們以2022年新高考數學Ⅰ卷第7題為例:

( )

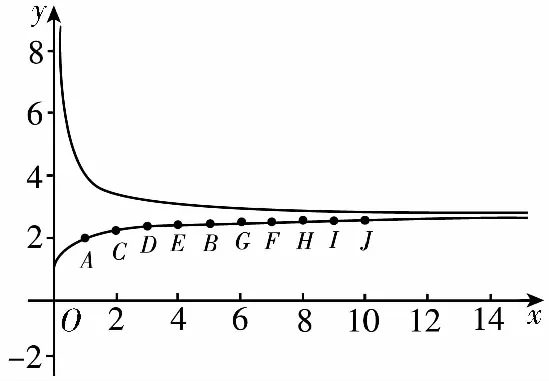
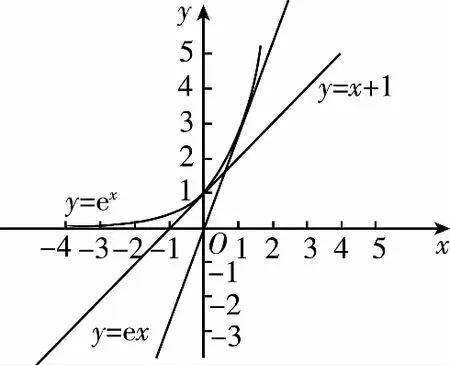
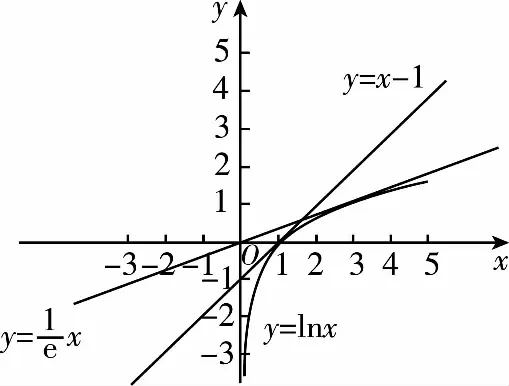
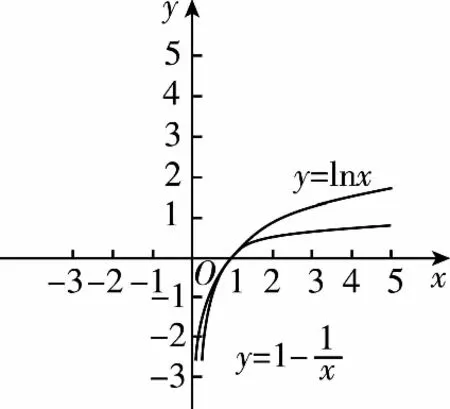
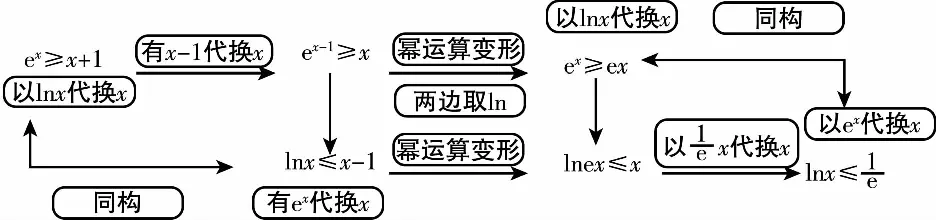
A.a

C.c

方法一:構造函數

設函數f(x)=ln(1+x)-x(x>-1),

當x∈(-1,0)時,f′(x)>0,

當x∈(0,+∞)時f′(x)<0,

所以f(x)=ln(1+x)-x在(0,+∞)上單調遞減,在(-1,0)上單調遞增,

設g(x)=xex+ln(1-x)(0

令h(x)=ex(x2-1)+1,h′(x)=ex(x2+2x-1),

h′(x)<0,h(x)=ex(x2-1)+1單調遞減,

h′(x)>0,h(x)=ex(x2-1)+1單調遞增,

又h(0)=0,

函數g(x)=xex+ln(1-x)單調遞增,

所以g(0.1)>g(0)=0,即0.1e0.1>-ln0.9,

所以a>c,故選C.

方法二:運用三個重要的不等式:

lnx≤x-1(當且僅當x=1時,等號成立)

ex≥x+1(當且僅當x=0時,等號成立)

①“切線”不等式的圖形直觀

ex≥x+1 ex≥ex

②“切線”不等式變形轉換

∴a

又∵a=0.1e0.1>0.1×(1+0.1)=0.11,

∴c

方法三:利用函數的凹凸性

設f(x)在區間I上有定義.

(1)若對任意的x1,x2∈I且x1≠x2,有

則稱f(x)在(a,b)內為凸函數,如圖1所示.

圖1

(2)若對任意的x1,x2∈I且x1≠x2,

則稱f(x)在(a,b)內為凹函數,如圖2所示.

圖2

∵函數y=lnx是(0,+∞)上的凸函數,

則b>a.

又∵a=0.1e0.1>0.1×(1+0.1)=0.11,

∴c

試題背景:隱數學文化,高等數學重要極限:

比較a與b即0.1e0.1與19即e110與109即110與ln109即1與ln(1+19)10即e與(1+19)1+9比較b與c即19與ln109即1與9ln109即1與ln(1+19)9即e與(1+19)9

本道試題隱含高等數學中函數的凹凸性和重要極限的背景,突出了高中數學知識和大學數學的潛在的聯系,以較高的視角,對高考試題進行分析和思考.

( )

A.c>b>aB.b>a>c

C.a>b>cD.a>c>b

f′(x)=-sinx+x>0,

設g(x)=-sinx+x,則g′(x)=-cosx+1≥0,

所以f′(x)在(0,+∞)上是增函數,

所以f′(x)>f′(0)=0,

所以f(x)在(0,+∞)上單調遞增,

所以b>a,所以c>b>a,故選A.

【解法二】回歸教材:人教A版必修一P256第26題

英國數學家泰勒發現了如下公式:

其中n!=1×2×3×4×…×n.

∴b>a.

∴c>a.

追本溯源:高等數學泰勒公式(曲線逼近,近似計算)

本道試題隱含高等數學中泰勒公式,以課本知識為本源,寬角度,多觀點地考查學生的基本素養,有層次的了解學生的理性思維和進一步深造的潛能.