多向探究解法 落實核心素養

福建省武夷山市第二中學

林夢雨

1 試題呈現

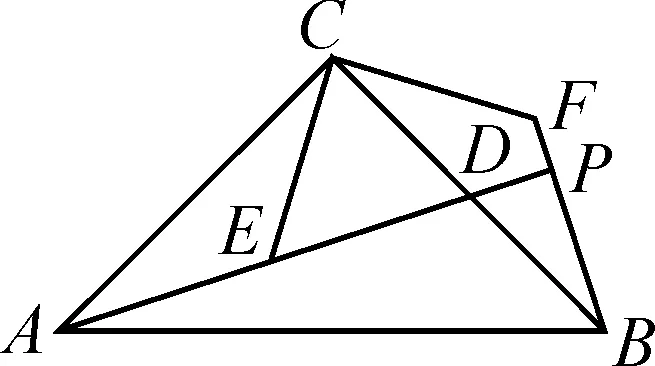
圖1

(2022湖北黃岡中考模擬)

問題背景：如圖1，在△ABC中，∠ACB=90°，AC=BC，AD是BC邊上的中線，E是AD上一點，將△CAE繞點C逆時針旋轉90°得到△CBF，AD的延長線交邊BF于點P.

問題探究：(1)探究EP，FP之和與BP之間的數量關系.

①先將問題特殊化，如圖2，當CE⊥AD時，直接寫出EP，FP之和與BP之間的數量關系；

②再探究一般情形，如圖1，當CE不垂直AD時，證明①中的結論仍然成立.

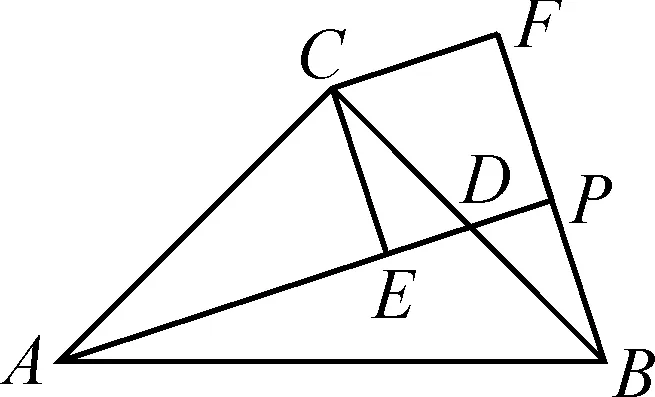
圖2

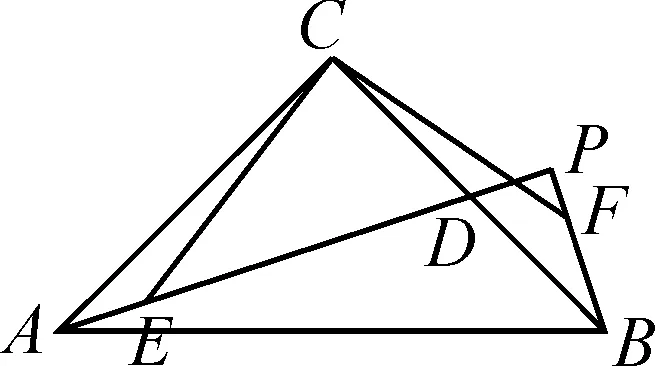
圖3

拓展探究：(2)如圖3，若AD的延長線交BF的延長線于點P時，直接寫出一個等式，表示EP，FP，BP之間的數量關系.

2 考點及特征分析

本題是一道幾何探究問題，以旋轉為知識載體，探求幾何圖形在特殊情況和一般情況下的性質，問題由易到難，逐層深入.思考模式為：利用上一個問題的解決方法來類比解決下一個問題.如果不能解決，就把兩個問題結合起來分析，找出不能類比的原因和“不變”特征，圍繞“不變”特征進行新的探索.本題第①問易上手，利用旋轉的性質，以及正方形、全等三角形等知識點就可以解決；第②問類比第①問的處理方式構造正方形，經過兩次全等即可解決. 第(2)問，同樣是在同一位置構造正方形，證兩次全等，只不過過程與前兩問不完全一致而已，結論由“線段之和”改成了“線段之差”，但解題所用的方法、知識基本相同. 此類題目體現“特殊與一般”，運用類比思想探究科學解決問題的基本思路，是促進學生深度學習，培養學生理性思維的較好素材.

3 試題解析

經過探究與思考，發現本題解法較多，簽于篇幅有限，筆者重點分析最具研究價值的第(2)問，現整理如下.

解法1：設元思想.

圖4

點評：解法1思路簡單、清晰.由旋轉得對應角相等和對頂角相等，直接得到相似三角形對應邊成比例.由直角三角形聯想到勾股定理，在線段相等的轉換處理中，運用了設而不求的方程思想，轉換非常巧妙，大道至簡.

解法2:作垂證正方形.

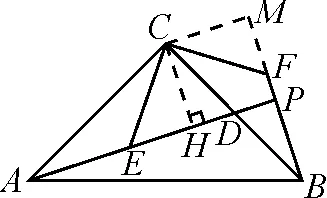
圖5

如圖5，過點C作CH⊥AP交于點H，過點C作CM∥AP交BF的延長線于點M，則四邊形CHPM為矩形.證△CEH≌△CFM，得到四邊形CHPM為正方形.再證△CHD≌△BPD,得CH=BP.故EP+FP=EH+PH+FP=FM+BP+FP=2BP.

點評：解法2延續了第①問的解題思路，類比特殊情況構造正方形解題.滿分的學生大部分都是用這種方法，亦屬本題的自然解法.

解法3:截長法，移花接木.

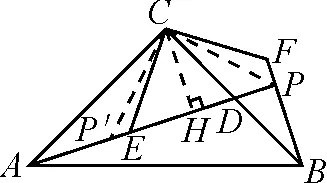
圖6

如圖6，在AE上截取一點P′，使得EP′=PF，過點C作CH⊥AP交于點H.易證△CEP′ ≌△CFP，得CP′=CP，∠P′CP=90°，則BP=CH=PH=P′H.

故EP+FP=EP+EP′=PP′=2CH=2BP.

解法4:補短法.

圖7

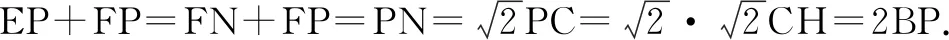
點評：解法3和解法4思路來源于證明線段之間的和差關系，聯想到截長補短法. 截長補短法也是初中階段最為常見、最為經典的解決線段和差問題的策略.

解法5:“K字型”全等.

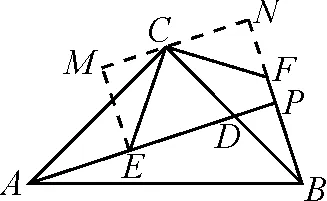
圖8

如圖8，過點C作MN∥AP，分別過點E，F作MN的垂線，垂足為點M，N.易證四邊形EMNP是矩形，得EP=MN，DP∥CN.又由D為BC中點，可知點P為BN中點.易證△ECM≌△CFN，得CM=FN，CN=EM.則EP=MN=MC+NC=FN+PN=BP-FP+BP，即EP+FP=2BP.

點評：由等腰直角三角形聯想到構造一線三垂直“K字型”全等，由中點和平行得到中位線，從而將線段之間的關系進行轉換.

解法6:四點共圓.

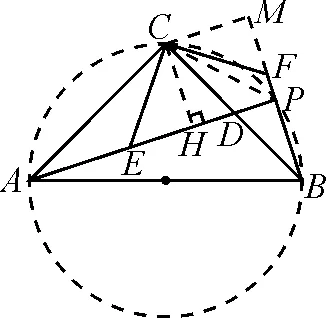
圖9

如圖9，過點C作CH⊥AP交于點H，CM⊥BF交BF的延長線于點M.由∠ACB=∠APB=90°，得點A，C，P，B四點共圓，則∠CBA=∠CPD=∠CPF=45°.由角平分線性質，得CH=CM，從而得到四邊形CHPM為正方形.故EP+FP=EH+PH+FP=FM+BP+FP=2BP.

點評：由共斜邊且在同側的兩直角三角形聯想到四點共圓，再運用圓周角定理的推論和圓內接四邊形的性質得到CP為∠FPA的角平分線.此法看似簡單，但對四點共圓及圓的性質要掌握得非常熟練，富有創新性，有鮮明特點，值得點贊.

4 解題反思

4.1 了解類比綜合題特點

近幾年，類比拓展探究問題越來越頻繁出現在各類考試中.因為它既能很好地考查《義務教育數學課程標準》中對學生知識要求的掌握情況，也能更好地考查學生活學活用的能力，即能否把書本知識很好地遷移、拓展到新的問題情境之中. 這樣的題型一般多以大題出現，涉及知識點較多，與圖形變換知識有關，對學生運用知識的能力要求較高.

正如美國數學家G.波利亞所言：“類比是一個偉大的引路人.”類比探究問題的解決策略，將一般條件與特殊條件相結合，由特殊情形過渡到一般情形；或由簡單到復雜，逐步深化；解決問題的思想方法一脈相承.體現了“條件類似，圖形結構類似，解法類似”的特點.

解決類比探究問題的方法是類比.如，類比輔助線，類比思路，將特殊情形中的問題解決方法類比到一般情形中去.對比前后條件的變化，尋找并利用不變特征，類比方法，類比圖形特征，進行推理求證. 正如德國天文學家、數學家開普勒曾指出：“我重視類比勝過任何別的東西，他是我最依賴的老師，在幾何學中它應該不容忽視.” 因此，培養學生解決類比問題的解題策略、解題信心、解題心理及解題方向至關重要.

4.2 一題多解，培養創新素養

創新素養是初中生的核心素養，是現代數學教學的基本任務，獨立思考、理性思考是創新的核心與關鍵.面對問題，認真審題是解題的基礎.可以由已知向結論推理，或由結論向已知推證；或者從兩邊向中間追尋，尋找已知與結論之間的橋梁，由題目的已知條件能夠挖掘出什么重要結論，由條件能聯想到什么，由結果還能聯想到什么.

一題多解是目前一般學校數學教學研究的方向，在課堂中一般都有體現.它是一種過程性變化變式教學，在實際應用教學中，也特別關注學生數學能力的有效提升.特別強調教師要結合數學問題，將條件與結論不斷進行轉換，凸顯自身對不同教學模擬內容、方法的不同理解.這有利于學生知識方法的鞏固，數學思想的發展，創新意識的提升.

總之，在平時教學中，教師要了解學生知識與能力的起點，明晰學生的困難與需要，不能浮光掠影，而應深度揭示題目的內涵，挖掘思想品質，提升思維品質.