基于SVMD和SDRSE方法的輸電線路局部放電信號診斷分析

李 寧，梁河雷，程 旭，李 峰

（1.國網河北省電力有限公司 衡水供電分公司，河北 衡水 053000； 2.河北科技大學 電氣工程學院，河北 石家莊 050091）

輸電線路已成為未來能源轉型的關鍵傳輸工具，在能源升級優化過程中，發揮了重要作用。但隨著交聯聚乙烯（cross-linked poly-ethyline，XLPE）輸電線路超過一定的使用期限后，會因保護層老化破壞等問題而無法獲得良好的絕緣性能［1-2］，進而引起嚴重的經濟損失。因此，要求對輸電線路開展絕緣檢測，保證輸電線路的穩定運行。在輸電線路絕緣檢測方面，局部放電（partial discharge，PD）法屬于一項得到廣泛應用的技術，可滿足不同類型輸電線路的監測需求［3-4］。

近年來，已有較多學者針對PD噪聲去除的過程展開研究，包括奇異值分解、自適應濾波、小波轉換、經驗模態分解等多種方式［5-9］。隨著人們對噪聲去除過程研究的持續深入，逐漸形成集合經驗模態分解（ensemble empirical mode decomposition，EEMD）、完全集合經驗模態（complete ensemble empirical mode decomposition，CEEMD）、經驗模態分解（empirical mode decomposition，EMD）優化算法等多種噪聲處理技術［10-11］。雖然采用上述算法可實現一定的噪聲去除效果，但無法克服EMD算法本身的缺陷，尤其不能完全消除模態混疊的缺陷。變分模態分解（variational mode decomposition，VMD）是利用傳統維納濾波方式實現的信號處理算法［12］，可實現優異的噪聲魯棒性，一方面增強小波分解自適應能力，另一方面可消除EMD算法所面臨的模態混疊問題，對處理非線性信號具有重要作用。懲罰因子α和分解層數K均會顯著影響VMD 算法分解性能［13］。前期大部分文獻都是根據經驗方法設置α和K，降低了分解效率，易造成欠分解及過分解的問題。

此外，熵作為判斷時間序列復雜性的方法，也在對非線性信號平穩性分析方面發揮了重要作用，包括排列熵、近似熵等［14］。但根據近似熵進行計算時，受數據長度的直接影響，采用排列熵進行計算時未針對信號幅值開展分析。根據上述研究結果，本文開發了一種通過Spearman變分模態分解（spearman variational mode decomposition，SVMD）和空間相關遞歸樣本熵（spatial dependence recurrence sample entropy，SDRSE）來去除局部放電信號噪聲的技術，采用該方法去噪，可效抑制PD信號噪聲，獲得更優的去噪指標。

1 基本理論

1.1 空間相關遞歸樣本熵

以SDRSE 進行計算時能夠獲得信號序列參數，有助于準確區分本征模態分量（intrinsic mode function，IMF）類型。求解時按照以下條件建立序列集合X｛x1，x2，x3，…，xN｝，通過坐標延遲的方式確定重構相空間，得到表達式如下：

式中：Xi為重構相空間包含的向量；i=1，2，…，N-（m-1）；m為嵌入維數；τ為延遲時間。

為相空間建立遞歸矩陣表達式如下：

式中：d（Xi，Xj）為Xi與Xj的切比雪夫距離；Ri，j為遞歸函數；ε為Heaviside函數。

從重構空間內隨機選擇2個向量代入以上計算式中構建矩陣，以黑點代表（i，j）坐標的Ri，j=1參數，可得到時間序列通過相空間重構形成的遞歸函數。

通過灰度共生矩陣建立二值共生矩陣（binary level co-occurrence matrix，BLCM），得到式（3）的函數形式：

式中：B為遞歸函數；I（x，y）為x、y坐標位置上的像素點；p和q為0 或1 的二進制取值；N為總遞歸數。

本研究設計得到2×2 大小的BLCM 矩陣，BLCM（1，1）代表黑色像素（0，0）個數，BLCM（2，2）代表白色像素（1，1）個數。

1.2 改進小波閾值去噪

處理噪聲主導分量時，選項小波閾值去噪形式。進行小波轉換的具體思路為：先對含噪信號實施小波轉換獲得小波系數，再設置合理閾值，對各層小波系數實施篩選轉換，最后重構計算經過處理的小波系數。本文構建的新型小波閾值去噪函數如下：

式中：ωi，j為小波系數；λ為小波閾值

本文設計的算法流程如圖1所示。

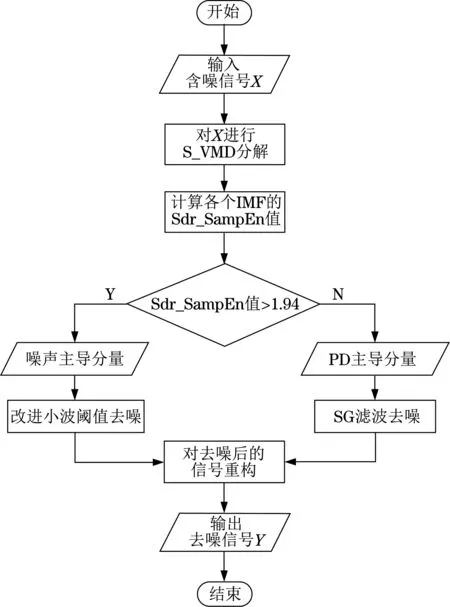
圖1 本文去噪方法流程Fig.1 Flow chart of denoising method in this paper

2 仿真信號分析

2.1 PD信號仿真模型

本文采用數振蕩衰減函數開展模擬測試，表達式如下：

式中：S為衰減函數；A為幅值；fc為振蕩頻率。

控制采樣頻率50 MSa/s，持續采樣40 μs，形成純凈PD 信號，如圖2（a）所示。設置信噪比等于-1 dB 的高斯白噪聲和周期窄帶信號，測試中通過不同頻率與幅值正弦信號形成周期窄帶信號。經噪聲疊加獲得的波形如圖2（b）所示，窄帶干擾參數設置見表1，初始PD 信號已在噪聲信號中呈現淹沒狀態，不能對其進行準確分辨。

表1 窄帶干擾參數設置Tab.1 Setting of narrowband interference parameters

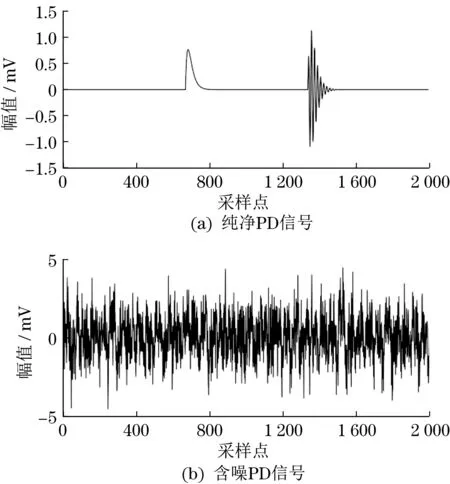
圖2 仿真PD信號Fig. 2 Simulation of PD signal

2.2 仿PD信號去噪

先對含噪聲的PD 信號開展SVMD 分解，形成IMF分量，如圖3所示，得到SDRSE參數，見表2。

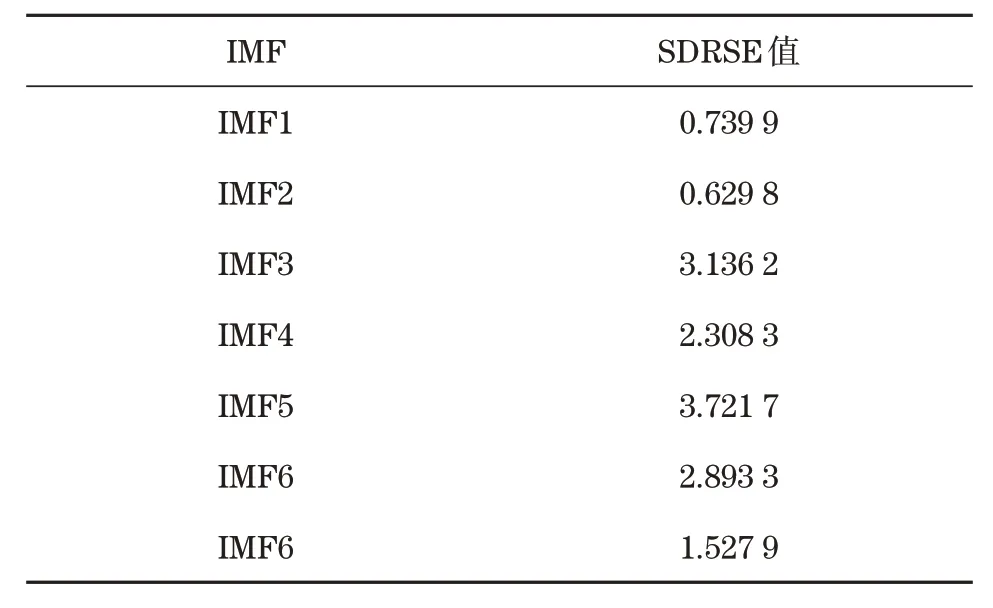
表2 IMF的SDRSE值Tab.2 SDRSE values of IMF

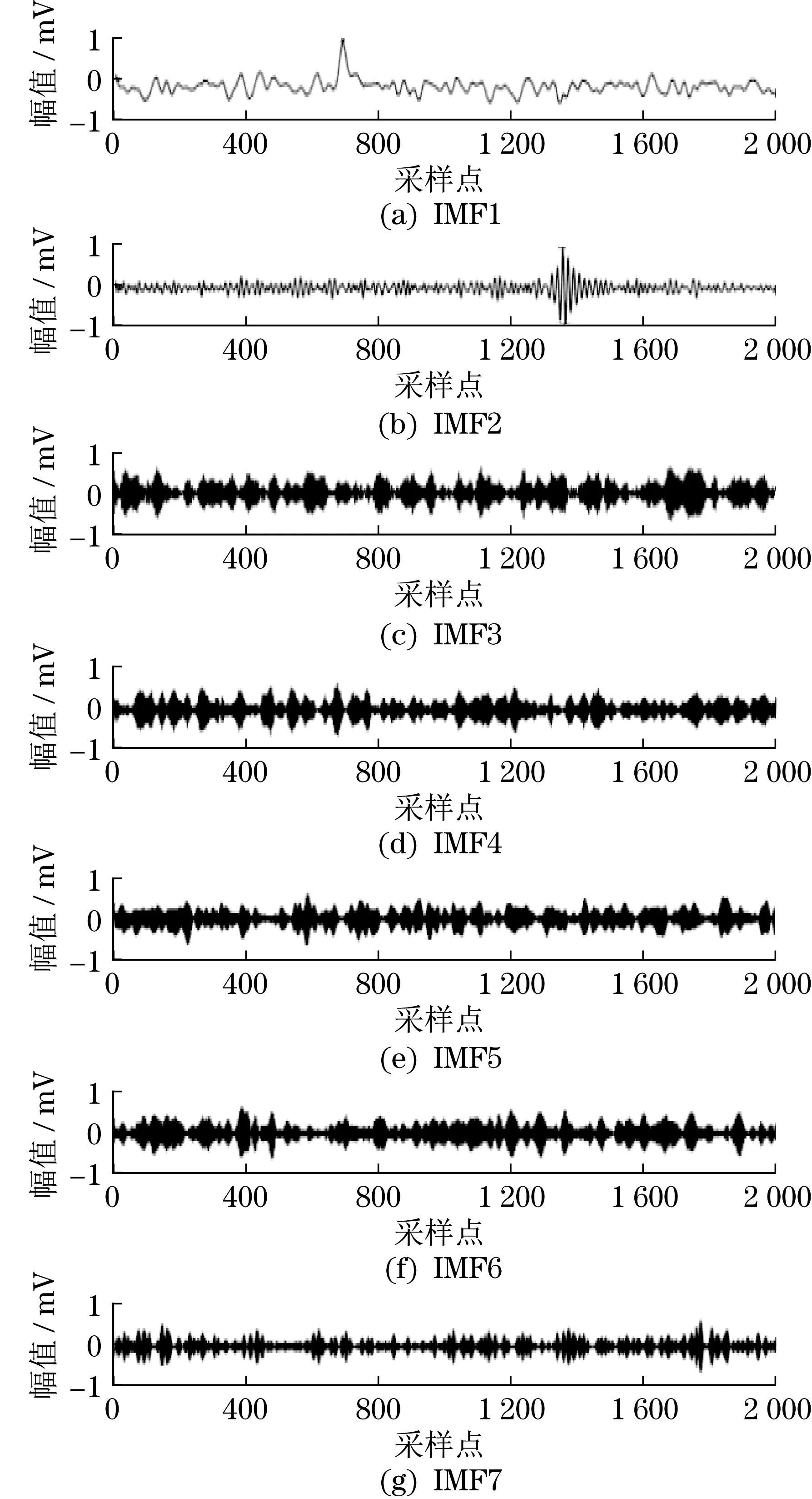
圖3 SVMD 分解Fig.3 SVMD decomposition

由表2可知，IMF1、IMF2和IMF7均未超過1.93的SDRSE指標，可將其作為PD主導分量。IMF7對應的SDRSE值與IMF1和IMF2之間存在明顯差距，表明IMF1和IMF2含有更高比例的PD參數，包含PD主導分量的特征也大幅超過IMF7。其他IMF 的SDRSE均超過1.93，可將其作為噪聲主導分量。以線性平滑濾波方法計算PD主導分量，再利用改進小波閾值完成噪聲主導分量的降噪分析，之后重構獲得去噪處理的PD信號。最后，依次選擇自適應變分模態分解（adaptive variational mode decomposition，AVMD）［3］、CEEMD-EEMD和S-SVD 3種算法與本文提出的算法開展去噪測試，對比結果如圖4所示。

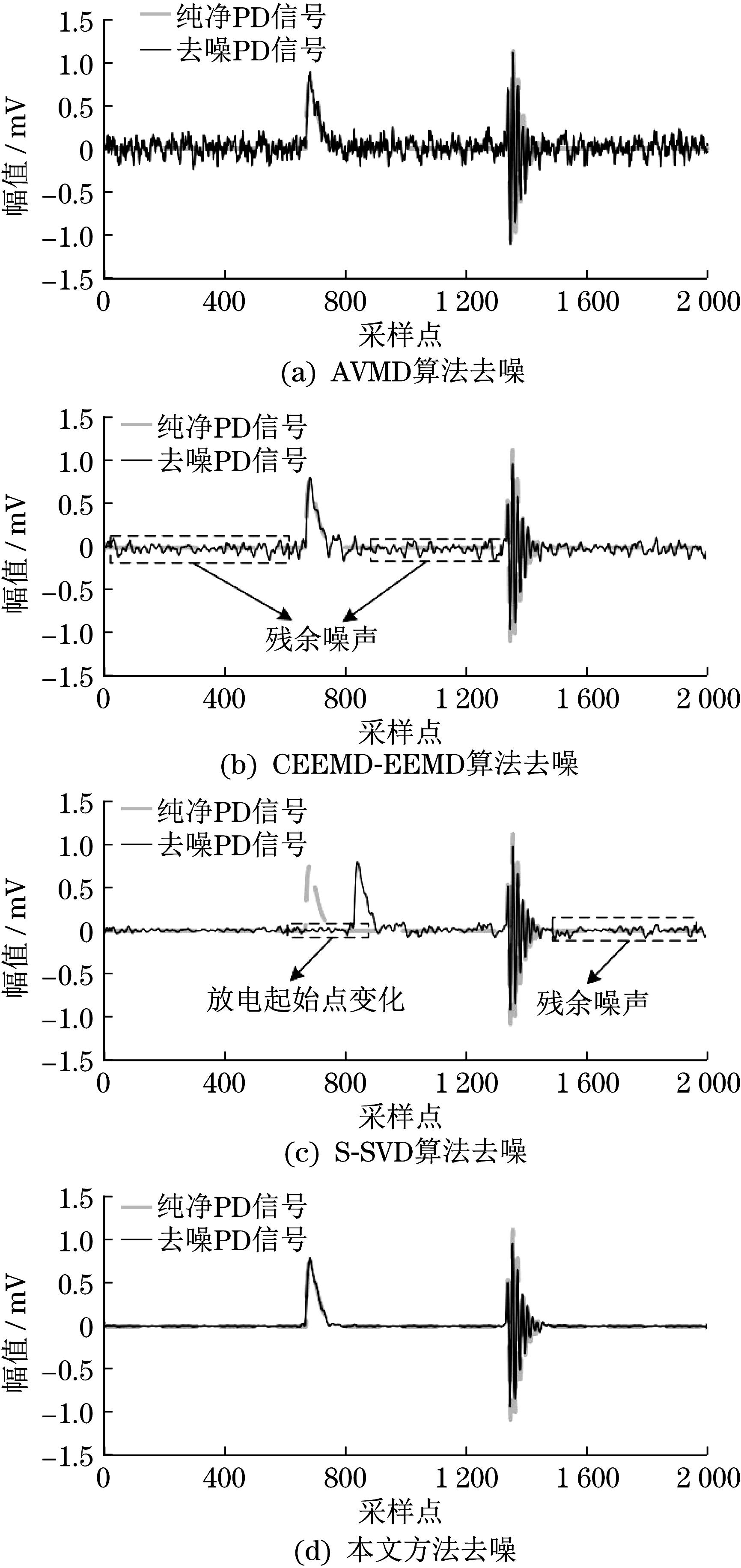
圖4 仿真PD信號去噪結果Fig.4 Denoising result of simulated PD signal

由圖4（a）可知，對含噪PD 信號完成AVMD 處理后，依然有大量的白噪聲，未達到良好的去噪效果；由圖4（b）可知，雖然利用CEEMD-EEMD 算法優化模態混疊效果，但無法完全去除；由圖4（c）可知，以S-SVD 去噪時，出現第1 個PD 放電起始點偏移問題，無法滿足精確定位與模式識別要求；由圖4（d）可知，以本文方法去噪時，形成了與初始PD信號相同的效果，可實現優異的抗高斯白噪聲，并避免周期窄帶產生的干擾。

為分析采用本文方法對各程度白噪聲進行去噪的性能，為圖2（a）的純凈PD 信號設置不同白噪聲，控制信噪比依次達到-3、0 和3 dB，再加入同樣程度窄帶干擾信號，通過前期設置的指標綜合評價各類去噪方法，測試結果見表3。表3 中，評價指標為信噪化（sign noise ratio，SNR）、歸一化相關系數（normalized correlation cofficient，NCC）、均方根誤差（root mean square error，RMSE）。結果顯示，采用本文設計的方法對同樣條件進行去噪評價時，可以獲得比其他3 種算法更優的性能。同時考慮到本文方法的組成結構復雜，進行仿真期間需調用大量函數，導致算法運算時間明顯增加，通常要占用5 s以上的仿真時間，因此還需優化SDRSE 計算過程，進而獲得更優的時效性。

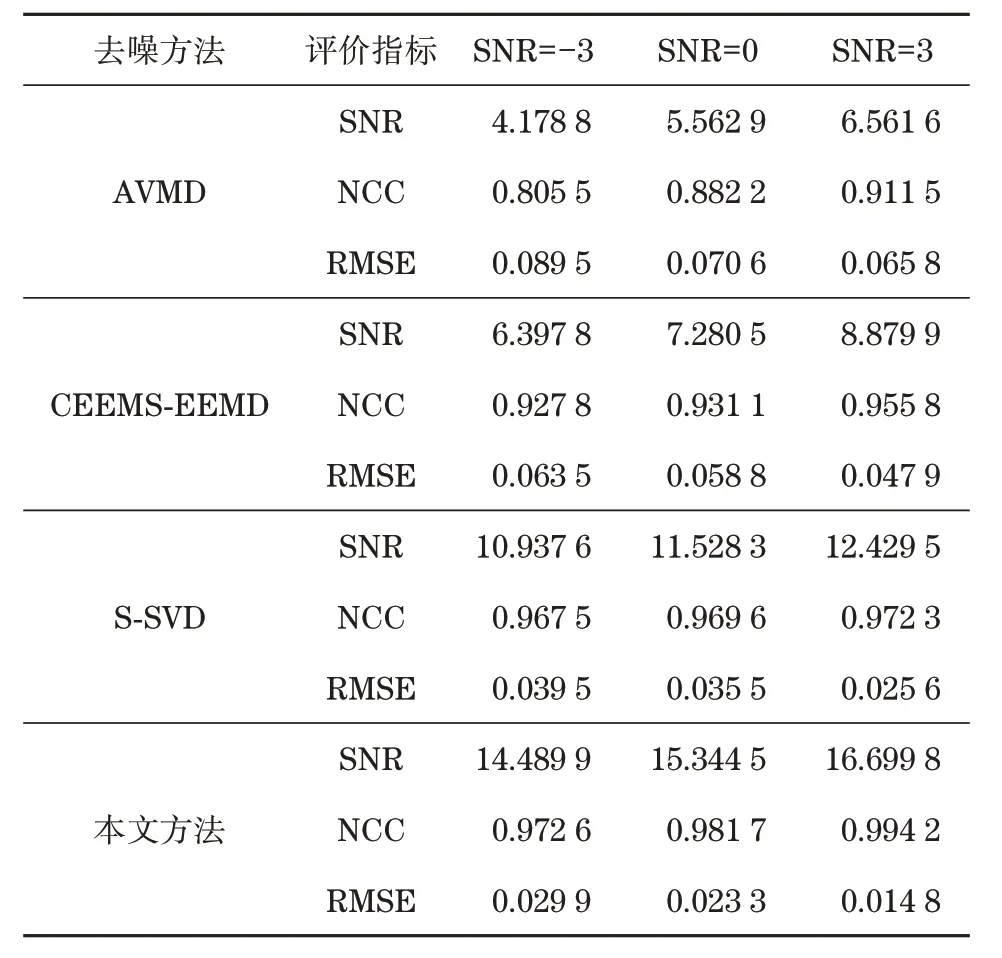
表3 仿真PD信號去噪效果對比Tab.3 Comparison of denoising effect of simulated PD signal

3 實測信號分析

為驗證本文去噪的有效性，在實驗室條件下建立局部放電系統，并對10 kV 輸電線路開展PD 信號測試，如圖5 所示。將50 MHz 高頻電流傳感器（high frequency current transducer，HFCT）安裝于輸電線路接地線處，再運用示波器與計算機顯示放電脈沖曲線，結果如圖6所示。

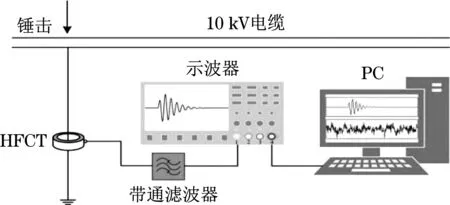
圖5 局部放電測試平臺Fig.5 Partial discharge test platform

圖6 實測PD信號Fig.6 Measured PD signal

通過實驗測試得到的PD信號易形成較高的信噪比，因此針對初始PD信號，采用人為方式加入窄帶干擾信號，其幅值和頻率依次介于0.5~1.5 mV與0.8~2.0 MHz 之間，進而獲得疊加窄帶干擾的含噪信號，結果如圖7所示。

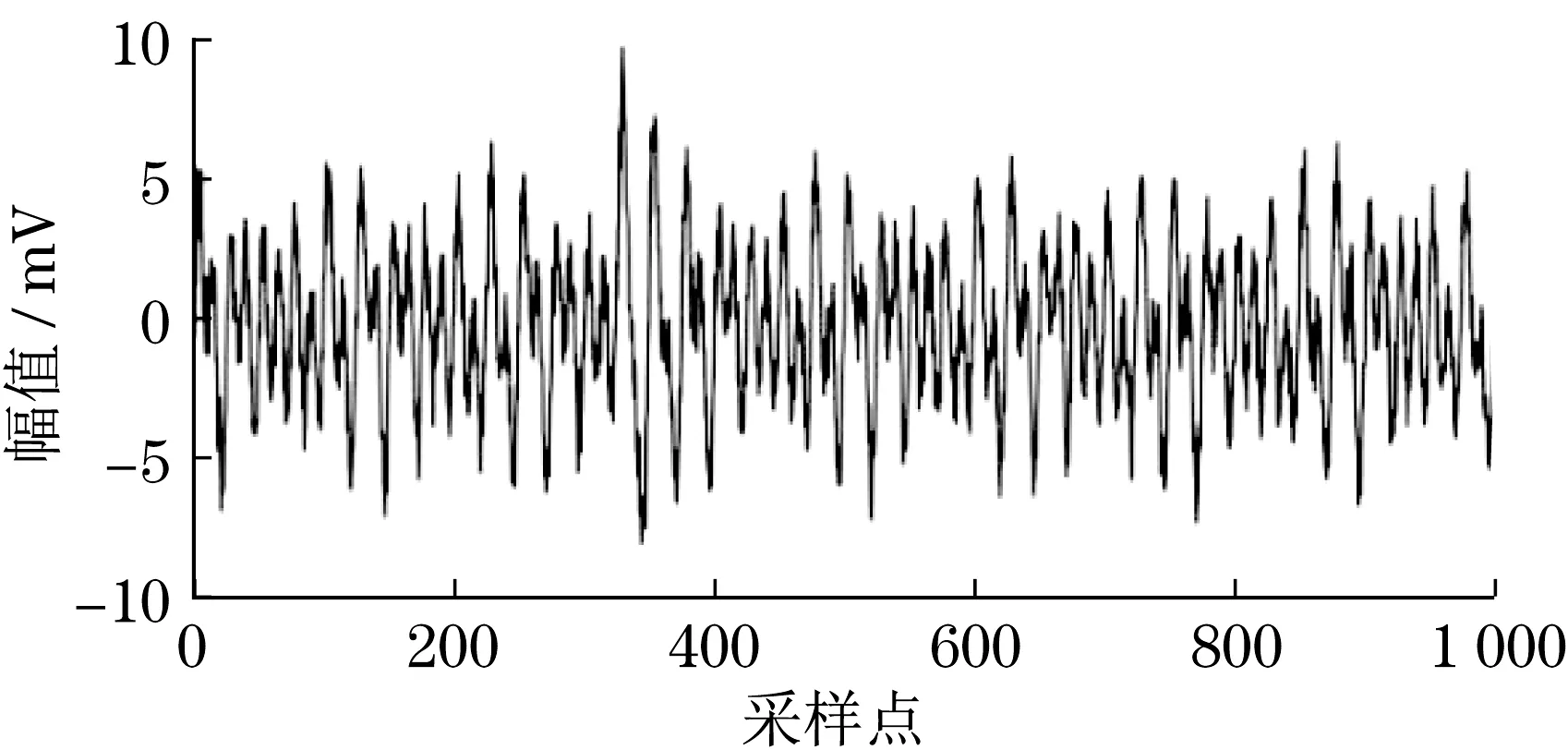
圖7 疊加窄帶干擾的PD信號Fig.7 PD signal superimposed with narrowband interference

由圖7 可知，此時初始PD 信號已被淹沒在噪聲中，不能對其進行準確辨識。同時形成與圖6（b）相近的含噪PD 信號，此時可選擇同樣的閾值p。對比本文算法和其他3 種去噪方法對PD 信號去噪的性能，結果如圖8所示。

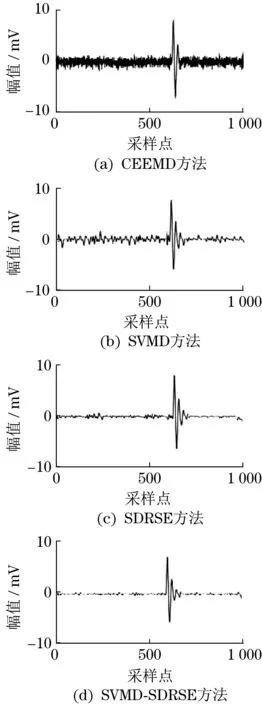
圖8 實測 PD 信號去噪結果Fig.8 Denoising results of measured PD signals

由圖8 可知，以AVMD 算法處理得到的波形中存在大量底噪信號，由于CEEMD-EEMD 算法不能有效去除白噪聲和周期窄帶干擾影響，對PD 信號辨識性能造成不利影響，采用本文去噪方式可顯著抑制最終的信號噪聲。以不同去噪方法得到的降噪額定值（noise reduction rating，NRR）見表4。其中，使用本文去噪方法可獲得最大NRR，對實測信號的去噪性能最優。

表4 實測PD信號去噪效果對比Tab.4 Comparison of denoising effect of measured PD signal

4 結論

（1） 仿真信號分析結果表明：以本文方法去噪時，形成與初始PD信號相同的效果，可實現優異的抗高斯白噪聲并避免周期窄帶產生的干擾，獲得更優的性能。

（2） 實測信號分析結果表明：對比本文算法和其他3 種去噪方法對PD 信號去噪的性能，采用本文去噪方式，可顯著抑制最終的信號噪聲，獲得最大NRR，對實測信號的去噪性能最優。