2022年廣州中考數學卷第25題的解法探究及啟示
覃啟藝
(廣州市白云區華新學校,廣東 廣州 510440)
1 考題呈現
(2022 年廣州市中考數學第 25 題) 如圖1,在菱形ABCD中,∠BAD=120°時,AB=6,連接BD.
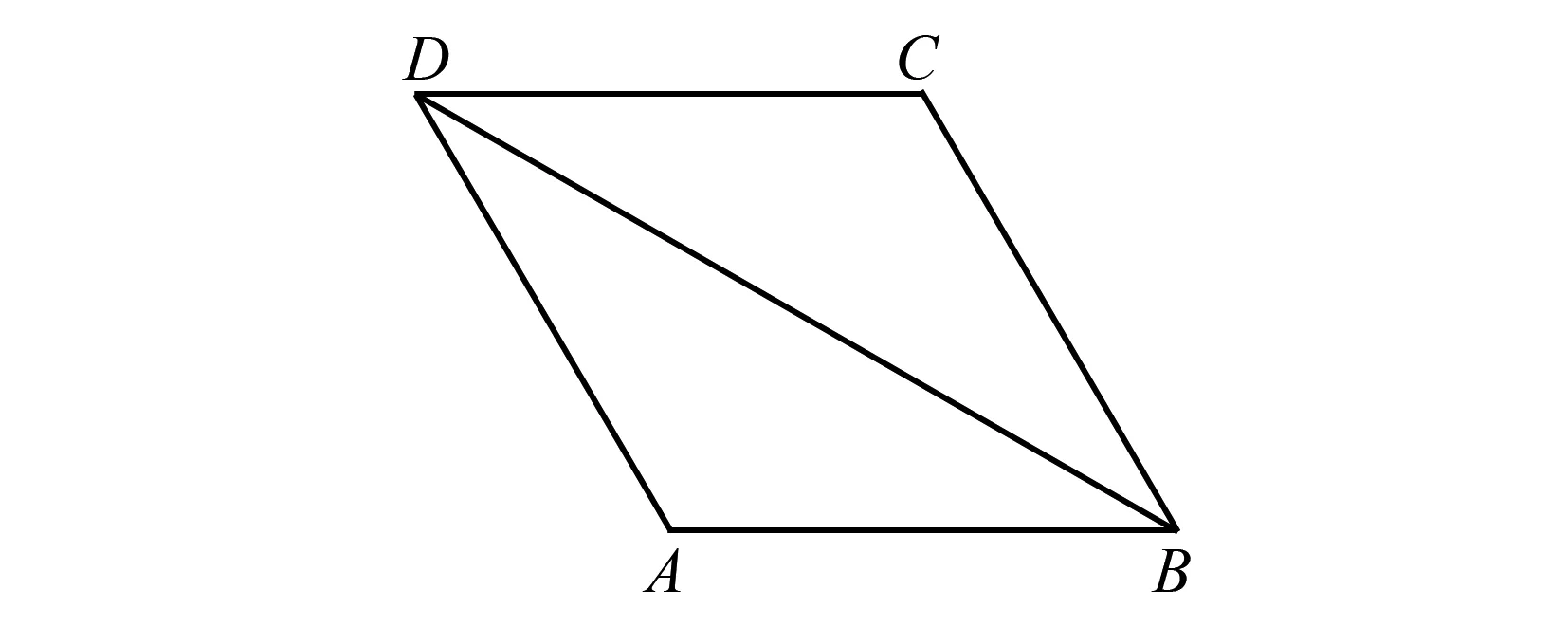
圖1 2022年廣州市中考數學第25題圖
(1)求BD的長;
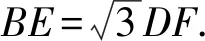
①當CE⊥AB時,求四邊形ABEF的面積.

2 思路歷程
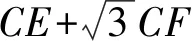
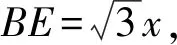
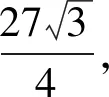

3 方法探究

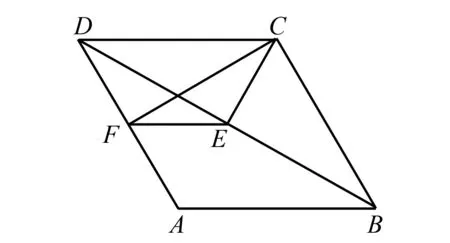
圖2 思路1解析圖

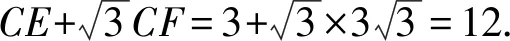
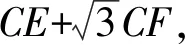
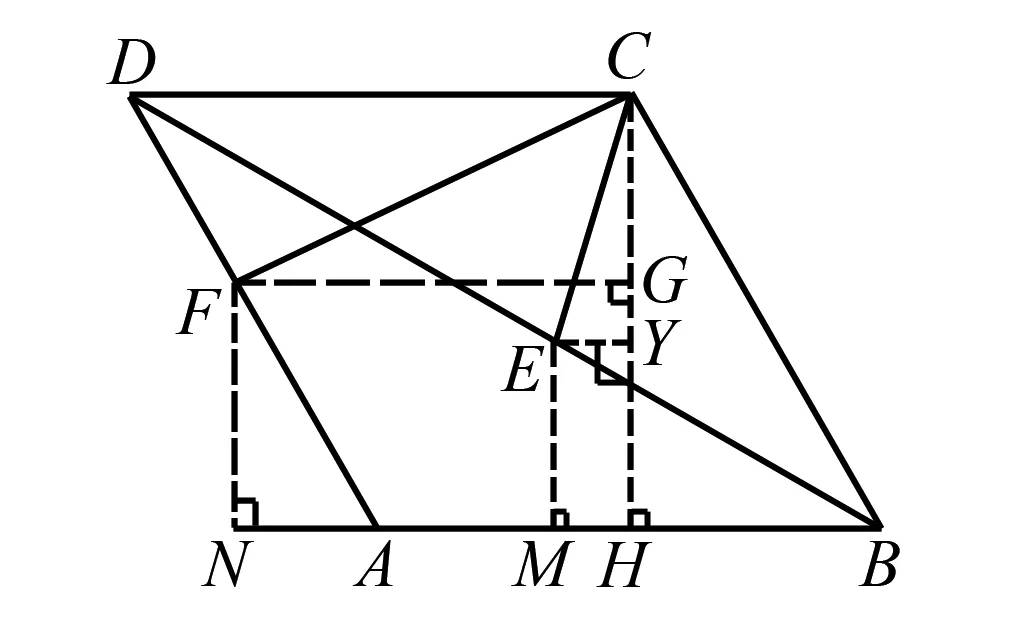
圖3 思路2例題圖
如圖3,分別過點C、E、F作BA或其延長線的垂線,垂足分別為H、M、N,再過點F、E分別做CH的垂線,垂足為G、Y,則四邊形FNHG為矩形.
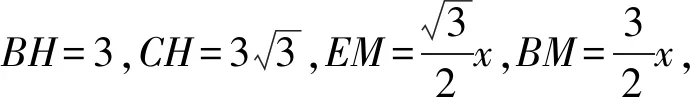
代入計算得:
≥3+9=12


以BD為邊作等邊△DBP(如圖4),在DB上找點G,使DG=BE,連接GP,CG,易得CG=CE.
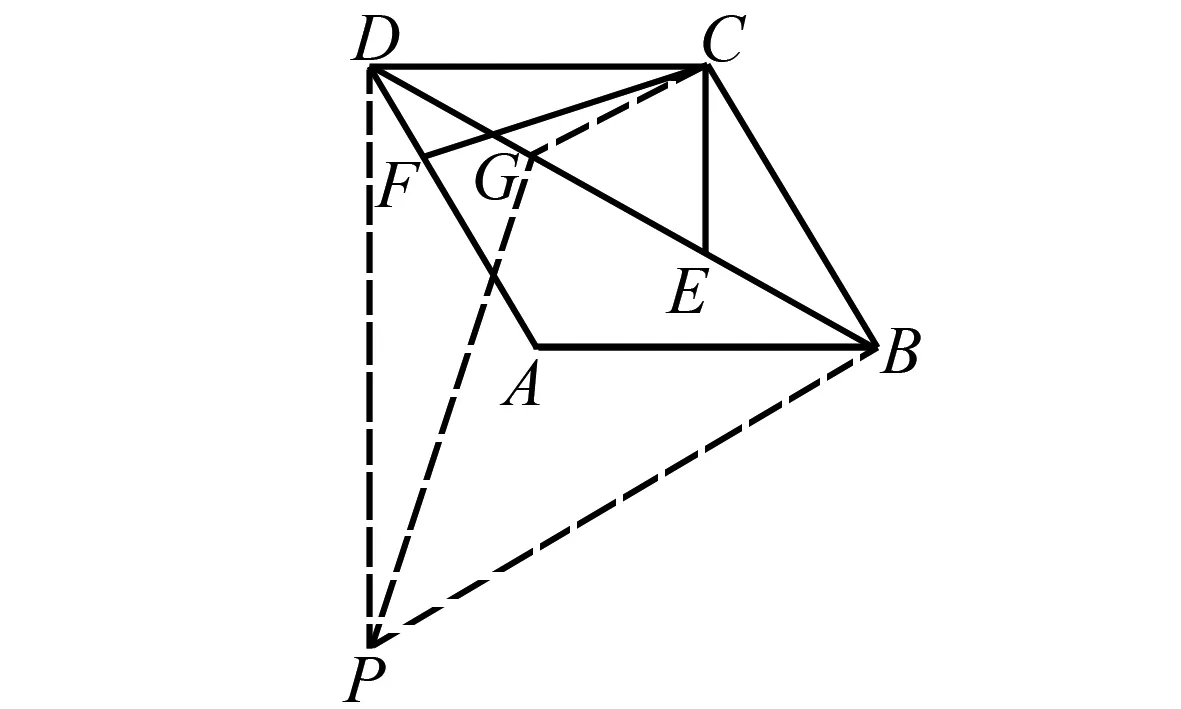
圖4 思路3解析題圖
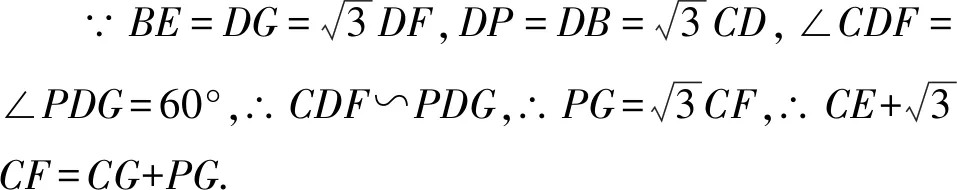


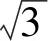
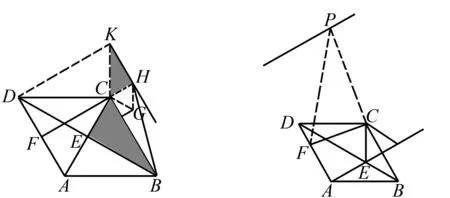
圖5 思路2解析題圖 圖6 思路2擴展圖
∴K為定點,∠HCK=∠ECB為定角,∴點H的軌跡為線段.
連接DK,易證∠CKD=60°,∠CDK=30°,DK⊥DA,且DK⊥KH,
∴KH∥AD.
∴當F、C、H共線且CF⊥AD時,CH+CF最小.下面只需求出CH+CF的最小值即可.
思路4利用余弦定理
在△CDF和△CBE中分別用余弦定理得:
CF2=DF2+CD2-2CD·DFcos60°=x2+36-6x=(x-3)2+27,
CE2=BE2+BC2-2BE·BCcos30°=3x2+36-18x=3(x-3)2+9,
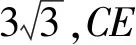
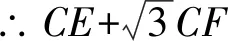
4 考點分析
本題可能涉及到的考點主要有:
幾何動態:點E的運動變化,導致點F的變化,而相應的CE和CF的長度也發生變化.找準它們的變化規律是解決問題的關鍵.
幾何最值:從形式上看,似乎是屬于“胡不歸模型”或者“阿氏圓模型”,如果套用這兩個模型,就會誤入雷區.它其實是一個拼接模型,拼接后應用“兩點之間,線段最短”或者“垂線段最短”.
幾何變換:在構造的過程中,對稱變換、旋轉變換是初中數學常考的考點,但利用相似變換去構造更加凸顯解答此題的靈活性.作為部分數學較好的精英學生,研究此種變換恰好可以彌補我們學習數學的一個空缺.
三角函數:三角函數是解決三角幾何問題的常用方法.特別是在特殊的直角三角形中,記住常用的特殊三角函數值,活用三角函數的知識,在解三角幾何問題時有特殊的作用.
5 感悟與啟示
中考要求學生掌握各方面的能力.從 2022 年廣州中考數學 25 題中我們可以看出,廣州中考非常重視對學生抽象能力、空間想象能力、運算能力和邏輯思維能力等數學核心素養的考查.
平時教學要重基礎.基礎知識是學生分數的生命線,我們一定要教育學生牢牢地打好基礎,避免在簡單的問題中出錯.
考前復習要提能力.我們不難發現,大多學生在處理簡單的幾何題、運算題時毫無壓力,而面對一些較難的綜合題時便顯得力不從心.問題在哪?他們經常是對簡單的問題反復練習,而在難題上,經常是退卻和自我否定的.因此,我們要告誡學生,提升自己綜合能力的關鍵就是要認真細心、持之以恒地把難題做好做對,并在此基礎上多吸收、多歸納、多反思.
學有余力要提前學.華南師范大學教授吳康老師提到:“高中的知識如余弦定理等在中考中可以直接使用.我們應該鼓勵平時學有余力的精英同學,不應局限于初中的知識,還可以廣泛涉獵更多更廣的內容”.讓學生主動思考,積極探索,這樣就能站在一個相對的高度去看待問題,這其實就是一種數學核心素養的提升.

