MEMS諧振器的常用閉環驅動控制方法對比分析*

李 志，張 晶，周 嚴，楊欣雨

(1.南京理工大學 機械工程學院·南京·210096；2.中國人民解放軍96962部隊·北京·102200)

0 引 言

微機電系統(Micro-Electro-Mechanical System，MEMS)[1]，也叫做微電子機械系統、微系統、微機械等，是一種尺寸為幾毫米甚至更小的高科技裝置，主要由傳感器、執行器、信號處理與控制電路、通信和電源等器件構成。MEMS諧振器指的是微機電系統中用于振動測量和控制的諧振器件，通常由微加工制造出來，具有很高的靈敏度和精度。MEMS諧振器基于固有頻率和振動模式，通常由一個或多個懸臂梁振子或叉形振子組成，用電路驅動并檢測其振蕩頻率或振幅變化[2]。與傳統的石英晶體諧振器相比，MEMS諧振器具有體積小、功耗低、加工簡便等優點，因此，已被廣泛應用于諸如慣性導航、加速度計、陀螺儀、壓力傳感器、生物傳感器等領域。在MEMS系統中，諧振器與其他微機電部件可以結合成為系統，并通過閉環控制等手段實現高精度和高穩定性的測量與控制[3-4]。MEMS諧振器輸出的頻率信號可與數字電路和計算機直接相連，省去A/D轉換接口，而且頻率信號在傳輸過程中不容易出現失真誤差[5]，因此，具有廣闊的發展前景。

為了提高MEMS諧振器的精度，實現頻率捕捉、跟蹤和幅度控制，需要閉環驅動控制來維持幅值穩定振蕩。其閉環控制系統應具備以下功能[6]：1)上電后，維持梳齒結構工作在諧振頻率處，能夠快速、準確、穩定跟蹤梳齒結構諧振頻率變化；2)當外界環境條件發生變化時，梳齒結構維持穩定的諧振狀態，保證閉環系統的正常工作。

關于MEMS諧振器閉環驅動控制方法的研究，國內外學者主要圍繞提高幅度控制效果和實現相位精確控制這兩個方面給出解決方案。

美國Drapper實驗室開展諧振器的研制工作時間最早，其在2004年提出一種與雙質量塊諧振式加速度計結構對應的接口電路，該電路采用AGC自動調幅方法實現自激驅動[7-8]，利用AGC自動幅度控制方法提供的穩定幅值大大改善了諧振器頻率的穩定性。

2007年，韓國國立大學公布了一種非線性控制的閉環幅度控制電路，并應用在硅微諧振式加速度計和微機械陀螺儀領域，其在相位調整的基礎上可實現完整的閉環驅動以及幅度控制功能。在電路設計中，采用了鎖相環來使電路相位實現閉鎖，以及采用了自動增益來進行幅度控制[9]。該設計實現了閉環驅動電路的相位跟蹤和幅度控制，為閉環驅動電路實現高精度幅值穩定和提高信噪比提供了思路。

2009年，韓國國立大學的S.Sung等[10]提出了一種新型諧振加速度計驅動檢測原理，其通過控制反饋回路的幅值增益來達到自動增益控制的效果，當電路通電時，微弱噪聲信號使回路起振并工作在諧振頻率處，通過全波整流、低通濾波和PI控制功能模塊實現自動增益控制的效果。

國內中北大學的李錦明提出了多種自動增益控制的電路方案，其中直流-交流自動增益控制和交流自動增益控制都在幅度控制性能上有很好的表現[11]。

2014年，東南大學的張印強等[12]以FPGA作為平臺實現閉環驅動控制，采用數字PI算法進行幅度控制，以及采用數字移相控制來滿足回路相位條件。在常溫下進行實驗測試，驅動幅度控制精度達到9×10-5，相比于傳統閉環驅動方法幅度控制效果明顯提升。同年，南京理工大學的楊亮等[13]提出了具有增益補償功能的數字化閉環驅動方法，將設計的增益補償算法，配合自動增益控制環節和鎖相環環節構建了具有增益補償功能的數字化驅動閉環。后續實驗結果表明，振動速度幅值的相對變化量由無增益補償時的7.29%降到了有增益補償時的0.12%，驗證了具有增益補償功能的微機械陀螺數字化驅動閉環可以較大幅度地提高微機械陀螺標度因數的穩定性。

東南大學的楊成等[14]在2015年設計了一種基于FPGA數字化雙閉環驅動控制電路，借助離散域分析方法，該電路實現了數字鎖相環(Digital Phase-Locked Loop，DPLL)和數字自動增益控制(Digital Automatic Gain Control，DAGC)的驅動控制；通過計算出的參數與條件分別建立了基于離散域分析的相位控制模型和幅度控制模型，并進行了仿真驗證。實驗結果表明，驅動幅度控制精度達到了2×10-5，實現了高精度的控制效果。

2015年北京理工大學的丁春燕等[15]提出將模糊PID算法運用在諧振器閉環控制回路中，以PID算法原理為基礎，采用模糊控制理論作為數字化實現方法，并實現了控制系統的參數自整定。通過相關軟件設計完成了PID閉環控制器的調試，并基于模糊控制理論實現了PID控制系統的相關功能。實驗結果表明，系統穩態誤差穩定在0.1%～0.6%之間，穩幅效果良好。

2022年東南大學的劉宸歌在設計MEMS諧振式加速度計控制環路時，基于傳統PID控制方法提出了一種基于果蠅算法改進的模糊PID算法，以減小閉環系統中模糊PID控制的隨機誤差，改進了果蠅算法編碼與尋優步長訓練過程，比較分析傳統模擬PID控制效果和基于優化后的果蠅算法設計的PID控制效果。實驗結果表明，改進了的PID算法與普通模擬PID算法相比，響應速度更快，調節時間減少了120s，說明了改進的模擬PID算法在擾動干擾下比普通PID相比恢復穩定的時間更短，性能更優秀[16]。

研究表明，在自激振蕩環節中引入鎖相環回路來控制相移，或是在檢測端檢測電流輸出時減小相移，可以提高諧振式加速度計的幅度控制效果，實現相位精確控制。此外，還有一些其他的方案，例如使用濾波器、限幅器和自適應控制算法[17]等，不僅能提高控制精度，還可以減小相位干擾和噪聲。本文擬通過對不同驅動方式進行仿真分析，并對直流-交流自動增益控制系統的PI控制參數進行求取，來得到理想的工作曲線，最后將幾種閉環驅動方法仿真結果進行比較分析，總結得出最適用于MEMS諧振器的閉環驅動方法。

1 諧振器模型搭建

以南京理工大學MEMS慣性技術研究中心研制的諧振器結構[18]為例，諧振器通過諧振梁振動頻率發生變化反映外界加速度。諧振器采用雙端固定音叉結構(Double-Ended Tuning Fork，DETF)，由諧振梁及其動梳齒結構組成。在諧振梁的動梳齒兩側對稱分布相等數量的定梳齒，分別定義為驅動梳齒和檢測梳齒。動梳齒和定梳齒各自引出電極，提供直流偏置電壓，使得二者之間形成電壓差，從而構成驅動電容和檢測電容。驅動梳齒由交流電壓驅動，產生周期性變化的靜電驅動力吸引或排斥諧振梁上的動梳齒，使諧振梁按照其固有頻率振動，檢測梳齒敏感到動梳齒產生的電容變化輸出檢測電流。

本文研究的諧振器結構如圖1(a)所示，圖1(b)呈現驅動電壓作用下梳齒結構具體參數示意圖，具體結構參數如表1[19]所示。

(a) 諧振器結構示意圖

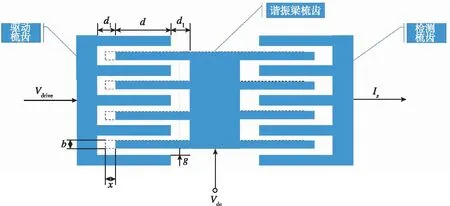
(b) 梳齒結構參數示意圖圖1 諧振器結構及局部梳齒示意圖Fig.1 Resonator structure and local comb diagram

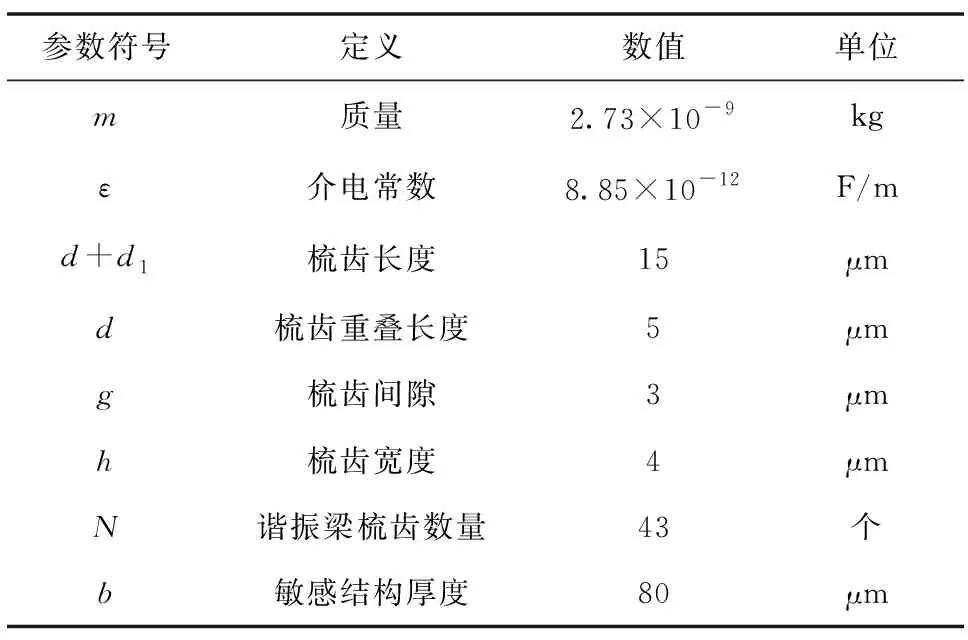
表1 梳齒結構參數Tab.1 Comb tooth structure parameters

該諧振器在靜電驅動作用下進行簡諧振動，其運動學模型可以等效為一個二階質量-阻尼-彈簧系統[20]，其運動微分方程為

(1)

其中，m為諧振器等效質量，c為系統的阻尼，k為等效剛度，F為質量塊受到的靜電驅動力。

對式(1)進行拉普拉斯變換，得到

(2)

為得到驅動電壓到檢測電流的傳遞函數關系式，還應根據諧振器尺寸參數求得驅動電壓到靜電驅動力的傳遞函數和檢測端位移量到檢測電流之間的傳遞函數關系式[21]。

驅動交流電壓到靜電驅動力的傳遞系數為

(3)

其中，N為諧振器梳齒個數，ε為材料的介電常數，h為梳齒寬度，b為敏感結構厚度，g為梳齒間隙，d1為梳齒未重合部分長度，Vdc為直流偏置。

檢測位移到檢測電流之間的傳遞系數為

(4)

聯立式(2)、(3)、(4)可得驅動電壓到檢測電流的傳遞函數為

(5)

得到了驅動電壓到檢測電流的傳遞函數后，即可利用仿真軟件搭建二階系統模型進行后續的仿真處理。式(5)中涉及的具體諧振器參數如表2所示。

表2 諧振器參數Tab.2 Resonator parameters

2 搭建閉環驅動仿真模型

將諧振器輸出的檢測電流進行從電流到電壓的轉換放大并作為驅動電壓反饋到驅動梳齒上的過程即為閉環驅動。諧振器經過真空封裝，品質因數為20402。品質因數越高，越容易產生自激振蕩[22]。除此之外，自激振蕩條件[23]還應滿足環路總增益|AF|=1，環路總相移φ=2nπ ，其中A代表諧振器的傳遞函數，F代表反饋電路傳遞函數。相位條件：檢測端直接檢測梳齒電容變化的電流量，即梳齒電容采用速度檢測模式，這相當于對位移信號的微分，會產生90°的相移，而當靜電力施加在諧振器上時，振動位移信號將滯后驅動信號90°，最終，諧振器從交流驅動電壓到檢測電流的相移為0°。環路增益條件由自動增益控制環路來實現。下文對幾個自動增益控制方法進行仿真分析。

2.1 無自動增益控制的閉環驅動

自激振蕩電路分為無自動增益控制的閉環驅動、自動增益控制的閉環驅動。如圖2所示，在仿真軟件中搭建無AGC自動增益控制的閉環驅動模塊。

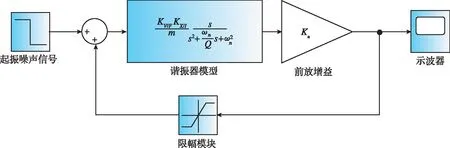
圖2 無自動增益控制的閉環驅動Fig.2 Closed-loop drive without automatic gain control

交流驅動電壓作用到驅動梳齒端產生靜電驅動力，質量塊發生水平運動，右側梳齒電容發生變化產生檢測電流，該電流經過二階跨阻放大電路完成電流-電壓轉化。再經過限幅電路產生限幅方波，將限幅方波加到驅動梳齒端達到正反饋目的，進而產生自激振蕩。該電路需要微弱信號達到起振作用，在仿真軟件中采用階躍信號模塊產生微弱信號。

無自動增益控制的閉環電路結構簡單，容易振蕩，引入噪聲源較少，但是上升時間和調節時間都很長。且因為沒有自動增益控制，當諧振頻率發生變化，在仿真時間2.6s處將諧振頻率由20.5kHz調整到30kHz時，如圖4所示，幅值穩定效果差，容易造成諧振器上非線性振動。因此，無自動增益控制的閉環驅動適用于信號源穩定、動態范圍要求不高的場景。

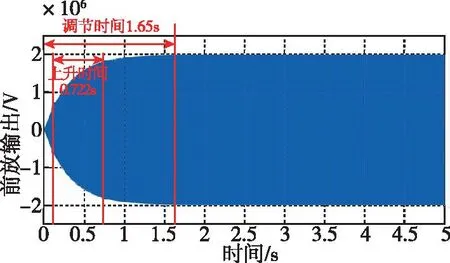
圖3 無AGC的閉環驅動仿真結果Fig.3 Closed-loop drive simulation results without AGC

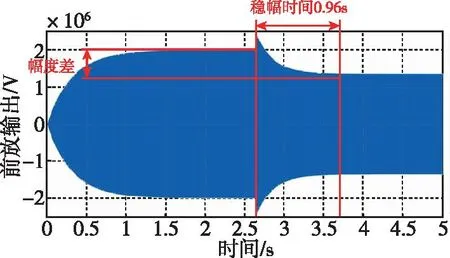
圖4 改變諧振頻率仿真結果Fig.4 Simulation results of changing resonant frequency

2.2 直流-交流自動增益控制的閉環驅動

諧振式加速度計閉環驅動的自動增益控制方法能夠在振動幅度降低時，通過提高驅動電壓來增加靜電驅動力，從而使振幅增大達到負反饋效果。反之，當振幅增加時，通過降低驅動電壓來減小靜電驅動力，從而達到幅值穩定。這里分別對直流-交流自動增益控制方法和交流自動增益控制方法進行仿真分析。

圖5為直流-交流自動增益控制的閉環回路，驅動檢測電流通過前端放大電路輸出電壓信號，電壓信號經過全波整流、低通濾波后與參考電壓相減，再經過PI控制電路輸出控制量，其控制量與經過前端放大電路的電壓信號相乘輸出驅動電壓作用在驅動梳齒上。當振動幅值發生變化時，其AGC回路控制幅值維持在恒定值，PI控制電路可以有效地穩定振幅，且可以改善系統的穩定時間，通過調整PI控制參數，可以使系統阻尼比維持在理想狀態，控制效果有所改善。

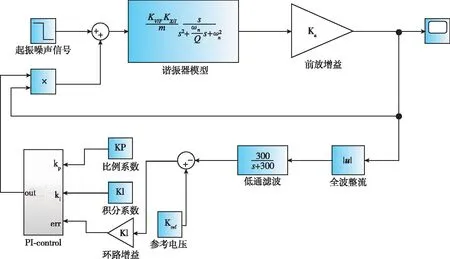
圖5 直流-交流自動增益控制閉環驅動Fig.5 DC-AC automatic gain control closed-loop drive

為了在階躍響應中得到更為直觀的響應曲線，可以將傳遞函數簡化為關于幅值的傳遞函數，只關注幅值變化曲線。

傳遞函數H(s)是諧振器的傳遞函數，當諧振器工作在諧振頻率處時，可以把靜電驅動力到位移關于幅值的傳遞函數寫為[21]

(6)

同時，從交流驅動電壓幅值到交流檢測幅值的諧振器傳遞函數Hamp(s)包括以下三個元素：1)交流驅動電壓到靜電驅動力的傳遞系數KV/F；2)靜電驅動力到位移關于幅值的傳遞函數Famp(s)；3)諧振器振動位移到檢測交流的傳遞函數KI/X。三個元素相關聯，構成諧振器交流驅動電壓幅值到交流檢測幅值的傳遞函數為

(7)

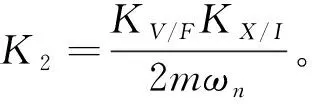
L(s)=KaKuHamp(s)HPI(s)Famp(s)

(8)

PI控制參數設為kp=1，ki=30，環路增益K1待確定，低通濾波模塊的截止頻率為300Hz，前向放大增益設為2×107。將參數代入式(8)可得

(9)

反饋控制系統動態特性取決于閉環系統的極點分布，根軌跡法[24]能夠通過閉環傳遞函數的極點隨開環增益從0至∞變化在s平面上產生的軌跡來確定環路最佳增益。

根據式(9)繪制了如圖6所示的根軌跡圖。

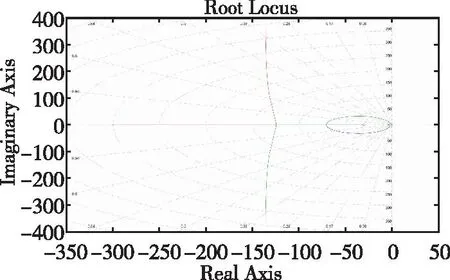
圖6 系統傳遞函數根軌跡圖Fig.6 System transfer function root trajectory graph

由圖6可以看出，系統的特征根都在s平面左側，所以無論環路增益如何變化系統都是穩定的。開環系統在坐標原點有一個極點，為Ⅰ型系統，在輸入為階躍信號的情況下，穩態誤差為0。當環路增益在0.532時，系統阻尼比為0.707，系統性能達到了最佳狀態。

在仿真軟件中搭建仿真模型如圖7所示，當選取環路增益為0.532時，其階躍響應超調量約為12%。

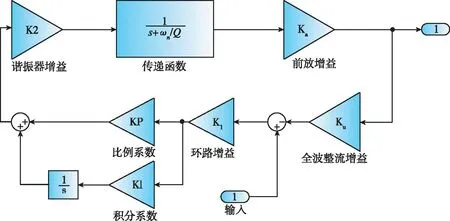
圖7 幅度控制環路仿真模型Fig.7 Amplitude control loop simulation model

將所有系數代入圖5所示的閉環驅動環路，得到的仿真波形如圖8所示。其上升時間和調節時間分別為0.008s和0.214s，相比于無自動增益控制的閉環驅動方式系統響應速度有明顯提升，且因為加入了PI控制電路，響應波形可以通過改變系統參數來改善。當諧振頻率發生波動時，如圖9所示，在2.58s處諧振頻率由20.5kHz調整到30kHz，調整時間為0.105s，幅值無變化。由仿真結果可以看出，該閉環驅動方式較無自動增益控制的閉環驅動方式穩定性更好。

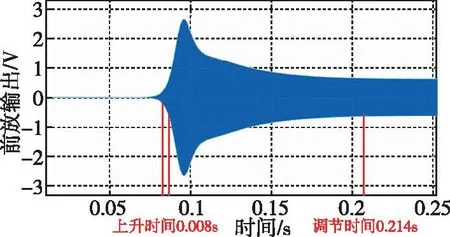
圖8 閉環驅動仿真結果Fig.8 Closed-loop drive simulation results

圖9 改變諧振頻率仿真結果Fig.9 Simulation results of changing resonant frequency

2.3 交流自動增益控制的閉環驅動

直流-交流自動增益控制方法的穩幅效果很好，但其也有一定的局限性：1)器件眾多，不適于整體的小型化發展；2)環路中存在乘法器，會產生較高功耗，不能滿足低功耗目的。但交流自動增益控制的閉環驅動系統簡單、模塊單一、穩幅效果好。

圖10為交流自動增益控制的仿真模型[11]，左側驅動模塊產生靜電驅動力作用在梳齒上產生水平運動，右側檢測梳齒輸出檢測電流，檢測電流通過前置放大電路完成電流和電壓信號轉換，該信號通過增益模塊和限幅模塊轉換為方波信號，然后輸入減法模塊中與前置放大電路輸出信號相減，輸出的差值信號再經過增益模塊和限幅模塊產生方波信號。

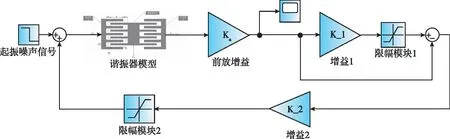
圖10 交流自動增益控制仿真模型Fig.10 Simulation model of AC automatic gain control

其中，k1主要影響方波的波形，當k1越大，方波波形越理想。k2主要影響自激振蕩的調節時間，增大k2數值，輸出波形的上升時間和調節時間明顯縮短。但提高增益會同時放大噪聲信號，不利于降低信噪比。所以增益選取應適量，當k1=2，k2=10時，調節時間為7.035ms，上升時間為1.466ms，如圖11所示。

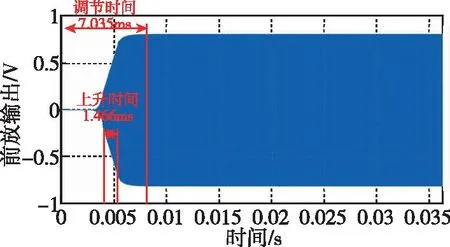
圖11 驅動仿真結果局部放大圖Fig.11 Partial enlarged view of drive simulation results

方波信號的周期和占空比可以控制其平均值，因此可以通過改變占空比(方波寬度)來改變平均值，并控制輸出信號的幅度。具體來說，當輸入信號的幅度大于預設范圍時，將會導致反饋回路的增益系數發生變化，進而改變輸出信號的幅度。此時，可以引入反饋控制，通過更改方波寬度來實現輸入信號的幅度控制，從而達到信號的穩幅效果。

總之，通過交流自動增益控制的閉環驅動并結合方波寬度控制，可以實現諧振器的自適應穩幅效果，提高輸出信號的穩定性和抗干擾能力。

當諧振頻率從20.5～30kHz變化時，其仿真波形如圖12所示，穩幅時間為3.592ms，穩幅效果比較理想。

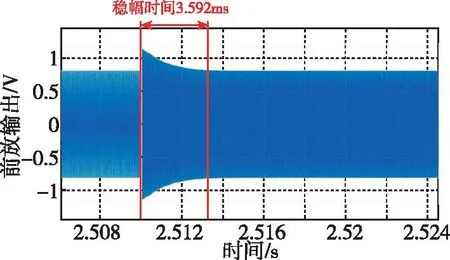
圖12 諧振頻率變化仿真局部放大圖Fig.12 Partial enlarged simulation of resonant frequency changes

2.4 三種閉環控制方法分析比較

對直流自動增益控制、直流-交流自動增益控制和交流自動增益控制方法在仿真中得到的結果進行歸納分析，如表3所示。上升時間和調節時間都表征了系統的響應速度，當上升時間和響應時間越短，系統響應速度越快，穩幅時間反映了閉環驅動回路抗干擾、維持幅值穩定能力，是閉環驅動回路的重要指標[25]。

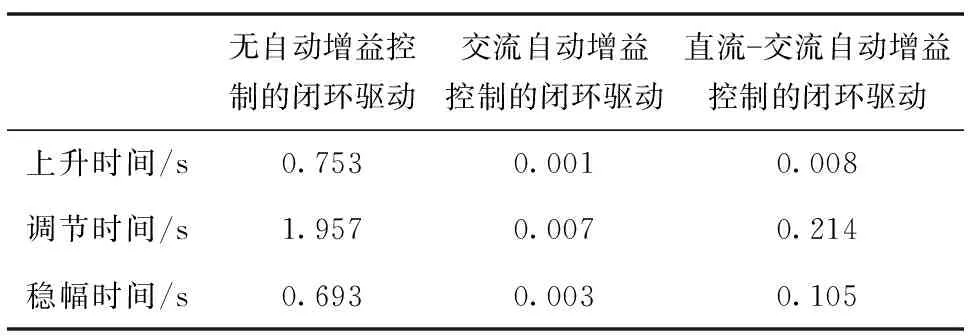
表3 三種驅動方式仿真結果Tab.3 Simulation results of three drive modes

由表3可以看出，無自動增益控制的閉環回路響應速度慢、穩幅效果差；但由于結構簡單，噪聲源少，當信號源不易受到外界影響時，使用無自動增益控制的閉環回路可以更加穩定地接收信號。該方法可以解決在高穩定性要求的場景中，電路因環境因素等干擾引起的偏差問題。該方法不進行信號補償調整，適用于信號源穩定、動態范圍要求不高的情況。交流自動增益控制的閉環驅動響應速度最快，這是因為交流自動增益控制僅有放大模塊和限幅模塊，沒有賦值調制模塊，僅對交流信號進行自動增益控制，相比于直流-交流自動增益控制的閉環驅動減少了系統延時。該方法主要是為了解決在處理包含不同頻段信號時，不同頻段的信號被過度補償導致整體信號失真的問題。只對交流信號進行控制，可以更好地保持整體信號的穩定性和準確性。但實際上，信號中包含噪聲等干擾成分，會導致閉環驅動回路增益系數頻繁變化，進而影響輸出信號的穩定性。而對于直流-交流自動增益控制方法，環路通過PI控制實現幅值穩定，有效提高系統的信噪比。該方法適用于在接收弱信號時，信號的變化范圍比較大，要求輸入信號幅值范圍擴大的場景。

3 結 論

本文對三種閉環驅動方法進行了仿真分析，測量了仿真數據，比較了三種閉環驅動方法的上升時間、調節時間和穩幅效果。對于諧振式加速度計，交流自動增益控制和直流-交流自動增益控制的閉環驅動方法都能很好滿足其工作要求。直流-交流自動增益控制的閉環驅動與交流自動增益控制的閉環驅動相比，信號的穩定性更好，適用于測量精度要求較高的應用場合，在測量加速度、速度、位移等信號時，直流-交流自動增益控制方法更為適用。直流-交流自動增益控制方法可以根據信號的直流和交流分量分別控制反饋回路增益，從而在測量過程中更精確地抑制干擾信號的影響，提高信號檢測的準確性。

本文暫未對噪聲信號對驅動環路的影響進行仿真分析，也暫未考慮實際電路設計中可能會遇到的工程問題，這些將在后續工作中進行詳細研究。諧振式加速度計閉環驅動控制電路的設計和優化是諧振式加速度計研究中的關鍵問題之一，有各種合適的算法和電路設計方案可以參考，未來的研究將繼續探索更加高效和穩定的方案。