基于BP神經網絡的星箭界面動載荷識別

陳樹海， 郭安豐， 吳邵慶， 費慶國

(1. 東南大學 機械工程學院， 南京 211189; 2. 東南大學 土木工程學院, 南京 211189;3. 上海衛星工程研究所， 上海 201109)

星箭界面動態載荷指火箭發射過程中受到橫向載荷的作用，在星箭連接界面上產生的彎矩和剪力，其載荷信息是地面驗證試驗和可靠性評價的重要依據[1]。雖然在星箭連接界面布置力傳感器能夠直接獲取界面動載荷，但它會改變星箭結構的動力學特性，真實星箭結構一般不允許搭載力測量裝置[2]；基于星箭耦合動力學模型開展耦合載荷分析，也能夠獲取界面處的動載荷，但是該方法需要準確的星箭耦合有限元分析模型、可靠的力學環境預示方法以及準確的火箭外載荷輸入[3]。在衛星結構設計時，依靠衛星結構自身的振動響應反演衛星結構受到的基礎加速度激勵，并進一步估計星箭界面動載荷，能夠避免復雜火箭結構的建模和星箭耦合振動分析，有利于實現服役工況下星箭界面動載荷的在線預測。

基于衛星結構響應反演星箭界面動載荷已有一定的研究成果。朱斯巖等[4]利用星箭結構的Craig減縮模型，先由已知的界面自由度加速度時間歷程求解基礎激勵，并重構結構全場加速度響應，最后代入結構動力學方程求解星箭界面動載荷；Craig減縮模型能夠降低載荷識別計算量，但模型誤差也將導致載荷識別結果的更大誤差。張永濤等[5]基于星箭連接環的理論模型和測量應變與界面力的對應關系，提出一種通過實測星箭連接環應變反演星箭界面力的方法；該方法中采用了薄壁圓筒模型近似星箭連接環，連接環的模擬誤差降低了識別結果的精度。尹健等[6]基于B樣條擬合星箭界面動載荷的分布函數，建立了衛星結構加速度與界面分布動載荷的傳遞關系，提出了一種星箭界面環形分布動載荷的識別方法，然而該方法中未能考慮模型誤差的影響；Wu等[7]考慮了星箭界面力學參數的不確定性，提出一種隨機動力學系統上的隨機動載荷識別方法，利用衛星結構振動響應樣本識別了衛星結構底部隨機振動激勵。

利用結構有限元模型開展動載荷反演[8-9]，有限元模型誤差和動載荷識別算法誤差將會疊加，目前只能是利用模型修正技術盡量提高有限元模型的模擬精度[10]，以獲得更加準確的載荷-響應傳遞關系。當星箭結構模型存在局部非線性時，載荷-響應傳遞關系更加復雜，有限元模型模擬精度將進一步下降，造成載荷識別結果的較大誤差。近年來，智能識別算法在載荷識別領域越來越得到重視[11-13]，有望降低模型和識別算法雙重誤差對載荷識別結果的影響。

實際服役過程中，星箭界面采用對接環連接，無法通過直接安裝傳感器測量界面動載荷，但是衛星結構加速度以及星箭界面處的加速度均可以測量。基于BP神經網絡方法的動載荷識別技術一般直接將動載荷-結構響應樣本作為神經網絡訓練的輸入-輸出，在星箭界面動載荷識別問題中難以實現。本文針對星箭界面動載荷識別提出了一個新的思路，即先使用實測星箭界面加速度激勵和衛星結構加速度響應構建的樣本庫來構建兩者之間傳遞關系的神經網絡代理模型，進而利用實測衛星結構加速度響應識別星箭界面加速度激勵，最后將識別得到的星箭界面加速度激勵施加于高保真的衛星結構有限元模型，分析得到星箭界面動載荷。所提出的新方法能夠利用實測數據訓練得到更可靠的逆向代理模型，實現星箭界面動載荷的估計。本文研究有望實現服役狀態下星箭界面動載荷的在線預測。

1 基于BP神經網絡的星箭界面動載荷識別

1.1 衛星結構激勵與載荷的傳遞關系

衛星結構加速度與星箭界面力存在如下關系

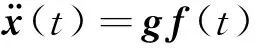
(1)

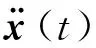
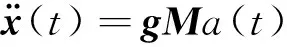
(2)

令G=gM，則G={Gij}表示聯系基礎加速度激勵與結構加速度響應的傳遞關系矩陣，其元素Gij表示在第j個位置作用單位脈沖加速度激勵時在第i個位置的衛星結構加速度響應。利用式(1)或(2)的直接求逆可以識別界面力或基礎加速度激勵，但識別結果會受到結構模型和病態矩陣求逆雙重誤差疊加的影響，當結構模型不準確時，甚至會導致完全無法識別外載荷。

1.2 基于BP神經網絡的載荷識別

動載荷反演的本質是構建響應與載荷的逆向傳遞關系，利用BP神經網絡能夠學習和表征輸入-輸出之間的非線性映射關系，且無需預知描述這種映射關系的數學方程。它采用梯度下降法的學習規則，通過反向傳播修正來不斷調整權值和閾值，最終使網絡的誤差平方和最小。因此，利用BP神經網絡模擬G矩陣中的映射關系，將基于BP神經網絡的動載荷識別方法應用于衛星基礎加速度激勵和星箭界面力識別，能夠有效避免由于衛星結構模型和病態矩陣求逆雙重誤差疊加，提高識別的精度。

本文構建用于識別衛星結構基礎加速度激勵的BP神經網絡結構如圖1所示。

圖1 BP神經網絡結構圖Fig.1 Structural diagram of BP neural network

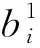
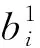
(3)

其次，根據隱含層激活函數σ1(x)計算隱層單元的輸出。隱含層第i個節點的輸出yi根據下式計算

(4)

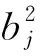
(5)

最后，根據輸出層激活函數σ2(x)進而得到輸出層單元的輸出。輸出層第k個節點的輸出ak計算如下

(6)

根據上述過程可以得到神經網絡的輸出，再根據輸出的結果進行BP神經網絡的誤差反向傳播。此過程將實際輸出與訓練指定輸出之間的誤差反向傳播給網絡上層，來調節各階層權值，最終完成網絡訓練。從輸出層開始，求取各個神經元的輸出誤差，進而采用誤差梯度下降法調節各層網絡的權值和閾值，使得最終調節后的網絡輸出能夠很好地接近預定輸出值。

(7)

各層權值δwk及誤差δbk分別為

(8)

(9)

式中，參數η為調節因子，代表學習速率。

依據上述方法可完成對BP神經網絡各層權值和誤差的調整，每次調整都可以使總誤差函數值下降。通過將調整后網絡的總誤差值與預設的精度進行比較，最終達到精度或者達到最大訓練次數則停止訓練，否則循環迭代不斷調整網絡參數，此調整過程稱為神經網絡學習過程，通過學習過程最終得到滿意的權值、誤差和網絡結構。BP神經網絡構建流程如圖2所示。

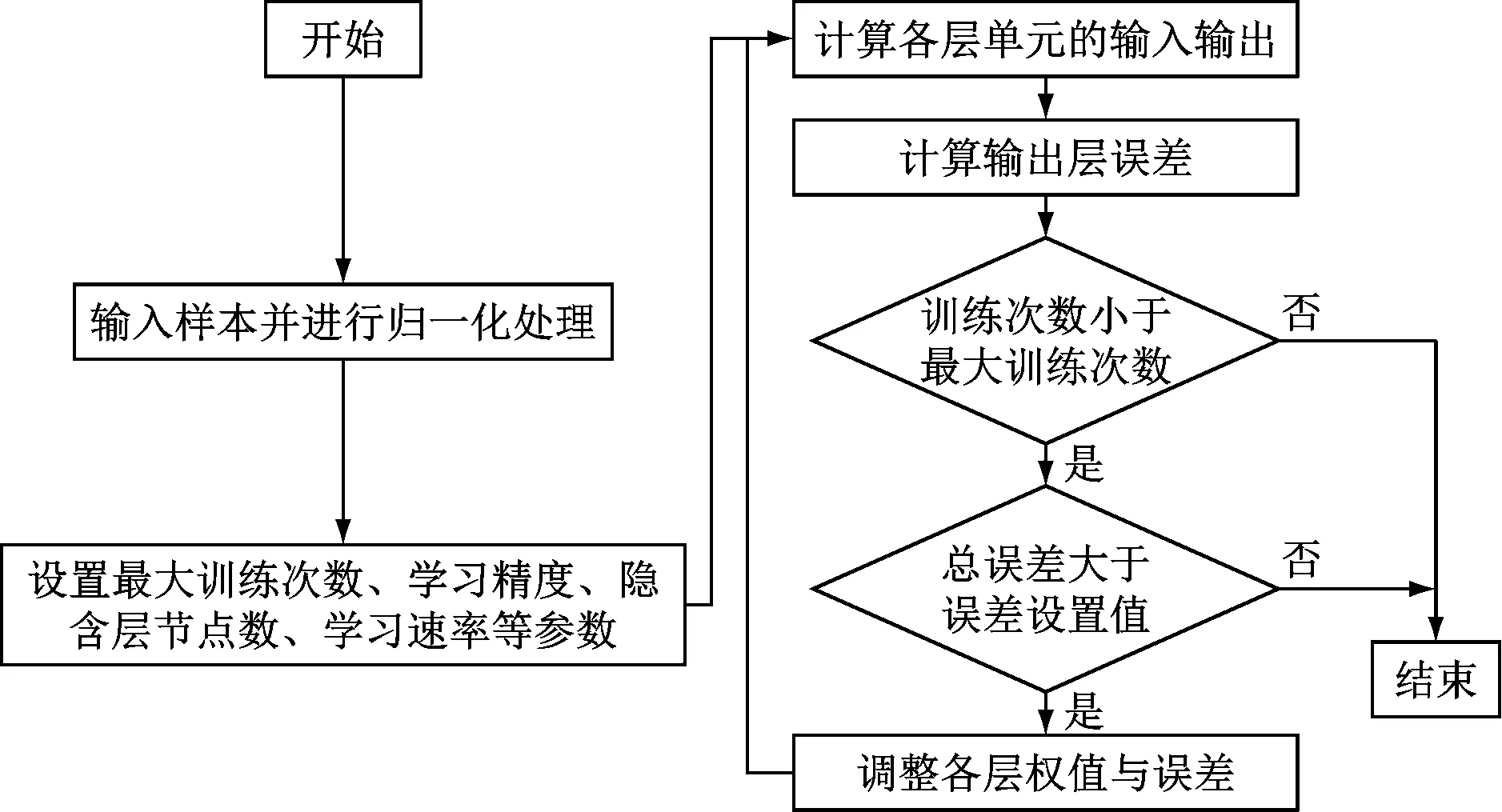
圖2 BP神經網絡構建流程圖Fig.2 Flow chart of BP neural network construction

基于BP神經網絡的星箭界面動載荷反演步驟如下:

(1) 建立訓練樣本并進行歸一化處理。仿真算例中，基于衛星結構有限元模型開展仿真分析獲取樣本；試驗驗證中，直接采用實測響應作為輸入-輸出樣本。基于衛星結構，取基礎加速度激勵與結構加速度響應信號形成訓練樣本集合，其中70%數據作為訓練集，15%數據作為驗證集，15%數據作為測試集。訓練集主要是對數據樣本進行模擬擬合，驗證集負責尋找最優的網絡深度，測試集負責測試最終模型的泛化能力，即預測的準確性。

(2) 明確最大訓練次數、學習精度、學習速率以及各層節點數等參數。本文所建立的BP神經網絡，最大訓練次數為10 000次，學習精度為1×10-7，學習速率為0.01，輸入層節點數為n，分別為當前時刻以及前n個時刻的響應信號。輸出層節點數為1，即當前時刻的基礎加速度激勵。相應的隱含層單元節點數依據經驗公式取為log2n[14]。

(3) 開展動載荷識別。結合實測衛星結構加速度響應數據和訓練得到的BP神經網絡，識別得到衛星結構上的基礎加速度激勵，并將基礎加速度激勵作用于高保真衛星結構動力學模型，獲取星箭界面動載荷。

2 仿真算例

2.1 衛星結構有限元模型

如圖1(a)所示衛星結構由法蘭盤、主承力筒、側板、隔板、L型壓條及M3螺釘連接件組成。構件材料和尺寸如表1所示。衛星結構上各部件采用六面體實體單元建模。采用等效線性化的薄層單元來模擬各部件之間的螺栓連接和接觸。衛星結構有限元模型如圖3(b)所示。

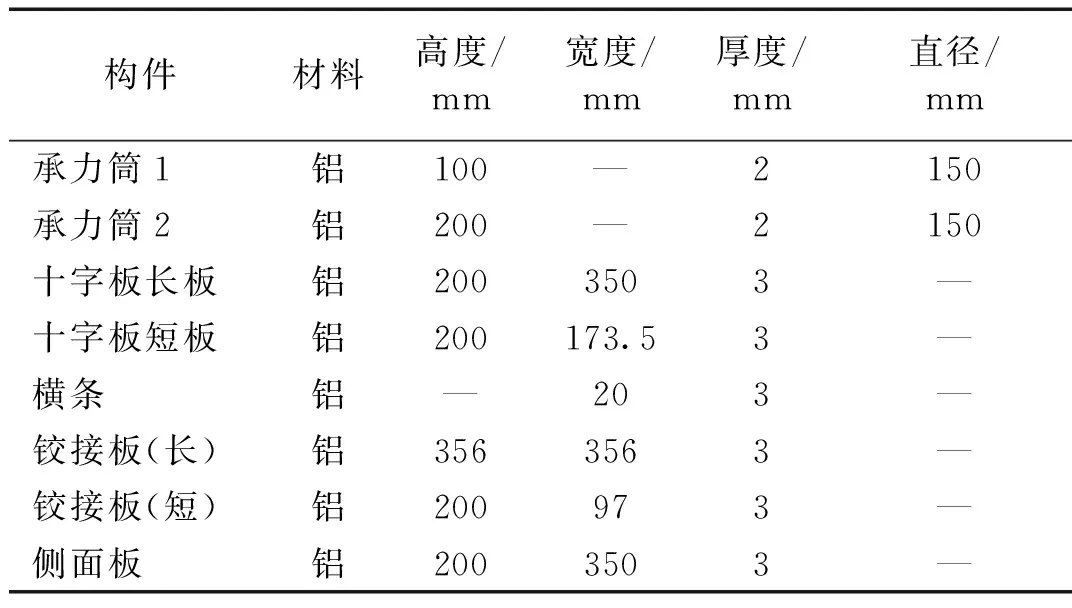
表1 衛星結構主要構件尺寸Tab.1 Dimensions of the main components in the satellite structure

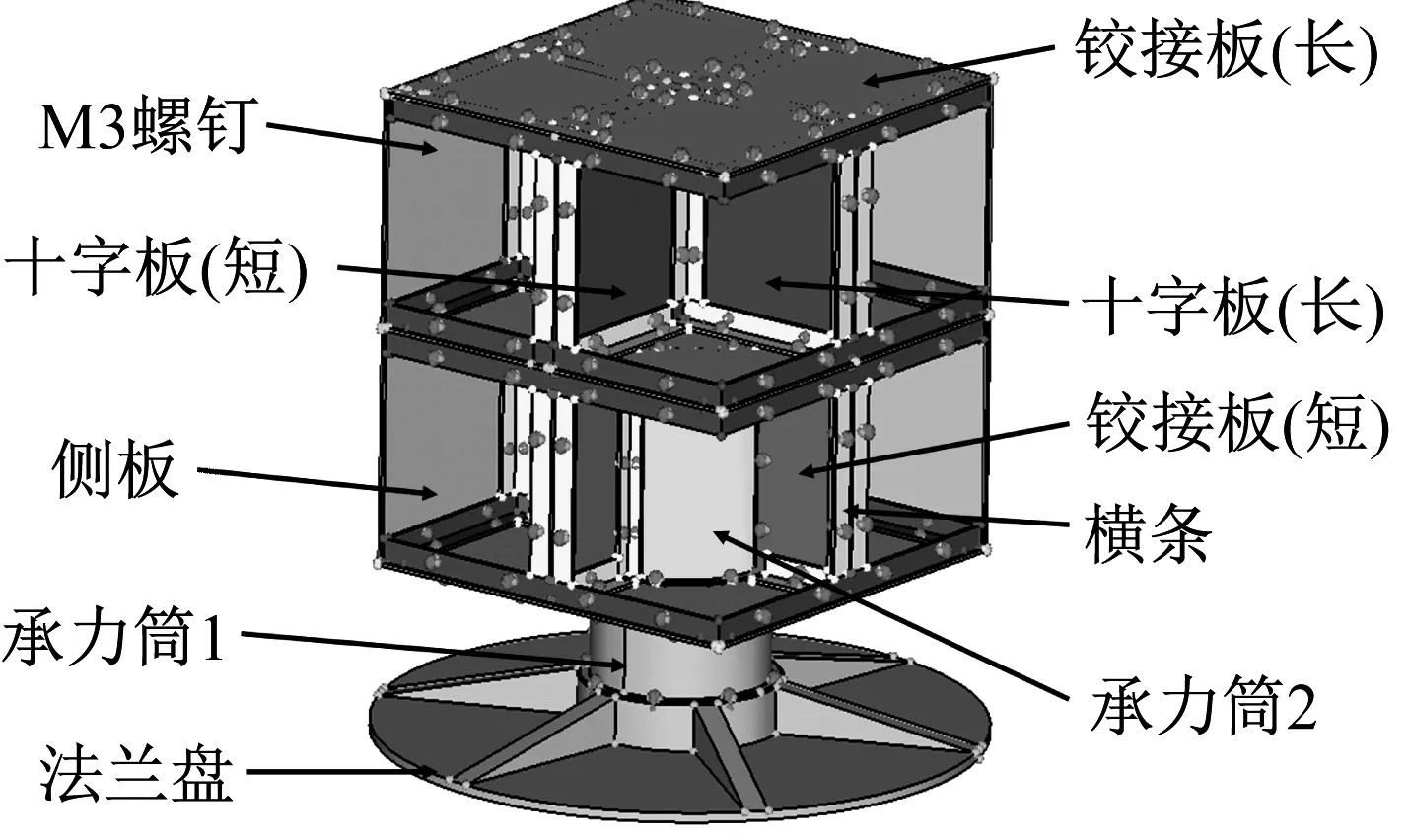
(a) 幾何模型

(b) 有限元模型圖3 衛星結構及有限元模型Fig.3 Satellite structure and finite element model

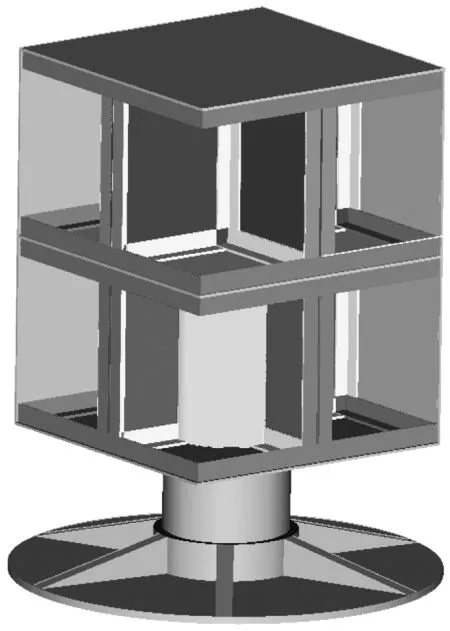
實際服役狀態下的星箭界面動態載荷是難以直接測量的。本研究設計了如圖4(a)所示的力測量工裝，用于實驗室條件下測量振動試驗中振動臺與衛星結構之間傳遞載荷，以驗證本文方法識別得到的星箭界面動載荷的有效性。力測量工裝中包含衛星結構與振動臺的連接裝置以及用于測量傳遞載荷的力傳感器；利用六個力傳感器連接上方法蘭盤和下方底座，底座通過M16螺栓與振動臺臺面連接。力測量工裝各部件的材料和尺寸如表2中所示。建立如圖4(b)所示力測量工裝有限元模型，其中結構件和力傳感器采用實體單元模擬，各螺栓連接和接觸部位采用薄層單元模擬。圖5中給出了帶力測量工裝的衛星結構有限元模型。

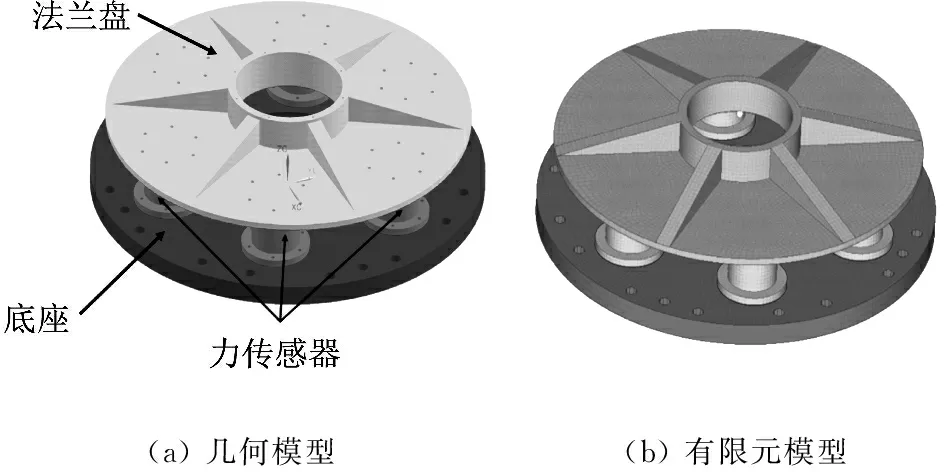
圖4 力測量工裝及其有限元模型Fig.4 Force measuring tooling and its finite element model

圖5 帶力測量工裝的衛星結構有限元模型Fig.5 Finite element model of the satellite structure with force measuring tooling

表2 力測量工裝材料及尺寸Tab.2 Material and dimensions of the force measuring tooling

2.2 正弦激勵工況

選取正弦基礎加速度激勵的頻率為70 Hz，介于帶力測量工裝的衛星結構模型的第1階和第2階固有頻率之間，振動幅值為0.5 m/s2，采樣頻率設定為512 Hz。基礎加速度激勵通過大質量法施加在力測量工裝結構有限元模型底部，如圖5所示。

通過有限元分析得到測點處結構的仿真加速度響應。測點位置與試驗模型測點1的位置相同，測點響應樣本總數設定為3 072，其中70%數據作為訓練集訓練網絡，15%數據作為驗證集，15%數據作為測試集。利用訓練獲得的BP神經網絡，以t,t+1,…,t+19時刻的加速度響應為輸入，即可識別t時刻的基礎加速度激勵。基礎加速度激勵識別值與參考值的對比如圖6所示。由圖可知，本文的方法能夠由衛星結構加速度響應精確識別衛星底部基礎加速度激勵，激勵識別值和參考值之間的均方根誤差趨向于0，其中均方根誤差(root mean square error，RMSE)的計算由下式定義

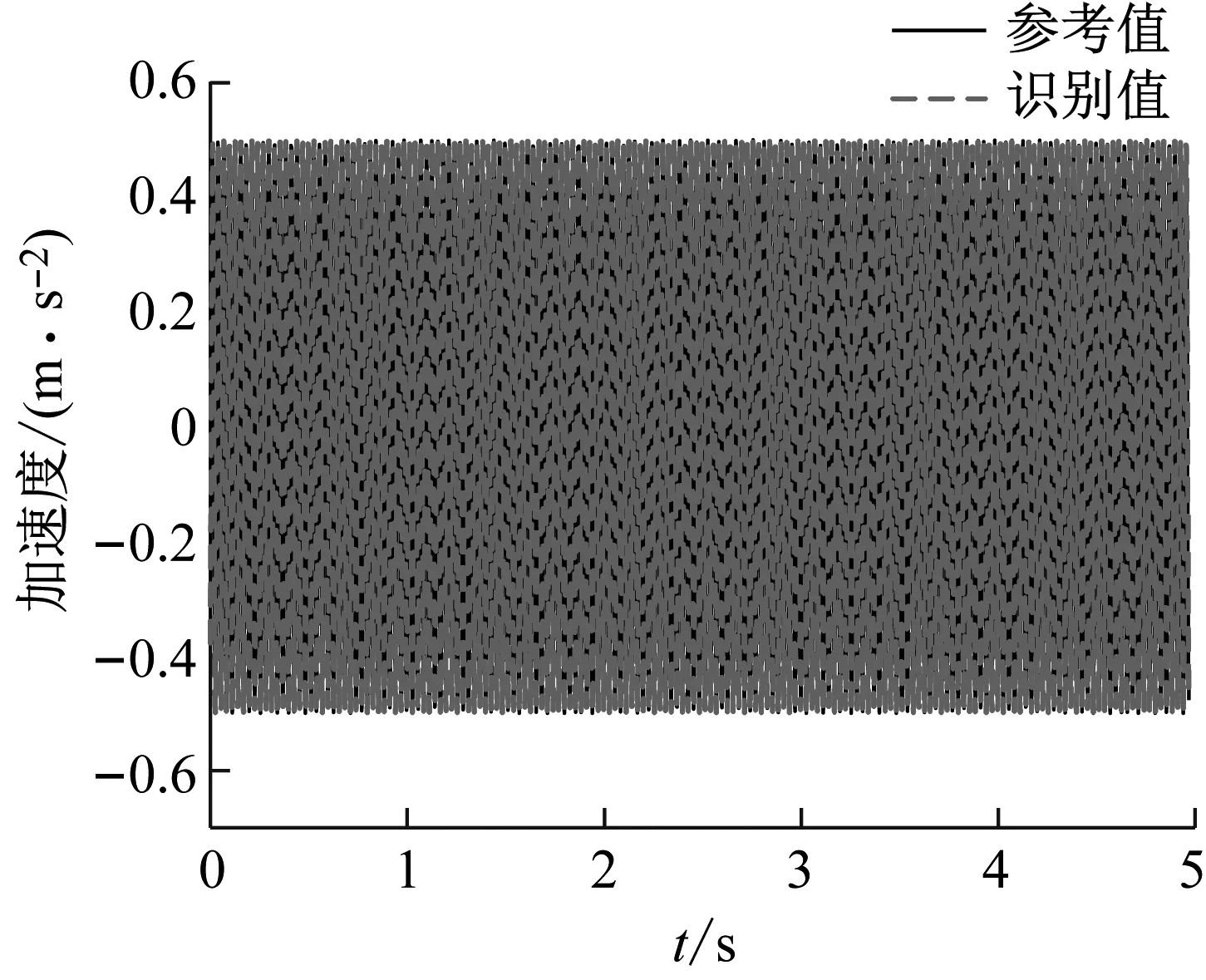
(a) 整體對比

(10)

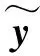
為了研究該識別算法的抗噪聲干擾能力，將仿真計算得到的衛星結構加速度響應信號分別添加2%、10%、20%的噪聲，使用激勵-帶噪聲響應樣本集訓練得到的神經網絡開展基礎加速度激勵識別。信號添加噪聲如下式所示

Yerr=Ycal+lnoise·std(Ycal)·rand(-1,1)

(11)

式中，Ycal和Yerr分別表示加噪聲前后的響應樣本；lnoise表示噪聲水平；std(·)表示標準差；rand(·)表示隨機擾動。

圖7中給出了添加20%噪聲工況下本文方法的識別結果。表3中給出了不同噪聲水平下基礎加速度激勵的識別誤差。結果表明，本文方法在加速度響應受不同程度噪聲干擾的情況下均能夠準確識別基礎加速度激勵，識別誤差隨著噪聲干擾的增大略有增加，方法具有更好的抗噪聲能力。

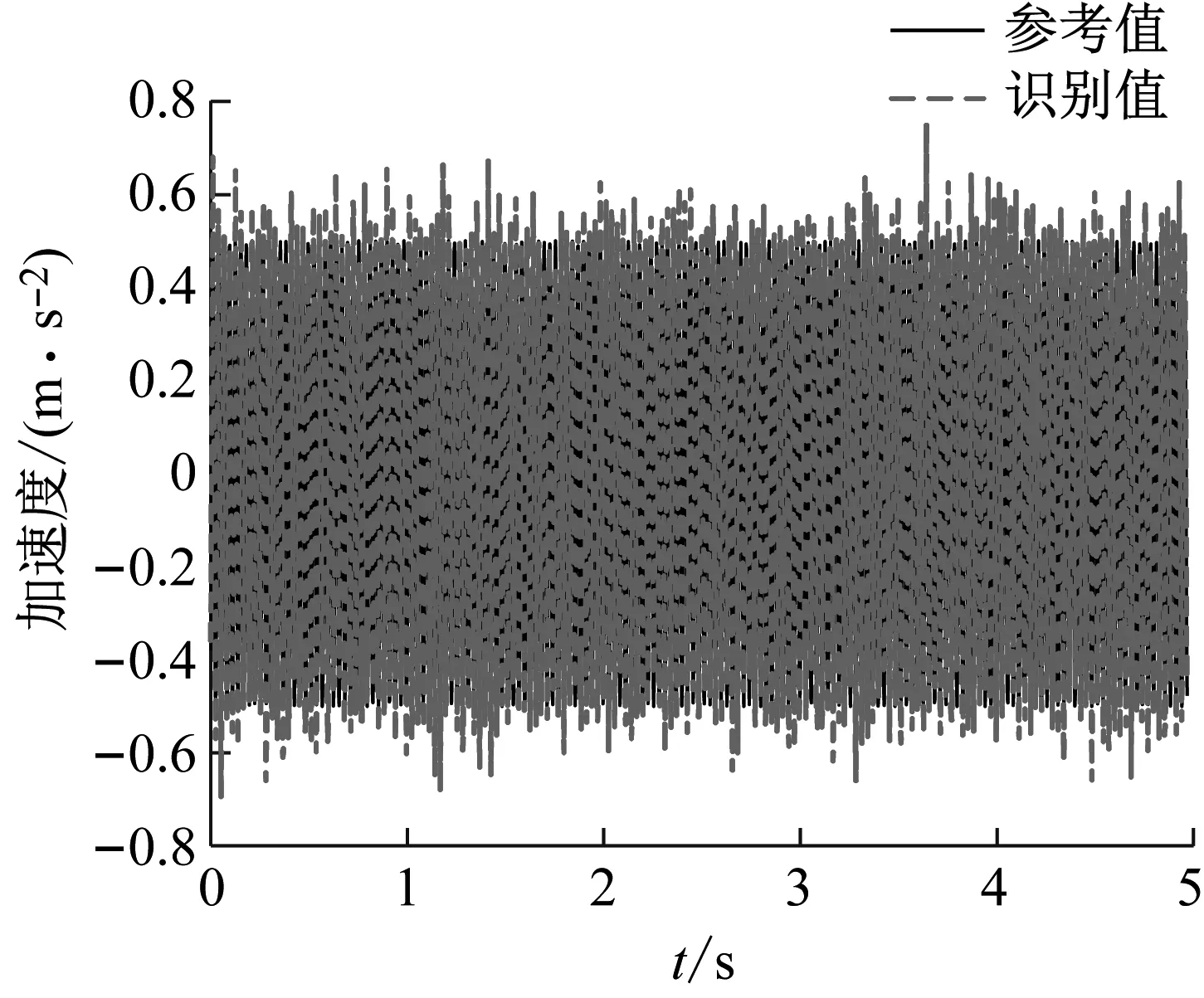
(a) 整體對比

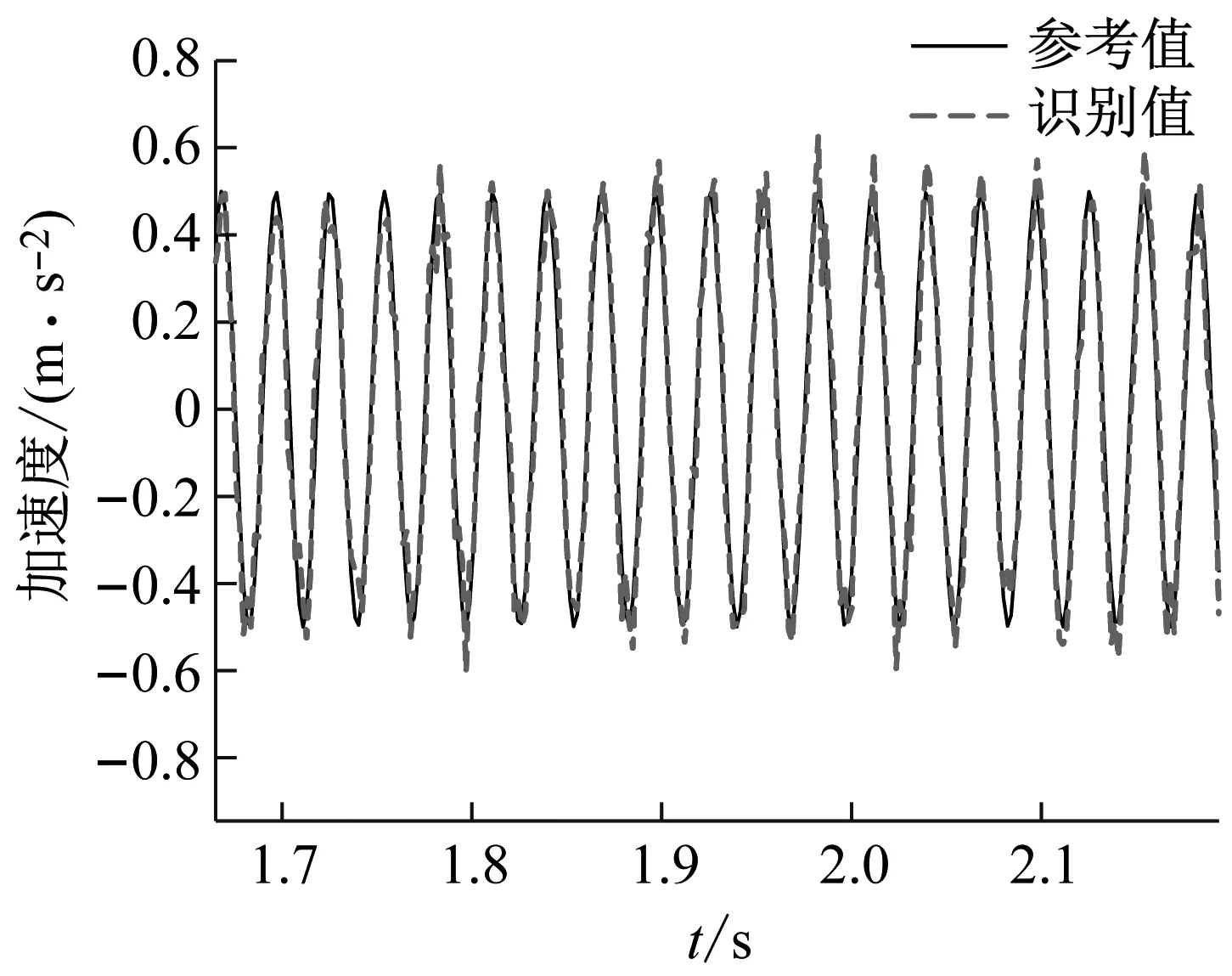
(b) 局部放大圖7 正弦基礎加速度激勵識別結果(20%噪聲)Fig.7 Identification results of sinusoidal basic acceleration excitation (20% noise)

表3 不同噪聲水平工況正弦基礎加速度激勵識別誤差Tab.3 Identification errorsin sinusoidal basic acceleration excitation under different noise level

2.3 隨機振動工況

實際衛星結構常承受隨機振動激勵，利用正弦激勵-結構響應樣本庫訓練得到的神經網絡模型難以用于隨機振動激勵識別。因此本節開展基于隨機激勵-結構響應樣本庫的神經網絡模型訓練和基于衛星結構加速度響應的隨機基礎加速度激勵識別。

參考隨機基礎加速度激勵的功率譜密度函數如圖8所示，激勵頻段為1～100 Hz。利用諧波疊加法得到隨機基礎加速度激勵的樣本，與2.2節中類似，開展帶力測量工裝衛星結構的振動分析，建立隨機激勵-結構響應樣本庫。

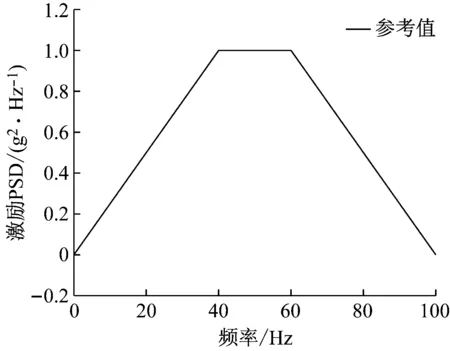
圖8 隨機基礎加速度激勵功率譜密度圖Fig.8 Power spectral density of the random base acceleration excitation

圖9中給出了利用仿真衛星結構加速度響應和訓練后得到的神經網絡模型識別的衛星底部隨機基礎加速度激勵與參考值對比。結果表明了該識別模型對隨機基礎加速度激勵識別的有效性。進一步，為驗證基于隨機激勵-結構響應樣本庫訓練的神經網絡識別模型的普適性，將該識別模型用于2.2節中正弦激勵的識別，識別結果如圖10所示。結果表明該模型也能夠較準確地識別正弦激勵，識別結果的均方根誤差8.489 5；反之，利用正弦激勵-響應構建的神經網絡識別模型則無法適用于隨機基礎加速度激勵的識別。

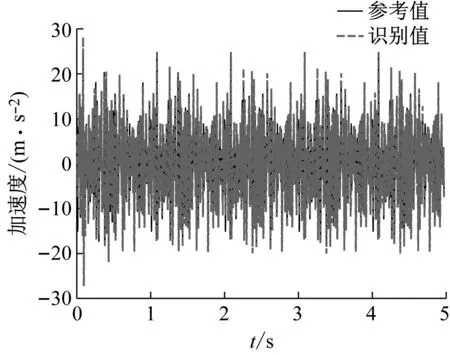
(a) 整體對比

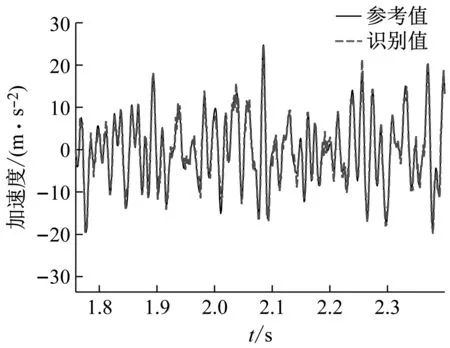
(b) 局部放大圖9 隨機基礎加速度激勵識別結果Fig.9 Identification results of random base acceleration excitation

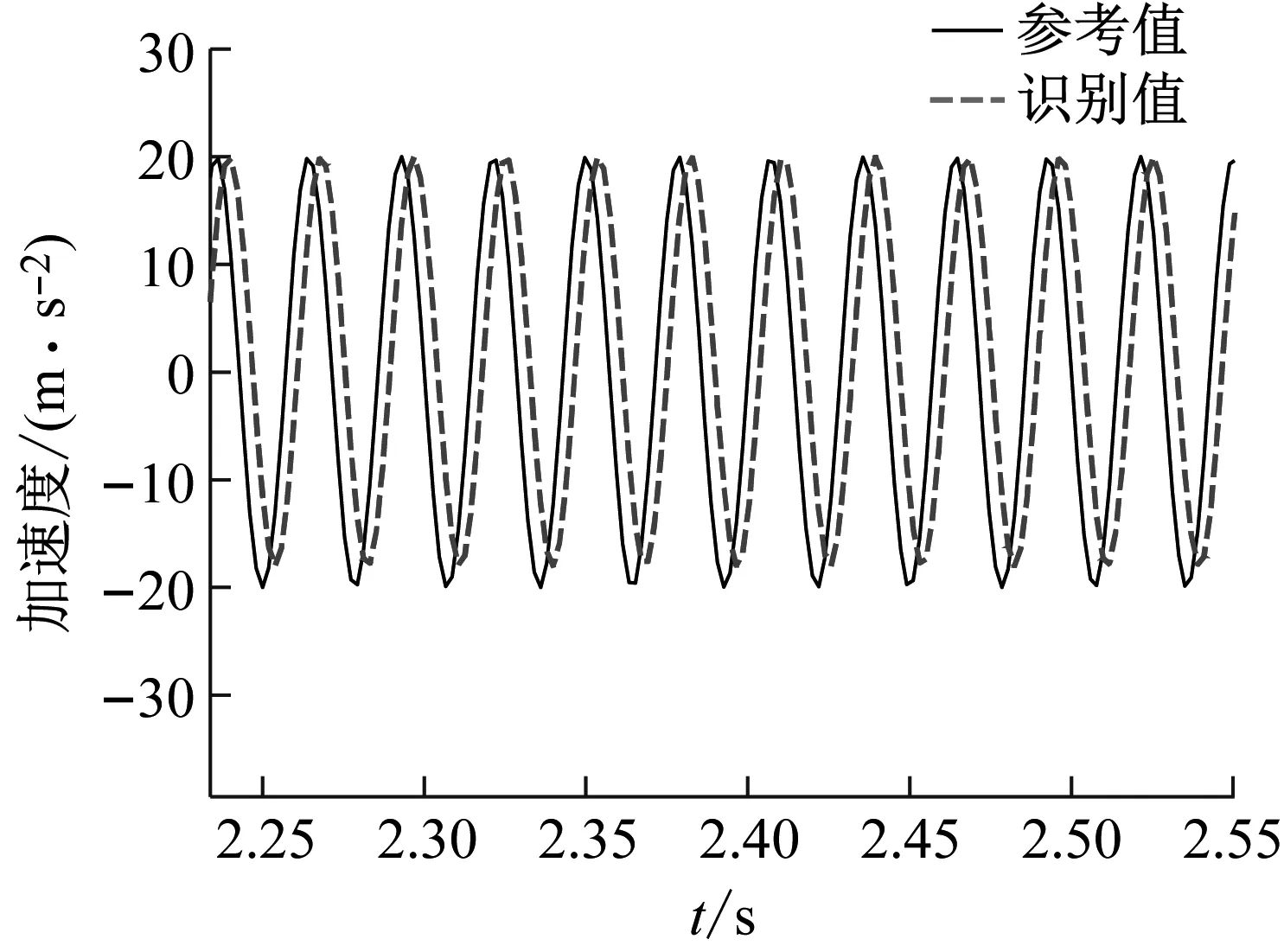
圖10 利用隨機激勵-響應神經網絡模型識別正弦激勵Fig.10 Identified sinusoidal excitation by using the random excitation-response neural network model

3 基礎加速度激勵和界面動載荷識別試驗驗證

3.1 振動試驗系統

為驗證本文提出的載荷識別方法。搭建如圖11所示試驗系統。衛星結構模型底端串聯力測量工裝，固定在振動臺臺面上。在衛星結構上施加橫向基礎加速度激勵，開展結構振動試驗，利用振動臺面加速度數據和衛星結構頂部測點加速度響應訓練載荷反演的神經網絡模型，開展基于實測結構加速度信號的基礎加速度激勵識別并利用實測振動臺面加速度驗證；同時，將識別獲得的基礎加速度激勵作用于結構有限元模型，計算振動臺與衛星結構連接界面間的傳遞載荷，利用力傳感器測量得到的振動臺與衛星結構間傳遞載荷驗證識別的界面動載荷。

圖11 衛星結構基礎加速度激勵試驗圖Fig.11 Baseacceleration excitation test of the satellite structure

值得注意的是，實際星箭連接界面上的動載荷應該連續分布的。但由于分布動載荷的測量存在較大困難，本研究在試驗驗證中，采用了六個三向力傳感器測量得到的集中載荷等效星箭界面上的連續分布動載荷，并利用動載荷識別值與實測值對比來驗證識別方法的有效性。試驗中共有6個加速度信號采集通道以及18個力信號采集通道。振動臺在水平方向激振，載荷工況有兩種：分別是頻率為70 Hz，大小為0.5g的正弦激勵以及頻率范圍為5～100 Hz，大小為0.2g的正弦掃頻激勵。

3.2 識別結果

利用圖11中測點1采集得到的衛星結構加速度響應信號以及振動臺面實測加速度激勵構成的樣本，訓練用于載荷識別的神經網絡；進一步利用實測衛星結構加速度反演基礎加速度激勵。正弦激勵以及正弦掃頻工況下振動臺面的加速度激勵識別結果分別如圖12和13所示。結果表明：基于本文方法構建的神經網絡識別模型能夠準確的識別振動臺面在正弦和掃頻工況下的加速度激勵，識別結果的均方根誤差分別為0.001 7和0.005 9。利用實測衛星加速度響應和振動臺面加速度激勵信號訓練神經網絡識別模型，能夠免去衛星結構有限元建模和模型修正環節，同時能夠一定程度上避免結構有限元模型誤差對基礎加速度激勵識別結果精度的影響。

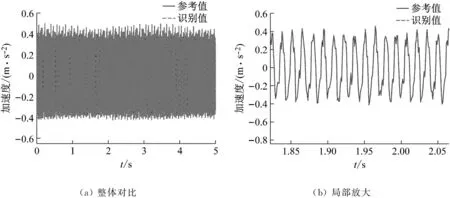
圖12 正弦激勵下振動臺面加速度激勵識別結果Fig.12 Identification results of acceleration excitation on shaking table surface under sinusoidal excitation

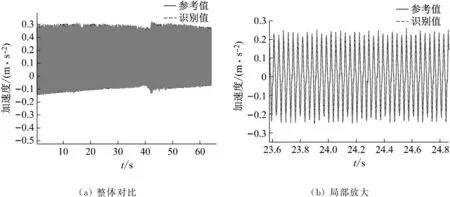
圖13 正弦掃頻激勵下振動臺面加速度激勵識別結果Fig.13 Identification results of acceleration excitation on shaking table surface under swept-sin excitation

將基于神經網絡方法識別得到的振動臺面加速度激勵施加于帶力測量工裝的衛星結構有限元模型，可以計算得到力測量工裝處的傳遞動載荷；利用得到的六個力傳感器位置處載荷時程進一步計算振動臺與衛星結構之間傳遞的六自由度動載荷，驗證界面傳遞六自由度載荷識別結果的精度。由于振動臺加速度激勵為沿x方向的水平激勵，六自由度載荷中，沿x方向的水平合力與繞y軸方向的彎矩為主要的載荷成份。圖14和圖15中分別給出了正弦激勵和正弦掃頻激勵下x，y方向合力以及繞y軸彎矩的識別值與試驗參考值之間在某一個時段的對比結果。結果表明：識別得到的界面動載荷均具有良好的精度，證明了本文提出的界面動載荷識別方法的有效性。正弦激勵工況中三個動載荷識別值與試驗值峰值誤差分別為0.923 8，0.082 9，0.016 1；掃頻激勵工況中三個動載荷識別值與試驗值峰值誤差分別為0.705 9，0.326 3，0.129 4。圖中顯示載荷識別值與參考值之間存在一定的相位差，可能的原因是力傳感器測量信號存在大量噪聲，濾波后存在相位漂移，通過提高力信號測量精度有望實現更小的識別誤差。

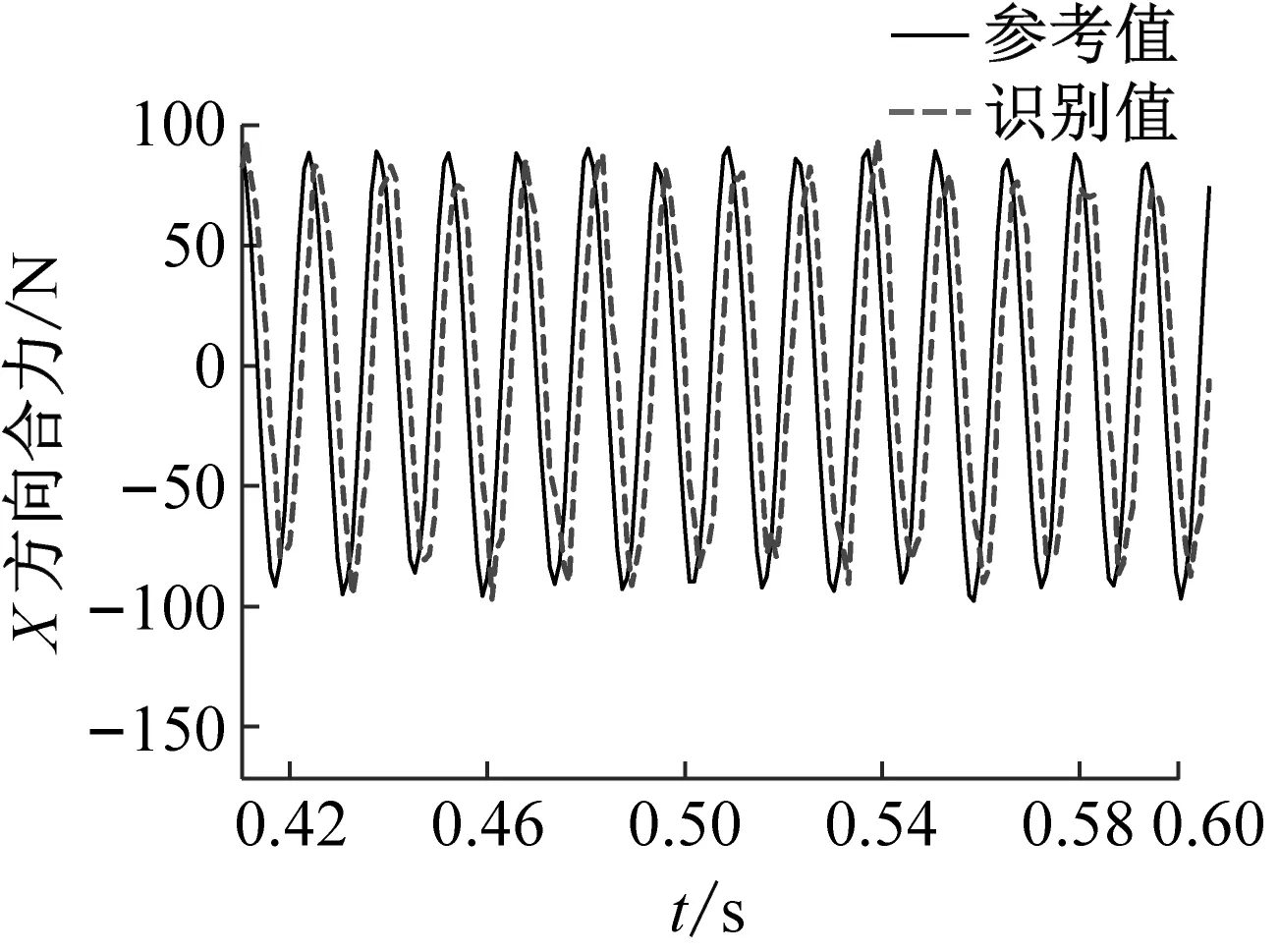
(a) x方向合力

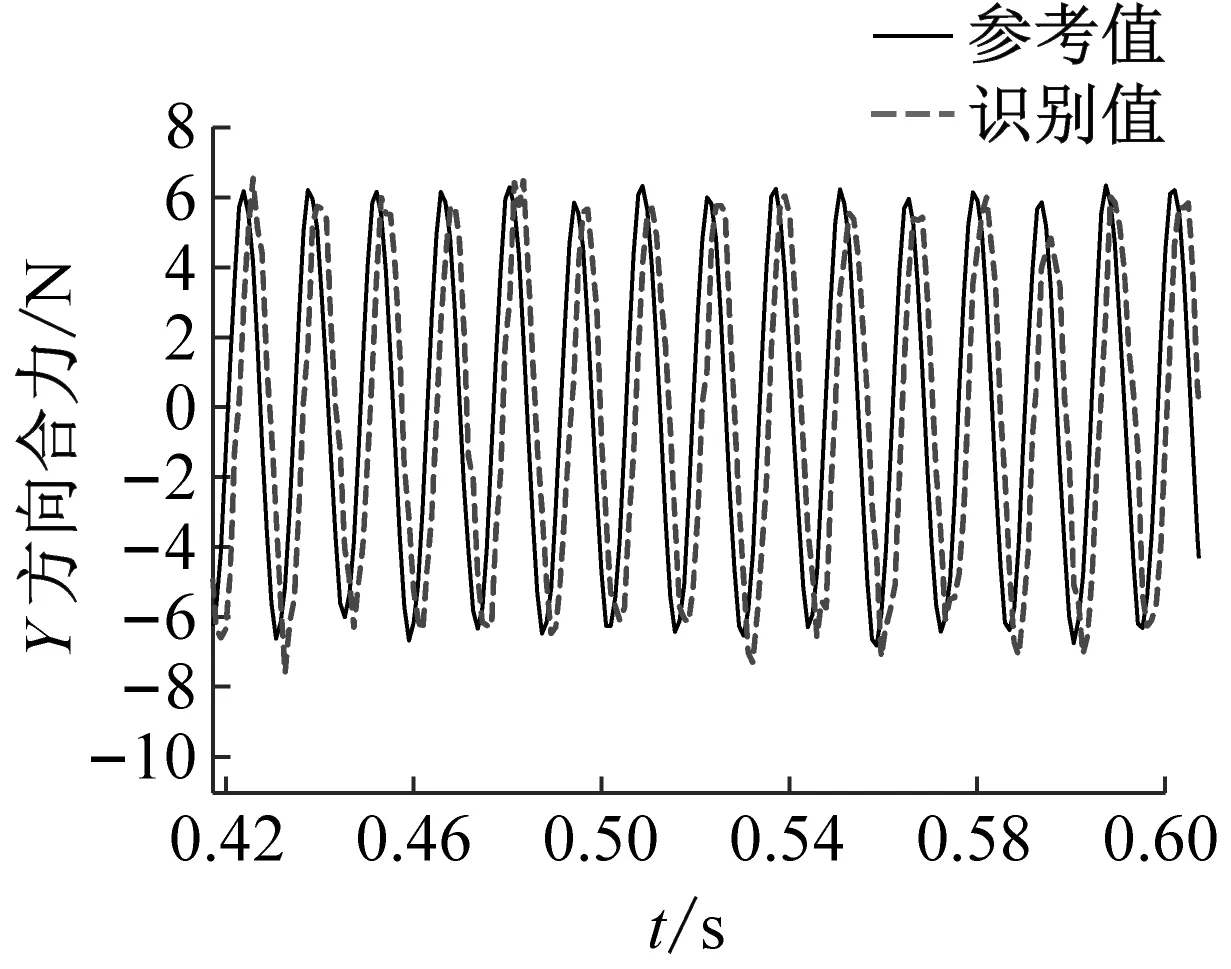
(b) y方向合力

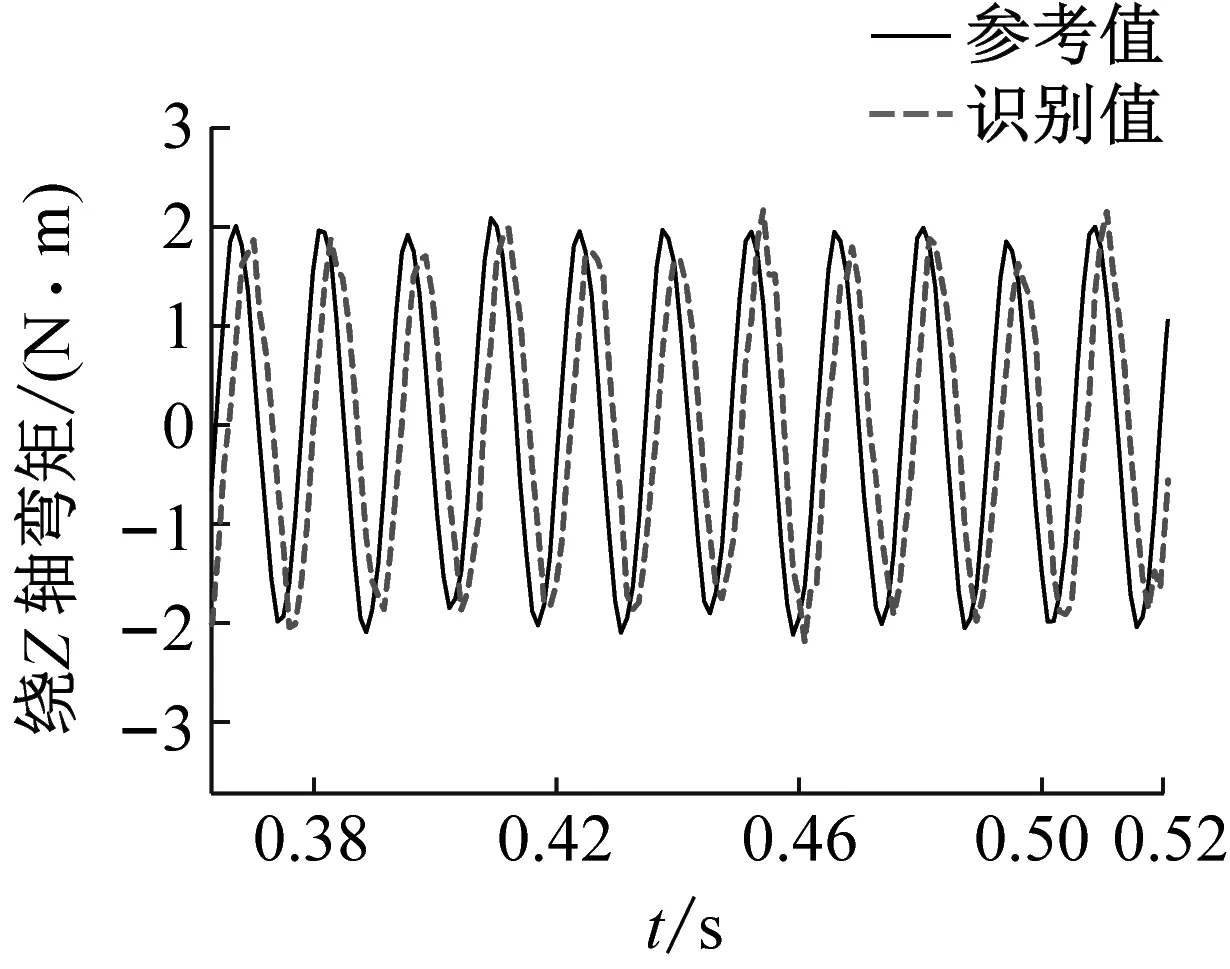
(c) 繞z軸彎矩圖14 正弦激勵下部分六自由度動載荷識別值與實測值對比Fig.14 Comparison of the identified and measured partial six degree-of-freedom dynamic load under sinusoidal excitation

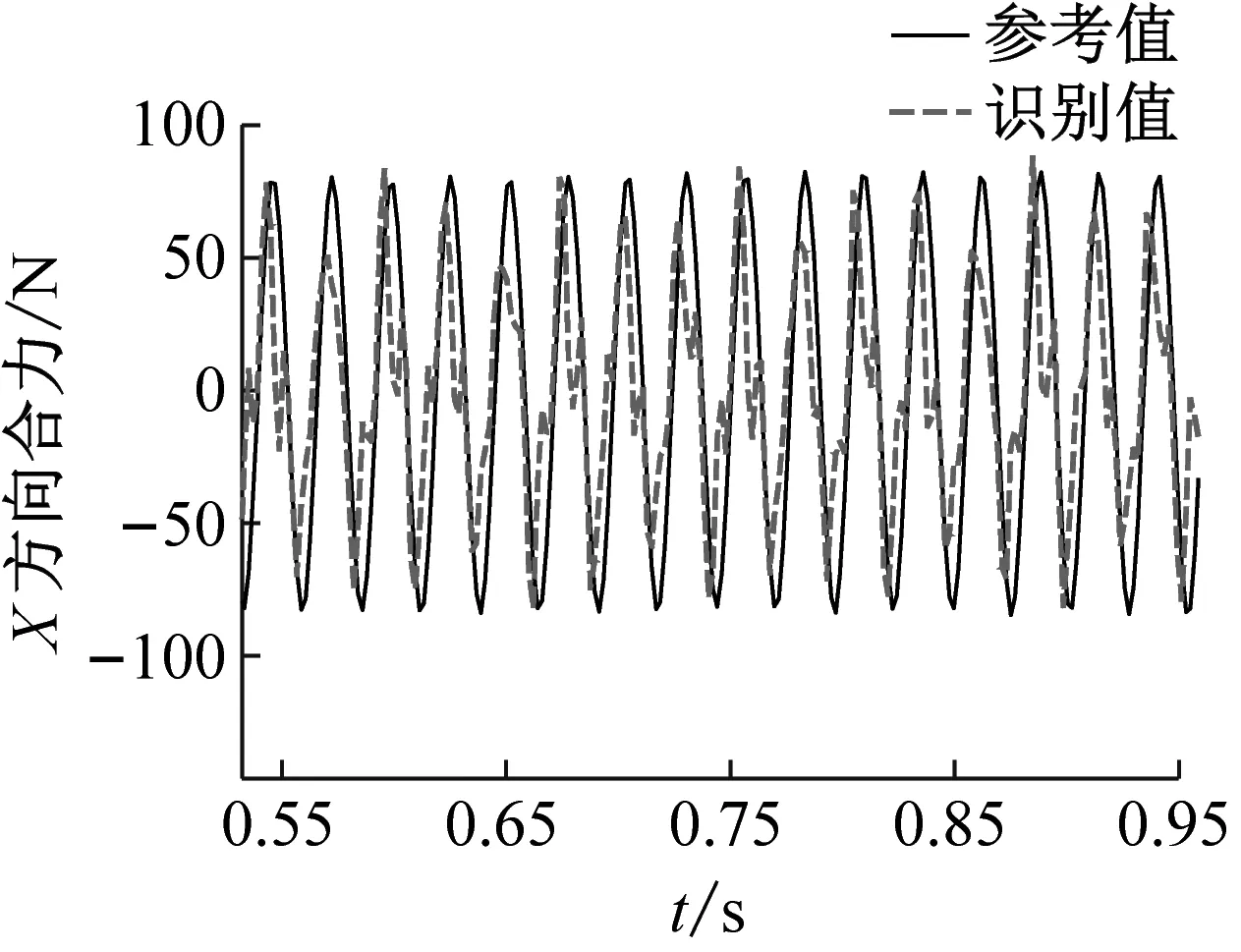
(a) x方向合力

(b) y方向合力

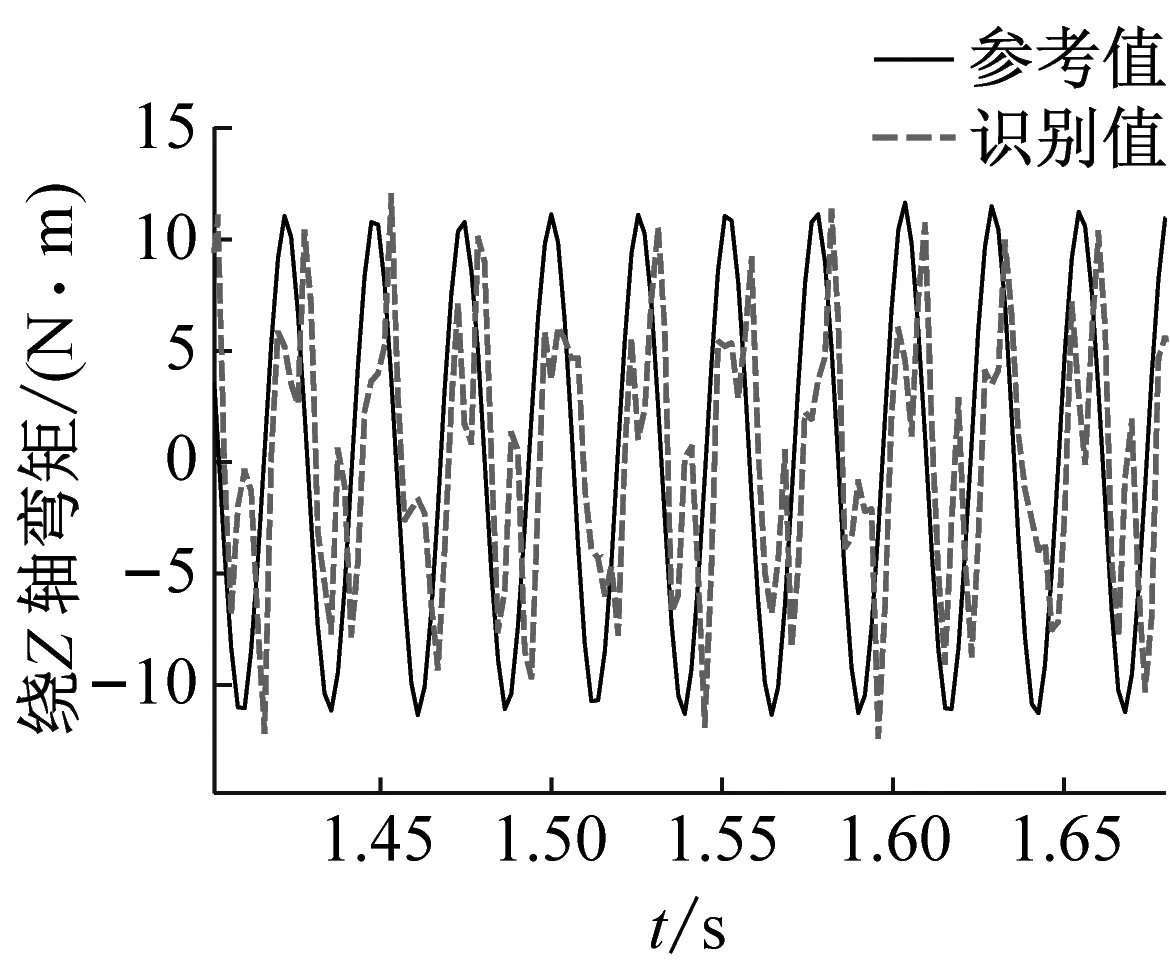
(c) 繞z軸彎矩圖15 正弦掃頻激勵下部分六自由度動載荷識別值與實測值對比Fig.15 Comparison of the identified and measured partial six degree-of-freedom dynamic load under swept-sin excitation

4 結 論

本文基于衛星結構加速度響應和星箭界面加速度激勵構建了激勵-響應樣本數據庫，利用BP神經網絡訓練界面處加速度激勵-衛星結構加速度響應間的傳遞關系，從而建立了星箭界面處加速度激勵的識別模型，并進一步將識別得到的加速度激勵施加于高保真衛星結構有限元模型，實現了基于BP神經網絡模型的星箭界面動載荷的識別。開展了仿真和試驗研究，驗證了方法的有效性。主要結論如下：

(1) 利用激勵-響應樣本庫建立的神經網絡訓練模型能夠準確的反演衛星結構基礎加速度激勵，該方法具有良好的噪聲魯棒性。利用反演得到的基礎加速度激勵和衛星結構有限元模型，能夠準確預測星箭界面動載荷。

(2) 用于動載荷識別的神經網絡模型訓練中，樣本庫構建至關重要；基于寬頻隨機振動工況下的激勵-響應樣本庫構建的神經網絡模型的普適性更好，能夠高精度完成定頻正弦激勵的識別，反之則不能。

(3) 衛星發射過程中，星箭對接面附近的加速度和衛星結構局部加速度響應均可測，本文的方法有望實現服役狀態下的星箭界面動載荷預測。