框架-分布搖擺芯筒-核心筒結構體系力學模型及耗能減震性能分析
陳易飛, 何浩祥, 蘭炳稷, 孫澔鼎
(北京工業(yè)大學 工程抗震與結構診治北京市重點實驗室,北京 100124)
隨著經(jīng)濟和科技水平的發(fā)展,高層建筑結構的數(shù)量日益增多,形式趨于多樣化且設計水平也不斷提高[1-2]。框架-核心筒(Frame-core tube,F(xiàn)CT)結構體系是目前高層建筑中應用較為廣泛的一種形式,該結構由框架和核心筒組成了雙重抗側力體系,核心筒因剛度較大作為第一道抗震防線,而外圍框架則作為第二道防線[3],F(xiàn)CT結構體系示意圖如圖1(a)所示。
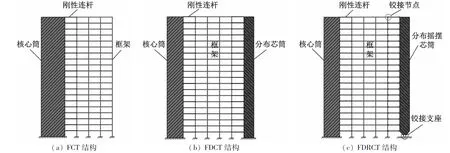
圖1 結構體系示意圖Fig.1 Schematic diagram of structure system
在進行FCT結構抗震設計時,為了提高整體抗側剛度,設計者通常會適當增大核心筒的圍合面積占比。然而,由于框架才是使用者的主要活動場所,上述設計理念會因過分注重結構安全儲備而削弱了適用性和經(jīng)濟性。提升FCT結構經(jīng)濟性的直接途徑便是減小核心筒的圍合面積,但是該方法必然會削弱結構的抗震性能。根據(jù)結構布置宜采取多道防線的設計理念[4],可考慮在FCT結構中增設一道抗震防線以提高結構安全性能。近年來,部分研究者建議將FCT結構中的核心筒改設為若干子筒,通過構造措施將各子筒之間通過結構構件或者耗能裝置相連,使結構具備構件或者耗能裝置、子筒和框架三道抗震防線[5-6]。但該設計方法是將核心筒在原位置上進行拆分,并沒有真正實現(xiàn)筒體圍合面積的減小。借鑒分散筒結構體系的設計理念[7],本文建議可將傳統(tǒng)FCT結構體系的核心筒圍合面積進行縮小,同時在框架部分內均勻布置若干分布芯筒,形成框架-分布芯筒-核心筒(frame-distributed tubes-core tube,F(xiàn)DCT)新型高層結構體系。新體系的筒體總圍合面積要小于傳統(tǒng)FCT結構的核心筒圍合面積,其構體系示意圖如圖1(b)所示。FDCT結構形成了包括分布芯筒、核心筒及框架三道防線的三重抗側力體系,附加的分布芯筒對各子結構的抗震能力進行協(xié)調,而核心筒圍合面積的減小,可改善傳統(tǒng)FCT結構中核心筒剛度與框架相比懸殊較大在強震作用下出現(xiàn)過早屈服而對結構造成抗震不利的影響[8];各筒體總圍合面積占比的減小增加了結構的經(jīng)濟性,同時芯筒的分散布置也可提高結構布局的靈活性。
高層建筑在水平荷載作用下會發(fā)生側向位移并產(chǎn)生薄弱層破壞,由于FDCT結構的核心筒剛度相對較小,其薄弱層的破壞可能會更加嚴重。在結構中加入剛度較大的搖擺構件能有效地改變結構變形模式,抑制薄弱層的出現(xiàn),減小地震響應[9]。對結構附加搖擺構件的研究中,大多采用將框架結構與具有搖擺功能的剪力墻和填充墻等構件相結合的方式,相關研究表明附加搖擺構件可有效實現(xiàn)對框架結構的損傷控制,使其變形更加均勻,提高其抗震能力[10-12]。在搖擺體系與核心筒相結合方面,Meek[13]較早提出了搖擺核心筒結構,并采用簡化單自由度模型對不同高寬比的搖擺核心筒結構進行了分析。Nielsen等[14]對核心筒基礎固接與搖擺核心筒兩種形式進行了強震下性能對比分析,結果表明搖擺核心筒可以有效減小結構基底彎矩。
為了進一步提高框架-分布芯筒-核心筒結構體系抗震能力,控制結構損傷模式,提高結構變形均勻程度并減小薄弱層破壞,基于搖擺體系理念,本文認為可將具有足夠大剛度的分布芯筒與搖擺體系相結合,形成框架-分布搖擺芯筒-核心筒(frame-distributed rocking tubes-core tube,F(xiàn)DRCT)新型高層結構體系,該體系的示意圖如圖1(c)所示。本文將以FCT結構、FDCT結構和FDRCT結構為研究對象,以提高經(jīng)濟性為基礎分別設定三種結構的參數(shù),從力學機制出發(fā),建立各體系簡化分析模型,基于Lagrange方程和動量矩定理建立各體系運動方程,通過動力分析分別求解并對比不同結構的地震響應,之后對各個結構在不同場地以及不同類型長周期地震波下的抗震能力進行對比分析。最后,根據(jù)三種結構在不同類型地震波下性能-利潤總值的對比,驗證FDRCT結構在經(jīng)濟性和抗震減震能力兩方面同時具備優(yōu)勢。
1 FDCT結構體系運動方程
1.1 簡化分析模型
根據(jù)傳統(tǒng)FCT結構體系的構造形式以及工作原理可將其簡化為如圖2(a)所示的分析模型,其中結構中部的核心筒可簡化為一個底端固定的懸臂梁,將框架的每層等效為一個集中質量,核心筒和框架之間通過連梁進行剛性連接。
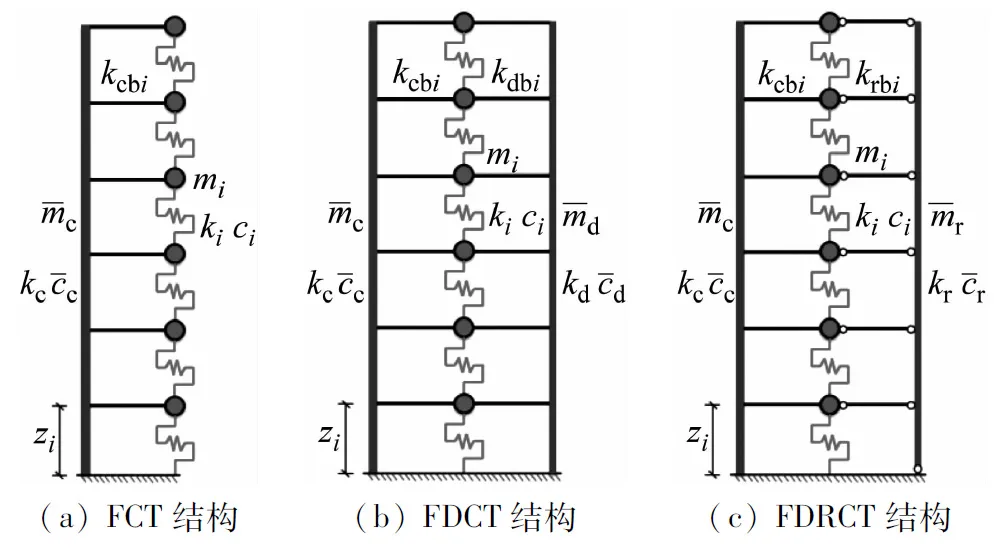
圖2 結構簡化分析模型Fig.2 The simplified analytical model of structure system
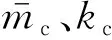
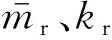
1.2 動力方程推導
考慮到以上高層結構體系受力復雜,在建立運動方程時結構的慣性力和彈性恢復力形式也較繁復,而Lagrange方程在運用過程中可不必直接分析上述因素,是完全的標量分析方法,因此本文運用Lagrange方程對以上三種結構體系進行運動方程的相關推導。由于FDRCT結構相對于FCT結構和FDCT結構工作機理較為復雜,其受力分析也最為全面,限于篇幅,本文僅闡述FDRCT結構的動力方程的推導過程,其它體系動力模型的建立方法是類似的。結構中的核心筒在簡化分析模型中被等效為一端固接的懸臂梁,因此,其筒體上任意一點z在t時刻相對于地面的水平位移為[15]
uc(z,t)=qc(t)φc(z)
(1)
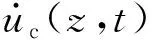
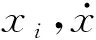
(2)
式中:T為結構體系的動能;V為結構體系的勢能;qi為結構體系中各子結構的廣義坐標,本文中qi包括qc、xi和θ,Qqi為對應廣義坐標qi的廣義力。
FDRCT結構體系的動能可表示為
(3)
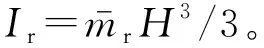
FDRCT結構體系的勢能為
(4)
式中,假設在實際工程中受到外部激勵的分布搖擺芯筒在搖擺過程中的轉角θ不會大于5°,因此其水平位移分量可用zisinθ進行計算。
FDRCT結構體系中存在非保守力做功,其包括地震慣性力以及阻尼力,設結構體系的虛位移為δqc,δxi,δθ,則地震力所做的虛功為
(5)
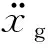
阻尼力作做的虛功為
(6)
根據(jù)式(5)和(6)得到廣義坐標qc、xi和θ所對應的廣義力Qqc,Qxi和Qθ,聯(lián)立式(3)和(4)并代入到(2),可得到FDRCT結構體系關于核心筒相對于地面水平位移的運動方程
(7)
由于分布搖擺芯筒轉角θ小于5°,在以下推導過程中將sinθ≈θ,cosθ≈1,關于框架中位移x1的運動方程為
(8)
關于框架中位移xi(i為2~n-1)的運動方程為:
[(ki+ki+1)+(kcbi+krbi)]xi-k1xi-1-
(9)
關于框架中位移xn的運動方程為
(10)
關于分布搖擺芯筒轉角的運動方程為
(11)
綜上,根據(jù)式(7)~(11)可得到FDRCT結構體系的質量矩陣、剛度矩陣、阻尼矩陣以及外荷載矩陣,進而推導出相應的狀態(tài)空間表達式,最終可采用Runge-Kutta方法實現(xiàn)方程組的時域求解及結構動力時程分析。
2 結構體系地震響應分析
2.1 結構信息
為了進一步研究FDCT結構體系和FDRCT結構體系相對于傳統(tǒng)FCT結構體系的抗震性能,本文設計了三種結構的分析模型并對其進行數(shù)值模擬。參考文獻[16]的結構模型,設計了一棟25層總高為100 m的FCT結構,其結構典型樓層示意圖如圖3(a)所示。在此結構基礎之上,將中部核心筒圍合面積進行相應縮小,并在核心筒與外圍框架對角連線中部分別布置了四個圍合面積較小的分布芯筒,形成FDCT結構,結構典型樓層示意圖如圖3(b)所示。FDRCT結構是在FDCT結構基礎之上將分布芯筒基底加入鉸接機制,同時與分布芯筒相連接的框架梁兩端也均需設置鉸接節(jié)點,使分布芯筒在地震作用下可發(fā)生充分的搖擺,其它結構信息均與FDCT結構相同。為了滿足FDRCT結構中搖擺體系的工程可行性,Qu等的搖擺墻齒狀鉸支座以及文獻[17]提出的彎曲耗能鉸,設計了分布搖擺芯筒基底所使用的雙向齒狀鉸支座和鉸接節(jié)點所使用的鉸接裝置,分別如圖4(a)和4(b)所示。雙向齒狀鉸支座通過剛性支撐與分布搖擺芯筒相連,支座下齒寬度大于上齒寬度,從而防止搖擺過程中發(fā)生脫落。上齒與下齒的咬合處均可做圓滑處理,確保搖擺功能的實現(xiàn)。在正常使用中梁端彎曲耗能鉸具有足夠的剛度,在地震時則可觸發(fā)鉸接機制,使梁端具備轉動能力。開孔軟鋼既可為梁端提供剛度,又可在地震時率先進入屈曲狀態(tài)并耗能。
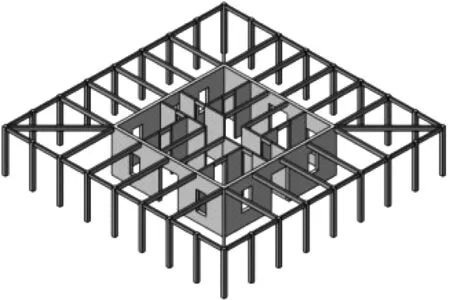
(a) FCT結構
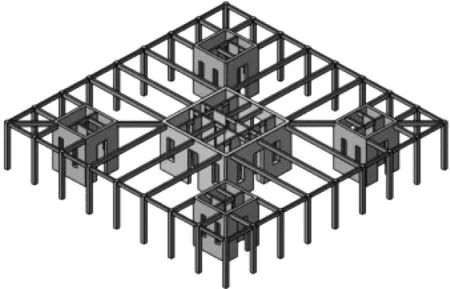
(b) FDCT結構圖3 結構典型樓層三維示意圖Fig.3 The 3D schematic diagram of the typical floor
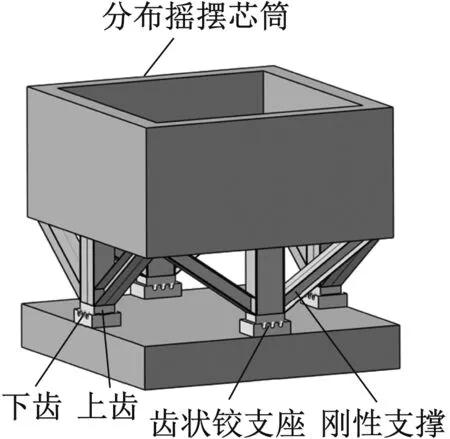
(a) 基底鉸接裝置

(b) 梁端鉸接裝置圖4 鉸接裝置構造圖Fig.4 Structural diagram of hinged devices
FCT結構模型與FDCT結構模型平面圖分別如圖5(a)及圖5(b)所示。結構共25層,總高為100 m,層高為4 m,結構平面尺寸為40 m×40 m。FCT結構的核心筒尺寸為20 m×20 m,其圍合面積占結構面積的25%;而為了提高結構經(jīng)濟性,將FDCT結構核心筒尺寸設為12 m×12 m,單個分布芯筒的尺寸為6 m×6 m,其筒體總圍合面積僅占結構總面積的18%。結構位于8度抗震設防區(qū),場地類別為Ⅲ類,設計地震分組為第1組。
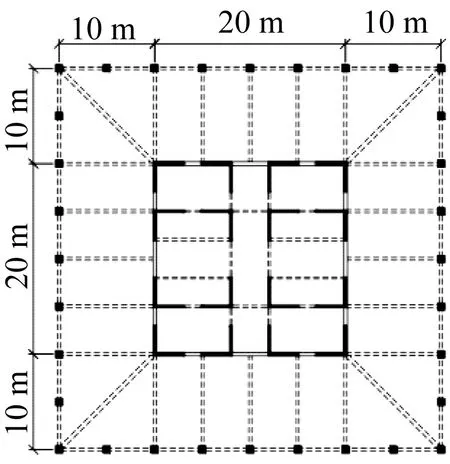
(a) FCT結構
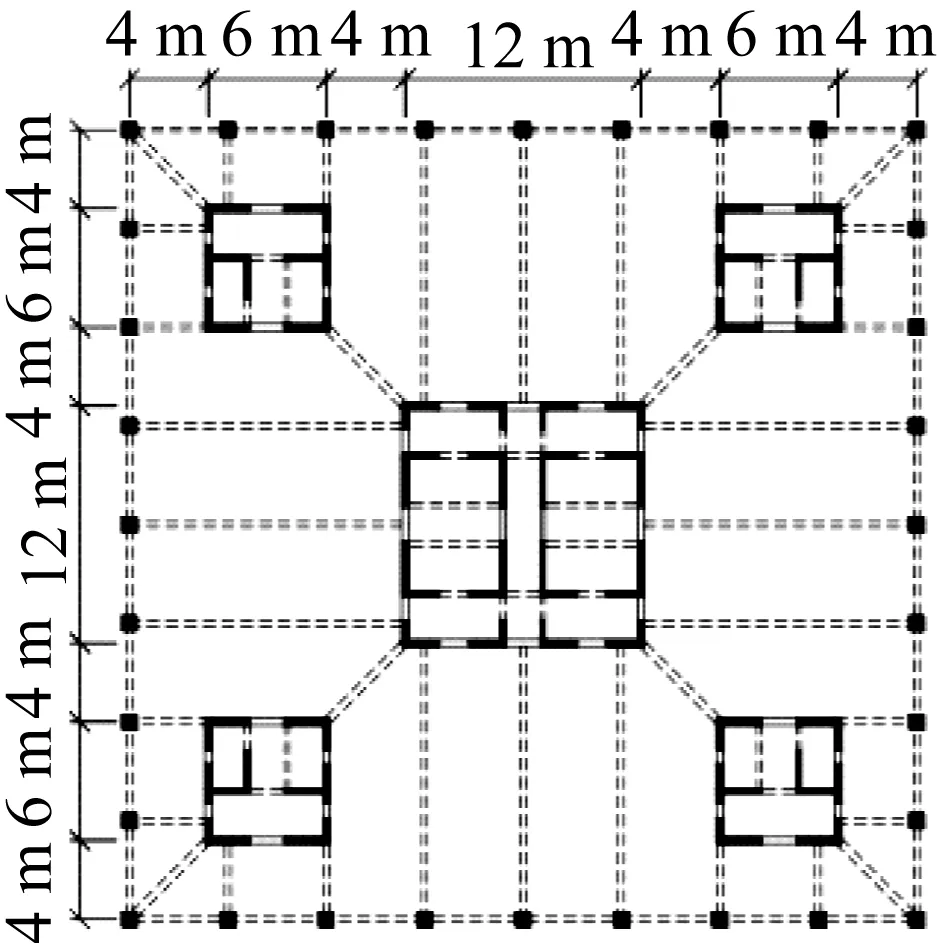
(b) FDCT結構圖5 結構平面圖Fig.5 Structural plan
FDCT結構和FDRCT結構的簡化分析模型參數(shù)需要在FCT結構基礎之上改設,其中FCT結構模型的主要構件信息為:圈梁為250×550 mm,角梁為400×850 mm,連系梁為300×700 mm,1~7層柱為750×750 mm,8~16層柱為700×700 mm,17~25層柱為600×600 mm,核心筒1~7層墻體厚度為500 mm,8~16層為450 mm,17~25層為400 mm,筒內墻厚度為250 mm,墻連梁為墻厚×1 200 mm,筒內梁為250×500 mm。
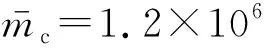
2.2 地震響應分析
本文共選取了三條實際地震波加速度記錄作為激勵,地震波具體信息如表1所示。由于結構在非線性狀態(tài)下的力學機理復雜,而上文所述理論分析以及數(shù)值模擬方法無法充分保證相關結果的準確性,因此本文僅探討結構在彈性狀態(tài)下的力學性能及減震效果。在此對FCT結構、FDCT結構和FDRCT結構進行動力時程分析時,將三條地震波的加速度峰值統(tǒng)一調為0.07 g(多遇地震)。
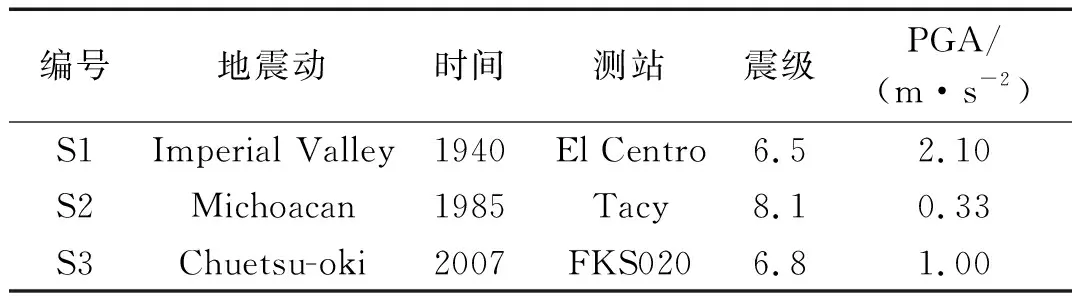
表1 地震動信息Tab.1 Information of ground motion
圖6為三種結構在不同地震波下結構頂層的位移時程,從圖中可以看出,相比于FCT結構,F(xiàn)DCT結構和FDRCT結構頂層位移會出現(xiàn)不同程度的增大。但相比于FDCT結構,F(xiàn)DRCT結構的位移有所減小,尤其是在峰值處的降幅更明顯,可見將搖擺體系加入到本文所提出的新型分散筒結構中是有助于控制結構位移響應的。

(a) S1
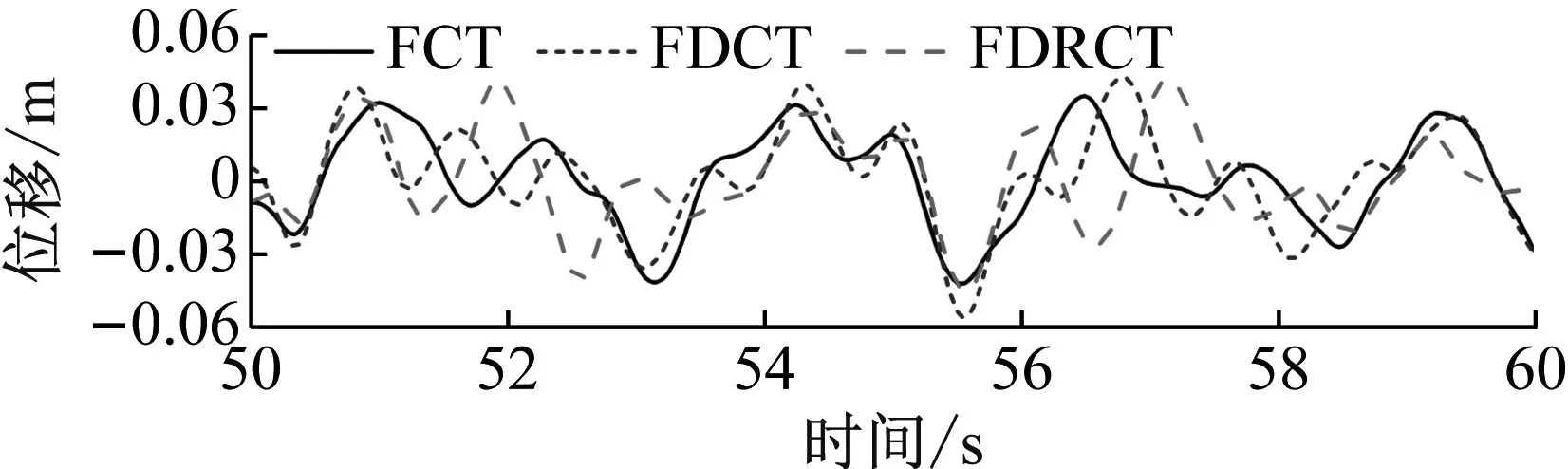
(b) S2
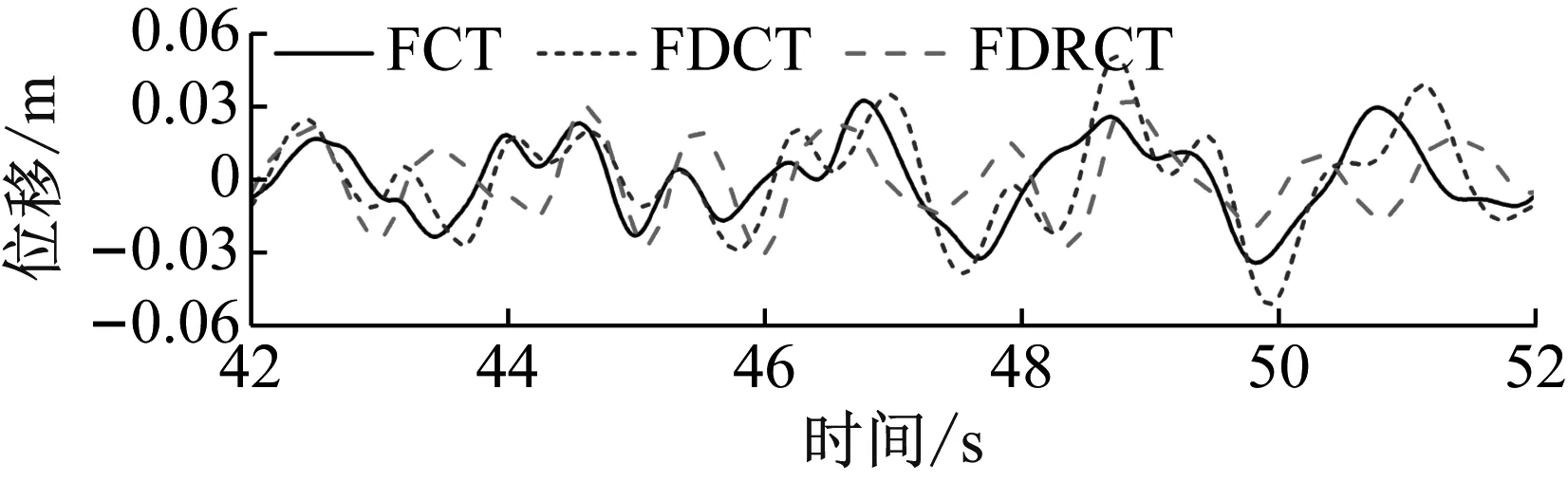
(c) S3圖6 地震下結構頂層位移時程Fig.6 Displacement time history curves of top story of structure subjected to earthquakes
圖7為三種結構在不同地震波下各層層間位移角對比,其中不同工況下結構的層間位移角均未超過規(guī)范要求的彈性狀態(tài)下的限值1/800,證明三種結構在合理的設計下均具有足夠的安全性能。可以看出:FDCT結構相對于FCT結構層間位移角呈現(xiàn)增大的情況,尤其是在結構中部樓層,層間位移角增大幅度更為明顯,這是由于FDCT結構筒體圍合面積的減小以及筒體進行了分散布置,結構剛度偏小,抗震能力偏弱,增加了薄弱層出現(xiàn)的幾率。然而,F(xiàn)DCT結構層間位移角并未超限,且考慮此新型結構體系對結構經(jīng)濟性的提升作用,可認為該結構方案具備基本的可行性。FDRCT結構相對于FDCT結構展現(xiàn)出了明顯的耗能減震優(yōu)勢,在三條地震波作用下其最大層間位移角分別減小了11.8%、27.1%和27.8%,且提高了結構變形的均勻程度。在S2波和S3波作用下,F(xiàn)DRCT結構大部分樓層層間位移角都接近FCT結構的結果,這表明相對于FDCT結構,F(xiàn)DRCT結構的動力響應顯著降低,結構具備較強的抗震及耗能減震能力。
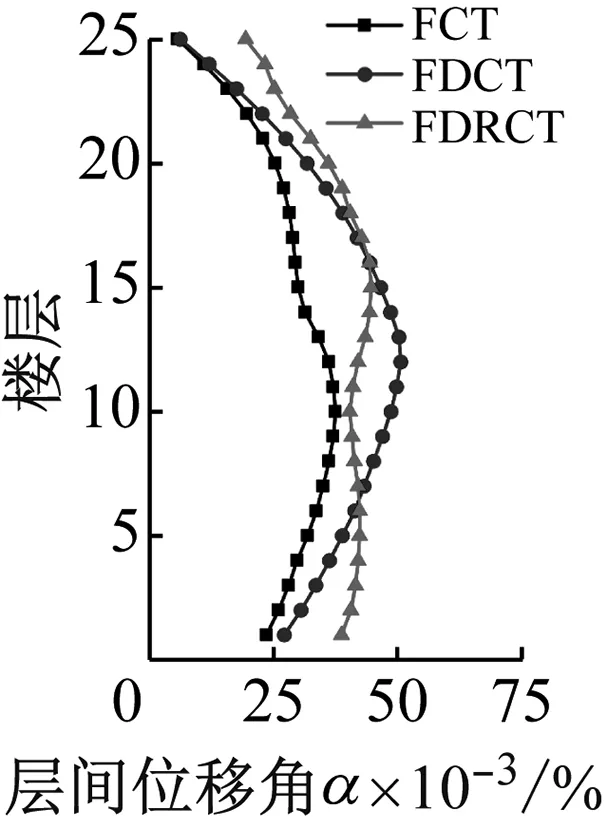
(a) S1
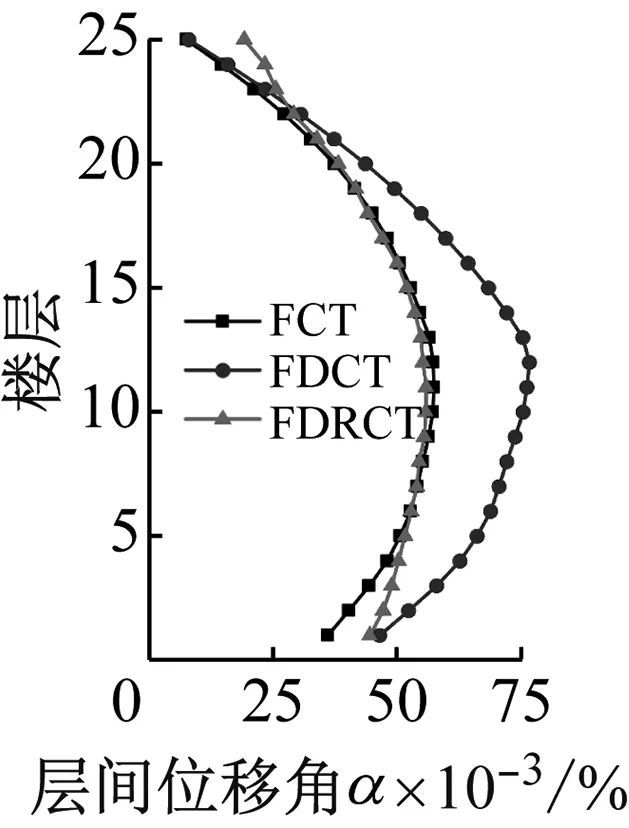
(b) S2
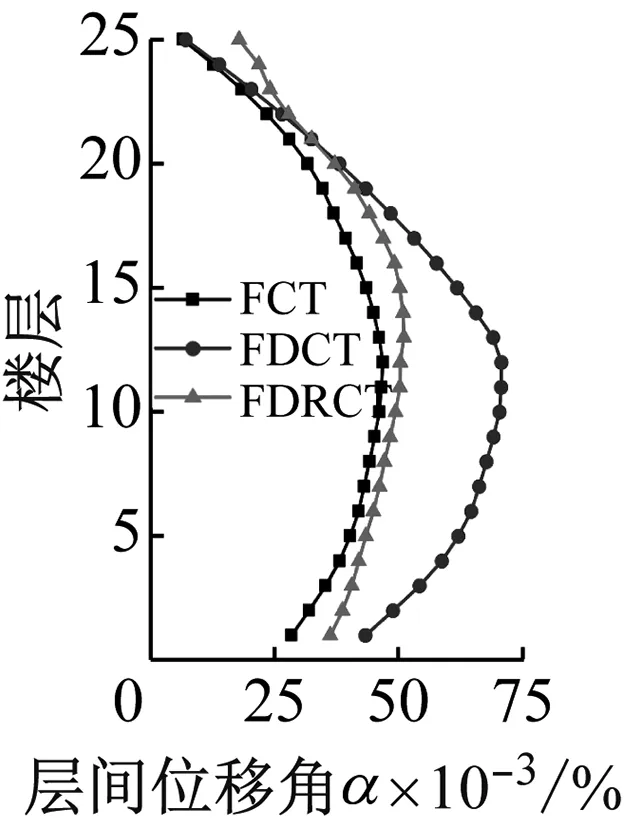
(c) S3圖7 地震下結構層間位移角Fig.7 Inter-story drift ratio of structures subjected to earthquakes
為了直觀評價三種結構各樓層層間變形的不均勻程度,并表征搖擺體系對結構變形和損傷的控制作用,可選用文獻[18]定義的層間位移集中系數(shù)(drift concentration factor, DCF)來進行對比,量綱歸一化指標DCF可按照下式計算,其數(shù)值越小表示結構樓層變形越均勻。
(12)
式中:αi為第i層的層間位移角;zi為第i層的層高;H為結構的總高度。
上述系數(shù)計算過程較復雜,宜提出一種機理明確且區(qū)分度更大的評價指標,參考統(tǒng)計學中變異系數(shù)的概念,本文認為可用結構各樓層的層間位移的變異系數(shù)(drift coefficient of variation, DCV)來評價不同結構各樓層層間變形的不均勻程度,其表達式如下,
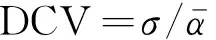
(13)
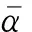
由式(12)和(13)計算得到的FCT結構、FDCT結構和FDRCT結構在不同地震波下的DCF和DCV如表2所示。從結果可知,相對于FCT結構,F(xiàn)DCT結構的數(shù)值都略有增大,而FDRCT結構的結果最小,這表明作為新增加的一道防線,分布搖擺芯筒能使結構變形更加均勻,有效控制結構的變形及損傷模式,最終提升了結構的抗震能力。對比三種結構的DCF和DCV,可以發(fā)現(xiàn)本文提出的DCV區(qū)分度更大,三種結構各樓層層間變形的不均勻程度可被明確區(qū)別,且DCV符合統(tǒng)計學原理,閾值合理且計算簡便,在評價各樓層層間變形的不均勻程度方面更具備優(yōu)勢。
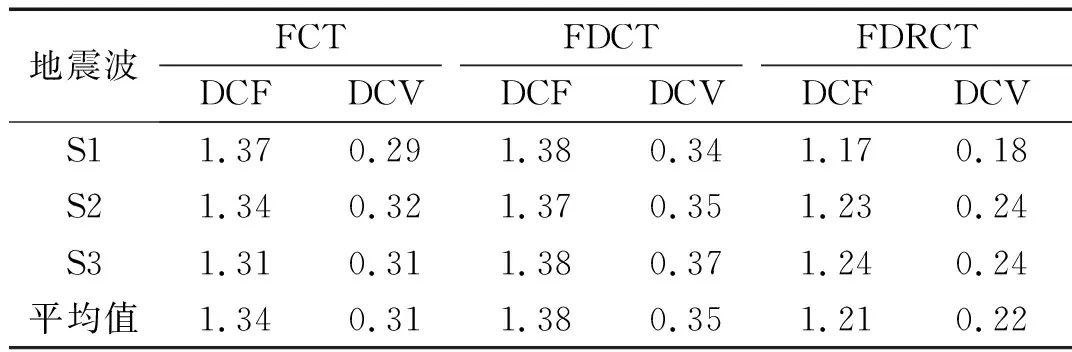
表2 不同結構DCF和DCV對比Tab.2 Comparison of different structural DCF and DCV
2.3 結構參數(shù)分析
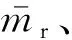
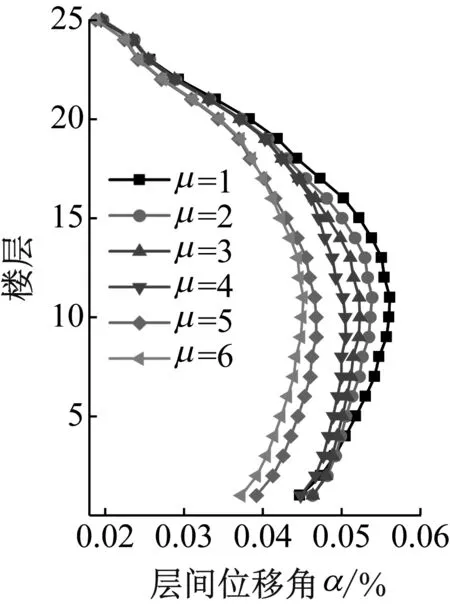
圖8 不同μ對層間位移角的影響Fig.8 Effect of different μ on the inter-story drift ratio
值得指出的是,由于FCT結構、FDCT結構和FDRCT結構的有限元模型較為復雜,基于精細化有限元模型進行動力分析和大量參數(shù)分析的計算效率較低,且本文所建立的力學方程和數(shù)值模擬分析可以基本反映結構的動力特性和抗震能力,并為實際工程設計提供初步指導,因此不再進行有限元模型層面的對比分析。
3 地震動特性對結構耗能減震性能影響
相關研究表明,結構在不同場地條件下的動力反應特性具有一定差異性,有必要對此進行對比分析。由于本文所研究對象為高層結構,而高層結構屬于長周期結構,在長周期地震動下此類結構的地震響應要遠大于普通地震動下的情況[19]。此外,長周期地震動又包括近場長周期地震動(近斷層脈沖型地震動) 和遠場長周期地震動(遠場諧和地震動),不同類型長周期地震動下高層結構的動力響應也會有差異[20]。有鑒于此,為了研究場地效應以及長周期地震動對FDRCT結構耗能減震性能的影響,本文參考文獻[21-22]的選波原則,針對四類場地分別選取了5條地震波,同時選取了5條近場長周期地震波和5條遠場長周期地震波,不同類型地震波加速度平均反應譜如圖9所示。各種類型地震波統(tǒng)一按照加速度峰值為0.07g(多遇地震)進行調幅。
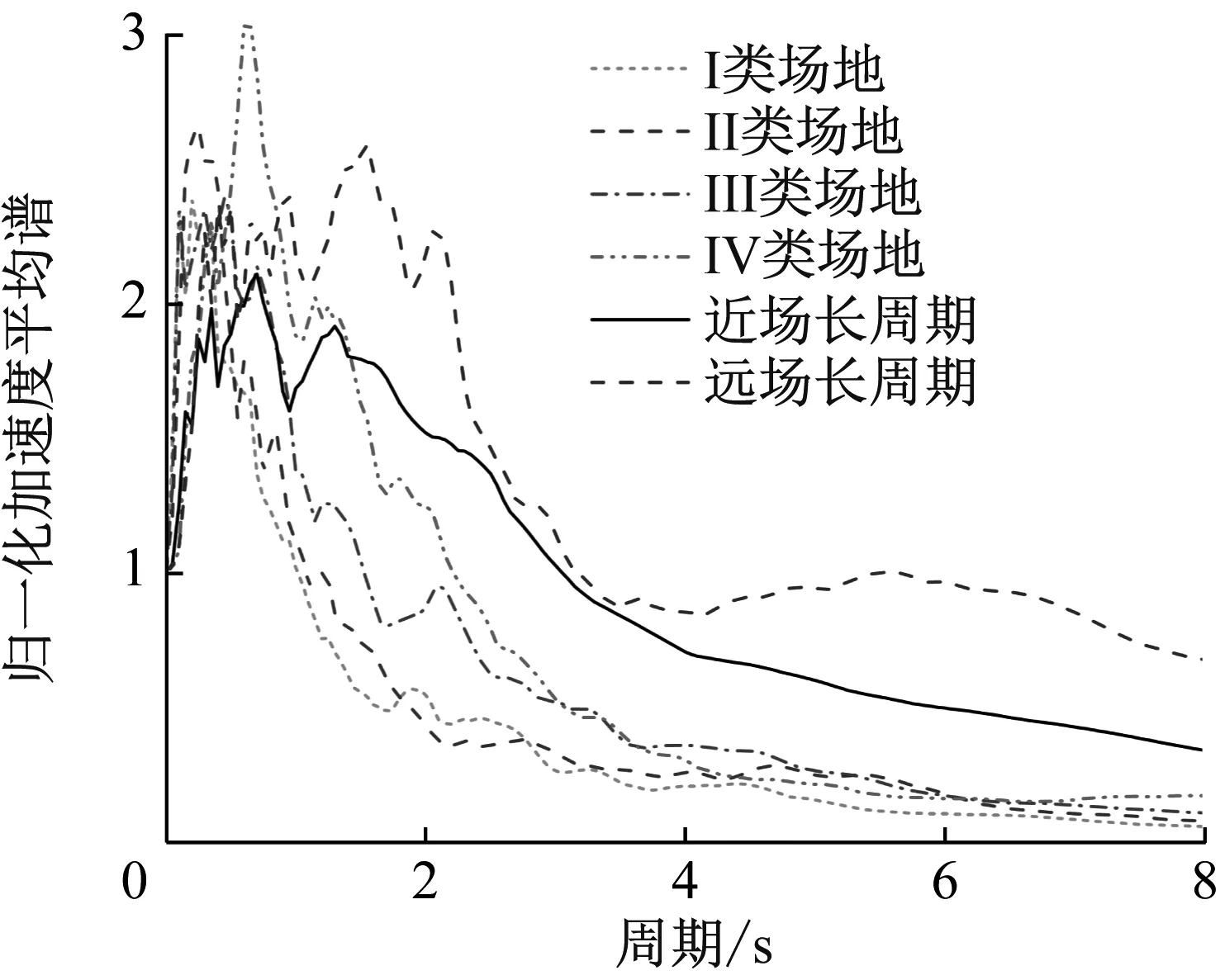
圖9 地震波加速度平均反應譜Fig.9 Acceleration average spectrum of seismic waves
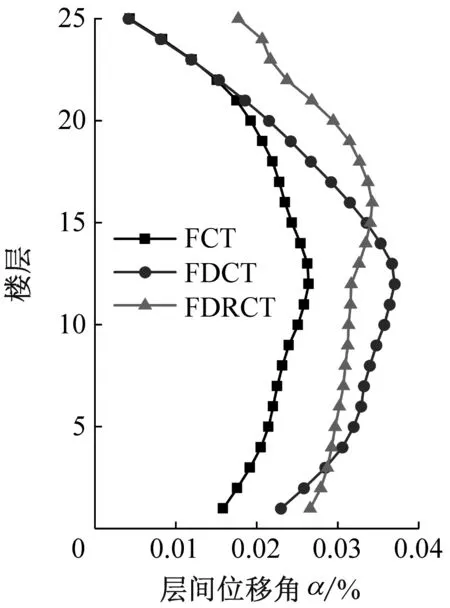
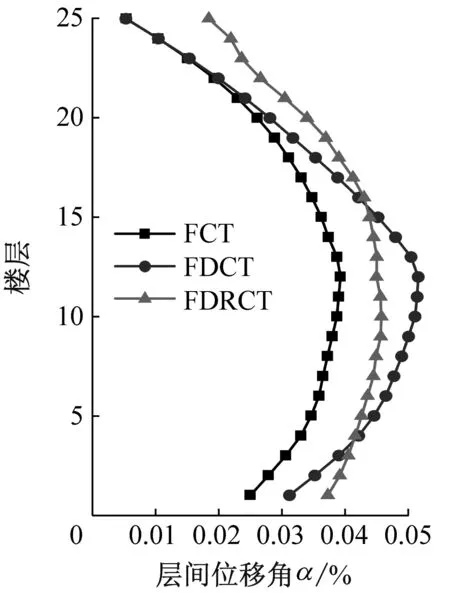
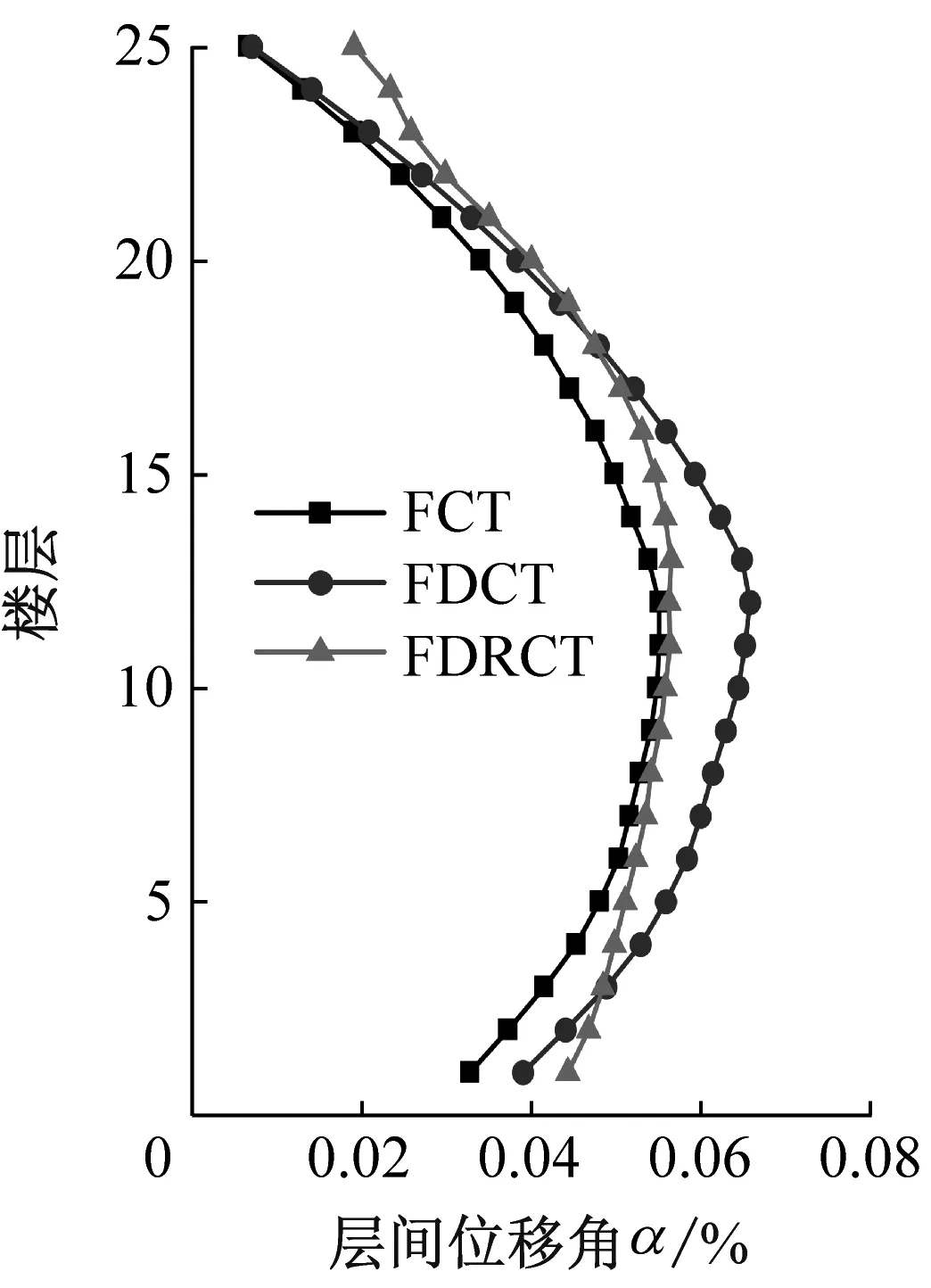
以上文分析中的FCT結構、FDCT結構和FDRCT結構模型為研究對象,對比分析不同類型地震波下三種結構的動力響應,探討FDRCT結構的抗震及耗能減震性能。圖10為FCT結構、FDCT結構和FDRCT結構在輸入不同類型地震波下的層間位移角均值曲線。對比圖10(a)~圖10(d)可知,從Ⅰ類場地至Ⅳ類,三種結構的動力反應依次增大。四類場地中,F(xiàn)DRCT結構最大層間位移角相對于FDCT結構均有所減小,在Ⅳ類場地中降幅最大,且此情況下FDRCT結構與FCT結構的層間位移角曲線已較為接近,說明在軟土地基中,具備搖擺功能的FDRCT結構擁有更優(yōu)的耗能減震能力。

(a) Ⅰ類場地
(b) Ⅱ類場地
(c) Ⅲ類場地
(d) Ⅳ類場地
(e) 近場長周期
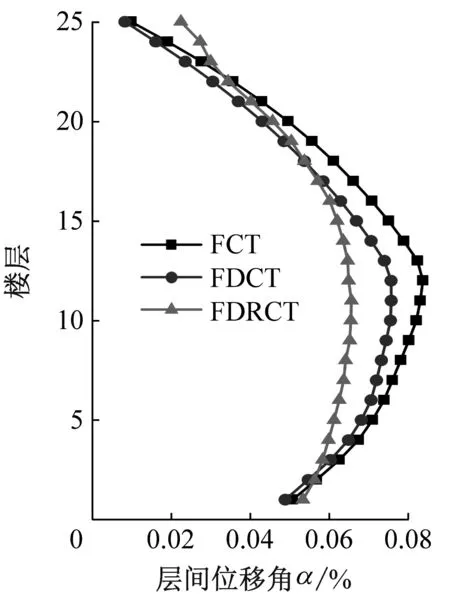
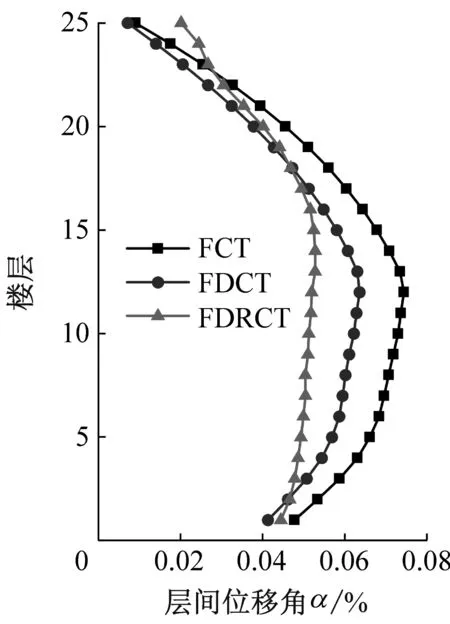
(f) 遠場長周期圖10 不同類型地震波下結構層間位移角對比Fig.10 Comparison of structural inter-story drift ratio under different types of seismic waves
由圖10(e)和圖10(f)可知,三種結構在長周期地震波下的動力響應顯著高于普通地震動的結果,且相對于近場長周期地震波,遠場長周期地震波對結構動力放大作用更為劇烈,這是主要是遠場長周期地震波的諧振效應對結構響應進一步放大造成的。此外,F(xiàn)DCT結構和FDRCT結構的最大層間位移角均要小于FCT結構,這說明不具備搖擺能力的FDCT結構在長周期地震動下也呈現(xiàn)出良好的抗震能力。相對于FDCT結構,F(xiàn)DRCT結構的最大層間位移角在輸入近場長周期地震波和遠場長周期地震波時分別減小了17.0%和13.3%,這表明在長周期地震動下具備搖擺功能的FDRCT結構具備突出的耗能減震效果,更適合抵御近場長周期地震波所產(chǎn)生的脈沖效應。
此外,由圖10中也可以看出:相比于FDCT結構,在不同類型地震波下,F(xiàn)DRCT結構的層間位移角曲線都呈現(xiàn)出了均勻的狀態(tài)。為了更為直觀的對比三種結構的不均勻程度,根據(jù)式(12)和式(13)分別計算出不同類型地震波下三種結構的DCF和DCV,結果如表3所示。
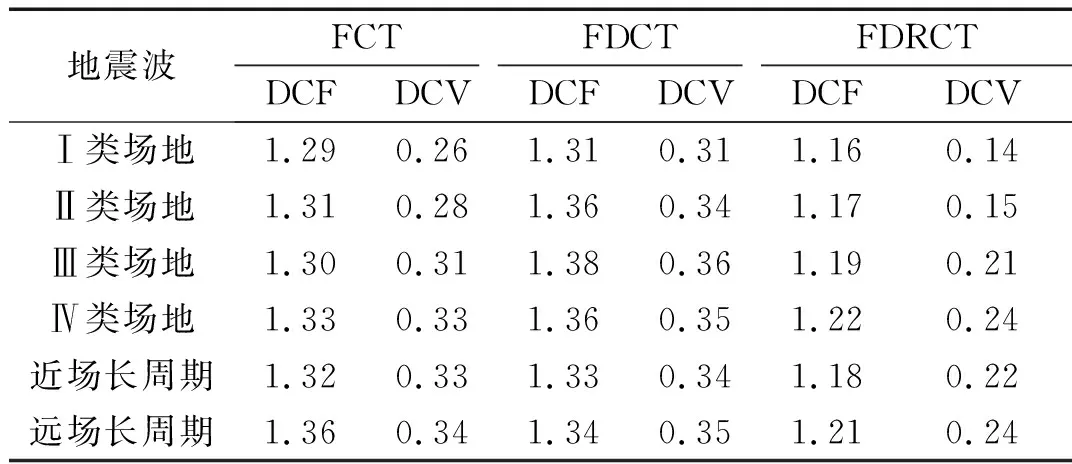
表3 不同地震波類型下結構的DCF和DCVTab.3 DCF and DCV under different types of seismic waves
從表3可看出,由于結構剛度的減小,F(xiàn)DCT結構相對于FCT結構其層間位移角不均勻性在不同類型地震波下會有不同程度增大,但在長周期地震波下,F(xiàn)CT結構和FDCT結構的DCF以及DCV十分接近,再次說明FDCT結構在抵御長周期地震波的可行性。三種結構中,F(xiàn)DRCT結構的DCF和DCV均為最小,層間變形最為均勻,再次證明附加搖擺體系的FDRCT結構能夠有效控制結構的變形模式,降低結構的動力響應。對比不同類型地震波周期下FDRCT結構的DCF和DCV,Ⅰ類場地和Ⅱ類場地均勻程度要大于Ⅲ類場地、Ⅳ類場地和長周期地震波,這是軟土場地和長周期地震波的頻譜較為豐富,受高層搖擺結構的高階振型的影響較大造成的,且本文提出的層間位移變異系數(shù)(DCV)更能凸顯此種效應。
4 基于性能-利潤總值的結構方案綜合評估
FDCT結構和FDRCT結構的設計理念是為了提高結構的經(jīng)濟性。為了進一步分析附加搖擺功能的FDRCT結構的經(jīng)濟性與抗震減震能力的優(yōu)勢,參考抗震減震結構性價比評估的概念,本文提出了基于結構抗震性能與利潤價格的評估指標,性能-利潤總值S的計算公式如下
S=a∑γiPi+bC
(14)
式中:Pi為抗震性能指標,其為新型結構與原結構的抗震性能參數(shù)之比。本文將FCT結構作為原結構,將FDCT結構或FDRCT結構作為新型結構。本文根據(jù)結構特色選取最大層間位移角、DCF或DCV兩種參數(shù)用以計算結構抗震性能指標。C為利潤指標,其為原結構與新型結構利潤值之比。a為抗震性能指標之和的權重系數(shù),b為利潤指標的權重系數(shù),γi為各個抗震性能指標Pi對應的權重系數(shù)。其中,Pi和C均為越大越好,因此,S越大表明新型結構方案越優(yōu)異。
為了對比DCF和本文所提出DCV作為結構性能-利潤總值中的抗震性能指標所得結果的差異性,共設定了兩種方案,第一種方案選取結構最大層間位移角以及DCF作為抗震性能指標,而第二種方案將DCF更換為DCV。本文追求的目標是提升結構經(jīng)濟性的同時保證結構的抗震性能,因此將式(13)中的權重系數(shù)a和b都設定為0.5,且本文對結構的抗震需求是在保證結構層間位移角盡可能減小的前提下再追求結構變形的均勻性,因此最大層間位移角所對應的P1的權重系數(shù)γ1設定為0.7,方案1中DCF和方案2中DCV所對應的P2的權重系數(shù)γ2設定為0.3。
本文研究的FCT結構、sFDCT結構和FDRCT結構三種模型的材料用量、成本和利潤如表4所示。計算結構成本時,鋼材單價取為5 000元/t,混凝土為500元/m3,梁鉸為2 000元/個,分布搖擺芯筒基底鉸支座100萬元/組。計算結構收益時,可根據(jù)三種結構的筒體圍合面積占比,計算得到FCT結構可出售的面積為30 000 m2,F(xiàn)DCT結構和FDRCT結構為32 800 m2,寫字樓綜合售價定為5萬元/m2,收益與成本之差即為結構的利潤。相比于FCT結構,F(xiàn)DCT結構和FDRCT結構利潤值分別提升了9.27%和8.25%,顯著提高了傳統(tǒng)FCT結構的經(jīng)濟性。
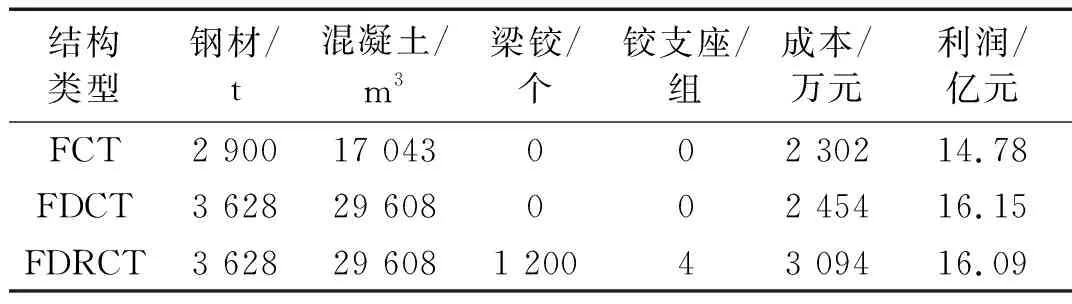
表4 結構材料用量、成本和收益對比Tab.4 Comparison of structural materials consumption, costs and benefits
三種結構的性能-利潤總值S結果如圖11所示。兩種方案計算所得的FDCT結構在不同類型地震波下的數(shù)值排序相同,而FDRCT結構的數(shù)值排序有所差別,這是由于方案2中的DCV更能突顯Ⅰ類場地和Ⅱ類場地由于均勻程度較大而有效提升結構S的情況,比較不同結構的S時區(qū)分度更大,這也證明了本文提出的層間位移變異系數(shù)效果更優(yōu)。在四類場地類別地震波下,相對于FCT結構,F(xiàn)DRCT結構的S都有不同程度的提高,而FDCT結構則都要小于FCT結構。在兩種長周期地震波下,F(xiàn)DCT結構和FDRCT結構的S都要高于FCT結構,且在近場長近場地震波下提升最為顯著,但整體對比分析而言,F(xiàn)DRCT結構的優(yōu)勢更為突出。由此可知,F(xiàn)DRCT結構具備兼顧經(jīng)濟性與安全性的優(yōu)勢,適宜在實際工程中推廣使用。
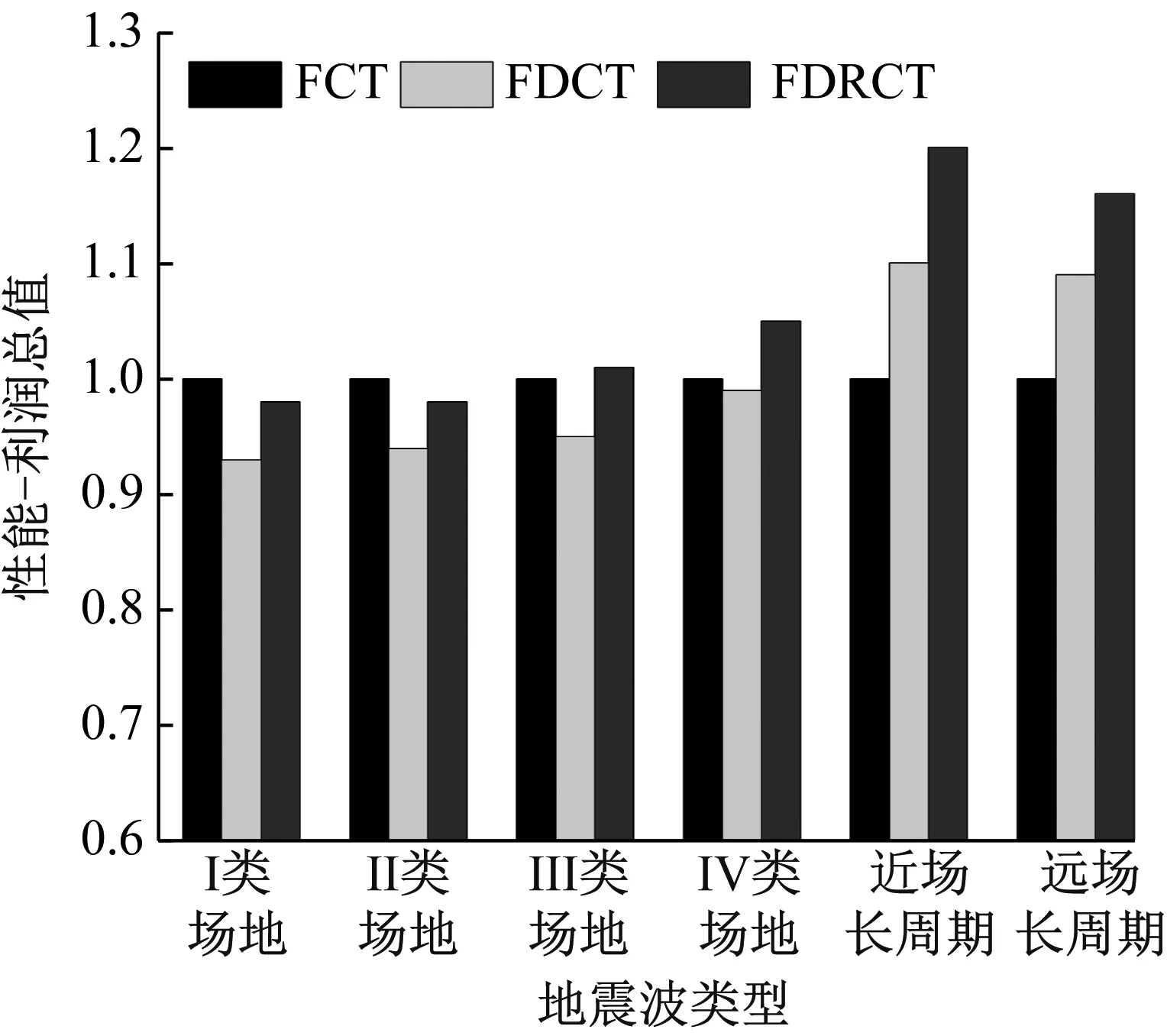
(a) 方案1
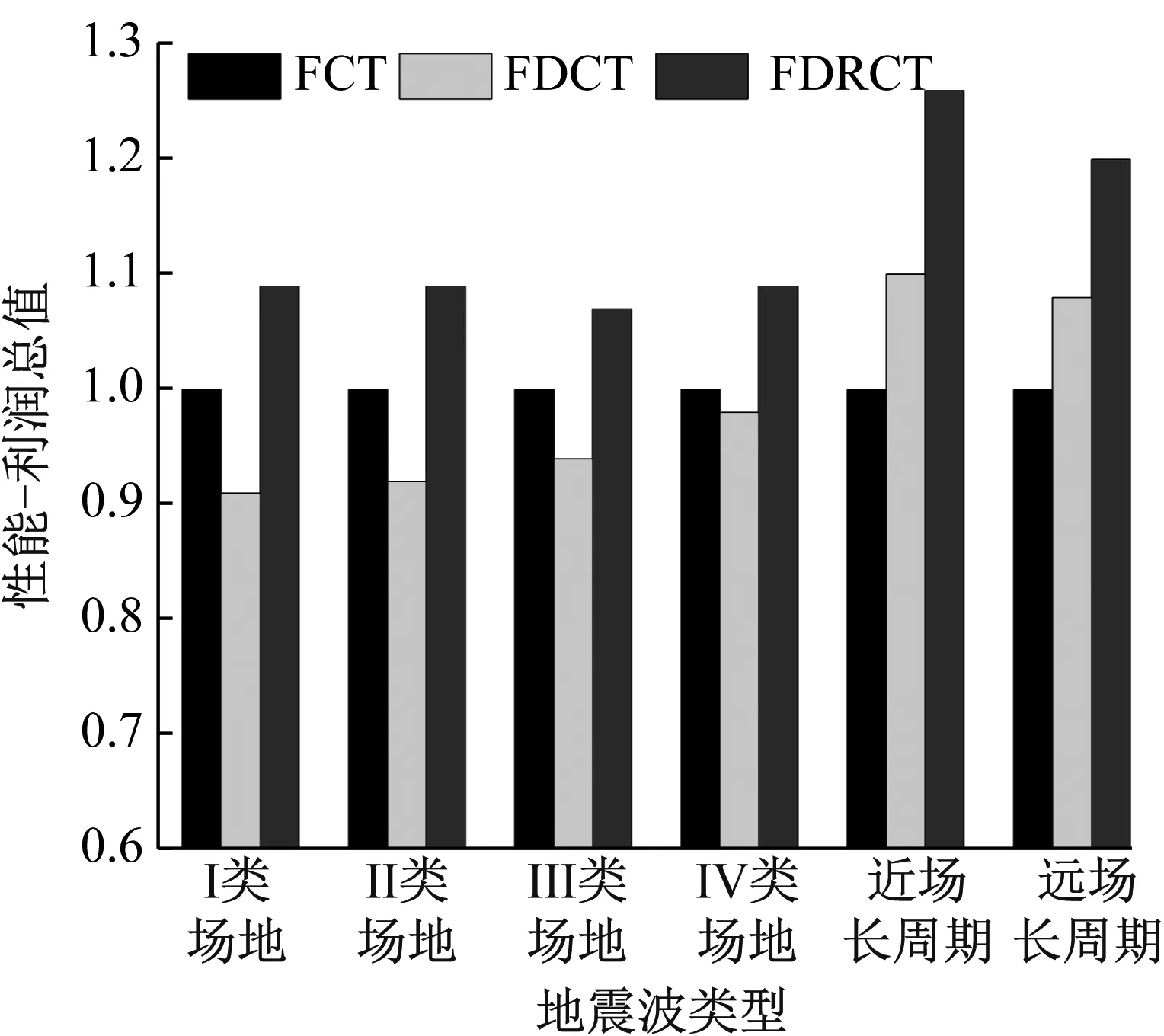
(b) 方案2圖11 不同結構性能-利潤總值S對比Fig.11 Comparison of different performance-profit values S
5 結 論
為了提升傳統(tǒng)FCT結構的經(jīng)濟性,本文提出了附加分布芯筒的FDCT新型結構體系,進而將搖擺體系與分布芯筒結合提出了FDRCT結構體系,以改善結構由于剛度下降造成的抗震能力削弱。基于Lagrange方程建立了三種結構的簡化動力模型,并進行了動力分析、場地效應和長周期地震波影響分析以及性能-利潤總值評估,結論如下:
(1) 根據(jù)FCT結構、FDCT結構和FDRCT結構簡化分析模型,基于Lagrange方程推導了相應的動力方程,并根據(jù)結構動力時程分析驗證了該理論的可行性。地震作用下FDCT結構的動力響應相對較大,抗震能力有所下降。FDRCT結構頂層位移和最大層間位移角都要小于FDCT結構,對比三種結構的DCF和DCV結果,F(xiàn)DRCT結構的層間變形最為均勻,表明搖擺體系可以對本文中的分散筒結構有較好的控制效果,本文提出的DCV參數(shù)可以更準確便捷地評價樓層不均勻性。此外,由FDRCT結構地震作用下參數(shù)分析可知,增大分布搖擺芯筒的質量,可提高FDRCT結構的耗能減震能力。
(2) 對三種結構進行了不同場地類別以及不同類型長周期地震波下動力分析,結果表明遠場諧和地震波對結構造成的累積破壞最為嚴重。在不同地震波類型下,F(xiàn)DRCT結構的動力響應結果都要小于FDCT結構,且DCF以及DCV皆為最小,證明了FDRCT結構因優(yōu)越的耗能減震性能而具備廣泛的適用性。相對于FCT結構,F(xiàn)DCT結構和FDRCT結構更有利于抵御長周期地震波的破壞,但FDRCT結構效果更為突出。
(3) FDCT結構和FDRCT結構相對于FCT結構的利潤值分別提升了9.27%和8.25%。基于性能-利潤總值的結構綜合評估結果表明,F(xiàn)DRCT結構在不同類型地震波下其性能-利潤總值都要優(yōu)于FCT結構,尤其是在長周期地震波下提高幅度更大。FDRCT結構不僅可以提升結構的經(jīng)濟性,同時兼顧了結構的安全性,具備良好的推廣應用價值。

