載瘤動脈雙向流固耦合動力學數值模擬分析

王得辰， 張俊婷， 樊佳偉

(太原科技大學 應用科學學院， 山西 太原 030024)

0 引 言

動脈瘤是由于動脈壁的病變或損傷而出現的動脈壁局限性或彌漫性擴張或膨出， 這類疾病有著較高的發病率及死亡率。 研究表明， 動脈瘤的生長、 破裂與動脈血流特征有關[1]。 相關研究表明[2-12]， 血流動力學因素的異常改變是動脈瘤破裂的重要因素之一， 在相同的動力學模型下， 血流動力學不僅與動脈瘤的形狀、 大小、 位置、 動脈瘤頸口大小等有關， 也與載瘤動脈的直徑、 瘤壁厚、 彎曲度及彈性模量等有關。 人體內的血管外部被組織液所包圍， 這些液體會對血管外壁產生外壓力， 最終可能會導致實驗模擬計算的數值小于實際值[6]。 因此， 本文對載瘤動脈的彎曲度、 動脈瘤高等與動脈血流動力學特征的關系進行有限元數值模擬和探討， 旨在發現線彈性條件下影響動脈瘤破裂的血流動力學因素， 為臨床提供參考。

1 動脈載瘤模型的建立

1.1 雙向流固耦合力學模型

血液在血管中流動的流動方程可用Navier-Stokes方程[13]來描述。

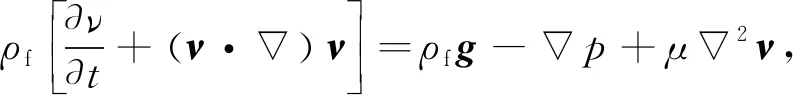
(1)

式中：ρf為血液密度；t為時間；ν為速度矢量；g為重力加速度矢量；p為壓力；μ為黏性參數。

動脈瘤組織控制方程為

ρsas=·σs,

(2)

式中：ρs為動脈管壁密度；as為管壁質點加速度；σs為血管及血管瘤的應力張量。

血液在血管中流動還要滿足連續性方程， 對于不可壓縮流體可表示為

·ν=0.

(3)

在流固耦合交界面上， 變量的傳遞方程[14]應滿足

ds=df,

(4)

τs·ns=τf·nf,

(5)

μs=μf,

(6)

式中：ds為固體的位移；df為流體的位移；τs為血管及血管瘤的剪切力矢量；……