儲能系統中三電平圖騰柱AC-DC變換器的研究

敬 成，王 袁，徐 兵

(1.三峽大學電氣與新能源學院，湖北 宜昌 443002；2. 上海電力大學自動化工程學院，上海 200090；3.遼寧東科電力有限公司，遼寧 沈陽 110179)

以光伏(photovoltaic，PV)、風電、電動汽車(electric vehicle，EV)為代表的新能源行業對“雙碳”實現起強大推進作用[1-4]。但大量新能源發電并網對電網穩定性產生影響，限制了新能源發展，因此為保證電能質量儲能系統孕育而生[5-8]。

圖1為常用的儲能系統結構，由AC-DC變換器和DC-DC變換器組成。其中，AC-DC變換器作為儲能系統核心部分，國內外學者對其進行了大量研究[9-12]。在眾多AC-DC變換器中，多電平變換器具有諧波含量少、電壓電流應力小、功率密度及效率高等優勢，正逐步取代兩電平變換器[13-15]。

文獻[16-18]從控制和拓撲結構方面對三電平電路開展研究。文獻[16]采用傳統三電平AC-DC變換器對模型預測控制改進，解決了低頻控制精度差的問題，但電路拓撲采用大量開關器件，電路成本及損耗較高。文獻[17]中拓撲一定程度上減少了開關管數目，并且電路能實現雙向功率流動，但電路在器件總數上還能進一步優化。文獻[18]提出了一種T型三電平變換器，該變換器在開關管數目與文獻[17]一致的情況下，減少了2個二極管的使用，電路成本上得到控制，但缺少拓撲推衍過程。

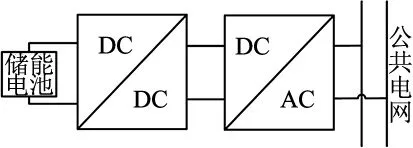
圖1 儲能系統常用結構

基于上述分析，在三電平橋臂變形后對各個器件重新連接，推衍出新型三電平橋臂。將所推橋臂與兩電平圖騰柱無橋電路級聯，提出一族新型三電平電路。所提電路結合無橋電路和三電平電路優勢，且成本較低，能應用于儲能系統。同時，此類方法在對兩電平電路優化為三電平電路以及三電平電路本身的優化具有通用性，應用場景較廣。

1 拓撲推衍及原理分析

1.1 拓撲推衍

本文以T型三電平拓撲為基礎，對T型三電平橋臂變形，推衍出新型三電平橋臂。圖2為2種常用T型三電平橋臂，圖2(a)通常用于功率單向流動場景中，圖2(b)通常用于功率雙向流動場景中。

基于圖2所示2種常用T型三電平橋臂，推衍出新型三電平橋臂，如圖3所示。為便于分析，在橋臂下方編號，如A1、A2。如圖3(a)，在A1上2個二極管支路上串聯開關管，得到A2*，去除A2*上開關管S2、S3后用實線重新連接，得到A2。同理，將B1的2個開關管支路串聯開關管得到B2*，再去掉冗余開關管后重新連接得到B2。

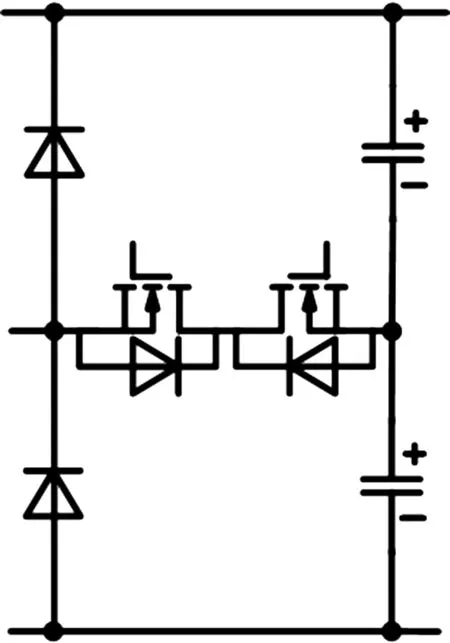
(a)單向三電平橋臂

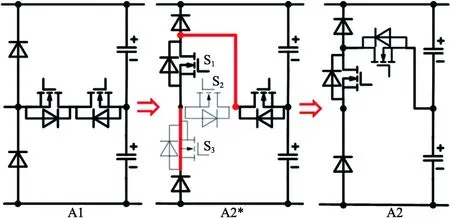
(a)單向三電平橋臂

基于上述橋臂變換，將新橋臂A2、B2與圖騰柱橋臂級聯，提出一族三電平圖騰柱AC-DC變換器，如圖4所示。按照功率流動特點，圖4(a)所示電路命名為單向三電平圖騰柱AC-DC變換器(unidirectional three-level totem-pole AC-DC converter，UTPC)，圖4(b)所示電路命名為雙向三電平圖騰柱AC-DC變換器(bidirectional three-level totem-pole AC-DC converter，BTPC)。

1.2 原理分析

為驗證所提一族三電平圖騰柱AC-DC變換器有效性，本文以UTPC為例進行工作原理分析。1個周期內，UTPC有6種工作模式，如圖5所示。為便于分析，假定電感L足夠大，變換器工作在連續導通模式(continuous conduction mode，CCM)；電容C1、C2大小相等，直流電壓Udc恒定。

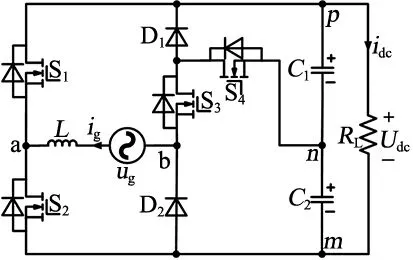
(a)單向三電平圖騰柱AC-DC變換器

模式1：電網電壓ug>0，a節點與b節點間電壓uab=0。S2、D2導通，電容C1、C2向負載放電，如圖5(a)所示。

模式2：ug>0，uab=0.5Udc。S3導通，S1、S4體二極管導通，C1充電、C2向負載放電，如圖5(b)所示。

模式3：ug>0，uab=Udc。S1體二極管導通，D2導通，C1、C2充電，交流電源直接向負載供電，如圖5(c)所示。

模式4：ug<0，uab=0。S1、S3、D1導通，C1、C2向負載放電，如圖5(d)所示。

模式5：ug<0，uab=-0.5Udc。S4導通，S2、S3體二極管導通，C2充電、C1向負載放電，如圖5(e)所示。

模式6：ug<0，uab=Udc。S2、S3體二極管導通， D1導通，C1、C2充電，交流電源直接向負載供電，如圖5(f)所示。

基于上述分析，表1總結出UTPC的開關狀態表，表中“0”、“1”分別表示開關管開與關，“↑”表示電容充電，“↓”表示電容放電。

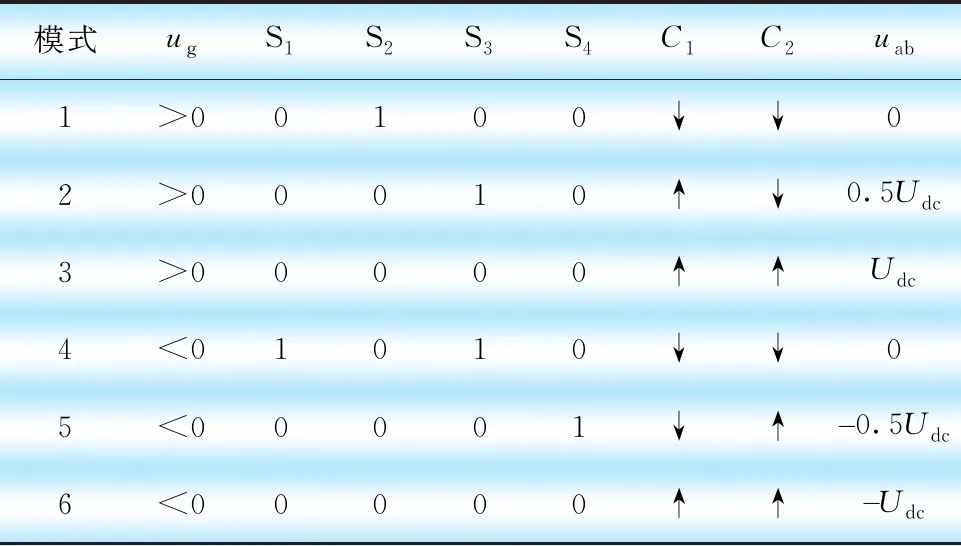
表1 UTPC開關狀態表

1.3 現有拓撲對比

表2為本文提出拓撲與現有多電平拓撲有源器件數目對比。對比可知，UTPC使用開關管最少，便于實現控制和調制。文獻[18]中拓撲與BTPC均能實現功率雙向流動，且器件使用相對最少。因此，本文所提拓撲在成本和效率上具有一定優勢。

表2 所提拓撲與現有拓撲有源器件數目對比

2 控制與調制方案

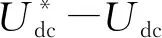
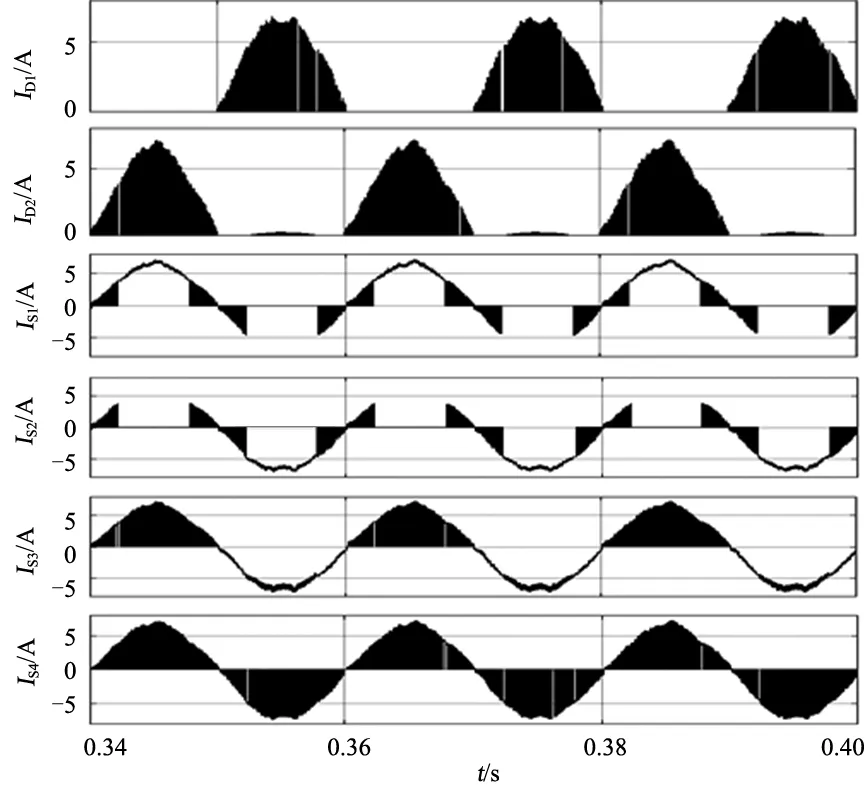
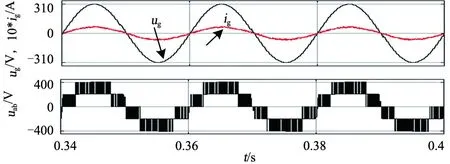
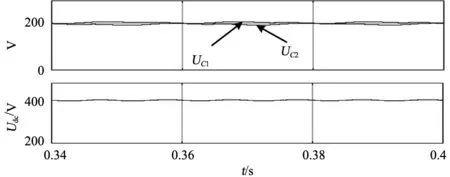
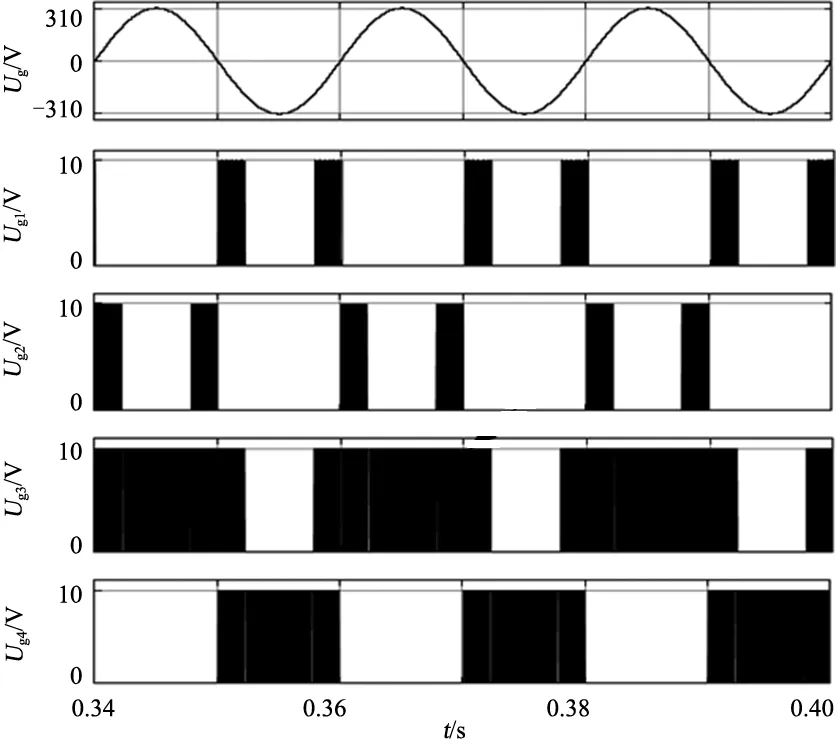
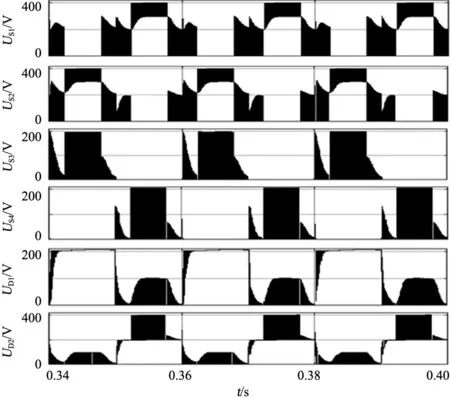
將參考信號vref(控制輸出電壓)與載波信號比較，得到UTPC開關脈沖信號，如圖6下半部分所示。在正半周期，當0<0.5vref< 1時，電路在模式3與2間交替工作；當0

基于上述調制分析，結合6種工作模式，根據式(1)—(6)可表示出該調制下正半周期占空比表達式，式中Ug,max為電網電壓幅值，Ton、Toff分別為開關管導通和關斷時間。

圖6 控制與調制方案

定義調制比M為

M=Ug,max/Udc

(1)

占空比Q為

Q=Ton/(Ton+Toff)

(2)

ug·Ton=(0.5Udc-ug)·Toff

(3)

(ug-0.5Udc)·Ton=(Udc-ug)·Toff

(4)

將式(3)、(4)分別代入式(1)、(2)得2種情況下占空比Q1、Q2為

Q1=1-2Msin(wt)

(5)

Q2=1-2Msin(wt)

(6)

3 性能分析

3.1 電壓應力分析

由1.3節幾種拓撲對比可知，文獻[18]與本文所提拓撲器件數目類似，故對文獻[18]中拓撲與本文所提拓撲進一步對比電壓應力。基于圖5所示工作模式分析，總結出3種電路電壓應力，如表3所示。由表3可知，文獻[18]中拓撲只有2個器件電壓應力減半，而本文提出2種拓撲均有3個器件電壓應力減半，即本文提出電路在成本上更具優勢。

表3 3種電路最大電壓應力對比

3.2 電流應力分析

為了估計器件損耗，需要計算流過器件電流平均值和有效值。本文以UTPC為例，對其有源器件電流應力分析。圖7為UTPC在Matlab/Simulink環境下電流應力仿真波形，結合電路工作模式和調制分析，各器件電流應力可由式(7)—(16)表示。其中僅二極管D1、D2電流應力給出計算過程，其余器件與之類似，故不再詳細推導。

二極管D1、D2電流有效值為

(7)

圖7 UTPC電流應力仿真波形

將式(5)、(6)代入式(7)，得：

(8)

二極管D1、D2電流平均值為

(9)

將式(5)、(6)代入式(9)，得：

(10)

開關管S1、S2電流有效值為

(11)

開關管S1、S2電流平均值為

(12)

開關管S3電流有效值為

(13)

開關管S3電流平均值為

(14)

開關管S4電流有效值為

(15)

開關管S4電流平均值為

(16)

表4為UTPC中有源器件在功率等級為1 kW時電流應力計算值與仿真值對比。其中，計算值取Ig,max=6.75 A。由表4可知，UTPC中有源器件電流應力計算值與仿真值結果誤差均不超過5%，驗證了上述公式的正確性。

表4 電流應力計算值與仿真值對比

4 仿真分析

搭建UTPC的Matlab/Simulink仿真模型，仿真參數如表5所示。

表5 仿真參數

圖8為輸入及輸出側波形，圖8(a)為交流側輸入波形，電流ig與電壓ug同相位，且曲線光滑；橋臂電壓uab有5個階梯，符合三電平電路特點。圖8(b)為直流側輸出波形，2個電容電壓均在200 V上下波動，電容電壓動態平衡；直流輸出波形恒定，達到預期效果。

(a)交流電壓電流及橋臂電壓uab波形

(b)直流電容電壓及直流輸出電壓波形

圖9 開關脈沖分配波形

圖9為UTPC開關脈沖波形，與圖5和圖6理論分析吻合。圖10為有源器件電壓應力波形，與表3最大電壓應力一致。

圖10 有源器件電壓應力波形

5 結語

本文基于T型三電平橋臂，推衍出一族新型三電平AC-DC變換器。從原理分析、控制與調制策略和性能分析方面，對本文提出電路進行理論分析。由分析可知，UTPC適用于單向功率流動場景，相對于其他三電平拓撲開關器件較少，成本最低；BTPC 適用于雙向功率流動場景在雙向AC-DC變換器中電路成本也具備一定優勢。最后，通過仿真分析，證實了所提電路良好的穩態性能，在儲能系統、電動汽車充電系統中具有一定應用價值。