考慮瀝青混合料空隙率的蠕變特性及改進Burgers模型

肖敏敏, 程韋*, 楊禮明

(1.上海應用技術大學城市建設與安全工程學院，上海 201418；2.廣西交通設計集團有限公司，南寧 530029)

隨著道路交通流量的迅速增加，路面所承受的汽車軸載也隨之提高，導致路面大面積出現病害。其中，由于瀝青抗變形能力不足導致的瀝青路面出現車轍、擁包等問題頻頻出現。為了延長路面的使用壽命，減少路面變形類病害發生的幾率，瀝青混合料的抗變形能力已然成為瀝青路面研究的重點和道路研究者重點關注的問題[1-3]。

目前對瀝青混合料的抗變形能力的研究主要通過室內蠕變試驗，通過在特定溫度下，在圓柱形試件上施加恒定荷載，進而測定瀝青混合料變形隨時間的變化規律[4-5]。一般情況下，瀝青混合料剛度越大，蠕變變形越小，混合料抵抗變形的能力越強，反之，瀝青混合料的柔度越大，蠕變變形越大，混合料抵抗變形的能力越差。張啟鵬等[6]對AC-13瀝青混合料進行了不同應力水平下的單軸壓縮蠕變試驗，確定了不同應力水平下分數階蠕變損傷模型的參數與損傷演化曲線。Xzabc等[7]為了研究玄武巖纖維(BF)增強瀝青混凝土的黏彈性蠕變特性，在0和0.3%BF含量下，分別對AC13和AC20兩種瀝青混凝土進行了SCB(circular bending test)蠕變試驗，發現增加纖維含量有利于增強瀝青混凝土的抗變形能力。Azarhoosh等[8]采用苯乙烯-乙烯/丙烯-苯乙烯(SEPS)納米復合材料用作瀝青結合料改性劑，通過多重應力蠕變試驗評估瀝青結合料的蠕變性能，實驗結果表明，改性瀝青黏合劑對瀝青混合料永久變形的影響較小。Yazdipanah等[9]通過動態蠕變試驗研究有機WMA(warm mix asphalt)添加劑松散蠟(SW)對橡膠瀝青混合料蠕變性能的影響，發現瀝青混合料產生了更能抵抗蠕變變形的混合物，從而提高了抵抗變形的能力。Jahangiri等[10]在0、-12、-24 ℃下使用蠕變試驗來確定瀝青混凝土低溫蠕變性能，提出了一種評價瀝青混凝土抗變形能力的新思路。學者們通過室內蠕變試驗研究瀝青混合料的蠕變特性，試驗所得到的結果直觀可靠。而部分學者通過對瀝青混合料的黏彈性本構模型進行定義，通過科學計算分析瀝青混合料的蠕變特性，可以達到節省時間以及資源的目的。其中，Burgers模型作為瀝青混合料常用的黏彈性本構模型，對于一般的瀝青混合料的黏彈性表達效果較好，學者們將其作為瀝青混合料的本構模型開展了對于瀝青混合料的一系列研究工作。

Xue等[11]采用線接觸模型和Burger接觸模型分別用于表征粗集料和瀝青膠漿的力學性能，分析了瀝青混合料在車轍發展過程中的微觀力學響應，研究表明，Burger接觸模型作為瀝青混合料的本構模型可以有效地預測瀝青混合料的變形的規律。Wang等[12]采用Burgers模型定義瀝青混合料的黏彈性，采用二維離散元法DEM(discrete element method)隨機生成形狀不規則的聚集顆粒，對瀝青混合料進行虛擬動態蠕變試驗，有效模擬了動態蠕變試驗，其相對誤差一般小于10%，且虛擬試驗結果符合室內試驗規律。宋長振等[13]將被壓瀝青混合料本構模型簡化為Burgers模型，建立了振動壓路機與被壓材料耦合的二自由度振動模型，分析了被壓材料參數對振動輪振動加速度幅值的影響規律，得出了振動輪加速度幅值與空隙率、溫度之間的變化關系。You等[14-15]通過采用三軸蠕變試驗測試了不同瀝青混合料在100、300、500 kPa應力水平下的蠕變，采用Burgers 模型對試驗結果進行擬合，每個應力水平上的擬合效果相關性都大于 0.98，能很好地描述瀝青砂漿在重復荷載作用下的蠕變特性。Zhang等[16]基于瀝青混合料動態模量的極值特性和線性黏彈性力學理論，確定了瀝青混合料Burgers模型的參數，通過Burgers模型結合室內試驗分析了瀝青混合料的蠕變效應。

上述研究表明，Burgers模型可以較好地表征瀝青混合料的黏彈性，將其作為瀝青混合料的本構模型，可用于分析瀝青混合料的蠕變特性，且結果與室內蠕變試驗結果的誤差較小。而在考慮材料的區別與外界環境的影響時，學者們對Burgers模型進行修正，得到了更貼近試驗結果的改進Burgers模型。

劉克[17]為研究瀝青混合料塑性變形積累，構建了含彈性極限σe的改進Burgers模型，不僅解決了含瞬時塑性應變改進模型的變形速率問題，也能準確計算后續加卸載過程，為瀝青混合料塑性積累變形計算提供了工具。張俊等[18]為較好描述損傷狀態下瀝青混合料的黏彈塑性應力-應變關系，建立了一個能體現瀝青混合料黏彈塑性損傷Burgers模型，通過間接拉伸疲勞試驗標定了模型參數，證明了所建模型不僅能較好描述瀝青混合料在動態循環荷載作用下的損傷本構關系，還能體現加載頻率、環境溫度及荷載水平等因素對應力-應變關系的影響。

研究人員采用Burgers模型對瀝青混合料的粘彈性進行定義，分析混合料的蠕變特性，為瀝青混合料永久變形的理論研究做出了杰出的貢獻，同時為虛擬試驗奠定了一定的基礎。但對Burgers 模型的研究多局限于進行簡單的室內試驗的擬合，部分學者對Burgers 模型進行修正與改進，著重于考慮混合料材料的區別以及外界環境因素的差異，而鮮有考慮混合料自身結構的區別。瀝青混合料為礦料、瀝青、空隙等所組成的多相復合材料，相關研究表明，瀝青混合料內部的空隙對瀝青混合料的力學性能存在較大的影響，其蠕變性能作為其中主要的影響之一[19]。在大量的科研工作中，經典的Burgers模型通常被用于表征瀝青混合料的黏彈特性，從而研究瀝青混合料的蠕變特性。對于密實型瀝青混合料而言，混合料的蠕變特性可以由經典的Burgers模型在模擬的過程中良好的表征。而對于空隙率較大的開級配瀝青混合料類型，當受到軸向壓力作用時候，混合料在發生彈塑性變形的同時，伴隨著一部分塑形變形，而經典的Burgers模型對于此類開級配瀝青混合料的蠕變特性表征結果會出現較大誤差。現基于改進的Burgers模型，通過單軸蠕變試驗獲取模型參數，用離散元法對3種空隙區別較大的瀝青混合料的黏彈性本構模型進行定義，研究混合料的蠕變特性，得到可以較好地表征空隙率較大的瀝青混合料蠕變特性的改進Burgers模型，將其作為本構模型，可為后續對于空隙率較大的瀝青混合料的力學分析提供理論基礎。

1 改進Burgers模型

1.1 模型的改進

經典的Burgers模型是由Kelvin單元的模型和Maxwell單元的模型組合而成，包含兩個彈性元件和兩個黏壺，如圖1所示。

圖1 Burgers模型

其本構方程為

(1)

式(1)中：E1、η1分別為Maxwell模型中的彈性模量及黏壺黏度；E2、η2分別為Kelvin模型中的彈性模量及黏壺黏度；σ為應力；ε為應變；t為應力作用時間。

在長期荷載作用下，不同級配類型的瀝青混合料永久變形(尤其是豎向變形)存在較大差異[20-22]。經典的Burgers模型對于密級配瀝青混合料存在較高的擬合程度，而在實驗過程中，間斷級配和開級配的軸向變形較密實型級配更大，因此，經典的Burgers模型不適用擬合所有級配瀝青混合料的永久變形。

在單軸壓縮試驗中，瀝青混合料在外部荷載作用下會出現部分塑形變形，當瀝青混合料空隙率較大時，該部分塑形變形更為明顯，且瀝青混合料空隙在混合料內部存在不確定性以及非線性，難以對其進行合理的定義，因此，就難以定義瀝青混合料在外荷載作用下的蠕變變形。基于此，在經典的Burgers模型上引入一個非線性流變元件(圖2)，用以描述瀝青混合料在軸壓過程中內部空隙的非線性變形，來表達瀝青混合料的黏彈特性。

圖2 非線性流變元件

在恒定作用力σ作用下，非線性流變元件的應變ε與時間的關系為

(2)

式(2)中：η3為非線性元件黏壺黏度；n為蠕變指數。

為了更好地表征瀝青混合料在外部荷載下的變形情況，將經典的Burgers模型與非線性流變元件的模型串聯，得到改進的Burgers模型如圖3所示。

圖3 改進的Burgers模型

改進后的Burgers模型應力應變滿足以下關系，如式(3)所示。

(3)

式(3)中：σ1、σ2為Burgers模型中的應力；σ3為非線性元件中的應力；ε1、ε2為Burgers模型中的應變；ε3為非線性元件中的應變。

利用疊加原理，得到蠕變方程為

(4)

在恒定應力σ0的作用下，改進的Burgers模型的蠕變方程為

ε(t)=J(t)σ0

(5)

式(5)中：J(t)為蠕變柔量函數，用黏彈性系數進行轉換可表示為

(6)

1.2 模型參數標定

1.2.1 試驗方法與設計

選取密級配AC-13、間斷級配SMA-13、開級配OGFC-13，級配如表1所示，分別成型3種瀝青混合料試件，每種類型的瀝青混合料分別成型3個試件，每個試件的尺寸均為：直徑100 mm，高150 mm。采用萬能試驗機MTS-10，在荷載0.2 MPa作用及25 ℃下分別對各試件進行單軸蠕變試驗。

表1 3種瀝青混合料級配

1.2.2 試驗結果分析及數據擬合

通過單軸蠕變試驗得到密級配AC-13、間斷級配SMA-13、開級配OGFC-13 3種瀝青混合料在0.2 MPa作用下的蠕變柔量，將蠕變柔量與時間的關系采用Origin軟件按蠕變方程[式(6)]進行擬合，如圖4所示。

圖4 3種混合料蠕變柔量擬合曲線

由圖4可知，3種級配類型的瀝青混合料的蠕變柔量隨加載時間呈現出相同的趨勢，即隨著時間的增長先迅速遞增，隨后在加載時間為1 000 s的時候，趨于穩定。在相同的加載時間下，不同類型瀝青混合料的蠕變柔量大小均表現為開級配OGFC-13>間斷級配SMA-13>密級配AC-13，說明密級配AC-13、間斷級配SMA-13、開級配OGFC-13瀝青混合料的抗變形的能力依次變差。在外荷載作用下的變形速率也存在一定區別。即開級配OGFC-13的變形速率大于間斷級配SMA-13，大于密級配AC-13。

1.2.3 標定模型參數

改進的Burgers模型中待定參數包括E1、E2、η1、η2、η3，根據圖4的蠕變柔量與加載時間的關系，擬合蠕變方程，得到改進的Burgers模型的擬合3種瀝青混合料的宏觀參數如表2所示。

由表2可知，改進的Burgers模型對密級配AC-13、間斷級配SMA-13、開級配OGFC-13瀝青混合料的擬合程度較高，擬合度R2均大于95%，表明改進的Burgers模型可以用于表征3種級配的瀝青混合料的黏彈性。

表2 3種類型瀝青混合料待定參數

2 改進Burgers模型合理性驗證

基于離散元法，對改進的Burgers模型的宏觀參數進行轉換，采用FISH語言編輯導入PFC3D程序中表達，進行虛擬單軸蠕變試驗，將虛擬試驗結果與室內試驗結果進行對比，探究改進Burgers模型的合理性。

2.1 離散元模型參數轉換修正

PFC3D中，經典的Burgers模型微觀模型參數難以通過試驗直接標定，現有的微觀模型參數多通過試驗宏觀參數進行轉換而得。在虛擬單軸蠕變試驗中，將不同瀝青混合料骨料球體單元間的接觸行為定義為切向和法向，相應的模型如圖5所示。微觀接觸模型參數與宏觀模型參數的換算關系如式(7)～式(14)所示。

Kmn、Cmn、Kkn、Ckn為Burgers模型的法向微觀接觸參數；Kms、Cms、Kks、Cks為Burgers模型的切向微觀接觸參數；m1、m2為相互接觸的兩球體單元

Kmn=E1L

(7)

Cmn=η1L

(8)

Kkn=E2L

(9)

Ckn=η2L

(10)

(11)

(12)

(13)

(14)

式中:L為兩球心之間的距離；ν為泊松比。

改進Burgers模型是在經典Burgers模型的基礎上添加了一個非線性元件后與Maxwell模型以及Kelvin模型串聯，二者的差別在于模型干路黏壺黏度系數的不同，為了在PFC程序中得到相應的表達，需對參數轉換過程中法向和切向的黏度參數Cmn、Cms進行修正，將非線性元件黏度系數進行疊加，計算方法如式(15)、式(16)所示，得到改進的Burgers模型的法向和切向的黏度參數Cmn、Cms。改進Burgers模型的其他微觀參數的計算方法則與經典Burgers模型相同。

Cmn=(η1+η3)L

(15)

(16)

2.2 瀝青混合料單軸壓縮試驗PFC離散元模型的建立

為了驗證改進Burgers模型對不同空隙特征瀝青混合料的黏彈性的表征效應，基于3種不同的級配(密級配AC-13、間斷級配SMA-13、開級配OGFC-13)分別建立三維虛擬模型，尺寸均為直徑100 mm，高150 mm(與室內試驗混合料試件尺寸一致)。

按照貝雷法的設計理論[23]，通過“循環”生成具有級配特征的粗集料球單元，在試件模型內填充規則排列且半徑較小的離散單元；以每個單元的球心作為中心生成六面體，對其進行隨機切割，得到不規則多面體。

為了保證模型的合理性，各球單元的體積分數與不同級配類型礦料的體積分數應保持一致。在成型的虛擬試件內部刪除一定數量的瀝青砂漿單元作為空隙結構，滿足相應的空隙要求。為了更為貼近不同類型混合料空隙率的真實情況，結合學者們對三種類瀝青混合料空隙率的研究[24-27]，最終生成空隙率為5%的密級配AC-13瀝青混合料、空隙率為12%間斷級配SMA-13瀝青混合料、空隙率為18%的開級配OGFC-13瀝青混合料，其對應的空隙特征如圖6～圖8所示。

圖6 AC-13空隙特征

圖7 SMA-13空隙特征

圖8 OGFC-13空隙特征

瀝青混合料由集料、瀝青、空隙三部分組成，在離散元模型中，各部分內部與相互之間接觸方式不同，瀝青混合料則會表現出不同的力學特性，因此需要對各單元間的接觸方式采用合理的接觸模型。在PFC5.0中，接觸的本構模型主要有剛度模型、滑動模型、粘結模型、自定義模型(Burgers模型、內聚力模型)，對不同單元之間的接觸定義模型選取如表3所示。

表3 不同單元之間的接觸模型

在接觸剛度模型中，需確定的模型參數主要有法向剛度Kn、切向剛度Ks、摩擦系數f，其中，法向剛度Kn、切向剛度Ks的計算公式分別為

Kn=4REc

(17)

式(17)中：Ec為混合料集料的宏觀彈性模量；R為球單元半徑。

(18)

結合文獻[28-29]的研究結論，Ec取55 GPa，泊松比取0.25，以此計算3種類型混合料的法向剛度和切向剛度。摩擦系數f的取值為0.35～0.5對研究結果沒有顯著影響，本文模型摩擦系數取值0.35。最后，建立的密級配AC-13瀝青混合料試件、間斷級配SMA-13瀝青混合料試件、開級配OGFC-13瀝青混合料試件三維離散元模型。

在PFC3D中，一般采用“墻”對建立的模型進行加載，而“墻”不能直接施加作用力，而通過控制其移動速度間接控制力的大小和方向來對試件進行加載。本文中，加載通過PFC3D中內置FLSH語言編寫伺服控制程序，不斷調整試件上“表面墻”的位移移動速度使軸向應力達到恒定值。

2.3 數值模擬結果與室內試驗結果的比較分析

基于上述構建的離散元模型進行虛擬試驗，采用時溫等效的計算優化方法，移位因子取104(當室內試驗加載時間為100 s時，虛擬試驗僅需加載0.01 s，計算時間大大減少)，通過“墻”施加0.2 MPa豎向荷載。同時，根據3種瀝青混合料的級配(表1)，制作3種與上述尺寸一致的瀝青混合料的圓柱體試件，在25 ℃下進行室內靜載蠕變試驗，由此得到軸向應變的值，將虛擬試驗結果和室內試驗結果繪制于同一坐標系內，如圖9所示。

圖9 試驗結果與虛擬試驗結果對比分析

由圖9可知，各級配瀝青混合料軸向應變的虛擬試驗結果與試驗結果基本一致，前20 s加載時軸向應變急劇增大，20 s之后軸向應變趨于平緩上升，上升效果不再明顯，開級配OGFC-13的軸向應變明顯大于間斷級配SMA-13，間斷級配SMA-13明顯大于密級配AC-13。

開級配OGFC-13的軸向應變的室內試驗結果與虛擬試驗結果擬合程度最好，幾乎完全一致；密級配AC-13與開級配SMA-13的室內試驗結果與虛擬試驗結果在加載1 000 s以內擬合程度較高，1 000 s以后存在較小差異。

密級配AC-13的差異較間斷級配SMA-13明顯較大，說明瀝青混合料空隙對于混合料的流變特性存在一定的影響，而改進Burgers模型可以較好地擬合空隙較大的瀝青混合料，表征其流變性能。

綜合以上，結合改進Burgers模型中非線性元件的特點，3種瀝青混合料在加載前期擬合效果均較好，不同空隙特征的瀝青混合料在加載前期均伴隨著一部分非線性變形，而空隙率較大的瀝青混合料的非線性變形更持久，因此空隙率較大的瀝青混合料虛擬試驗結果與室內試驗結果更為接近。在瀝青混合料制備過程當中，難以精確控制其空隙率的大小，結合開級配OGFC-13瀝青混合料具有大空隙率特點，其空隙率一般在15%～25%，且改進的Burgers模型與OGFC-13瀝青混合料的室內蠕變試驗結果擬合程度最高，因此確定，改進的Burgers模型在瀝青混合料空隙率大于15%時，可用于表征瀝青混合料的黏彈特性，用于其他的力學分析。

2.4 經典Burgers模型與改進Burgers模型數值模擬結果的比較分析

為了探究經典Burgers模型與改進Burgers模型在離散元中對不同類型瀝青混合料流變特性表征上的區別，將經典Burgers模型按照常規的方式進行宏觀參數擬合，再進行微觀參數轉換，將其植入PFC5.0程序中進行模擬單軸蠕變試驗，所得的軸向應變與改進Burgers模型模擬單軸蠕變試驗所得的軸向應變繪制于同一坐標系，如圖10所示。

圖10 經典Burgers模型與改進Burgers模型模擬-試驗

由圖10可知，經典Burgers模型與改進Burgers模型應用于3種類型瀝青混合料單軸蠕變試驗時，瀝青混合料試件的軸向應變趨勢與試驗結果趨于一致，前500 s的軸向應變增大較快，之后軸向應變雖然仍在繼續加大，但速率明顯減小，最終成平緩趨勢。

3種不同類型混合料經典Burgers模型的模擬結果始終在改進Burgers模型模擬結果的下方，初始加載時軸向應變差距較小，加載后期差距較大，其中，開級配OGFC-13、間斷級配SMA-13、密級配AC-13瀝青混合料的兩種模型的最終軸向應變差異以此順序由大到小，說明改進的Burgers模型在加載后期與經典的Burgers模型的差異更為明顯。

不同類型的瀝青混合料在加載前期的軸向應變并不明顯，后期存在較大差異，而空隙率越大的瀝青混合料在加載后期與試驗室結果更為接近，結合改進Burgers模型的特點，說明瀝青混合料在外荷載作用下的非線性蠕變變形更為明顯，也表明了改進Burgers模型在表征空隙率較大的瀝青混合料流變性能時的優越性。

2.5 不同溫度下改進Burgers模型的適用性

溫度是影響瀝青混合料蠕變性能的重要因素之一，為了探究改進Burgers模型對于不同空隙類型瀝青混合料在不同溫度下的蠕變特性表征狀況，分別成型5個密級配AC-13、5個間斷級配SMA-13、5個開級配OGFC-13瀝青混合料圓柱體試件，并分別在15、25、35、45、55 ℃共5個溫度梯度下進行單軸蠕變試驗。分別獲取3種瀝青混合料試件在不同溫度下的蠕變柔量與加載時間的關系，如圖11所示。采用改進Burgers模型的蠕變方程進行曲線擬合，得到相應的模型宏觀參數擬合結果如表4所示。

圖11 蠕變柔量曲線擬合

由表4可知：①3種空隙特征的瀝青混合料的擬合效果均在93%以上，擬合程度較好；②開級配OGFC-13的擬合程度高于間斷級配SMA-13，高于密實型級配AC-13；③3種混合料在溫度較高時，擬合程度更好，即溫度越高，瀝青混合料的黏彈性表現得越明顯，用改進Burgers模型表征瀝青混合料的黏彈性擬合程度越高。

表4 3種混合料在不同溫度下的宏觀模型參數

為了進一步探究改進Burgers模型在不同溫度下對3種瀝青混合料黏彈性的模擬效果，將表3中的宏觀模型參數微觀轉換，在PFC5.0中進行表達，對虛擬試件進行單軸蠕變實驗，得到虛擬試件的蠕變變形。同時，通過室內試驗得到3種混合料試件在靜載作用下不同溫度狀況的蠕變變形，虛擬試驗結果與室內試驗結果如圖12所示。

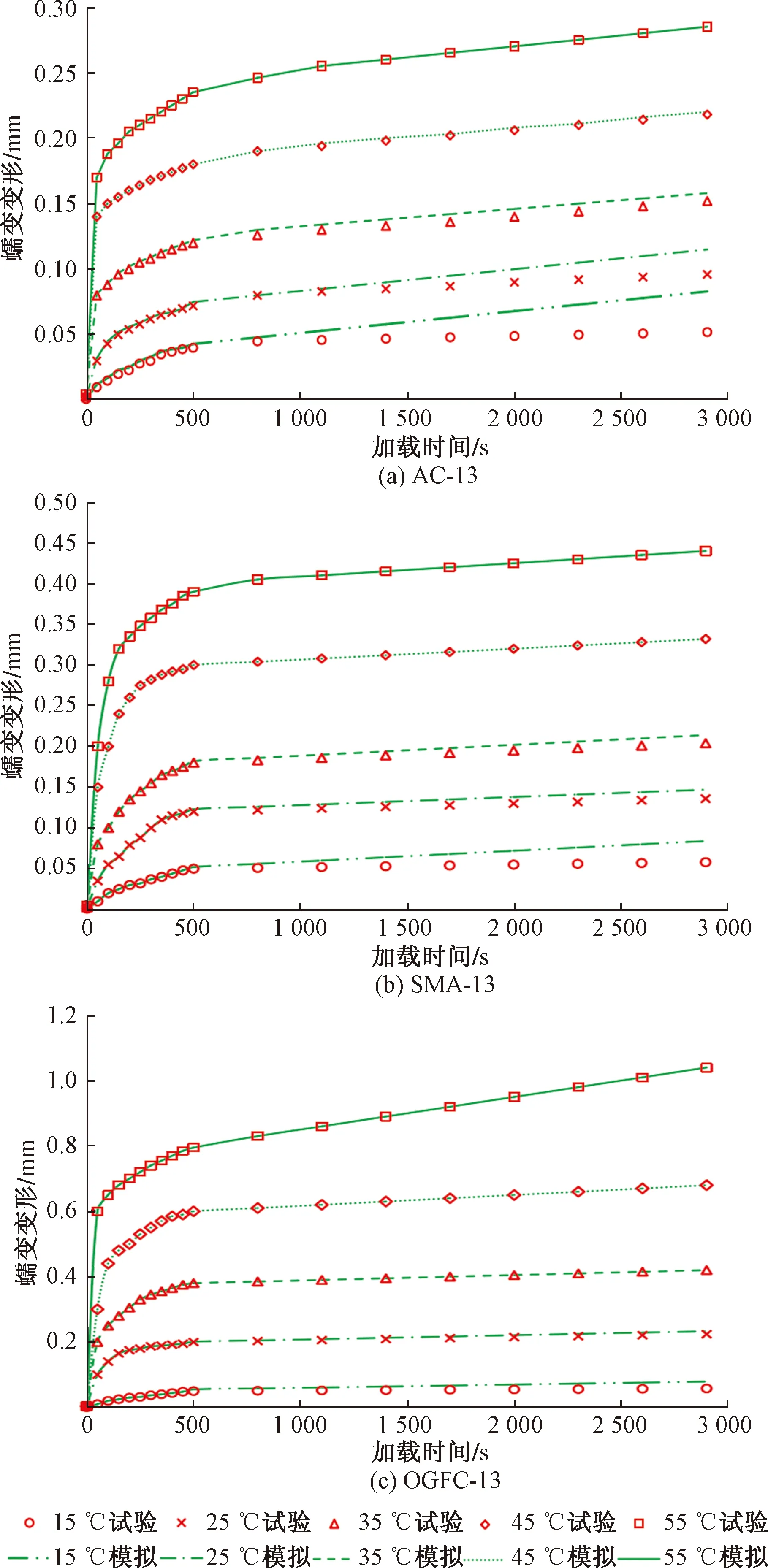
圖12 不同溫度下虛擬和室內試驗結果

由圖12可知：就密實型級配AC-13而言，采用改進的Burgers模型表征其黏彈性進行虛擬試驗，虛擬試驗結果與室內試驗結果相比，在加載前期，不同溫度下的擬合效果均較好，試驗結果與虛擬試驗結果相近，而溫度較低時，瀝青混合料偏近似與剛性，非線性階段相對不明顯，而虛實試驗基于運算表達，與室內試驗結果存在一定差異，所有在15 ℃和25 ℃的加載后期，虛擬試驗的蠕變變形量比室內試驗大，存在一定的誤差。而溫度較高時，虛擬實驗與室內試驗擬合程度較好。

對于間斷級配SMA-13，與密實型級配AC-13相似，不同溫度下加載前期的擬合程度較好，而溫度較低時，在加載后期虛擬試驗與室內試驗存在一定誤差，但誤差與AC-13瀝青混合料相比明顯較小，僅在15 ℃的環境下加載誤差較為明顯，而隨著溫度的升高，虛擬試驗的蠕變變形結果與室內試驗幾乎一致。

開級配瀝青混合料OGFC-13在試驗所采取的5個溫度梯度下的虛擬試驗結果與室內試驗結果存在較好的一致性，幾乎沒有誤差，溫度較低時，即使OGFC-13瀝青混合料偏向于剛性整體，但空隙的存在仍然會導致一部分非線性變形，而虛擬試驗結果依舊可以很好地擬合室內試驗結果，表明了改進的Burgers模型在瀝青混合料軸壓過程中非線性變形過程中的優越性。

從圖12可以看出，針對3種瀝青混合料，低溫狀態下時，瀝青硬化，使瀝青混合料具有較強的抵抗變形的能力，此時在外荷載作用下，空隙較大的瀝青混合料空隙壓縮，非線性變形更為明顯，所以在低溫狀態下時，改進的Burgers模型能夠更好地擬合空隙率較大的瀝青混合料單軸蠕變變形的試驗結果，而溫度較高時，瀝青混合料的瀝青軟化，混合料的黏彈性表達更明顯，改進的Burgers模型能較好描述3種類型瀝青混合料的黏彈特性。

3 改進Burgers模型的應用

結合改進的Burgers模型對于3種類型瀝青混合料蠕變性能的擬合結果，發現對于空隙率較大的開級配OGFC-13瀝青混合料，改進的Burgers模型的擬合程度較高。開級配OGFC-13瀝青混合料具有大空隙率特點，其空隙率一般在15%～25%，而在其制備過程當中，難以精確控制其空隙率的大小，通過室內試驗分析其蠕變性能，存在一定的難度及誤差。結合離散元PFC可以定量生成空隙率的特點，采用改進的Burgers模型定義其本構模型，分析空隙率對其蠕變性能的影響，存在一定的借鑒意義。

按照開級配OGFC-13瀝青混合料的級配(表1)成型的虛擬試件，內部刪除一定數量的瀝青砂漿單元作為空隙結構，生成空隙率為15%、17%、19%、21%、23%、25%的虛擬試件，按照25 ℃下改進的Burgers模型的宏觀參數進行微觀參數轉換，在0.1 MPa下進行虛擬單軸蠕變試驗，得到不同空隙率的虛擬試件軸向變形與加載時間的關系如圖13所示。

圖13 不同空隙率瀝青混合料蠕變特性

從圖13中可以看出，當空隙率存在差異時，相同加載條件下，瀝青混合料的蠕變特性存在明顯區別。與常規一致，虛擬試件的蠕變變形在加載前期，及加載時間在500 s以前時，軸向變形較大，在加載500 s以后，虛擬試件的蠕變變形趨于穩定。空隙率每增大2%，蠕變變形趨于平穩時的最終增量存在一定差異，具體表現為空隙率初始越大，增長相同空隙率，蠕變變形趨于平穩時的增量越大。當空隙率從23%增長到25%時，蠕變變形趨于穩定時的變形增長近1/2，且在0.1 MPa作用下，當空隙率增大10%，瀝青混合料蠕變變形趨于平穩時的增大近6倍。由此可見，空隙率對于開級配瀝青混合料OGFC-13的抗變形性能的影響較大，混合料空隙率越大，其抗變形性能越差。

4 結論

(1)修正Burgers模型可以在離散元程序中較好的表達，且能大致表征不同空隙特征的瀝青混合料的黏彈性特性，而對于空隙率較大的瀝青混合料的蠕變特性擬合效果更貼近室內試驗的實際情況。

(2)修正Burgers模型與經典Burgers模型對于瀝青混合料的黏彈性擬合效果在加載前期的區別較小，加載后期較大，同時瀝青混合料的空隙率越小，加載后期的區別越大。說明瀝青混合料的非線性蠕變變形在加載初期并不明顯，而在加載后期相對較大，且空隙率較大的瀝青混合料的非線性蠕變變形在加載過程中相對空隙率較小的瀝青混合料非線性蠕變變形更為明顯。

(3)改進的Burgers模型可較好地預測在不同溫度條件下不同空隙類型的瀝青混合料的長期蠕變變形，當溫度較低時，空隙率較大的瀝青混合料的在靜載作用下的非線性變形更為明顯，改進的Burgers模型能較好地擬合試驗結果，而溫度越高，瀝青混合料的黏彈性效果越明顯，同時改進的Burgers模型能較好描述3種類型瀝青混合料的黏彈特性。

(4)采用修正的Burgers模型研究大空隙特征瀝青混合料OGFC-13時，混合料試件的蠕變特性受空隙率的影響較大，當空隙率增大2%時，瀝青混合料蠕變變形最大可增大1/2，當空隙率增大10%時，瀝青混合料蠕變變形可增大近6倍。